b. 重庆大学 重庆市冶金工程重点实验室, 重庆 400044;
c. 重庆大学 化学化工学院, 重庆 400044
b. Chongqing Provincial Key Laboratory of Metallurgical Engineering, Chongqing University, Chongqing 400044, China;
c. School of Chemistry and Chemical Engineering, Chongqing University, Chongqing 400044, China
传统高炉炼铁技术经过3个多世纪的发展,在生产效率等方面已近乎完美,这种方法生产的铁占世界铁总产量的95%以上。传统高炉工艺主要以焦炭为燃料,而在全球炼焦煤资源匮乏和环境恶化等压力下,以更多的非炼焦煤粉为燃料的炉顶煤气循环全氧高炉炼铁技术于20世纪70年代被提出[1];全氧高炉是用常温纯氧鼓风取代传统的预热空气鼓风操作,并将炉顶煤气脱除CO2和H2O后返回高炉利用的炼铁工艺,工艺流程图见图 1。该工艺具有高喷煤量、低焦比等优越性,与传统高炉的生产效率相当[2]。随着制氧和CO2脱除等技术的逐步发展和成熟,20世纪90年代初,俄罗斯和日本分别进行了全氧高炉工业化试验[3-5]。近10年来,欧盟实施了炉顶煤气循环、无氮气高炉技术的重点开发计划,其目标是到2020年实现工业化生产[6-8]。中国煤炭资源丰富,全氧高炉有较广阔的发展空间。至今,中国学者对全氧高炉进行了诸如理论分析、模拟试验和少量工业化试验的研究[1, 9-16]。
熔融还原工艺开发等实践证明:工艺系统模拟模型在炼铁工艺革新中可发挥重要的作用,已成为工艺分析、完善流程设计、工艺系统优化的重要手段。另外,工艺系统模拟模型是炼铁生产中计算机控制系统的核心部分,进行工艺系统模拟,可为将来生产中工艺控制系统的设计奠定基础。伴随国内对传统高炉进行喷吹焦炉煤气[17]、喷吹炉顶循环煤气等的逐步展开,对此类革新技术进行工艺系统模拟研究是有必要的。国内虽已有关于全氧高炉模拟研究的报道,但因不同开发者的目的各有侧重,使已出现的模拟模型的假设、内容、模拟计算过程和方法互不相同[13, 15],其结果讨论也各有差异[1, 13, 15]。为此,笔者基于进出各反应区域的热量物料守恒原理,结合对化学反应程度和热交换程度的合理经验概括,以反应区域间的物流和能流走向关系整合计算流程,来计算物料、燃料消耗量或各种生成量,为全氧高炉的进一步开发提供信息预测服务。
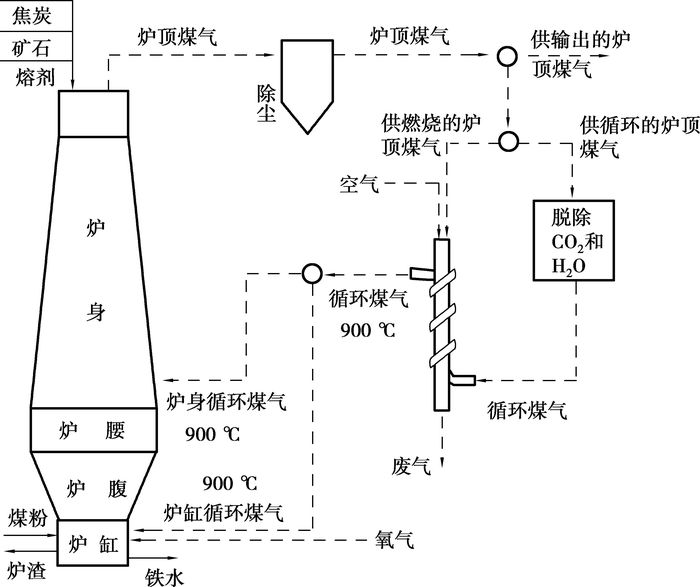
1 全氧高炉主要工艺特征全氧高炉和普通高炉的主要区别在于燃料和煤气处理系统,见图 1。其主要燃料包括煤粉和焦炭,焦炭在炉顶加入,更多煤粉由设置在炉缸中上部的风口喷入;常温氧气也由此炉缸风口吹入,同时,送入预热到900 ℃的对炉顶煤气脱除CO2和H2O后的循环煤气;为改善能量利用,另一部分预热到900 ℃的对炉顶煤气脱除CO2和H2O后的循环煤气由设置在炉身底部的风口吹入炉内。循环煤气的预热所需要的热量通过燃烧一部分炉顶煤气来提供。炉顶煤气减去供预热用的燃烧煤气和供循环的煤气后,作为外供煤气输出。
|
图 1 炉顶煤气循环全氧高炉炼铁工艺流程图 |
模拟计算时,将高炉本体分为炉身区域和炉腰、炉腹及炉缸区域两部分。主要基于两部分区域的物料、热量平衡,计算矿石、石灰石、白云石、煤、氧气的用量和各部分区域的煤气体积和成分,渣量及成分;并分析氧气炼铁工艺的煤耗、氧耗与循环煤气量等之间的关系。
高炉内发生的是多相间复杂的高温反应,要准确全面地描述此类反应较为困难,但由长期的炼铁实践可以对高炉内反应动力学的重要方面进行有效判断,具体见表 1。在工艺系统模拟模型中,不考虑各反应区域内部复杂的动力学过程,将表 1中反应物的走向、各反应区域内动力学进行的程度和损耗的数量作为经验数据在数学模型中直接使用;这样在降低模型建立难度的同时,可成功地模拟工艺过程。前述的煤气氧化度[φO(i)]的定义式为
| 表 1 炉内反应动力学的经验参数 |
| $ {\varphi _{{\rm{O}}\left( i \right)}} = \frac{{{V_{{{\rm{H}}_{\rm{2}}}{\rm{O}}\left( i \right)}} + {V_{{\rm{C}}{{\rm{O}}_{\rm{2}}}\left( i \right)}}}}{{{V_{{{\rm{H}}_{\rm{2}}}{\rm{O}}\left( i \right)}} + {V_{{\rm{C}}{{\rm{O}}_{\rm{2}}}\left( i \right)}} + {V_{{\rm{CO}}\left( i \right)}} + {V_{{{\rm{H}}_{\rm{2}}}\left( i \right)}}}}, $ | (1) |
其中,Vk(i)是i煤气中k组分的体积。炉身矿石的金属化率(Rm)定义为
| $ {R_{\rm{m}}} = \frac{{经炉身段还原后矿石中金属铁量}}{{矿石中全铁量}}。$ | (2) |
依据高炉操作经验和对全氧高炉工艺的认识,确定以下计算基准或假设:
1) 所有计算均以1 t铁水为基础,即Whotmetal=1 000 kg。
2) 由炉顶入炉的物料温度为25 ℃,入炉氧气温度为25 ℃,入炉煤粉温度为25 ℃。
3) 熔剂主要是部分煅烧的石灰石和白云石,考虑到所用铁矿石等原燃料的特点,每生产1 t铁水,硅石加入量取50 kg,即Wsilica=50 kg。
4) 煤气成分主要考虑H2、CO、CO2、H2O和N2。假设炉顶煤气中含尘量为20 g/(N·m3),炉顶煤气不低于250 ℃。同时,其氧化度[φO(topgas)]不高于0.42,入炉循环煤气温度(Tingas)为900 ℃。
出炉铁水温度(Thotmetal)为1 470 ℃,出炉渣温度(Tslag)为1 500 ℃,出炉渣中FeO的质量分数[ωFeO(slag)]为1%,MgO的质量分数[ωMgO(slag)]为12%,炉渣碱度取1.2,即
| $ \frac{{{W_{{\rm{CaO}}\left( {{\rm{slag}}} \right)}}}}{{{W_{{\rm{Si}}{{\rm{O}}_2}\left( {{\rm{slag}}} \right)}}}} = 1.2。$ | (3) |
5) 炉身区域的热损失是其热收入的2.5%,炉腰、炉腹及炉缸区域的热损失是其热收入的5%。
6) 焦比取200 kg,即Wcoke=200 kg。
2.1 计算原料用量、渣各组分的生成量进入渣中硫的质量[WS(slag)]和渣中CaS的质量[WCaS(slag)]之间的关系为
| $ {W_{{\rm{S}}\left( {{\rm{slag}}} \right)}} \times 72/32 - {W_{{\rm{CaS}}\left( {{\rm{slag}}} \right)}} = 0。$ | (4) |
渣量(Wslag)和各组分量的关系为
| $ {W_{{\rm{slag}}}} = \frac{{{W_{{\rm{CaO}}\left( {{\rm{slag}}} \right)}} + {W_{{\rm{Si}}{{\rm{O}}_2}\left( {{\rm{slag}}} \right)}} + {W_{{\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}\left( {{\rm{slag}}} \right)}} + {W_{{\rm{MnO}}\left( {{\rm{slag}}} \right)}} + {W_{{\rm{CaS}}\left( {{\rm{slag}}} \right)}} + {W_{{{\rm{P}}_2}{{\rm{O}}_5}\left( {{\rm{slag}}} \right)}}}}{{1.0 - {\omega _{{\rm{MgO}}\left( {{\rm{slag}}} \right)}} - {\omega _{{\rm{FeO}}\left( {{\rm{slag}}} \right)}}}}。$ | (5) |
文中符号Wi表示i物质的质量,i=[ore(矿石)、limestone(石灰石)、dolomite(白云石)、silica(硅石)、coal(煤粉)、coke(焦炭)、dust(炉尘)、hotmetal(铁水)、slag(炉渣)、O2(氧气)…];Wk(i)表示i物质中k组分的质量;ωk(i)表示组分k在物质i中的质量分数,k=[Fe,S,Si,P,Mn,CaO,SiO2,Al2O3,MgO,MnO,P2O5,CaS,FeO…]。
Whotmetal、Wcoke、Wsilica3个量已知;在喷煤量(Wcoal)、炉顶煤气携带粉尘量(Wdust)给定的情况下,可以利用Fe元素、P元素、S元素、CaO、SiO2、Al2O3、MgO、MnO在整个高炉内的质量守衡式、式(3)、式(4)和式(5),计算Wore、Wlimestone、Wdolomite、Wslag、WCaO(slag)、WSiO2(slag)、WAl2O3(slag)、WMnO(slag)、WCaS(slag)、WP2O5(slag)和WS(slag),11个关系式正好确定11个变量。
2.2 计算炉腰、炉腹及炉缸区域产生煤气的量在高温下,水煤气化学反应H2O+CO=H2+CO2可即刻达到平衡,其平衡常数与温度的关系式为
| $ K = \frac{{{V_{{{\rm{H}}_2}\left( {{\rm{midgas}}} \right)}} \cdot {V_{{\rm{C}}{{\rm{O}}_2}\left( {{\rm{midgas}}} \right)}}}}{{{V_{{\rm{CO}}\left( {{\rm{midgas}}} \right)}} \cdot {V_{{{\rm{H}}_2}{\rm{O}}\left( {{\rm{midgas}}} \right)}}}} = \exp \left[ {\frac{{29490 - 26.8 \times {T_{{\rm{midgas}}}}}}{{8.314 \times {T_{{\rm{midgas}}}}}}} \right]。$ | (6) |
炉腰、炉腹及炉缸区域的温度高,碳源充足,产生煤气几乎全部是还原性气体,这里假设该区域产生煤气的氧化度[φO(midgas)]为1%,即
| $ {\varphi _{{\rm{O}}\left( {{\rm{midgas}}} \right)}} = \frac{{{V_{{{\rm{H}}_2}{\rm{O}}\left( {{\rm{midgas}}} \right)}} + {V_{{\rm{C}}{{\rm{O}}_2}\left( {{\rm{midgas}}} \right)}}}}{{{V_{{{\rm{H}}_2}{\rm{O}}\left( {{\rm{midgas}}} \right)}} + {V_{{\rm{C}}{{\rm{O}}_2}\left( {{\rm{midgas}}} \right)}} + {V_{{\rm{CO}}\left( {{\rm{midgas}}} \right)}} + {V_{{{\rm{H}}_2}\left( {{\rm{midgas}}} \right)}}}} = 0.01。$ | (7) |
该区域产生的煤气,就是由高炉下部进入炉身区域的煤气。在温度(Tmidgas)给定的情况下,利用炉腰、炉腹及炉缸区域内的氢元素物质守衡式、碳元素物质守衡式、式(6)和式(7)计算该区域产生的煤气中CO、H2、CO2、H2O的体积。
炉腰、炉腹及炉缸区域产生煤气中N2的体积VN2(midgas)由氮元素物质守衡式计算。该区域产生的煤气总量为
| $ {V_{{\rm{midgas}}}} = {V_{{\rm{CO}}\left( {{\rm{midgas}}} \right)}} + {V_{{{\rm{H}}_2}\left( {{\rm{midgas}}} \right)}} + {V_{{\rm{C}}{{\rm{O}}_2}\left( {{\rm{midgas}}} \right)}} + {V_{{{\rm{H}}_2}{\rm{O}}\left( {{\rm{midgas}}} \right)}} + {V_{{{\rm{N}}_2}\left( {{\rm{midgas}}} \right)}}。$ | (8) |
文中Vi是i煤气的体积,i=[midges(炉腰、炉腹及炉缸区域产生的煤气)、topgas(炉顶煤气)、topgas1(供循环的炉顶煤气)、topgas2(供燃烧的炉顶煤气)、topgas3(供输出的炉顶煤气)、ingas(循环煤气)、ingas1(炉身循环煤气)、ingas2(炉缸循环煤气)、O2(氧气)…]。Vk(i)是i煤气中k气体组分的体积,φk(i)是i煤气中k气体组分的体积分数:
| $ {\varphi _{k\left( i \right)}} = \frac{{{V_{k\left( i \right)}}}}{{{V_{\left( i \right)}}}}, $ | (9) |
其中,k为CO、H2、CO2、H2O、N2。文中Ti是i物质的温度,i=[hotmetal、slag、midges、topgas、ingas…]。
2.3 计算炉腰、炉腹及炉缸区域需要的氧气量和煤氧气需要量(WO2)由炉腰、炉腹及炉缸区域的氧平衡求得,喷煤量(Wcoal)由炉腰、炉腹及炉缸区域的热平衡决定。
2.4 计算炉顶煤气的量和成分假设炉身区域炉料因还原而失去的氧量分别与CO、H2在还原性气体中的量成正比,则因还原炉料而产生的CO2量(VCO2, r)和因还原炉料而产生的H2O量(VH2O, r)分别为
| $ {V_{{\rm{C}}{{\rm{O}}_2},{\rm{r}}}} = {m_{\rm{O}}} \div 16 \times {R_{{\rm{CO}}}} \times 22.4, $ | (10) |
| $ {V_{{{\rm{H}}_2}O,{\rm{r}}}} = {m_{\rm{O}}} \div 16 \times {R_{{{\rm{H}}_2}}} \times 22.4, $ | (11) |
其中,RCO=[VCO(midgas)+VCO(ingas1)]÷[VCO(midgas)+VCO(ingas1)+VH2(midgas)+VH2(ingas1)];RH2=[VH2(midgas)+VH2(ingas1)]÷[VCO(midgas)+VCO(ingas1)+VH2(midgas)+VH2(ingas1)];mO为炉身区域炉料因被还原而失氧的总质量,由Wore、原料成分和给定的炉身矿石金属化率(Rm)等求出。
炉料带入炉身的H2O量(VH2O, bur)为
| $ {V_{{{\rm{H}}_2}O,{\rm{bur}}}} = \frac{{\sum\limits_i {{W_i} \cdot {\omega _{{{\rm{H}}_{\rm{2}}}{\rm{O}}\left( i \right)}}} }}{{18}} \times 22.4, $ | (12) |
式中,i=[ore、limestone、dolomite、silica、coke]。
碳酸盐分解产生的CO2量(VCO2, d)为
| $ {V_{{\rm{C}}{{\rm{O}}_2},{\rm{d}}}} = \left[ {{W_{{\rm{limestone}}}} \cdot {\omega _{{\rm{C}}{{\rm{O}}_2}\left( {{\rm{limestone}}} \right)}} + {W_{{\rm{dolomite}}}} \cdot {\omega _{{\rm{C}}{{\rm{O}}_2}\left( {{\rm{dolomite}}} \right)}}} \right] \times 22.4/44。$ | (13) |
焦炭挥发产生的CO、H2、CO2、N2的量分别为
| $ {V_{{\rm{CO,coke}}}} = {W_{{\rm{coke}}}} \cdot {\omega _{{\rm{CO}}\left( {{\rm{coke}}} \right)}} \times 22.4/28, $ | (14) |
| $ {V_{{{\rm{H}}_2}{\rm{,coke}}}} = {W_{{\rm{coke}}}} \cdot {\omega _{{{\rm{H}}_2}\left( {{\rm{coke}}} \right)}} \times 22.4/2, $ | (15) |
| $ {V_{{\rm{C}}{{\rm{O}}_2}{\rm{,coke}}}} = {W_{{\rm{coke}}}} \cdot {\omega _{{\rm{C}}{{\rm{O}}_2}\left( {{\rm{coke}}} \right)}} \times 22.4/44, $ | (16) |
| $ {V_{{{\rm{N}}_2}{\rm{,coke}}}} = {W_{{\rm{coke}}}} \cdot {\omega _{{{\rm{N}}_2}\left( {{\rm{coke}}} \right)}} \times 22.4/28。$ | (17) |
则有
| $ \begin{array}{*{20}{c}} {{V_{{\rm{topgas}}}} = {V_{{\rm{midgas}}}} + {V_{{\rm{ingasl}}}} + {V_{{{\rm{H}}_2}O,{\rm{bur}}}} + {V_{{\rm{C}}{{\rm{O}}_2}{\rm{,d}}}} + {V_{{\rm{CO,coke}}}}}\\ { + {V_{{{\rm{H}}_2}{\rm{,coke}}}} + {V_{{\rm{C}}{{\rm{O}}_2}{\rm{,coke}}}} + {V_{{{\rm{N}}_2}{\rm{,coke}}}},} \end{array} $ | (18) |
| $ {V_{{\rm{CO}}\left( {{\rm{topgas}}} \right)}} = {V_{{\rm{midgas}}}} \cdot {\varphi_{{\rm{CO}}\left( {{\rm{midgas}}} \right)}} + {V_{{\rm{ingasl}}}} \cdot {\varphi_{{\rm{CO}}\left( {{\rm{ingas}}} \right)}} - {V_{{\rm{C}}{{\rm{O}}_2}{\rm{,r}}}} + {V_{{\rm{CO,coke}}}}, $ | (19) |
| $ {V_{{{\rm{H}}_2}\left( {{\rm{topgas}}} \right)}} = {V_{{\rm{midgas}}}} \cdot {\varphi_{{{\rm{H}}_2}\left( {{\rm{midgas}}} \right)}} + {V_{{\rm{ingasl}}}} \cdot {\varphi_{{{\rm{H}}_2}\left( {{\rm{ingas}}} \right)}} - {V_{{{\rm{H}}_2}O,{\rm{r}}}} + {V_{{{\rm{H}}_2}{\rm{,coke}}}}, $ | (20) |
| $ {V_{{\rm{C}}{{\rm{O}}_2}\left( {{\rm{topgas}}} \right)}} = {V_{{\rm{midgas}}}} \cdot {\varphi _{{\rm{C}}{{\rm{O}}_2}\left( {{\rm{midgas}}} \right)}} + {V_{{\rm{ingasl}}}} \cdot {\varphi _{{\rm{C}}{{\rm{O}}_2}\left( {{\rm{ingasl}}} \right)}} + {V_{{\rm{C}}{{\rm{O}}_2}{\rm{,d}}}} + {V_{{\rm{C}}{{\rm{O}}_2}{\rm{,r}}}} + {V_{{\rm{C}}{{\rm{O}}_2}{\rm{,coke}}}}, $ | (21) |
| $ {V_{{{\rm{H}}_2}O\left( {{\rm{topgas}}} \right)}} = {V_{{\rm{midgas}}}} \cdot {\varphi _{{{\rm{H}}_2}O\left( {{\rm{midgas}}} \right)}} + {V_{{\rm{ingasl}}}} \cdot {\varphi _{{{\rm{H}}_2}O\left( {{\rm{ingasl}}} \right)}} + {V_{{{\rm{H}}_2}O,{\rm{bur}}}} + {V_{{{\rm{H}}_2}O,{\rm{r}}}}, $ | (22) |
| $ {V_{{{\rm{N}}_2}\left( {{\rm{topgas}}} \right)}} = {V_{{\rm{midgas}}}} \cdot {\varphi _{{{\rm{N}}_2}\left( {{\rm{midgas}}} \right)}} + {V_{{\rm{ingasl}}}} \cdot {\varphi _{{{\rm{N}}_2}\left( {{\rm{ingasl}}} \right)}} + {V_{{{\rm{N}}_2},{\rm{coke}}}}, $ | (23) |
其中,Vingas1是炉身需要的循环煤气量。炉顶煤气含尘量为
| $ {W_{{\rm{dust}}}} = 0.02 \times {V_{{\rm{topgas}}}}。$ | (24) |
循环煤气由炉顶煤气经脱除H2O、CO2后形成的,循环煤气各组分含量为
| $ {\varphi _{{\rm{CO}}\left( {{\rm{ingas}}} \right)}} = {\varphi _{{\rm{CO}}\left( {{\rm{topgas}}} \right)}}/\left[ {{\varphi _{{\rm{CO}}\left( {{\rm{topgas}}} \right)}} + {\varphi _{{{\rm{H}}_2}\left( {{\rm{topgas}}} \right)}} + {\varphi _{{{\rm{N}}_2}\left( {{\rm{topgas}}} \right)}}} \right], $ | (25) |
| $ {\varphi _{{{\rm{H}}_2}\left( {{\rm{ingas}}} \right)}} = {\varphi _{{{\rm{H}}_2}\left( {{\rm{topgas}}} \right)}}/\left[ {{\varphi _{{\rm{CO}}\left( {{\rm{topgas}}} \right)}} + {\varphi _{{{\rm{H}}_2}\left( {{\rm{topgas}}} \right)}} + {\varphi _{{{\rm{N}}_2}\left( {{\rm{topgas}}} \right)}}} \right], $ | (26) |
| $ {\varphi _{{\rm{C}}{{\rm{O}}_2}\left( {{\rm{ingas}}} \right)}} = 0, $ | (27) |
| $ {\varphi _{{{\rm{H}}_{\rm{2}}}{\rm{O}}\left( {{\rm{ingas}}} \right)}} = 0, $ | (28) |
| $ {\varphi _{{{\rm{N}}_2}\left( {{\rm{ingas}}} \right)}} = {\varphi _{{{\rm{N}}_2}\left( {{\rm{topgas}}} \right)}}/\left[ {{\varphi _{{\rm{CO}}\left( {{\rm{topgas}}} \right)}} + {\varphi _{{{\rm{H}}_2}\left( {{\rm{topgas}}} \right)}} + {\varphi _{{{\rm{N}}_2}\left( {{\rm{topgas}}} \right)}}} \right]。$ | (29) |
炉顶部煤气温度(Ttopgas)由炉身部分热平衡计算。
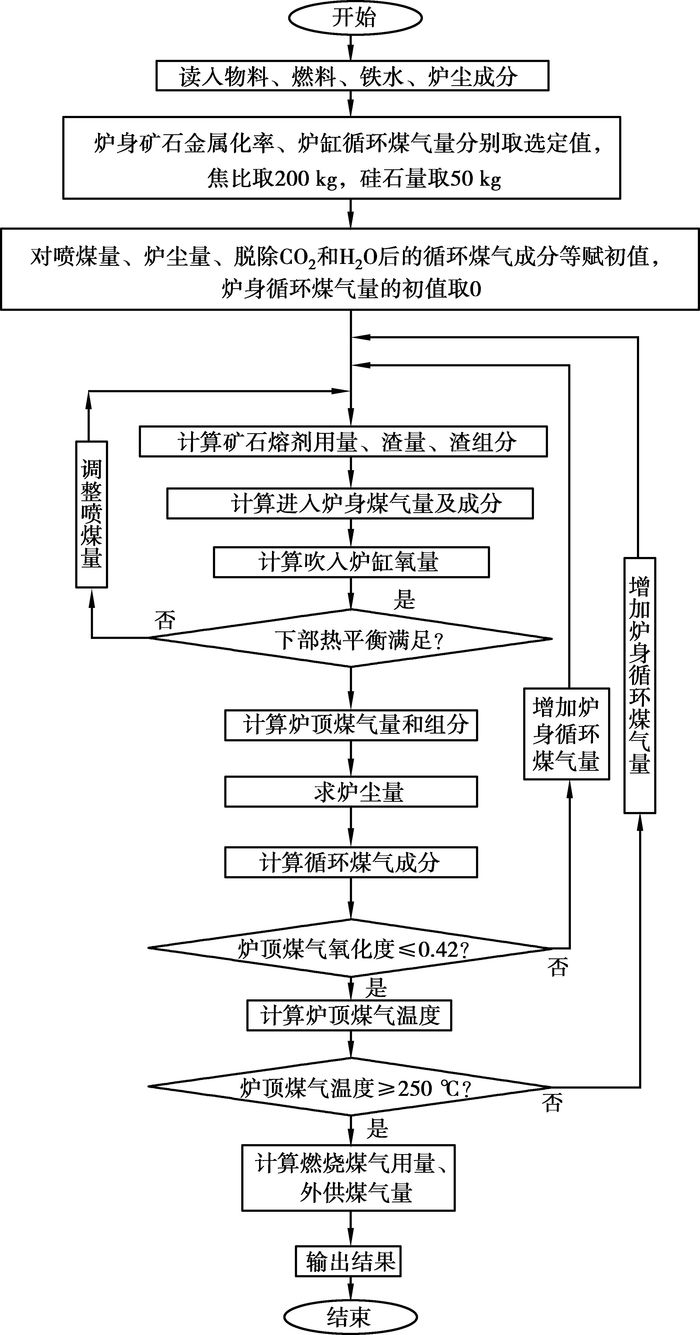
3 计算流程图以反应区域间物流和能量流走向关系确定计算方法,整个计算流程图见图 2。计算开始后,对Rm和Vingas2按计算条件赋予选定的值,对Wcoal、Vingas1、Wdust和循环煤气成分设初值,Vingas1的初值设为0。然后,计算Wore,Wlimestone,Wdolomite,Wslag,WS(slag),Wk(slag),其中,k =[CaO、SiO2、Al2O3、MnO、P2O5、CaS];计算由高炉下部进入炉身煤气的量及其成分、吹入炉缸氧量、喷煤量(反复修正喷煤量以满足炉腰、炉腹及炉缸区域的热平衡,通过迭代获得Wcoal)、炉顶煤气的量及其成分和携带炉尘量;计算循环煤气的成分。
|
图 2 计算流程图 |
在计算过程中通过逐渐增加炉身循环煤气量,以同时满足两个条件:①炉顶煤气温度不小于250 ℃;②φO(topgas)不高于0.42。大部分炉顶出来的煤气,脱除CO2和H2O后变成循环煤气在炉身和炉缸风口重新吹入炉内,以900℃吹入炉内的循环煤气又影响了炉内热和物料平衡,影响了炉顶煤气及其携带粉尘量。这样的物料走向关系,使所有待求量间任何一个参数的变化就会影响其他参数。因此,计算步骤都放在图 2所示流程图的双重调整增加Vingas1的循环体内。
同时满足炉顶煤气两个要求的计算完成后,可获得炉顶煤气的总量Vtopgas及其成分,循环煤气的成分和总量(Vingas1+Vingas2)。根据循环煤气总量可以计算出CO2和H2O脱除前供循环的炉顶煤气量(Vtopgas1)。根据热量平衡可计算出将循环煤气加热到900 ℃所需要燃烧的炉顶煤气的量(Vtopgas2)。输出系统的炉顶煤气量(Vtopgas3)为
| $ {V_{{\rm{topgas3}}}} = {V_{{\rm{topgas}}}} - {V_{{\rm{topgas1}}}} - {V_{{\rm{topgas2}}}}。$ | (30) |
若Vtopgas3>0,炉顶煤气能满足循环利用的要求,系统能匹配运行,且炉顶煤气有剩余;若Vtopgas3=0,炉顶煤气刚好满足循环使用的要求,系统能匹配运行,系统没有输出煤气;若Vtopgas3<0,炉顶煤气不能满足循环使用的要求,系统不能匹配运行。
4 模拟计算结果 4.1 原燃料、铁水和炉尘成分本模型计算所用原料成分见表 2,燃料成分见表 3和表 4,炉尘成分见表 5,铁水成分见表 6。
| 表 2 原料成分(质量分数) |
| 表 3 焦炭成分(质量分数) |
| 表 4 煤粉成分(质量分数) |
| 表 5 炉尘成分(质量分数) |
| 表 6 铁水成分(质量分数) |
在一组全氧高炉可能采用的典型工艺条件下,通过模拟计算得到的各种典型耗量和生成量见表 7;典型渣成分和总渣量见表 8;高炉下部区域产生的煤气、炉身循环煤气和炉顶煤气的典型成分及其总量见表 9。这里选用的典型工艺条件如下:焦比为200 kg,炉缸循环煤气量为300 N·m3、硅石加入量为50 kg、炉身矿石还原金属化率为90%。
| 表 7 各种单量 |
| 表 8 渣量及成分(质量分数) |
| 表 9 各种煤气量及成分 |
该典型工艺条件下,模拟计算得到的总燃料比为402.4 kg。
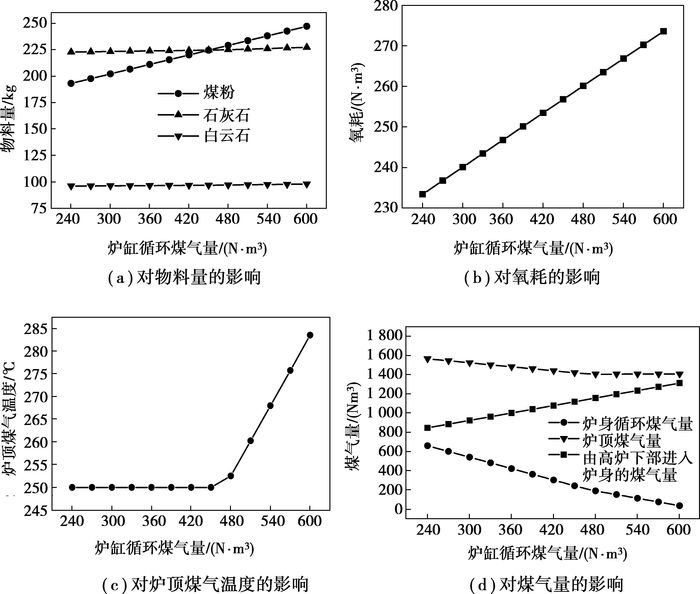
4.3 炉缸循环煤气量对全氧高炉工艺的影响循环煤气可在炉缸中上部的风口吹入,也可在炉身底部的风口吹入。炉身底部吹入循环煤气所带来的影响和炉缸吹入循环煤气的影响有较大的差别,通过模拟分析炉缸循环煤气量对全氧高炉工艺的影响是必要的。当炉缸循环煤气量在240~600 N·m3范围内变化时,计算各参数的变化规律见图 3。
|
图 3 炉缸循环煤气量对各计算量的影响 |
由图 3(a)可知:熔剂(石灰石和白云石)的耗量基本维持在一条水平直线上,即当炉缸循环煤气量逐渐增加时,它们基本不变;喷煤量的曲线有一定的斜率,当炉缸循环煤气量增加,煤耗增加较明显。煤耗增加原因之一是随炉缸循环煤气量增加,有更多的热量被煤气从高炉下部区域带入到炉身;由于煤耗的增加,煤带入的灰分增多,产生的总渣量增多,渣带去的热量增多,这是煤耗有较明显变化的另一原因。除了铁水渗碳、矿石还原的碳消耗外,其他的碳元素基本均与吹入炉内的氧反应。因此,当煤量随炉缸循环煤气量增加时,吹氧量也随之增加,如图 3(b)所示。
煤耗和氧耗随炉缸循环煤气量基本线性增加的,但炉顶煤气温度、炉顶煤气量、炉身循环煤气量随之变化出现了拐点。图 3(c)示出:炉缸循环煤气量在450 N·m3之前,炉顶煤气温度维持在250 ℃不变,之后,煤气温度逐渐增加。图 3(d)示出:在同样位置之前,炉顶煤气量和炉身循环煤气量随炉缸循环煤气量变化较快,之后,此两种煤气量随炉缸循环煤气量的变化变慢。炉顶煤气温度、炉顶煤气量和炉身循环煤气量是按照炉身区域的物料和热量平衡计算的。在拐点(炉缸循环煤气量为450 N·m3)之前,在总循环煤气中,炉身循环煤气占的比重较大,而循环煤气的入炉温度只有900 ℃,单位体积炉身循环煤气所含显热较少,当进入炉身的煤气带来的热量满足了炉顶煤气温度为250 ℃的要求时,煤气中还原性气体已达φO(topgas)<0.42;拐点之后,在总循环煤气中,炉缸循环煤气占的比重较大,炉缸循环煤气经过炉缸、炉腹及炉腰区域后,再进入炉身区域,进入炉身时煤气温度高于1 100℃,这时的煤气在单位体积内所含显热较多,当进入炉身的煤气中还原性气体满足了φO(topgas)=0.42要求时,这些煤气带来的热量已使炉顶煤气温度大于250 ℃。图 3(c)、(d)中炉顶煤气温度和煤气量等随炉缸循环煤气的变化现象,反映了炉身喷吹循环煤气和炉缸喷吹循环煤气的区别。
当炉缸循环煤气量在240~600 N·m3变化时,计算的高炉下部产生的煤气、炉顶煤气的成分具体值分别见表 10、表 11。煤气主要来源于煤粉、焦炭和氧气的燃烧,尽管随炉缸循环煤气量的增加,喷煤量和氧耗增加较明显,但由表 10、表 11看出它们对煤气成分影响不太明显。
| 表 10 由高炉下部进入炉身的煤气成分 |
| 表 11 炉顶煤气成分 |
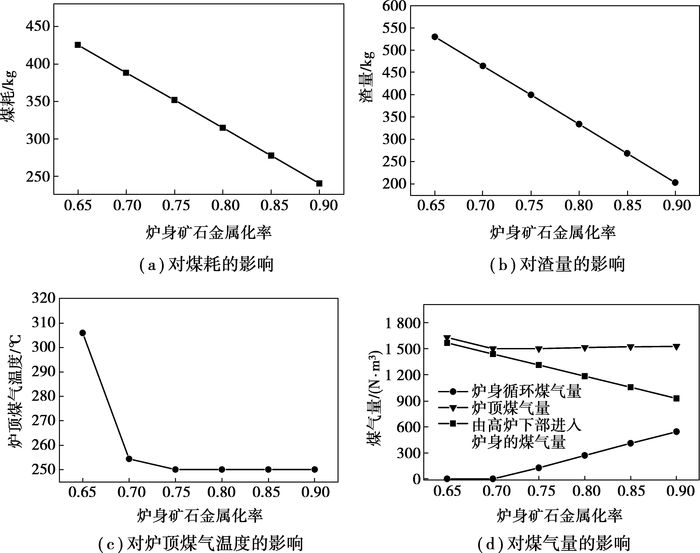
传统炼铁高炉中,增加间接还原度,降低直接还原度,可降低焦比和燃料比。矿石在炉身的还原程度影响系统的能耗。现分析炉身矿石金属化率对全氧高炉工艺的影响。当矿石金属化率在0.65~0.90范围内变化时,计算的结果见图 4。
|
图 4 炉身矿石金属化率对各计算量的影响 |
图 4(a)示出炉身矿石金属化率增加时喷煤量明显降低,这与传统高炉的提高间接还原度可降低燃料比的原因是一致的。因矿石还原、熔化分离需要必要的热量,发展间接还原也需要足量的煤气量,所以,当消耗的燃料不足以提供熔炼所需要的热量或不足以满足间接还原所需要的煤气量时,就不能一直靠减少直接还原以降低燃料消耗。炉身矿石金属化率的增加是有限度的;当焦比为200 kg,炉缸循环煤气量为300 N·m3、硅石加入量为50 kg时,通过计算表明炉身矿石金属化率超过93%时,总的燃料消耗不足以提供完成正常冶炼所需要热量或煤气量。煤粉消耗的降低,煤粉带入的灰分减少,产生的总渣量随炉身矿石金属化率的增加而减少,如图 4(b)所示。
当炉身矿石金属化率较低时,如图 4(c)中的0.65~0.70,煤耗大,高炉下部产生的煤气量多,且它的温度比循环煤气的入炉温度(900 ℃)高很多,这时炉身风口不用再吹入循环煤气(如图 4(d)所示),炉顶煤气温度就可超过250 ℃,同时满足氧化度小于0.42的要求。当炉身矿石金属化率较高[如图 4(c)中的0.75~0.90]时,煤耗小,高炉下部产生的煤气量少,这时炉身风口需吹入循环煤气,金属化率越大,Vmidgas越小,Vingas1越大;单位体积炉身循环煤气所含显热较少,当进入炉身的煤气带来的热量满足了炉顶煤气温度为250 ℃要求时,煤气中还原性气体已使φO(topgas)<0.42。
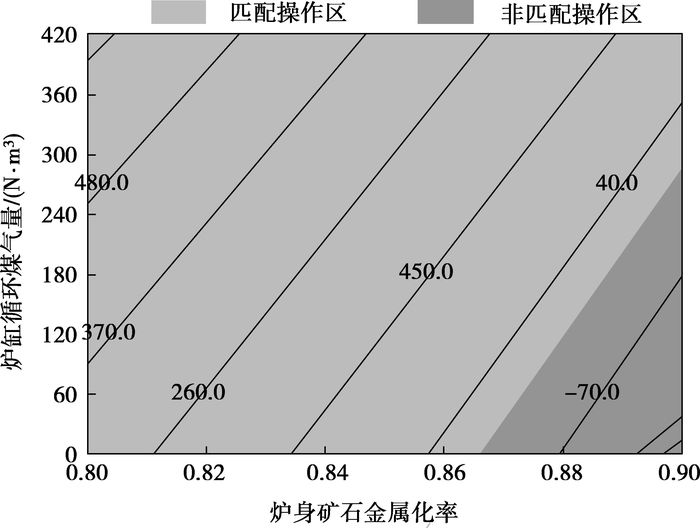
4.5 煤耗与系统输出煤气量的关系图 5用计算出的输出煤气量(Vtopgas3)的等值线图反映它在一定范围内随炉身矿石金属化率、炉缸循环煤气量的变化。当炉身矿石金属化率过低时,矿石靠直接还原的比例大,能耗大,炉顶煤气温度升高,能量利用率低;当其过高时,矿石还原主要靠间接还原,在高温区产生的煤气量不足以满足间接还原的需求;当炉缸循环煤气量过大时,由下部带入炉身的热量过多,煤耗大,炉顶煤气温度升高,能量利用率也低。因此,图 5中炉身矿石金属化率变化范围取0.80~0.90,炉缸循环煤气量范围取0~420 N·m3。图中红色区域是系统不能匹配操作的区域(Vtopgas3<0);绿色区域是系统能匹配操作的区域(Vtopgas3>0)。图 5示出:在系统匹配操作区内,Vtopgas3的等值线基本上可看做直线。每条等值线上各点对应的能耗,以及能耗和输出煤气量的关系见图 6。
|
图 5 操作参数对系统匹配操作的影响 |
|
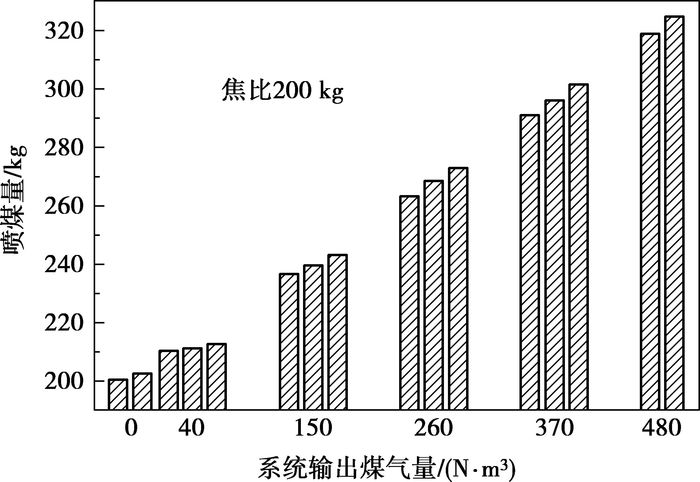
图 6 系统输出煤气量和煤耗的关系 |
图 6中,每一个输出煤气量的值对应2~3个煤耗值,其中Vtopgas3=0或480 N·m3对应的2个煤耗值是按图 5中相应输出煤气量等值线上相距足够远的两点所对应的操作参数Vingas2和Rm计算而得到的;3个煤耗值是按图 5中相应输出煤气量等值线上相距足够远的两点和此两点的中点所对应的操作参数计算而得到的。由图可见,在每一条输出煤气量的等值线上,相距足够远的两点对应的煤耗相差不大,中点对应的煤耗值居于此两点对应煤耗值之间。因此,在图 5的任一条输出煤气量等值线上,任何两点对应的煤耗值相差应该都不大。Vtopgas3 =0等值线上各点对应的煤耗的计算值基本维持在200 kg,Vtopgas3 =40.0 N·m3等值线上各点对应的煤耗的计算值基本维持在212 kg,Vtopgas3 =150.0等值线上各点对应的煤耗的计算值基本维持在240 kg。从图 6能清楚地看出煤耗和系统输出煤气量的关系,煤耗基本随系统输出煤气量的增加而线性增加。
要使系统维持在最低的能耗水平,可通过操作使炉缸循环煤气量和炉身矿石金属化率的值位于图 5中匹配区和非匹配区的交界线上,若将图 5中等值线近似处理成直线,可获得能耗最低时Vingas2和Rm近似满足的关系式:
| $ {V_{{\rm{ingas2}}}} = - 7224.55 + 8348.26 \times {R_{\rm{m}}}, $ | (31) |
其中,炉身矿石金属化率可在由图 5查得的0.866<Rm<0.9的范围内取值。按此范围和式(31)确定的参数来操作,炉顶煤气能满足返回利用的要求,且没有剩余。同样地,要使系统输出煤气量维持260 N·m3,可使炉身矿石金属化率在0.811<Rm<0.868范围内取值,炉缸循环煤气量按Vingas2=-6 025.77+7 430.59×Rm关系确定,这时煤耗维持在270 kg左右,炉顶煤气返回利用后,还有260 N·m3剩余。
5 结论1) 以长期工艺实践为基础,对全氧高炉内各区域的化学反应和热交换程度以合适参数概括;以物料和热量守衡原理为基础分别对炉腰、炉腹及炉缸区域和炉身区域进行单元模化;以区域间物料和热量流向关系进行各区域的计算衔接,形成对全氧高炉工艺的系统模拟。该系统模拟模型能够计算不同原燃料、不同操作参数下的原料消耗、熔剂消耗、渣量及其成分、各种煤气量及其成分,还可以分析燃料消耗和炉身还原程度、循环煤气量等工艺参数的关系。
2) 在给定原燃料条件下,当焦比为200 kg,炉缸循环煤气量为300 N·m3,硅石加入量为50 kg,炉身矿石还原金属化率为90%时,模型预测得出如下结果:石灰石耗量、白云石耗量、喷煤量、氧耗、渣量、炉身循环煤气、炉顶煤气分别为223.6,96.6,202.4,240.2,370.3,543.4,1 525.97 N·m3。
3) 模型计算结果表明:在炉身矿石金属化率为90%时,若以炉身底部风口吹入较多的循环煤气,热量的需求决定了炉身内还原所需的煤气量;若以炉缸风口吹入较多的循环煤气,还原性气体的需求决定了炉身内还原所需的煤气量。
4) 当焦比为200 kg,炉身矿石金属化率为0.80~0.90,炉缸循环煤气量在0~420 N·m3范围操作时,煤耗基本随系统输出煤气量的增加而线性增加;在相同系统输出煤气量(煤耗)约束下,炉身矿石金属化率Rm有更具体的取值范围,且炉缸循环煤气量Vingas2与其近似满足线性关系,如在最低煤耗(系统输出煤气量为0)时,0.866<Rm<0.9,且Vingas2和Rm满足的关系为:Vingas2=-7 224.55+8 348.26×Rm。
| [1] |
高建军, 郭培民, 齐渊洪, 等.
工艺参数对氧气高炉能耗的影响规律[J]. 钢铁研究学报, 2011, 23(7): 14–17.
GAO Jianjun, GUO Peimin, QI Yuanhong, et al. Effect of process parameters on energy consumption of the oxygen blast furnace[J]. Journal of Iron and Steel Research, 2011, 23(7): 14–17. (in Chinese) |
| [2] | 张建良. 氧气高炉的应用基础研究[D]. 北京: 北京科技大学, 2001. |
| [3] | Tesitlin M A, Lazutkin S E, Styopin G M. A flow-chart for iron making on the basis of 100% usage of process oxygen and hot reducing gases injection[J]. ISIJ International, 1994, 34(7): 570–573. DOI:10.2355/isijinternational.34.570 |
| [4] | Ohno Y, Hotta H, Matsuura M, et al. Development of oxygen blast Furnace process with preheating gas injection into upper shaft[J]. Tetsu-to-Hagane, 1989, 75(8): 1278–1285. DOI:10.2355/tetsutohagane1955.75.8_1278 |
| [5] | Yamaoka H, Kamei Y. Experimental study on an oxygen blast furnace process using a small test plant[J]. ISIJ International, 1992, 32(6): 709–715. DOI:10.2355/isijinternational.32.709 |
| [6] |
徐匡迪.
低碳经济与钢铁工业[J]. 钢铁, 2010, 45(3): 1–12.
XU Kuangdi. Low carbon economy and iron and steel industry[J]. Iron and Steel, 2010, 45(3): 1–12. (in Chinese) |
| [7] | Danloy G, Berthelemot A, Grant M, et al. UlCOS:pilot testing of the low-co2 blast furnace process at the experimental BF in Lulea[J]. Rev. Metal.Paris, 2009, 106(1): 1–8. DOI:10.1051/metal/2009008 |
| [8] | Zuo G Q, Hirsch A. The trial of the top gas recycling blast furnace at lkab's ebf and scale-up[J]. Metallurgical Research & Technology, 2009, 106(9): 387–392. |
| [9] |
秦民生, 高征铠, 王冠伦.
高炉全氧鼓风操作的研究[J]. 钢铁, 1987, 22(12): 1–7.
QIN Minsheng, GAO Zhengkai, WANG Guanlun. Study on blast furnace ope ration with all oxygen blast[J]. Iron and Steel, 1987, 22(12): 1–7. (in Chinese) |
| [10] | Qin M S, Gao Z Ki, Wang G L, et al. Blast furnace operation with full oxygen blast[J]. Ironmaking and Steelmaking, 1988, 15(6): 287–292. |
| [11] |
高征铠, SommervilleI D.
氧气煤粉熔剂复合喷吹(OCF)高炉炼铁工艺的研究[J]. 钢铁, 1994, 29(6): 13–18.
GAO Zhengkai, Sommerville I D. Study on OCF blast furnace process[J]. Iron and Steel, 1994, 29(6): 13–18. (in Chinese) |
| [12] |
尹建威, 王凤岐, 党玉华, 等.
氧气高炉炉身的模拟试验研究[J]. 钢铁研究学报, 2002, 14(2): 1–4.
YIN Jianwei, WANG Fengqi, DANG Yuhua, et al. Experimental simulation on reduction process of shaft for oxygen blast furnace[J]. Journal of Iron and Steel Research, 2002, 14(2): 1–4. (in Chinese) |
| [13] |
韩毅华, 王静松, 李燕珍, 等.
炉顶煤气循环氧气鼓风高炉综合数学模型[J]. 北京科技大学学报, 2011, 33(10): 1280–1286.
HAN Yihua, WANG Jingsong, LI Yanzhen, et al. Comprehensive mathematical model of top gas recycling-oxygen blast furnaces[J]. Journal of University of Science and Technology Beijing, 2011, 33(10): 1280–1286. (in Chinese) |
| [14] |
齐渊洪, 严定鎏, 高建军, 等.
氧气高炉工业化试验研究[J]. 钢铁, 2011, 46(3): 6–8.
QI Yuanhong, YAN Dingliu, GAO Jianjun, et al. Study on industrial test of the oxygen blast furnace[J]. Iron and Steel, 2011, 46(3): 6–8. (in Chinese) |
| [15] |
郭培民, 高建军, 赵沛.
氧气高炉多区域约束性数学模型[J]. 北京科技大学学报, 2011, 33(3): 334–338.
GUO Peimin, GAO Jianjun, ZHAO Pei. Multi-zone constrained mathematical model of oxygen blast furnace[J]. Journal of University of Science and Technology Beijing, 2011, 33(3): 334–338. (in Chinese) |
| [16] |
高建军, 齐渊洪, 周渝生, 等.
氧气高炉炼铁技术分析[J]. 钢铁钒钛, 2012, 33(2): 40–45.
GAO Jianjun, QI Yuanhong, ZHOU Yusheng, et al. Technical analysis on oxygen blast furnace ironmaking process[J]. Iron Steel Vanadium Titanium, 2012, 33(2): 40–45. DOI:10.7513/j.issn.1004-7638.2012.02.008 (in Chinese) |
| [17] |
周亮, 刘克明, 沙永志.
高炉喷吹焦炉煤气置换比的计算[J]. 钢铁研究学报, 2013, 25(5): 19–23.
ZHOU Liang, LIU Keming, SHA Yongzhi. Calculation of replacement ratio of injecting coke oven gas into blast furnace[J]. Journal of Iron and Steel Research, 2013, 25(5): 19–23. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

