在目前的港工结构中,钢筋混凝土已经成为非常重要的组成部分,被广泛地用在国内外众多跨海大桥的桥墩上。但是在长期海洋环境的情况下,结构会受到不可逆转的破坏。这种破坏在世界范围内带来了巨大的经济损失[1]。因此,钢筋混凝土结构的耐久性问题引起了广大学者的重视。
腐蚀疲劳的概念最早是在20世纪初期被Haigh教授提出的,之后的EvansV.R.通过长期的工程试验,认为腐蚀疲劳是一个值得重视的问题。关于混凝土的破坏状态,Bazant运用电化学的知识,提出了关于钢筋破坏形态的2种假设:平行钢筋层面的开裂和保护层顺筋开裂。但是他并没有提出理论上的依据。惠云玲通过实验分析,得到了锈蚀量与其他相关因素之间的公式。他们都是通过实验找到锈蚀量与影响速度之间的关系。张伟平等通过研究发现,腐蚀率与钢筋的函数关系存在一定的差异[2]。李颖研究了混凝土结构的腐蚀疲劳性能,并且运用ANSYS软件对混凝土柱配箍率对裂缝的影响进行了分析[3]。
对于破坏形态,前人没有从理论上给出分析,而且在做实验的时候,没有考虑到疲劳强度的影响,没有系统地提出破坏的过程。对于钢筋锈蚀量的评估,由于所采用的研究方法各不相同,并且该问题比较复杂,评估的方式也不一样。对于可靠度的研究,未见到相关计算方法的报道。
文中分析了钢筋混凝土结构从最开始的锈蚀到结构开裂的过程,以及在这个过程中钢筋所发生的一系列变化,对每一个阶段都给出了详细的理论和实际分析。其次,对锈蚀量评估的几种方法进行了具体的比较。最后分析氯离子在混凝土中扩散的过程,建立混凝土中氯离子浓度分布的随机模型,得到氯离子浓度的均值和方差。运用可靠度的相关理论,对钢筋混凝土构件进行了耐久性评估。
1 钢筋混凝土结构的锈裂破坏形态 1.1 混凝土碳化水泥在遇到水的时候,其中的氧化钙会生成氢氧化钙以及其他碱性化合物。一部分会溶解于孔溶液中,剩下的绝大部分仍然以固态的形式与水泥的浆体结合在一起[4]。
钢筋混凝土的表面有电位差,不同电位之间形成了阳极和阴极;
阴极有水分和氧气,发生阴极反应:O2+2H2O+4e-4OH-
处于阳极的钢筋表面能够发生以下反应:2Fe-4e-4OH-
在一段时间之后,氢氧化铁中的一部分会被进一步氧化成nFe2O3·mH2O(红锈),另一部分生成Fe3O4(黑锈),红锈的体积可以扩大到4倍,黑锈的体积增大到原来的2倍,在钢筋混凝土的表面生成一层铁锈,铁锈的体积持续增大会对附近的混凝土产生一定程度的压力,导致混凝土钢筋顺筋的方向开裂,钢筋开裂会导致保护层成片的脱落,致使钢筋发生更剧烈的锈蚀。
1.2 氯离子侵蚀在海洋环境下,钢筋混凝土结构与海水接触,海水中含有大量的氯离子,氯离子具有非常强的穿透能力,即使混凝土没有被碳化,氯离子通过扩散或者毛孔的吸附进入到混凝土内部的钢筋表面。当接触到钢筋表面的钝化膜时,可使钝化膜处的酸碱值成强酸性。
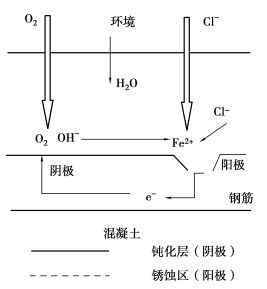
氯离子对钢筋的锈蚀作用,Zhang[5]通过对2根已在自然的氯盐环境中被腐蚀了十几年的梁进行研究。氯离子造成的钢筋锈蚀可以看作是电池反应,由于混凝土不均匀,使得氯离子首先对钢筋表面的局部点进行破坏,这些地方露出铁,形成阳极,而钢筋表面大部分的钝化膜则形成阴极。阴阳极之间发生电池反锈蚀过程如图 1所示。
|
图 1 氯离子锈蚀的机理 |
如果混凝土钢中存在大量的氯离子,并且钝化层比较薄,充足的氧气可以达到钢筋的表面,钢筋上就可以大面积的发生上述的氯离子去钝化反应,点蚀的面积扩大并且不断合并,造成大面积的锈蚀。氯离子在整个过程中没有被消耗掉,所以只要是进入混凝土中的氯离子都可以被反复的使用,起到破坏作用。
2 钢筋锈裂的发展过程钢筋锈裂的过程大致有2个阶段:钢筋锈蚀阶段和锈蚀开裂损坏阶段。
2.1 钢筋锈蚀阶段在这个阶段中,混凝土中的钢筋通过预备阶段和发展阶段最终形成锈蚀。从混凝土刚开始被使用到混凝土中的钢筋被氯离子侵入而导致钝化膜损坏,也就是到钢筋刚开始产生锈蚀现象的时候结束,这段时间用t0表示,把这个阶段称作预备阶段,也就是前期。而从钢筋最开始被氯离子侵蚀到钢筋大面积被侵蚀以至于钢筋结构不能够再使用为止,这段时间成为发展阶段。又可以将发展阶段分为中期、后期、晚期。中期指的是从钢筋开始发生锈蚀到钢筋因锈蚀发生膨胀而导致混凝土表面出现明显的破坏现象,如混凝土剥落、顺筋胀裂、混凝土层裂等,中期的时间用t1表示。后期指的是中期到混凝土发生严重的剥落损坏及严重胀裂,此时必须要进行大面积的修补,这个时间段用t2。从后期开始到钢筋的锈蚀扩大到结构里面导致结构里面严重破坏以至于不能够使用的这段时间称为晚期,用t3表示。
对于绝大多数普通钢筋混凝土结构而言,t3<t2<t1<t0,设计的使用寿命选取为t0+t1+t2=t,要想进行修补并且取得良好的效果,最好是在t0时间之内,最晚应该在t1时间段内。
2.2 锈蚀开裂破坏钢筋锈蚀发展到晚期的时候会导致钢筋开裂,这个过程分为以下4个阶段。
2.2.1 膨胀阶段氯离子接触到钢筋表面,破坏钝化膜的时候,位于阳极的二价铁离子会被氧化成为三价铁离子,Fe3+与OH-发生化学反应形成Fe(OH)3。钢筋发生锈蚀的时候,生成的锈蚀产物会不断的填充钢筋与混凝土接触之间的细微孔隙。如果钢筋的锈蚀量不足以填充孔隙,那么在钢筋混凝土结构中就不会有任何的应力。
2.2.2 产生应力阶段如果钢筋发生锈蚀的量超过了孔隙被填满所需要的量时,那么会对周边的混凝土造成膨胀的压力,并且这种压力与钢筋的锈蚀量成正比。影响孔隙的因子通常与混凝土硬化时的收缩量和混凝土浇捣的质量有关系,当水泥的量加大,混凝土的密度减小,灰水比减小的时候孔隙增大。而钢筋所产生的锈蚀量跟锈蚀产物的成分还有锈蚀的速度有着密切的关系。
2.2.3 产生裂纹阶段对于钢筋锈蚀导致混凝土的保护层开裂这个问题,很多学者[6-7]进行了试验研究。当钢筋的锈蚀量累积到大量的时候,会在混凝土中产生一定的力,而当混凝土内部的强度不能够承受由锈蚀量所带来的力时,发生锈蚀的部分会产生裂纹。钝化层开裂的时候钢筋中产生锈蚀的量被称作临界锈蚀量。
临界锈蚀量与钢筋锈蚀量同时决定了裂纹的产生。临界锈蚀量与钝化层的厚度还有钢筋混凝土的质量有关。如果混凝土的强度高且钝化层的厚度比较大,那么钢筋的临界锈蚀量也比较大,反之,混凝土的强度较低且钝化层的厚度较小的话,临界锈蚀量也比较小。
2.2.4 裂缝扩大阶段当钢筋锈蚀量超过临界量的时候,钢筋的锈蚀会顺着这些裂缝一直到钢筋的表面,如果此时不采取维护措施,那么钢筋的锈蚀会一直发展直至钝化层脱落。Cherni[7]将混凝土保护层划为内裂和外裂2个区域。对于混凝土裂缝的观察,可以采用Chermin L等的方法[8],将应变片贴到混凝土上,应变值的大小间接反映了裂缝的大小。
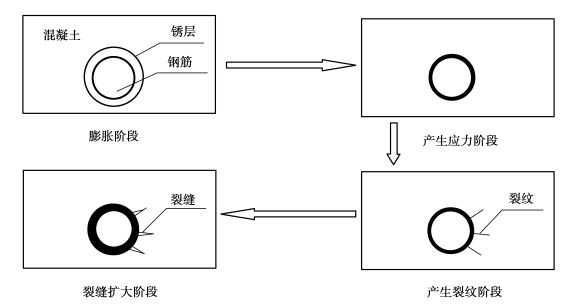
钢筋因锈蚀发生开裂的过程可用图 2表示。
|
图 2 钢筋锈裂的过程 |
钢筋的锈蚀量对衡量钢筋混凝土结构的性能优劣具有重要的作用,因此,在对钢筋混凝土结构进行锈裂损伤评估的时候,钢筋锈蚀量的评估是最基本的工作。对于钢筋锈蚀量的评估,很多学者都进行了试验研究[9-11],通过记录出现裂缝时代通电时间而记录,这种方法得到的锈蚀量与真正的锈蚀量之间存在着差异。
在海洋环境下,钢筋混凝土最先发生局部的点锈(坑锈),点锈的发展速度非常快,并且要比均匀的锈蚀更加危险。在对点锈进行评估的时候应该注意以下几个方面:1)锈蚀的坑的大小;2)坑的深度;3)坑的面积。通常用以下2种模型对钢筋的锈蚀量进行评估:一是工程模型。这个模型中,让混凝土单位面积上锈蚀的点数的规律与泊松分布相同;二是电化学诊断方法。这个方法是日本学者提出来的,用测量仪器记录下钢筋的电位、混凝土的电阻、极化电阻,并且用微机将测量出来的3个要素的值进行换算,使之成为能够进行评价的数值,将锈蚀的程度分为3个等级:未锈蚀,轻度锈蚀,严重锈蚀,这3个等级用不同的颜色表示。从理论上来讲,第1种方法比较合理,但该方法中缺少具体的参数和关于锈蚀量的计算公式。而电化学三要素对钢筋锈蚀进行诊断的方法,精度上虽然高于传统的方法,而且评价软件也已经开发成熟进入实用阶段,但是此方法只是根据钢筋的锈蚀程度进行了分级,缺少具体的数值。
当混凝土中的钢筋锈蚀发展的较为严重的时候,混凝土会发生开裂,钢筋会暴露出来,一旦与海水接触,钢筋的锈蚀速度就加快了,使得混凝土与钢筋之间更为松散。在这种情况下,临界锈蚀量是一个非常重要的因素。通过实验法、力学模型分析法和有限元法对临界锈蚀量进行评估。而实验中得到的钢筋临界锈蚀量的评估公式,是在钢筋锈蚀均匀的情况下进行的,它的适用性范围比较小。
4 海洋环境下钢筋混凝土可靠度 4.1 建立被锈蚀钢筋的截面积模型在海洋的腐蚀环境下,钢筋由于宏电流的出现产生非均匀的锈蚀,对于这种点蚀不能用均匀锈蚀的相关指标来衡量横截面的变化。Kim[12]基于弹性力学理论对钢筋混凝土结构的锈裂过程进行了研究,假定锈蚀是均匀的,而Malumbela[13]认识到了锈蚀的不均匀性,在这个条件下,建立了钢筋锈蚀情况与混凝土的裂缝之间的关系模型。
用icorr(tp)表示锈蚀开始tp时间后的电流密度(μA/cm2),根据工程的实际测量得到
| $ {i_{{\rm{corr}}}}\left( {{t_p}} \right) = 32.13t_{\rm{p}}^{ - 0.29}\frac{{{{\left( {1 - C/W} \right)}^{ - 1.64}}}}{c}, $ | (1) |
其中:c为混凝土保护层的厚度,cm;C/W为灰水比。
钢筋的锈蚀率:λ=0.0116icorr(tp)。
由此可以得到在钢筋结构使用t时刻的时候,钢筋的横截面积A(t)为
| $ \left. \begin{array}{l} A\left( t \right) = \frac{{{\rm{ \mathsf{ π} }}n}}{4}{\left[ {{\rm{d}}\left( t \right)} \right]^2},t > {t_{{\mathop{\rm int}} }};\\ A\left( t \right) = \frac{{{\rm{ \mathsf{ π} }}n}}{4}{\rm{d}}_0^2,t \le {t_{{\mathop{\rm int}} }}。\end{array} \right\} $ | (2) |
其中tint表示钢筋开始发生锈蚀的时间,a;d(t)表示t时刻时锈蚀的钢筋的直径,mm;d0表示还未锈蚀的钢筋的直径,mm:d0=d(t)+0.0232
根据费克(Fick)第二扩散定律,在混凝土比较潮湿的条件下,混凝土中氯离子中的渗透过程符合以下规律[14]:
| $ \frac{{{D_C}{\partial ^2}C\left( {x,t} \right)}}{{\partial {x^2}}} = \frac{{\partial C\left( {x,t} \right)}}{{\partial t}}。$ |
在海洋环境下,风中携带的氯离子将聚集在混凝土的表面,这些氯离子的浓度会随着时间而增大。Mullard和Stwart给出了在t时刻混凝土表面以下x处的氯离子浓度计算公式:
| $ 2W\left[ {\exp {{\left[ { - \frac{{{x^2}}}{{4D}}} \right]}_t}\sqrt {\frac{t}{{{\rm{ \mathsf{ π} }}D}}} - \left[ {1 - erf{{\left[ {\frac{x}{{2\sqrt D }}} \right]}_t}} \right]\frac{x}{{2D}}} \right] = C\left( {x,t} \right), $ | (3) |
式中:W代表混凝土表面的扩散通量,kg/cm2。W是常量,表示在此环境中氯离子的浓度没有任何变化,但是表面氯离子的浓度与时间的平方根成正比。
4.2.2 氯离子的临界浓度钢筋最开始受到侵蚀的时候,表面处氯离子的浓度称作临界浓度,用Cr表示。氯离子的临界浓度受到多种因素的影响,主要影响因素有水泥的类型、灰水比、水分和可溶解氧的量、温度、粉煤灰的量、酸碱值,还有硅胶的量。在以往的众多研究中,氯离子临界浓度服从均匀分布0.7~1.3 kg/m3。
4.2.3 表面氯离子的浓度由于海洋环境受季节影响比较大,所以混凝土表面的氯离子浓度也在不断变化,选取一个最大值。用C0表示混凝土表面的氯离子浓度。表面氯离子浓度C0与海岸距离d(km)之间的关系如下:
| $ \left. \begin{array}{l} {C_0}\left( d \right) = 0.03{\rm{kg/}}{{\rm{m}}^3},d > 2.84{\rm{km;}}\\ {C_0}\left( d \right) = 1.15 - 1.81{\log _{10}}\left( d \right),0.1{\rm{km}} < d < 2.84{\rm{km;}}\\ {C_0}\left( d \right) = 2.95{\rm{kg/}}{{\rm{m}}^3},d < 0.1{\rm{km}}{\rm{。}} \end{array} \right\} $ | (4) |
氯离子的扩散系数D由很多因素共同决定,并不真实存在,对扩散系数影响最大的是灰水比、硅粉的量和温度。用w/c表示水灰比,a/c为水泥比,DH2O为氯离子在溶液中的扩散系数(NaCl:1.6×10-5cm2/s),可得到它们之间的关系为
| $ D = {\left[ {\frac{{{\rho _c}\frac{w}{c} - 0.85}}{{{\rho _c}\frac{w}{c} + 1}}} \right]^3}\frac{{{\rho _c}\frac{w}{c} + 1}}{{\frac{{{\rho _c}}}{{{\rho _a}}}\frac{a}{c} + {\rho _c}\frac{w}{c} + 1}}0.15{D_{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}。$ | (5) |
在氯离子的作用下建立钢筋的有效面积模型。由于锈蚀的不均匀,锈蚀最大的坑深(Pmax)要远远大于锈蚀均匀的深度(Pav),令Pmax/Pav=T,则P(t)=0.011 6×T×t×icorr,其中P(t)为锈蚀开始t时间后的坑深,mm/y;1 μA/cm2≈11.6 μm/y。
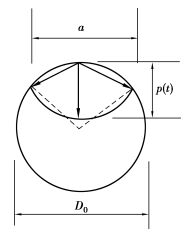
锈蚀的构造如图 3所示。
|
图 3 锈蚀的结构图 |
根据图 3可得出锈蚀的横截面面积Apit与锈蚀的宽度a的关系为
| $ {A_{{\rm{pit}}}}\left( t \right) = \left\{ \begin{array}{l} \frac{{{\rm{ \mathsf{ π} }}D_0^2}}{4},\;\;\;\;{D_0} \le p\left( t \right);\\ \frac{{{\rm{ \mathsf{ π} }}D_0^2}}{4} + {A_2} + {A_1},\;\;\;\;\frac{{{D_0}}}{{\sqrt 2 }} < p\left( t \right) \le {D_0},\\ {A_2} + {A_1},\;\;\;\;p\left( t \right) \le \frac{{{D_0}}}{{\sqrt 2 }}。\end{array} \right.\;\;\;\;a = 2p\left( t \right)\sqrt {1 - {{\left[ {\frac{{p\left( t \right)}}{{{D_0}}}} \right]}^2}} ; $ | (6) |
其中,D0为钢筋的初始直径。A1=0.5[θ1
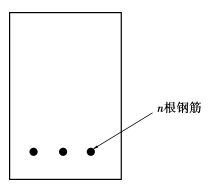
如果钢筋由n个直径为D0的组成,如图 4所示,在氯离子不断的侵蚀作用下,钢筋t时刻的面积为
|
图 4 钢筋的布置 |
| $ {\mathit{A}_{{\rm{st}}}}\left( t \right) = {A_{{\rm{atncm}}}} - \sum\limits_{m = 1}^n {{A_{{\rm{pi}}{{\rm{t}}_{\rm{m}}}}}} , $ | (7) |
在t时刻的时候钢筋的屈服强度标准值为[15]
| $ {f_s} = \left\{ \begin{array}{l} {f_y}\left( {1 - 1.0769{\eta _s}} \right),t \ge {T_i};\\ {f_y}\;\;\;\;\;\;,t < {T_i}。\end{array} \right. $ | (8) |
其中:未被锈蚀的钢筋屈服强度用fy表示;钢筋的截面被破坏的概率,%,用ηs来表示:
| $ {\eta _s}\left( t \right) = \frac{{\sum\limits_{m = 1}^n {{A_{{\rm{pi}}{{\rm{t}}_{\rm{m}}}}}} \left( t \right)}}{{{A_{{\rm{stncm}}}}}}。$ | (9) |
选择截面为圆形的钢筋混凝土受压构件为例,其周围均匀配置了纵向钢筋,它的正截面抗压承载能力为
| $ C\rho {f_{sd}}{r^2} + A{f_{cd}}{r^2} = {N_u}{\gamma _0}。$ | (10) |
抗力函数为
| $ R = {N_u}{K_P} = \left[ {A{f_{cd}}{r^2} + C\rho {f_{{\rm{sd}}}}} \right]{K_P}, $ | (11) |
其中KP为结构构件抗力的相关参数。
4.3.3 混凝土的劣化模型根据研究可知,混凝土的强度不会一成不变,所以不能采用一般的方法来进行描述。对时间比较久的建筑物的混凝土强度进行相关的分析与统计可以发现,混凝土的强度服从正态分布,但随着时间的推移,标准差跟平均值发生了变化。用σf(t),μf(t)表示混凝土在经过了t年之后的标注差和平均值,用σ0和μ0分别表示混凝土在t=0是强度标准差和平均值。他们之间的关系为
| $ \left. \begin{array}{l} {\sigma _f}\left( t \right) = {\sigma _0}\eta \left( t \right),\\ {\mu _f}\left( t \right) = {\mu _0}\xi \left( t \right)。\end{array} \right\} $ | (12) |
通过整理实验数据,进行统计回归,可以得到混凝土强度的经时模型:
| $ \xi \left( t \right) = 1.2448{{\rm{e}}^{ - 0.0347{{\left( {Int - 0.3468} \right)}^2}}}。$ | (13) |
而混凝土强度标准差的模型为
| $ \eta \left( t \right) = 1.0625 + 0.0144t。$ | (14) |
由以上各式可以确定混凝土强度标准差和平均值的变化,预测混凝土结构在使用多年之后的标准差和平均值。
4.4 钢筋锈蚀的屈服强度模型由张平生等的研究可知道,用fyk表示锈蚀钢筋屈服强度的标准值,在t时刻的时候,名义上的锈蚀钢筋的屈服强度的标准值计算公式如下:
| $ \left\{ {\begin{array}{*{20}{c}} {{f_{{\rm{yk}}}}\left( t \right) = {f_{{\rm{yk}}}}\left[ {0.986 - 1.1992\frac{{d_0^2 - {d^2}\left( t \right)}}{{d_0^2}}} \right],t \ge {t_{{\mathop{\rm int}} }};}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f_{{\rm{yk}}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,t < {t_{{\mathop{\rm int}} }}。} \end{array}} \right. $ | (15) |
由于锈蚀开裂钢筋失去了与混凝土的连接,在无粘结预应力钢筋混凝土的应力计算方法上,建立锈蚀开裂后的承载力模型,钢筋锈蚀后的弯曲构件的抗力为
| $ R\left( t \right) = \left[ {1 - \beta \left( t \right)\frac{{{\sigma _s}\left( t \right)}}{{2{f_{{\rm{yk}}}}\left( t \right)}}} \right]{h_0}{\sigma _s}\left( t \right)A\left( t \right)。$ | (16) |
最后钢筋的可靠度指标β可以采用一次二阶矩阵的分析方法计算得到。
5 结束语1) 对海洋环境下氯离子的侵蚀机理进行了分析,氯离子的穿透能力很强,会破坏掉钝化膜,与钢筋表面形成电池反应,钢筋的钝化膜被不断消耗,由于氯离子在整个过程中只是参与反应,不会被消耗,所以电池反应会持续,钢筋的锈蚀会加剧。
2) 对钢筋锈裂的发展过程进行了详细的研究,钢筋最开始只是发生锈蚀,如果在这个阶段没有引起足够的重视,混凝土剥落之后钢筋很容易产生开裂现象,钝化层脱落之后混凝土钢筋结构将不再能够使用,由此得出结论:在钢筋最开始发生锈蚀的时候进行修复取得的效果最好。
3) 建立了钢筋截面积模型,考虑到氯离子浓度的变化,以及钢筋和抗力的劣化,对钢筋混凝土结构的可靠度进行分析。此模型给实际港口及桥梁的钢筋混凝土结构提供了理论依据。
| [1] | 胡亮. 框支短肢剪力墙结构转换梁受力性能分析[D]. 太原: 太原理工大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10112-1011082269.htm |
| [2] |
张伟平, 李士彬, 顾祥林, 等.
自然锈蚀钢筋的轴向拉伸疲劳试验[J]. 中国公路学报, 2009, 22(2): 53–58.
ZHANG Weiping, LI Shibin, GU Xianglin, et al. Experiment on Axial Tensile Fatigue of Naturally Corroded Steel Bar[J]. China Journal of Highway and Transport, 2009, 22(2): 53–58. (in Chinese) |
| [3] |
李颖.
海洋环境下钢筋混凝土结构腐蚀疲劳分析[J]. 山西建筑, 2012, 38(21): 51–53.
LI Ying. Tanalysis on the corrosion and fatigue of steel reinforced concrete structure under the ocean environment[J]. Shanxi Architecture, 2012, 38(21): 51–53. DOI:10.3969/j.issn.1009-6825.2012.21.028 (in Chinese) |
| [4] | 洪定海. 混凝土中钢筋的腐蚀与保护[M]. 北京: 中国铁道出版社, 1998. |
| [5] | Zhang R, Castel A, Francois R. Concrete cover cracking with reinforcement corrosion of rc beam during chloride-induced corrosion process[J]. Cement and Concrete Research, 2010, 40(3): 415–425. DOI:10.1016/j.cemconres.2009.09.026 |
| [6] | 夏晋. 锈蚀钢筋混凝土结构力学性能研究[D]. 杭州: 浙江大学学位论文, 2010. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hygc200302019&dbname=CJFD&dbcode=CJFQ |
| [7] | Mullaed J A, Stewart M G. Corrosion-induced cover cracking of RC structures:new experimental data and predictive models[J]. University of Newcastle, 2009, 275(5): 20. |
| [8] | Chernin L, Val D V, Volokh K Y. Analytical modeling of concrete cover cracking caused by corrosion of reinforcement[J]. Materials and Structures, 2010, 43(4): 543–556. DOI:10.1617/s11527-009-9510-2 |
| [9] | Vu K, Stewart M G, Mullard J. Corrosion-induced cracking:experimental data and predictive models[J]. Structure joural, 2005, 102(5): 719–726. |
| [10] | Wong H S, Zhao Y X, Karimi A R, et al. On the penetration of corrosion products from reinforcing steel into concrete due to chloride-induced corrosion[J]. Corrosion Science, 2010, 52(7): 2469–2480. DOI:10.1016/j.corsci.2010.03.025 |
| [11] | Zhao X Y, Ren H Y, Dai H, et al. Composition and expansion coefficient of rust based on X-ray diffraction and thermal analysis[J]. Corrosion Science, 2011, 53(5): 1646–1658. DOI:10.1016/j.corsci.2011.01.007 |
| [12] | Oh B H, Kim K H, Jang B S. Critical corrosion amount to cause cracking of reinforced concrete structures[J]. ACI Material Journal, 2009, 106(4): 333–339. |
| [13] | Kim K H, Jang S Y, Jang B S, et al. Modeling mechanical behavior of reinforced concrete due to corrosion of steel bar[J]. ACI Structural Journal, 2010, 107(2): 106–113. |
| [14] | Malumbela G, Alexander M, Moyo P. Model for cover cracking of RC beams due to partial surface steel corrosion[J]. Construction and Building Materials, 2011, 25(2): 987–991. DOI:10.1016/j.conbuildmat.2010.06.081 |
| [15] |
朱绩超, 邵旭东.
海洋环境下钢筋混凝土桥梁结构的耐久性评估[J]. 大连理工大学学报, 2010, 31(2): 28–33.
ZHU Jichao, SHAO Xudong. Durability assessment of the reinforced concrete bridge structure under the marine environment[J]. Journal of Dalian University, 2010, 31(2): 28–33. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37


