无线传感器网络(wireless sensor networks)通常采用价格低廉的传感器节点部署, 这些节点之间通过无线通信。传统的目标跟踪算法有最近邻(NN)方法、概率数据关联(PDA)方法、联合概率数据关联(JPDA)方法和多目标跟踪(MHT)算法等。这些方法计算复杂, 不适合资源有限的无线传感器网络^[1]。在当前的相关研究中, 基于单目标的跟踪方法^[2]探讨较多。由于传感器节点的电量受限, 处理性能, 通信带宽, 存储能力等存在问题, 还可能受到实际跟踪目标移动的速度变化和运动方向的随机性等影响, 这种单目标跟踪在能耗和跟踪精度等方面存在严重缺陷。

多目标跟踪指的是将传感器节点接收到的信号数据分解为对应的各种不确定信息源所产生的观测集合或轨迹^[3]。随着WSN应用范围的扩展, 基于WSN实现移动多目标跟踪成为当前研究的热点。在WSN的多目标跟踪研究中, 已有算法主要采用基于关联假设跟踪算法来解决多目标跟踪问题^[4]。另外, 一部分学者则根据WSN节点信号检测能力较弱的特点, 在不考虑数据关联的情况下研究多目标跟踪^[5]。文莎等人^[6]提出采用动态联盟机制进行多目标跟踪协同任务分配, 并对自组织动态联盟进行研究, 采用遗传算法实现盟员选择, 提出了基于面积和的方法来限制节点选择。但是该方法没有较为合理的精度模型, 其跟踪定位和能耗优化存在缺陷。赵欣等人^[7]提出了基于粒子滤波的被动多传感器多目标跟踪算法。该算法利用多个被动传感器的角度观测信息进行交叉定位, 通过模糊概率双加权方式完成目标与定位点的关联匹配, 采用粒子滤波实现非线性运动目标的跟踪。该算法依赖于粒子数的选择, 不同的跟踪目标和状态下其选择粒子数存在较大差异, 因此, 该算法的复杂度极大。

Rad H等人^[8]提出了采用简单预测模型来预测运动跟踪目标位置信息的算法。在该算法中, 采样间隔基于跟踪目标的过去平均移动速度变化。然而, 在采样间隔中并没有考虑跟踪目标方向的变化, 所以, 在抖动较大的环境下, 电量消耗较大, 并且可能存在跟踪目标丢失等问题。Xiao W等人^[9]提出的跟踪机制中, 通过计算采样间隔来保证更新跟踪的准确性。它采用了一种离散搜索最佳采样间隔的方法, 在每个时刻选择一个任务传感器。然而, 选择跟踪精度的阀值会明显的影响总的电量消耗。由于该阀值取决于传感器运动的随机量, 所以很难确定。Lin J等人^[10]提出了一种自适应采样间隔的跟踪机制, 但该研究却没有探讨跟踪目标运动的随机性问题, 例如, 跟踪目标通过急剧弯曲的路径等情况。笔者提出了一种自适应采样间隔的多目标跟踪机制, 设计了一个多目标跟踪的基本框架, 采用跟踪目标的定位元数据实现目标运动模式建模, 基于当前测量的采样间隔和先前采样间隔来预测下一时刻的采样间隔, 以此实现自适应采样过程。基于扩展的卡尔曼滤波器来预测跟踪目标状态, 采用预测目标定位的概率密度函数构建跟踪簇。通过定义跟踪目标中心, 基于马氏距离来量化主节点MN的选举方法, 通过跟踪目标重要性和其与传感器之间的距离来量化目标的影响强度, 并以此作为标准构建多目标选择算法。最后, 基于MATLAB进行了仿真实验, 对比了文献[8], [9], [10]提出的跟踪方法。仿真结果显示, 笔者提出的跟踪机制具备较强的自适应性, 其在WSN网络实现能耗节省的基础上完成了无缝跟踪。

1 WSN多目标跟踪机制的设计

该跟踪机制主要包括采样间隔的设置、跟踪簇的形成、主节点的选举、多目标选择方法的实现等4个部分。

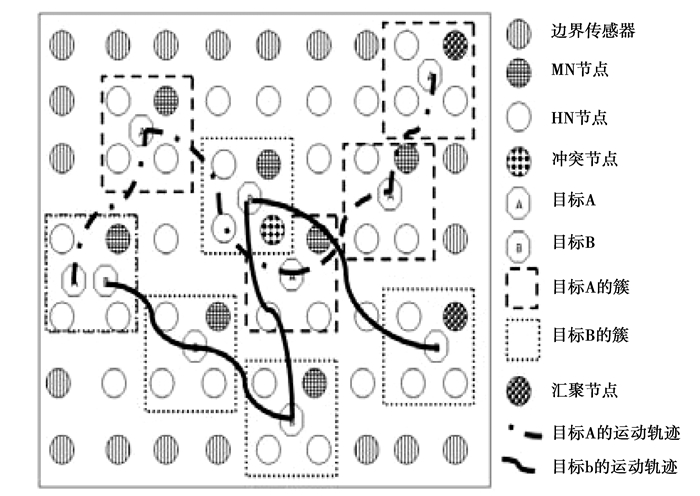
1.1 多目标跟踪框架

研究给出了如图 1所示的一个分布式的多目标跟踪框架。其中边界传感器用来检测目标节点是否移出了WSN感测网络。每个跟踪目标在WSN网络中随机移动, 在每个当前位置, 传感器节点会自动形成一个簇, 其中的一个节点被推举为主节点MN, 其他节点被推举为帮助节点HN, 被多个目标同时构建的簇所占据的节点称为冲突节点。目标最后到达运动终点, 将数据信息送出的MN节点称为汇聚节点。图 1所示的框架中, 设计了2个跟踪目标, 该网络中的传感器节点随机分布, 跟踪目标随机移动。假设在整个WSN中, 所有的传感器节点位置信息相互可知, 边界传感器通常处于全感知或通信模式。为减少电力消耗, 除边界传感器和在某个时刻构建簇的传感器节点外, 其他的传感器节点都处于休眠状态。当这些休眠节点被跟踪目标的新簇纳入后, 则必须被激活, 而离开原簇的传感器节点则必须切换到休眠状态, 以此来实现节能。

提出的目标跟踪机制中, 在每个时刻t_Oj(t), 在簇中选举一个主节点MN_Oj, 其他节点被置为帮助节点HNs_Oj, 簇内所有节点协作跟踪目标T_j, 并通过主节点将跟踪信息传送出去。当跟踪目标进入WSN感测区域后, 跟踪初始化过程就会开始。边界传感器感知跟踪目标后, 采用相关的定位算法实现目标定位(例如三角测量法), 同时, 设置相关的错误协方差(error covariance)。然后, 边界传感器采用卡尔曼滤波来预测下一个跟踪目标状态, 选择更新簇, 执行选择下一个MN_Oj的过程, 初始化采样间隔到其最小值, 激活下一个簇成员到唤醒状态。如果任何节点S_i接受多个请求跟踪目标命令, 则执行分布式的多跟踪目标选择算法来决定其最优跟踪目标。例如在图 1中, 假设跟踪目标A比跟踪目标B更重要, 冲突节点从跟踪目标A接收到的跟踪目标影响强度比跟踪目标B接收到的要大。因此, 冲突节点将服务跟踪目标A, 跟踪目标B的MN将会重新选择新的帮助节点。

在每个时刻t_Oj(t), 跟踪目标元数据TMD_Oj(t)由跟踪目标标识符, 类型符Z_Oj(t), 定位元数据M_Oj(t, T_m), 采样时间间隔Δt_Oj(t)和跟踪目标元数据建立时的时戳构成。其中M_Oj(t, T_m)包括了最后一个T_m≤t时的跟踪目标更新位置预测状态$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }}_{{O_j}}$$\left( {t + 1|t} \right)$和协方差矩阵P_Oj(t+1|t)。

当前簇主动发送跟踪目标元数据到下一个簇, 新簇在跟踪目标到达其附近前就能获取跟踪目标信息。如果在跟踪过程中出现某些传感器节点同时跟踪多个目标, 则这些节点被称为冲突节点。为保证跟踪的可靠性, 必须保证冲突节点只跟踪单一目标, 故采用目标分类标识符信息实现冲突处理。

1.2 自适应采样间隔的设置

提出的跟踪机制中, 目标运动模式使用定位元数据进行建模。跟踪目标O_j的最后一个跟踪热点T_m的定位元数据M_Oj(t, T_m)计算如下

$ {M_{{O_j}}}\left( {t, {T_m}} \right){\rm{ = }}\frac{{{d_{{O_j}}}\left( t \right)}}{{{d_{{O_j}}}\left( {t, {T_m}} \right)}}, $

(1)

其中:d_Oj(t)是在最后一个跟踪热点T_m时的跟踪目标网络遍历值; d_Oj(t, T_m)是在最后一个跟踪热点T_m时的跟踪目标总的网络遍历值。当跟踪目标采用完全统一的方式移动时, M_Oj(t, T_m)是整体一致的。当跟踪目标弯曲移动时, 它就会减小。d_Oj(t)和d_Oj(t, T_m)的计算如下

$ {d_{{O_j}}}\left( t \right) = \sqrt {{{\left[{{{\hat L}_{{\rm{diff}}{1_j}}}} \right]}^\prime }\left[{{{\hat L}_{{\rm{diff}}{1_j}}}} \right]}, $

(2)

$ {d_{{O_j}}}\left( {t, {T_m}} \right) = \sum\limits_{j = t - {T_m}}^{t - 1} {\sqrt {{{\left[{{{\hat L}_{{\rm{diff}}{{\rm{2}}_j}}}} \right]}^\prime }\left[{{{\hat L}_{{\rm{diff}}{{\rm{2}}_j}}}} \right]} }, $

(3)

在此${{\hat L}_{{\rm{diff}}{1_j}}} = {{\hat L}_{{O_j}}}\left( {t|t} \right) - {{\hat L}_{{O_j}}}\left( {t - {T_m}|t - {T_m}} \right), {{\hat L}_{{\rm{diff}}{{\rm{2}}_j}}} = {{\hat L}_{{O_j}}}\left( {j|j} \right) - {{\hat L}_{{O_j}}}\left( {j + 1|j + 1} \right), {{\hat L}_{{O_j}}}\left( {t|t} \right) = \left[{{{\mathit{\boldsymbol{\hat x}}}_{{O_j}}}\left( t \right){{\hat y}_{{O_j}}}\left( {t|t} \right)} \right]$, 表示跟踪目标定位的更新。当跟踪目标回归到和最后一个跟踪热点T_m相同的起始位置, 并且其最大值和总的遍历相同时(假设在最后一个跟踪点T_m, 跟踪目标沿直线移动), 网络遍历的最小值为0。此时, 定位元数据处于区间0≤M_Oj(t, T_m)≤1。

假设Δt_Oj(t)表示当前的采样时间间隔, 它是区间T_min≤Δt_Oj(t)≤T_max上的自适应变量。T_min表示最小采样间隔, 其值小于信道接入时间、传播延迟和其他相关的数据处理时间。T_max表示最大采样间隔, 其根据跟踪目标运动的随机性和数量决定。Δt_Oj(t)基于当前的定位元数据M_Oj(t, T_m)和先前的采样间隔Δt_Oj(t-1)计算。设测量时间间隔为Δt_mOj(t), 其中T_min≤Δt_mOj(t)≤T_max。Δt_mOj(t)是定位元数据的线性函数, 如果Δt_mOj(t)=f(M_Oj(t, T_m)), 则有

$ \Delta {t_{m{O_j}}}\left( t \right) = \left( {{T_{\max }} - {T_{\min }}} \right){M_{{O_j}}}\left( {t, {T_m}} \right) + {T_{\min }}, $

(4)

因此, 当前采样时间间隔Δt_Oj(t)是测量采样间隔Δt_mOj(t)和先前采样间隔Δt_Oj(t-1)的加权和, 如公式(5)所示

$ \Delta {t_{{O_j}}}\left( t \right) = \alpha \Delta {t_{{O_j}}}\left( {t - 1} \right) + \left( {1 - \alpha } \right)\Delta {t_{m{O_j}}}\left( t \right), $

(5)

其中α∈[0, 1]。

1.3 跟踪簇的形成

设计的跟踪算法中, 每个跟踪目标对应一个跟踪簇, 每个跟踪簇由多个传感器构成。随着跟踪目标的运动, 簇内节点不断产生变化, 部分节点可能加入该簇, 其他部分节点可能要离开原簇。跟踪簇的形成基于预测跟踪目标定位概率密度函数来实现。

为提高预测目标定位的准确性, 采用了扩展的卡尔曼滤波器(EKF)来预测跟踪目标状态。EKF是一个数学模型, 它使用噪声测量来计算估计值。卡尔曼滤波器是基于线性化的非线性动态测量模型, 它考虑条件的均值和协方差。假设在时刻t_Oj(t), EKF预测其下一个时刻t_Oj(t+1)的目标状态向量$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }}_{{O_j}}$ $\left( {t + 1|t} \right)$和协方差矩阵P_Oj(t+1|t)。在时刻t+1, EKF计算更新的目标状态向量$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }}_{{O_j}}\left( {t + 1|t} \right)$ , 更新与其相关的协方差矩阵P_Oj(t+1|t), 其预测状态表示如下

$ {{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }}}_{{O_j}}}\left( {t + 1|t} \right) = {A_{{O_j}}}\left( t \right){{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }}}_{{O_j}}}\left( {t|t} \right), $

(6)

相关的预测协方差矩阵表示如下

$ {\mathit{\boldsymbol{P}}_{{O_j}}}\left( {t + 1|t} \right) = {A_{{O_j}}}\left( t \right){\mathit{\boldsymbol{P}}_{{O_j}}}\left( {t|t} \right){{A'}_{{O_j}}}\left( t \right) + {Q_{{O_j}}}\left( t \right), $

(7)

假设x_Oj(t+1)=$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }}_{{O_j}}\left( {t + 1|t} \right)$ =[H_ij], 1≤i≤n_g, 1≤j≤4, 则有

$ {H_{ij}} = \left\{ {\begin{array}{*{20}{c}} {\frac{{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_{{O_j}}}\left( {t + 1|t} \right) - {x_{{s_i}}}}}{{\sqrt {{{\left[{{{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over L} }}}_{{O_j}}}\left( {t + 1|t} \right)-{L_{{S_i}}}} \right]}^\prime }\left[{{{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over L} }}}_{{O_j}}}\left( {t + 1|t} \right)-{L_{{S_i}}}} \right]} }}\;}&{j = 1}\\ {}&{j = 2}\\ {\frac{{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over y} }_{{T_j}}}\left( {t + 1|t} \right) - {y_{{s_i}}}}}{{\sqrt {{{\left[{{{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over L} }}}_{{O_j}}}\left( {t + 1|t} \right)-{L_{{S_i}}}} \right]}^\prime }\left[{{{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over L} }}}_{{O_j}}}\left( {t + 1|t} \right)-{L_{{S_i}}}} \right]} }}}&{j = 3} \end{array}} \right., $

(8)

其中, ${{\mathit{\boldsymbol{\hat L}}}_{{O_j}}}\left( {t + 1|t} \right) = {\left[{{{\hat x}_{{O_j}}}\left( {t + 1|t} \right){{\hat y}_{{O_j}}}\left( {t + 1|t} \right)} \right]^\prime }$是预测目标的定位向量。在每个时刻t, 受跟踪目标影响最大的传感器节点自动构建跟踪簇。假设簇S_g(Oj)(t+1)将在时刻t+1跟踪目标, 通过马氏距离D_Oj(t+1|t, S_i)来选择形成跟踪簇的节点。在马氏距离的计算中考虑预测跟踪目标定位协方差P_Oj(t+1|t)。通过跟踪目标的预测定位概率密度函数和当前主节点MN的每个邻居节点S_i计算马氏距离D_Oj(t+1|t, S_i), 如公式(9)所示

$ {D_{{O_j}}}\left( {t + 1|t, {S_i}} \right) = \sqrt {{{\left[{{L_{{S_i}}}-{{\mathit{\boldsymbol{\hat L}}}_{{O_j}}}\left( {t + 1|t} \right)} \right]}^\prime }{P_{{O_j}}}\left( {t + 1|t} \right)\left[{{L_{{S_i}}}{\rm{-}}{{\mathit{\boldsymbol{\hat L}}}_{{O_j}}}\left( {t + 1|t} \right)} \right]} 。$

(9)

P_Oj(t+1|t)是预测跟踪目标定位协方差矩阵, 对于i, j∈[1,4], 如果采用P_Oj(t+1|t)=[P_ij]的形式进行描述, 则P_Oj(t+1|t)计算如下

$ {\mathit{\boldsymbol{P}}_{{O_j}}}\left( {t + 1|t} \right) = \left[{\begin{array}{*{20}{c}} {{P_{11}}}&{{P_{13}}}\\ {{P_{31}}}&{{P_{33}}} \end{array}} \right]。$

(10)

跟踪目标影响强度G_Oj(t+1|t, S_i)定义如下

$ {G_{{O_j}}}\left( {t + 1|t, {S_i}} \right) = \frac{{{Z_{{O_j}}}\left( {t + 1} \right)}}{{{D_{{O_j}}}\left( {t + 1|t, {S_i}} \right)}}。$

(11)

在此, Z_Oj(t+1)表示跟踪目标的重要性, 选择适配函数的计算如下

$ {f_{S\left( {{O_j}} \right)}}\left[{t + 1|t, {S_i}} \right]{\rm{ = }}\frac{{{G_{{O_j}}}\left( {t + 1|t,{S_i}} \right)}}{{\sum\nolimits_{\forall \;\ell \in {S_{n\left( {{O_j}} \right)}}^{\left( k \right)}} {{G_{{O_j}}}\left( {t + 1|t, {S_\ell }} \right)} }}。$

(12)

如果第m个簇S_m(Oj)∈S_g(Oj)(t+1)1≤l≤n_g被选择, 则有

$ \begin{array}{l} {S_{m\left( {{O_j}} \right)}} = {\arg _{{S_i}}}\max \left\{ {{f_{S\left( {{O_j}} \right)}}\left[{t + 1|t, {S_i}} \right]} \right\}, \\ {S_i} \in {S_{m\left( {{O_j}} \right)}}\backslash \bigcup\nolimits_{m = 1}^{\ell = m - 1} {{S_{\ell \left( {{O_j}} \right)}}}, \end{array} $

(13)

其中${S_{m\left( {{O_j}} \right)}}\backslash \bigcup\nolimits_{m = 1}^{\ell = m - 1} {{S_{\ell \left( {{O_j}} \right)}}} $表示排除S₁到S_m-1的集合S_m(Oj)的成员。

1.4 主节点的选举

研究提出的机制中, 每个构建的跟踪簇中包括一个主节点MN和多个帮助节点HNs。因此, 合理选择MN是实现WSN节能和网络生存时间的重要保证。假设, 对于跟踪目标O_j, C_Oj(t+1, S_i)表示节点S_i(S_i∈S_g(Oj)(t+1))在时刻t+1的节点中心, 其计算如下

$ {C_{{O_j}}}\left( {t + 1, {S_i}} \right) = \frac{1}{{\sum\nolimits_{\forall \;j \in {S_{g\left( {{O_j}} \right)}}^{\left( {t + 1} \right)}} {\sqrt {{{\left[{{L_{{S_i}}}-{L_{{S_j}}}} \right]}^\prime }\left[{{L_{{S_i}}}-{L_{{S_j}}}} \right]} } }}。$

(14)

负载均衡是选举MN节点需要考虑的重要因素, 通过选择具有最大剩余电量的节点做MN可以提高整个系统的负载均衡性能。设f_E(Oj)[t+1, S_i]是传感器节点S_i的选择适配函数, 其计算如下

$ \begin{array}{l} {f_{E\left( {{O_j}} \right)}}\left[{t + 1, {S_i}} \right] = \beta \times \frac{{{C_{{O_j}}}\left( {t + 1, {S_i}} \right)}}{{\sum\nolimits_{\forall \;j \in {S_{g\left( {{O_j}} \right)}}^{\left( {t + 1} \right)}} {{C_{{O_j}}}\left( {t + 1, {S_i}} \right)} }} + \left( {1 + \beta } \right) \times \frac{{{E_{{S_i}}}}}{{\sum\nolimits_{\forall \;j \in {S_{g\left( {{O_j}} \right)}}^{\left( {t + 1} \right)}} {{E_{{S_i}}}} }}, \end{array} $

(15)

在此, E_Si表示节点S_i的剩余电量, $δ$∈[0, 1]是用于实现电能消耗负载均衡的加权参数。因此, 下一个被选择的MN_Oj(t+1)具有最大的选择适配函数f_E(Oj), 该节点计算如下

$ M{N_{{O_j}}}\left( {t + 1} \right) = {\arg _{{S_i}}}\max {f_{E\left( {{O_j}} \right)}}\left[{t + 1, {S_i}} \right]。$

(16)

1.5 多目标选择方法

冲突节点S_c可以在检测到跟踪目标集S_O的同时通过运行多目标选择算法来决定其首选跟踪目标。通常采用跟踪目标的重要性和跟踪目标与传感器之间的距离来量化跟踪目标的影响强度。

如果2个跟踪目标的重要性相同, 冲突节点将选择距离更近的跟踪目标；如果2个跟踪目标到冲突节点的距离相同时, 冲突节点将选择重要性更强的跟踪目标, 否则, 会通过计算跟踪目标重要性和距离的比例来进行跟踪目标选择。该分布式多目标选择算法描述如下

int j=1, n=100;//设置初始化的传感器数量

int t=0, p, t;

float G_max; //定义最大的跟踪目标影响强度

float Z_O1(t+1)=h_O1[t+1, x_O1(t+1)]+v_O1(t+1)

//最大目标重要性的初始计算

float $G\left( {{O_1}, {S_c}} \right) = \frac{{{Z_{{O_1}}}\left( {t + 1} \right)}}{{D\left( {{O_1}, {S_c}} \right)}}$

//最大目标重要强度的初始计算

Z_max=Z_O1(t+1) //最大目标重要性的初值

G_max=G(O₁, S_c) //最大目标重要强度的初值

for (j=2; j < =n; j++)//T_j∈S_T

{

$G\left( {{O_1}, {S_c}} \right) = \frac{{{Z_{{O_1}}}\left( {t + 1} \right)}}{{D\left( {{O_1}, {S_c}} \right)}}$

if (G_max < G(O_j, S_c)

{

G_max=G(O_j, S_c)

t=j;

}

  select(O_k)

//选择最大跟踪目标影响强度G(O_j, S_c)的跟踪目标O_k

  else

if(G_max=G(O_j, S_c) & Z_max < Z_Oj(t+1))

  {

  Z_max=Z_Oj(t+1)

  p=j;

}

  select(O_p)//选择具有最大G(O_j, S_c)的跟踪目标O_p

}

  if (monitor(O_j)=S_r & O_j≠O_r)

//簇Group_jS_g^c的成员S_r用来跟踪目标O_j, 并且O_j≠O_r。

if (S_r=node(MN_j)// S_r是MN节点

{

reform(Group_j) //重组簇

re-elect(node(MN_j+1))//选举新的主节点

  }

  else

  if(S_r=node(HNs_j))

  Add(Group_j+1, S_r) //加入选择跟踪目标T_s的簇

  }

2 仿真分析

基于MATLAB对所提出的多目标跟踪机制进行了仿真分析。整个实验中, 设置了3个不同的跟踪目标, 从当前固定的统一点进入感测区域, 沿随机方向向前运动。当跟踪目标到达感测区域边源时, 它会随机的改变方向, 使其保持在感测区域内移动。通过实验分析了所提出机制的跟踪预测轨迹和实际轨迹对比, 同时, 对比了针对3个不同目标运动轨迹实现的自适应采样间隔情况。最后和文献[8], [9], [10]提出的方法进行了能耗对比。相关的仿真环境如表 1所示。

2.1 跟踪预测轨迹和实际轨迹对比

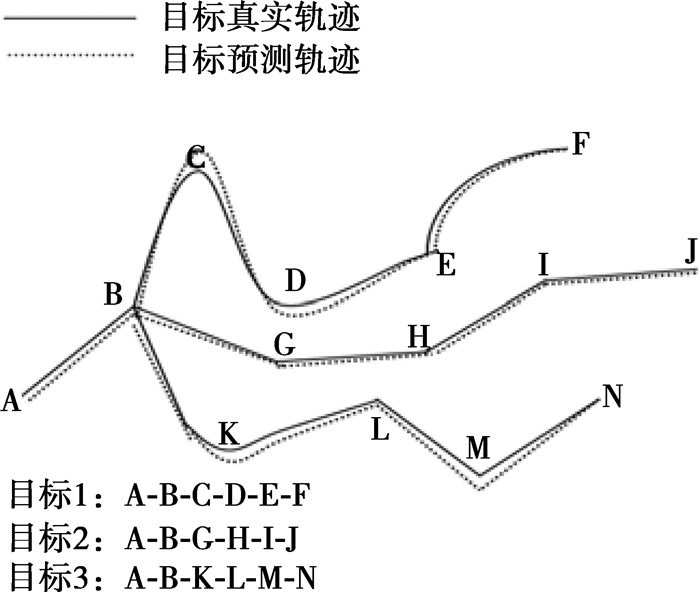
实验中, 设计的3个跟踪目标从相同的A点出发, 沿着不同的位置和方向分别到达F、J、N点, 跟踪目标均在传感器网络构成的感测区域中运行, 3个目标的重要性分别为60, 50, 40, 3个目标均采用速度为5 m/s的速度匀速运动, 移动距离均为900 m, 执行时间为180 s。在图 2中标出了真实的跟踪目标轨迹和采用提出的机制估算的跟踪目标轨迹的对比值。所有跟踪目标的初始化协方差矩阵为10I, I表示单位矩阵阵, O_j的跟踪更新错误采用跟踪更新状态协方差矩阵P_Oj(t|t)来定义。可以看到估计的轨迹和真实轨迹十分接近。

2.2 采样间隔分析

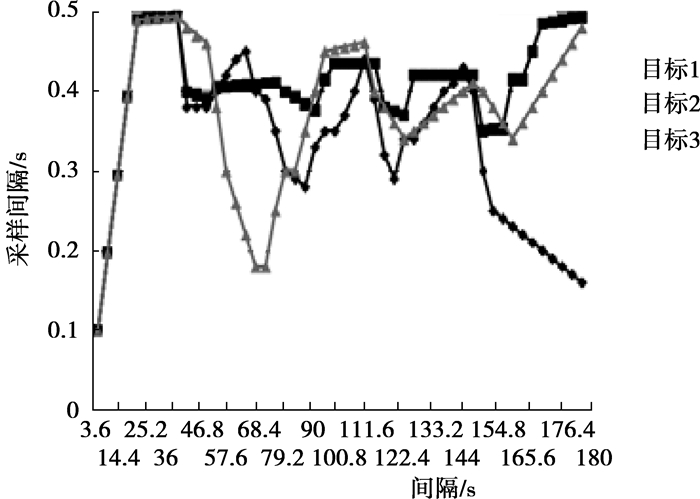
图 3展示了3个跟踪目标的采样间隔, 同样采用相同的实验环境, 测量的采样间隔适合于定位元数据。因此, 采样间隔是测量的采样间隔和先前的采样间隔的权值之和。当跟踪目标沿着同一路径运动时, 采样间隔就很大, 因此可以改善能耗。另一方面, 当跟踪目标急剧运动时, 采样间隔就会减少, 这样跟踪的精度就会增加, 能实现无缝跟踪。

2.3 算法的能耗对比

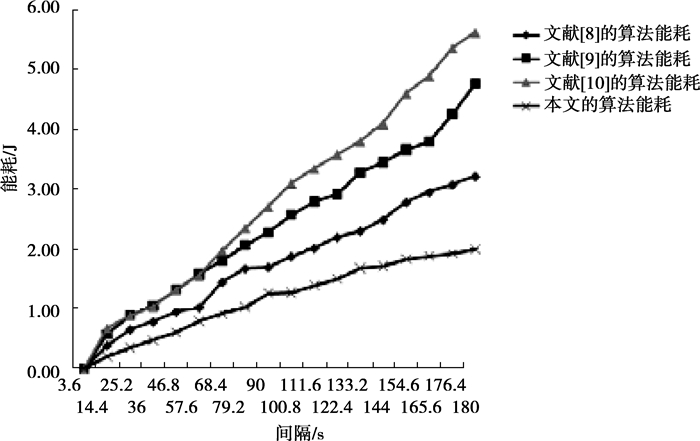
对提出的算法和文献[8-10]3种算法的能耗对比分析。考虑到跟踪目标的匀速运动, 假设在某个时刻t, 量化跟踪目标构建的簇为一个较均匀的圆形区域, 假定跟踪目标在不同时刻处于不同位置的大小相同的圆形跟踪区域内, 以此构建能耗模型。建立的能耗模型主要考虑每个时刻构建的跟踪簇内节点的发送和接收跟踪数据的总能耗情况。为实现测试的可靠性, 每个算法平均执行30次, 每次执行180 s的时间。

通过执行的结果统计分析(如图 4), 文献[8]的算法总耗能为3.209 J, 文献[9]的算法总耗能为4.765 J, 文献[10]的算法总耗能为5.624 J, 提出的算法的总能耗为1.984 J。可以看到前面这3种算法的能耗分别比提出的算法高出61.74%、140.17%和183.47%, 笔者所提出的算法具备较大的能耗改进。

3 结论

提出了一种自适应采样间隔的无线传感器网络多目标跟踪机制, 设计了一个多目标跟踪的基本框架, 采用跟踪目标的定位元数据来对目标的运动模式进行建模, 基于实际测量采样间隔和先前采样间隔来预测下一时刻的采样间隔, 以此实现自适应的采样过程。基于扩展的卡尔曼滤波器来预测跟踪目标状态, 采用预测目标定位的概率密度函数来实现跟踪簇, 通过定义跟踪目标中心, 基于马氏距离来量化主节点MN的选举方法, 通过跟踪目标重要性和其与传感器之间的距离来量化目标的影响强度, 并以此为标准构建了多目标的选择方法。

基于MATLAB进行了仿真实验, 实验结果显示, 所提出机制的跟踪预测轨迹和实际轨迹较为接近, 表明该算法具备较准确的目标跟踪性能。通过3个不同运动目标的采样间隔分析, 得出该算法在目标急剧变化运动方向时, 采样间隔就会变小, 当目标沿着相对平直路线运动时, 采样间隔就会增加, 实现了自适应的跟踪过程。对比分析了文献[8], [9], [10]提出的方法, 结果显示, 提出的算法具备较强的自适应性, 其在实现WSN网络能耗节省的基础上达到了无缝跟踪。值得一提的是, 由于仅考虑的仅是跟踪目标匀速运动情况下的性能分析, 对于现实中考虑到跟踪目标运动速度不断变化, 或者受到实际运动环境的影响等进行的跟踪性能分析没有讨论, 该方面将是日后研究的新课题。