1. 重庆大学 机械传动国家重点实验室,重庆 400044;
2. 重庆望江工业集团公司,重庆 400071
收稿日期: 2014-11-12
基金项目: 国家科技支撑计划资助项目(2012BAA01B05);重庆市重点攻关项目(CSTC2014YYKFB9003)
1. The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, P.R.China;
2. Chongqing Wangjiang Industrial Co.Ltd., Chongqing 400071, P.R.China
Supported by National Key Technology Support Program (2012BAA01B05) and the Key Science and Technology Projects Fund of Chongqing (CSTC2014YYKFB9003)
伴随着国家支持和环境对发展清洁能源的需求,风力发电市场发展迅猛,2013年中国新增装机容量16 088 MW,累计装机容量91 412 MW,新增装机和累积装机两项数据均居世界第一。随着风力发电市场的发展,风机频发的故障成了主要待解决的问题,提高风机设计可靠性成了一个风机的主要研究方向[1]。
风力发电机组主要由气动系统、传动链系统、电气系统和控制系统组成,在风力发电机发电的过程中,其传动链往往受到时变风载,紧急停车,塔筒的晃动以及冬夏温差等因素的影响,这些因素都影响着传动链的工作性能,导致传动系统故障频发。目前国内外学者对风电机组传动系统进行了一定的研究,胥良考虑极限和额定载荷工况,对兆瓦级风电齿轮箱的关键零部件进行静力学分析,得到齿轮箱箱体、行星架的应力云图以及极限载荷系数[2]。陈爽利用campell分析、模态能量分布分析和阶次扫频分析等手段对风电齿轮箱传动系统潜在共振进行了分析[3]。徐向阳利用动力学方法,对柔性销轴式风电齿轮箱的均载、耦合特性与动态特性等展开了研究[4]。朱才朝等人建立了风电齿轮箱外啮合和内啮合的有限元模型,提出了一种计算齿轮啮合过程中实际接触齿数、齿间载荷分配与齿面载荷分配的方法,并对风电齿轮箱的共振特性展开相关研究[5-6];秦大同等人针对风力发电机对齿轮箱的高可靠性要求,提出了一种加速疲劳试验技术方法来验证齿轮箱的疲劳程实时在线测试和评价[7]。综上所述,现有文献在对风机的理论、风场测试和台架实验进行研究时,均忽略了塔筒的摆动与扭转对风电机组传动链的影响。研究以主流兆瓦级风点机组传动链结构为研究对象,考虑风机塔筒的摆动与风机传动链的扭转振动耦合效应,利用集中参数法对风机传动链动态特性进行研究。
1 兆瓦级风电机组传动链结构与原理
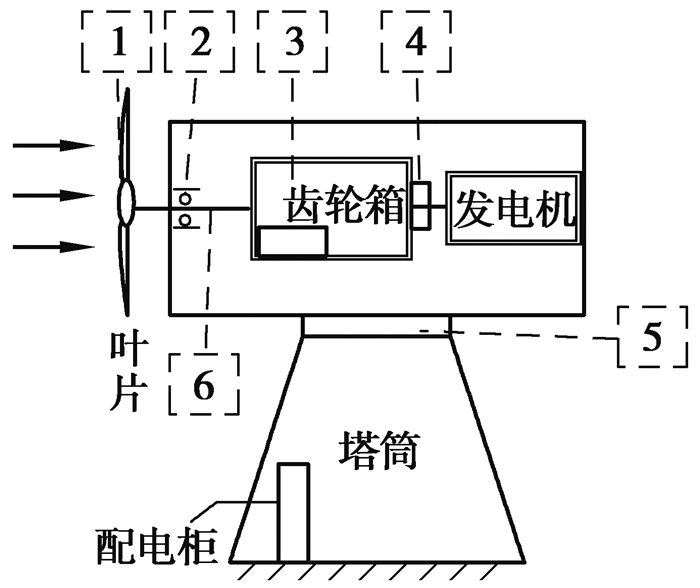
目前风机主要有直驱型风机、半直驱型风机和双馈型风机,其中以双馈型为主。国内各风场以水平式的风机结构为主,如图 1所示为水平式某兆瓦风力发电机组传动链结构简图,机舱位于近100 m的塔筒顶端,齿轮箱位于塔筒中部,通过主轴轴承与扭力臂固定在机舱中,利用叶片将风能转化为机械能。叶片固定在轮毂上并通过轮毂带动主轴转动,主轴通过锁紧盘与齿轮箱行星架相连接,通过齿轮箱升速将主轴上的低转速大扭矩动能转化为高转速低扭矩的动能,带动发电机进行发电。
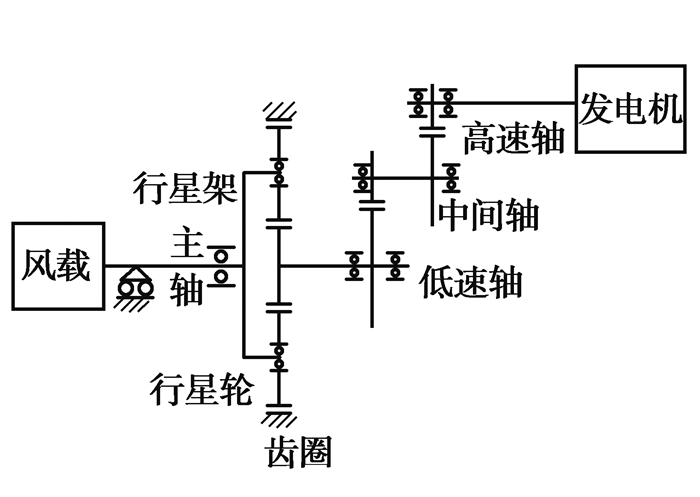
图 2所示为风电齿轮箱结构简图,主轴通过锁紧盘带动行星架转动,行星轮安装在行星架上,同时与内齿圈和太阳轮啮合,进而带动太阳轮转动,太阳轮与低速轴为一体设计,低速轴通过花键带动中间级主动轮转动,第二级和第三极为大齿轮与小齿轮进行啮合升速,最终将主轴的低转速大扭矩动能转化为适应发电机发电频率的高转速低扭矩的动能。
2 兆瓦级风电机组传动链动力学建模
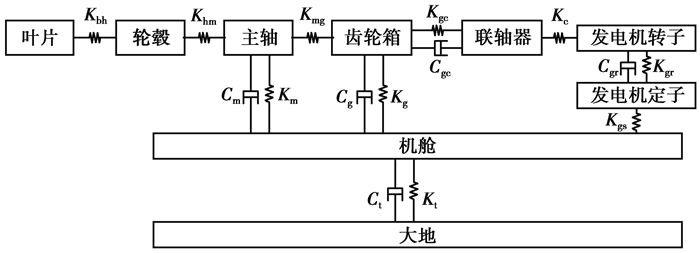
某三点支撑的兆瓦级风电机组传动链连接拓扑关系如图 3所示,其中叶片根部与轮毂固定连接,轮毂与主轴连接,主轴利用锁紧盘与齿轮箱上的行星架相连接,同时通过主轴轴承支撑在机舱上,齿轮箱通过左右2个扭力臂支撑在机舱上,同时通过齿轮高速轴与联轴器连接,联轴器与发电机转子连接,发电机定子通过轴承支撑机舱上,机舱由塔架支撑。
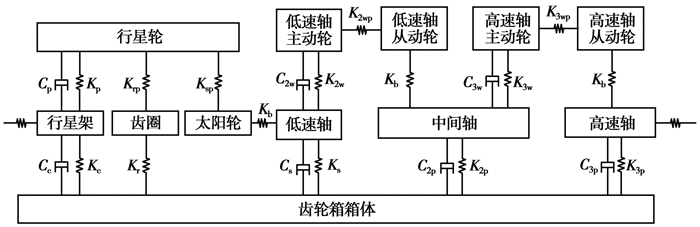
齿轮箱是传动链的重要部件,其结构和受力较为复杂。为了对传动链的动态特性进行深入分析,将图 3中的齿轮箱内部连接拓扑关系进行细化,如图 4所示为齿轮箱内部结构拓扑关系图。风力发电机拓扑图符合含义如表 1所示,齿轮箱拓扑图符合含义如表 2所示。
表 1(Table 1)
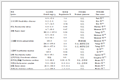
表 1 风力发电机拓扑图符号
Table 1 Symbols in the topological diagram of wind turbine
| 符号 |
含义 |
| Kbh |
叶片支撑刚度 |
| Kmg |
锁紧盘支撑刚度 |
| Kc |
轴刚度 |
| Kg/Cg |
扭力臂支撑刚度与阻尼 |
| Kgs |
发电机定子支撑刚度 |
| Khm |
轮毂支撑刚度 |
| Kgc/Cgc |
联轴器刚度与阻尼 |
| Km/Cm |
主轴轴承刚度与阻尼 |
| Kgr/Cgr |
发电机转子轴承刚度与阻尼 |
| Kt/Ct |
塔筒刚度与阻尼 |
|
表 1 风力发电机拓扑图符号
Table 1 Symbols in the topological diagram of wind turbine
|
表 2(Table 2)

表 2 齿轮箱拓扑图符号
Table 2 Symbols in the topological diagram of wind turbine gearbox
| 符号 |
含义 |
| Kc/Cc |
行星架轴承支撑刚度与阻尼 |
| Ks/Cs |
低速轴轴承支撑刚度与阻尼 |
| K2p/C2p |
中间轴轴承支撑刚度与阻尼 |
| K2w/C2w |
低速轴主动轮支撑刚度与阻尼 |
| Krp |
齿圈与行星轮啮合刚度 |
| K2wp |
中间级齿轮啮合刚度 |
| Kb |
绑定约束 |
| Kp/Cp |
行星轮轴承支撑刚度与阻尼 |
| Kr |
齿圈扭转刚度 |
| K3p/C3p |
高速轴轴承支撑刚度与阻尼 |
| K3w/C3w |
高速轴主动轮支撑刚度与阻尼 |
| Ksp |
行星轮与太阳轮啮合刚度 |
| K3wp |
高速级齿轮啮合刚度 |
|
表 2 齿轮箱拓扑图符号
Table 2 Symbols in the topological diagram of wind turbine gearbox
|
由于叶片连接在轮毂上,不考虑变桨时,可以将其考虑为固定连接,而轮毂固定于主轴前端,因此将叶片与轮毂的质量和转动惯量换算到主轴上,根据上述兆瓦级风电机组传动链拓扑图模型和齿轮箱拓扑关系模型,利用拉格朗日法建立系统动力学模型。其中系统动能为
|
T=1/2(Imx˙θ2mx+Imy˙θ2my+Imz˙θ2mz+Icx˙θ2cx+Icy˙θ2cy+Icz˙θ2cz+Isx˙θ2sx+Isy˙θ2sy+Isz˙θ2sz+Irx˙θ2rx+Iry˙θ2ry+Irz˙θ2rz+N∑i=1Ipiu˙θ2piu+N∑i=1Ipiv˙θ2piv+N∑i=1Ipiw˙θ2piw++I2wx˙θ22wx+I2wy˙θ22wy+I2wz˙θ22wz+I2px˙θ22px+I2py˙θ22py+I2pz˙θ22pz+I3wx˙θ23wx+I3wy˙θ23wy+I3wz˙θ23wz+I3px˙θ23px+I3py˙θ23py+I3pz˙θ23pz+Igx˙θ2gx+Igy˙θ2gy+Igz˙θ2gz+Ipy˙θ2py+Ipz˙θ2pzmm˙x2n+mm˙y2m+mm˙z2m+mc˙x2c+mc˙y2c+mc˙z2c+ms˙x2s+ms˙y2s+ms˙z2s+mr˙x2r+mr˙y2r+mr˙z2r+N∑i=1mpi˙u2pi+N∑i=1mpi˙v2pi+N∑i=1mpi˙w2pi+m2w˙x22w+m2w˙y22w+m2wz˙x22w+m2p˙x22p+m2p˙y22p+m2p˙z22p+m3w˙x23w+m3w˙y23wm3w˙z23w+m3p˙x23p+m3p˙y23p+m3p˙z23p+mg˙x2g+mg˙y2g+mg˙z2g+mp˙x2p+mp˙z2p+mt˙x2t+mt˙z2t),
|
(1) |
式中:T为系统动能;下标m表征传动主轴;c表征行星架;s表征太阳齿轮;r表征齿圈;pi表征第i个行星齿轮;2w表征齿轮箱中间级大齿轮;2p表征齿轮箱中间级小齿轮;3w表征齿轮箱高速级大齿轮;3p表征齿轮箱高速级小齿轮;g表征齿轮箱箱体;p表征齿轮箱支撑;t表征塔筒;u、v、w为行星齿轮坐标系,x,y,z为坐标系方向自由度,θx,θy,θz为扭转方向自由度,I为转动惯量,m为构建质量。
系统势能
|
U=Uspi+Urpi+Ub+U2wp+U3wp,
|
(2) |
式中:Uspi为太阳行星齿轮啮合势能;Urpi为齿圈行星齿轮啮合势能;Ub为轴承支撑势能;U2wp为中间级齿轮啮合势能;U3wp为高速级齿轮啮合势能。
其中
|
Uspi=1/2N∑i=1Kspiδ2spi,
|
(3) |
|
Urpi=1/2N∑i=1Krpiδ2rpi,
|
(4) |
|
Ub=1/2(Kmθxθ2mx+Kmθyθ2my+Kmxx2m+Kmyy2m+Kmzz2m)+1/2(Kcθxθ2cx+Kcθyθ2cy+Kcxx2c+Kcyy2c+Kczz2c)+1/2(Ksθxθ2sx+Ksθyθ2sy+Ksxx2s+Ksyy2s+Kszz2c)+1/2N∑i=1(Kpiuθ2piu+Kpivθ2piv+Kpiuδ2piu+Kpivδ2piv+Kpiwδ2piw)+1/2(Krθxθ2rx+Krθyθ2ry+Krθzθ2rz+Krxx2r+Kryy2r+Krzz2r)+1/2(K2wθxθ22wx+K2wθyθ22wy+K2wxx22w+K2wyy22w+K2wzz22w)+1/2(K2pθxθ22px+K2pθyθ22py+K2pxx22p+K2pyy22p+K2pzz22p)+1/2(K3wθxθ23wx+K3wθyθ23wy+K3wxx23w+K3wyy23w+K3wzz23w)+1/2(K3pθxθ23px+K3pθyθ23py+K3pxx23p+K3pyy23p+K3pzz23p)+1/2(Kgθxθ2gx+Kgθyθ2gy+Kgθzθ2gz+Kgxx2g+Kgyy2g+Kgzz2g)+1/2(Kpθyθ2py+Kpxx2p+Kpzz2p)+1/2(Ktθyx2ty+Ktxx2t+Ktzz2t),
|
(5) |
式中,Kspi为太阳行星齿轮啮合刚度;δspi为太阳行星齿轮啮合向等效振动位移[8-11]。Krpi为齿圈行星齿轮啮合刚度;δrpi为齿圈行星齿轮啮合向等效振动位移;Kmθx为主轴x轴扭转向支撑刚度;δ2wp为中间级齿轮啮合向等效振动位移;δ3wp为高速级齿轮啮合向等效振动位移。
系统耗散能
|
R=Rspi+Rrpi+Rb+R2wp+R3wp,
|
(8) |
式中:Rspi为太阳行星齿轮啮合耗散能;Rrpi为齿圈行星齿轮啮合耗散能;Rb为系统支撑耗散能;R2wp为中间级齿轮啮合耗散能;R3wp为高速级齿轮啮合耗散能。
其中
|
Rspi=1/2N∑i=1Cspiδ2spi,
|
(9) |
|
Rrpi=1/2N∑i=1Crpiδ2rpi,
|
(10) |
|
Rb=1/2(Cmθx˙θ2mx+Cmθy˙θ2my+Cmx˙x2m+Cmy˙y2m+Cmz˙z2m)+1/2(Ccθx˙θ2cx+Ccθy˙θ2cy+Ccx˙x2c+Ccy˙y2c+Ccz+˙z2c)+1/2(Csθx˙θ2sx+Csθy˙θ2sy+Csx˙x2s+Csy˙y2s+Csz+˙z2s)+1/2N∑i=1(Cpiu˙θ2piu+Cpiv˙θ2piv+Cpiu˙δ2piu+Cpiv˙δ2piv+Cpiwδ2piw)+1/2(Crθx˙θ2rx+Crθy˙θ2ry+Crθz˙θ2rz+Crx˙x2r+Cry˙y2r+Crz˙z2r)+1/2(C2wθx˙θ22wx+C2wθy˙θ22wy+C2wx˙x22w+C2wy˙y22w+C2wz˙z22w)+1/2(C2pθx˙θ22px+C2pθy˙θ22py+C2px˙x22p+C2py˙y22p+C2pz˙z22p)+1/2(C3wθx˙θ23wx+C3wθy˙θ23wy+C3wx˙x23w+C3wy˙y23w+C3wz˙z23w)+1/2(C3pθx˙θ23px+C3pθy˙θ23py+C3px˙x23p+C3py˙y23p+C3pz˙z23p)+1/2(Cgθx˙θ2gx+Cgθy˙θ2gy+Cgθz˙θ2gz+Cgx˙x2g+Cgy˙y2g+Cgz˙z2g)+1/2(Cpθy˙θ2py+Cpx˙x2p+Cpz˙z2p)+1/2(Ctθy˙x2ty+Ctx˙x2t+Ctz˙z2t),
|
(11) |
|
R2pw=1/2⋅C2pw˙δ22pw,
|
(12) |
式中,Cspi为太阳行星齿轮啮合阻尼;˙δspi为太阳行星齿轮啮合线方向等效振动速度。Crpi为齿圈行星齿轮啮合阻尼;˙δrpi为齿圈行星齿轮啮合线方向等效振动速度。Cmθx为主轴x轴扭转向支撑阻尼。C2wp为中间级齿轮啮合阻尼;˙δ2wp为中间级齿轮啮合线方向等效振动速度。C3wp为高速级齿轮啮合阻尼;为高速级齿轮啮合线方向等效振动速度。
根据拉格朗日方程,定义拉格朗日算子L=T-U,对系统各自由度求偏微分
|
{ddt(∂L∂˙e)−∂L∂e+∂R∂˙e=Feddt(∂L∂˙f)−∂L∂f+∂R∂˙f=Ffddt(∂L∂˙g)−∂L∂g+∂R∂˙g=Fgddt(∂L∂˙h)−∂L∂h+∂R∂˙h=Fhddt(∂L∂˙l)−∂L∂l+∂R∂˙l=Fl,
|
(14) |
其中,e为传动主轴自由度,为6方向自由度;f为齿轮箱传动系统自由度,共66个自由度;g为齿轮箱箱体自由度,为6方向自由度;h为机舱自由度,为3方向自由度(x,z及θy);l为塔筒自由度,为3方向自由度(x,z及θy)。整理求导后系统各方向方程,可得基于柔性支撑的传动链耦合系统动力学方程
式中,M为系统质量矩阵,x(¨x,˙x)为系统振动位移(速度,加速度)矩阵;C为系统阻尼矩阵;K为系统刚度矩阵;F为系统外部载荷矩阵,其中发电机考虑为系统扭矩负载。
3 兆瓦级风电机组传动链动态特性分析
表 3、4所示为某3点支撑兆瓦级风电机组系统及齿轮箱参数。
表 3(Table 3)

表 3 风机基本工作参数
Table 3 Fundamental operating parameters of wind turbine
| 功率 |
叶片数目 |
启动风速 |
额定风速 |
切入风速 |
发电机效率 |
齿轮箱效率 |
齿轮箱传动比 |
发电机类型 |
安全风速 |
| 2 MW |
3 |
6.6 m/s |
10 m/s |
3 m/s |
≥97% |
≥97% |
115.25 |
异步双馈 |
26 m/s |
|
表 3 风机基本工作参数
Table 3 Fundamental operating parameters of wind turbine
|
表 4(Table 4)

表 4 齿轮箱基本参数
Table 4 Fundamental operating parameters of gearbox
| 参数 |
齿数 |
模数 |
压力角/(°) |
| 行星级 |
太阳轮 |
21 |
15 |
25 |
| 行星轮 |
37 |
15 |
25 |
| 内齿圈 |
96 |
15 |
25 |
| 中间级 |
主动轮 |
97 |
11 |
20 |
| 从动轮 |
23 |
11 |
20 |
| 高速级 |
主动轮 |
103 |
8 |
20 |
| 从动轮 |
21 |
8 |
20 |
|
表 4 齿轮箱基本参数
Table 4 Fundamental operating parameters of gearbox
|
忽略阻尼的影响,对上述方程求解,提取耦合系统前16阶固有频率如表 5所示。
表 5(Table 5)

表 5 传动链前16阶固有频率
Table 5 First 16 order natural frequencies of the drive train
| 阶次 |
1 |
2 |
3 |
4 |
| 频率/Hz |
1.69 |
35.5 |
36.6 |
54.2 |
| 阶次 |
5 |
6 |
7 |
8 |
| 频率/Hz |
113.7 |
115.1 |
116.7 |
266.3 |
| 阶次 |
9 |
10 |
11 |
12 |
| 频率/Hz |
329 |
333.2 |
564.1 |
1 017.2 |
| 阶次 |
13 |
14 |
15 |
16 |
| 频率/Hz |
1 019.47 |
1 020 |
1 264.4 |
1 950.9 |
|
表 5 传动链前16阶固有频率
Table 5 First 16 order natural frequencies of the drive train
|
由于主轴与齿轮箱各部件多为旋转部件,这些部件的转频或啮合频率均可能激发传动链的共振,对整个风机是潜在的威胁,需要对传动链进行潜在共振分析。表 6为传动链主要激励频率,包括各轴的转频以及各级啮合频率。
表 6(Table 6)

表 6 传动链内部激励频率
Table 6 Internal excitation frequencies of the drive train
| 项目 |
切入转速/(r·min-1) |
| 额定转速/(r·min-1) |
| 切出转速/(r·min-1) |
| 1050 |
1790 |
1900 |
| ms_1x |
0.152 |
| 0.258 |
| 0.275 |
| ms_2x |
0.304 |
| 0.512 |
| 0.545 |
| ms_3x |
0.455 |
| 0.776 |
| 0.824 |
| Ls_1x |
0.846 |
| 1.44 |
| 1.53 |
| Ls_2x |
1.69 |
| 2.88 |
| 3.06 |
| Ls_3x |
2.53 |
| 4.33 |
| 4.59 |
| is_1x |
3.57 |
| 6.08 |
| 6.46 |
| is_2x |
7.14 |
| 12.17 |
| 12.91 |
| is_3x |
10.7 |
| 18.25 |
| 19.37 |
| hs_1x |
17.5 |
| 29.83 |
| 31.67 |
| hs_2x |
35 |
| 59.67 |
| 63.3 |
| hs_3x |
52.5 |
| 89.5 |
| 95 |
| Lm_1x |
17.77 |
| 30.29 |
| 32.15 |
| Lm_2x |
35.5 |
| 60.57 |
| 64.30 |
| Lm_3x |
53.30 |
| 90.86 |
| 96.45 |
| im_1x |
82.06 |
| 139.9 |
| 148.5 |
| im_2x |
164.1 |
| 279.8 |
| 297 |
| im_3x |
246.2 |
| 419.7 |
| 445.5 |
| hm_1x |
402.5 |
| 686.2 |
| 728.3 |
| hm_2x |
735 |
| 1253 |
| 1330 |
| hm_3x |
1102.5 |
| 1879 |
| 1995 |
| 注:ms_kx主轴第k阶转频,Ls_kx低速轴第k阶转频,is_kx中间轴第k阶转频,hs_kx高速轴第k阶转频,Lm_kx低速级k倍啮合频率,im_kx中间级k倍啮合频率,hm_kx高速级k倍啮合频率(k=1~3) |
|
表 6 传动链内部激励频率
Table 6 Internal excitation frequencies of the drive train
|
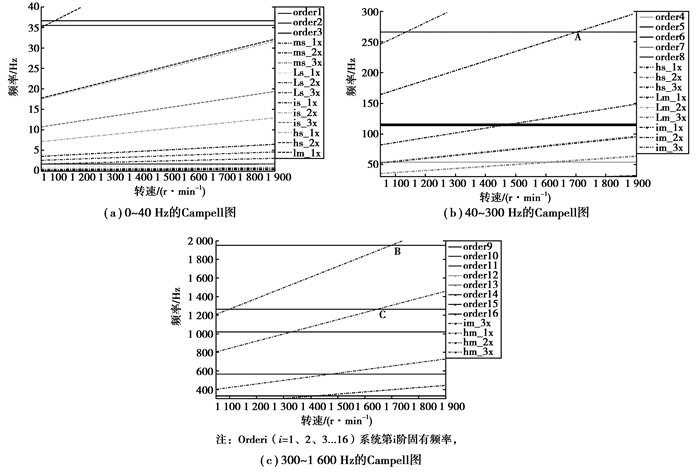
利用风电系统传动链固有频率与系统主要激励频率作Campell图,如图 5所示。从图中可以看出,在转速为1 700.9 r/min时存在共振点A,为中间级2倍啮合频率与第八阶系统固有频率266.3 Hz交点,额定转频裕度为5.03%;在转速为1 695 r/min时,存在共振点B,为高速级啮合频率3倍频与第十六阶固有频率1 950.9 Hz的交点,额定转频裕度为5.3%;在转速为1 649.4 r/min时存在共振点C,为高速级2倍啮合频率与第十五阶系统固有频率1 264.4 Hz交点,额定转频裕度为7.9%。其余共振点离额定转频较远。
为了验证分析模型的正确性,考虑塔筒支撑作用,采用Simpack建立了其柔性支撑传动链刚柔耦合多体动力学模型如图 6所示,得到系统前6阶固有频率如表 7所示,其对应振型如图 7所示。可以看出前面集中参数分析结果与有限元仿真结果基本一致,同时从图 7所示振型可以看出其第二阶固有频率为塔筒的摆动,第四阶固有频率为塔筒的摆动与齿轮箱行星架等转动部件的扭转相耦合。从图 5的(a)、(b)中可以看出,传动链第二阶固有频率和第四固有频率与部分转频存在交点,是风机传动链的潜在共振点,因此进一步证实了考虑塔筒扭摆的必要性。
表 7(Table 7)

表 7 传动链前6阶固有频率
Table 7 First 6 order natural frequencies of the drive train
| 阶次 |
1 |
2 |
3 |
4 |
5 |
6 |
| 频率/Hz |
1.69 |
35.4 |
36.4 |
55.7 |
113.3 |
115.8 |
|
表 7 传动链前6阶固有频率
Table 7 First 6 order natural frequencies of the drive train
|
4 结论
考虑风机塔筒的摆动与风机传动链的扭转耦合效应,采用集中参数法建立了基于柔性塔筒支撑的兆瓦级风电机组传动链耦合振动分析模型,并对传动链系统动态固有特性进行求解,利用Campell图对风机传动链潜在共振点进行了分析,得出切入转速与切出转速之间的潜在共振频率主要为:中间级2倍啮合频率与第八阶系统固有频率交点266.3 Hz,高速级啮合频率3倍频与第十六阶固有频率的交点1 950.9 Hz和高速级2倍啮合频率与第十五阶系统固有频率交点1 264.4 Hz,其余共振点离额定转频较远。利用Simpack建立了风机传动链多体系统动力学模型,仿真分析结果表明集中参数模型与有限元仿真结果基本一致,验证了分析方法的正确性。研究为风机传动链设计提供参考,具有重要的理论意义与工程应用价值。

 2015, Vol. 38
2015, Vol. 38


