2. 中船重工(重庆)海装风电设备有限公司,重庆 401122;
3. 重庆交通大学,重庆 400074
2. CSIC (Chongqing) HaizhuangWindpower Equipment Co., Ltd., Chongqing 401122, P.R.China;
3. Chongqing Jiaotong University, Chongqing 400074, P.R.China
目前风机制造行业载荷计算软件,如GH Bladed, Flex, Fast, HAWC2等普遍采用GL规范[1]所推荐的6个关键坐标系进行载荷的计算及输出。然而,随着风机向大型化和精确化发展,日益增加的降载设计需求、风机载荷测试、零部件寿命预测以及理论模型的试验验证均需要载荷在各坐标系之间进行转换以获取更接近真实值的载荷,但传统简单坐标系载荷结果已越来不能满足风电机组设计需求。
国内外学者已经对风机载荷进行了大量研究。Lackner[2]针对浮动风力发电机组及惯性引起的风机载荷,提出了一种新的逻辑控制方法,有效减小了浮动风力发电机组的载荷,延长了风机使用寿命;Dunne[3]采用风速预测的方法设计前馈控制系统用于减少风机的疲劳载荷,延长风机寿命;Vetas[4]公司设计一种载荷控制方法用于降低风机叶片载荷不平衡;Yao[5]在建立自由载荷控制模型的前提下, 采用独立变桨距控制, 实验结果表明这种控制策略在控制风机叶片载荷方面优于传统的统一变桨距控制策略;Larsen[6]、Bossanyi[7]等研究了独立变桨距的控制方法有效地控制风力发电组的载荷减少;孙磊[8]对大型风电机组的叶片载荷进行了大量建模仿真分析,获得了较准确的载荷结果,戴巨川等[9]对离心力引起的变桨距载荷、气动力引起的变桨距载荷、重力引起的变桨距载荷等进行系统研究;叶杭冶等[10]采用变桨距控制和转矩控制的并联控制的方法研究风机动力学问题,减小了风机载荷;应有等[11]则对风机机组的载荷优化进行了研究。这些研究为风机载荷的识别与优化提供了有效支撑,但目前对各个坐标系载荷的转换研究仍然较少。
文章探索风机坐标系的载荷转化分析模型,确定载荷转换的影响因素,对某5 MW海上风机的1 204种海上工况的载荷结果与GH Bladed软件的仿真结果进行对比验证,验证分析模型的可靠性。
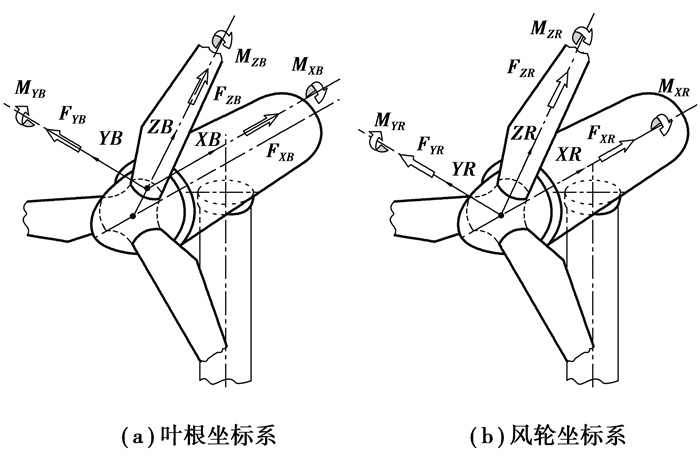
1 风电机组坐标系GH Bladed作为全球通用的风电机组载荷计算机性能仿真分析软件,采用GL规范所推荐的6大坐标系进行载荷结果输出。主要包括叶根坐标系、弦线坐标系、固定轮毂坐标系、风轮坐标系、偏航轴承坐标系、塔筒坐标系,各坐标系的详细定义见GL规范。文中重点使用叶根坐标系和风轮坐标系,见图 1所示。
|
图 1 叶根坐标系和风轮坐标系 Figure 1 Coordinate system of blade root and rotor |
图 1中:叶根坐标系原点位于叶片根部,x轴指向风轮轴线,z轴指向叶尖、y轴与xz轴符合右手规则。风轮坐标系原点位于风轮中心,x轴指向风轮轴线,z轴沿着叶片1、y轴与xz轴符合右手规则。
在各坐标系载荷之间的转换中,风轮坐标系和固定轮毂坐标系、塔筒各截面载荷的转化相对简单。叶片根部和风轮坐标系、风轮坐标系和塔顶坐标系之间的转化,有很多相通之处。文中以表 1所示的某5 MW海上风电机组为研究对象,重点分析叶片根部坐标系和风轮坐标系之间的载荷转化。
| 表 1 某5 MW海上风电机组参数 Table 1 Parameters of the 5 MW offshore wind turbine |
分别使用简单模型和改进模型,分析叶根坐标系和风轮坐标系之间推力的转化关系,并与GH Bladed软件结果进行对比分析和验证。
2.1 简单模型简单模型即通过常规的影响因素分析,进行各影响因素的公式计算。根据GL规范要求,叶尖距离塔筒的最小距离应大于30%的净空,对于千瓦级以上的风电机组,由于叶片较长及刚度影响,导致其变形量过大而使叶尖间隙不能满足规范要求,存在着与塔筒碰撞的危险。因此,常规的风电机组均考虑一定的主轴倾角和叶片锥角,以增大叶尖间隙。从叶根坐标系与风轮坐标系的定义可以看出,当考虑主轴倾角及叶片锥角后,叶根推力FXB与风轮推力FXR并不同向。因此,两者之间的转化需要考虑以下影响因素包括:叶片锥角φ;主轴倾角δ;风压对轮毂的阻力;机舱前后加速度和机舱俯仰旋转加速。
上述各因素的影响,可以分别用数学公式描述。
叶片锥角的影响为
| F=∑3i=1FXBi⋅cosφ−∑3i=1FZBi⋅sinφ, | (1) |
式中:FXBi为叶片i叶根坐标系的z向力;FZBi为叶片i叶根坐标系的z向力;φ为叶片安装角。
主轴倾角的影响为
| Fm=mhub⋅g⋅sin(δ+φy), | (2) |
式中:mhub为轮毂质量;g为重力加速度;δ为主轴倾角;φy为机舱俯仰角。
风压的影响为
| Fair=12ρ⋅s⋅V2⋅μ, | (3) |
式中:ρ为空气密度;s为轮毂罩受风面积;V为轮毂处平行于主轴的风速;μ为空气阻尼系数。
机舱前后加速度的影响为
| Fa=−mhub⋅ax⋅cos(δ+φy), | (4) |
式中:ax为机舱沿x轴的平移加速度。
机舱俯仰加速度的影响为
| Fτ=mhub⋅(az−l⋅a′y)⋅sin(φy+φ), | (5) |
式中:l为风轮坐标系原点到塔顶坐标系原点的距离;az为机舱沿z轴的平移加速度;a′y为机舱绕y轴的旋转加速度;φ为l与水平面的夹角。
综合考虑式(1)~(5)所示的各载荷值后,推算出的风轮推力为
| FXR=F+Fm+Fair+Fa+Fτ. | (6) |
使用GH Bladed软件建立上述机组的载荷分析模型,对GL2005规范所定义的1 204种海上风电机组设计工况进行载荷计算,形成一套完整工况的载荷数据库。使用工况载荷数据库中的叶根载荷,结合上述建模方法,推算出1 204种工况下的风轮坐标系载荷,可获得公式1~6中的各影响因素F、Fm、Fair、Fa、Fτ的值,并对比FXR、F′XR(是指公式6中去掉Fair所得的推力载荷)以及GH Bladed软件计算所得的风轮坐标系的推力值Rotating hub Fx,对比结果见表 2所示,单位均为kN。
| 表 2 各分量极限值 Table 2 Extreme loads for every component |
计算结果表明,当考虑风压时,使用简单模型所得的载荷结果与GH Bladed软件所得结果的偏差小于5%;而当不考虑风压时,使用简单模型所得的载荷结果与GH Bladed软件所得结果的偏差小于0.3%。因此表明在GH Bladed 4.2版本中,没有考虑轮毂罩处的风压载荷。
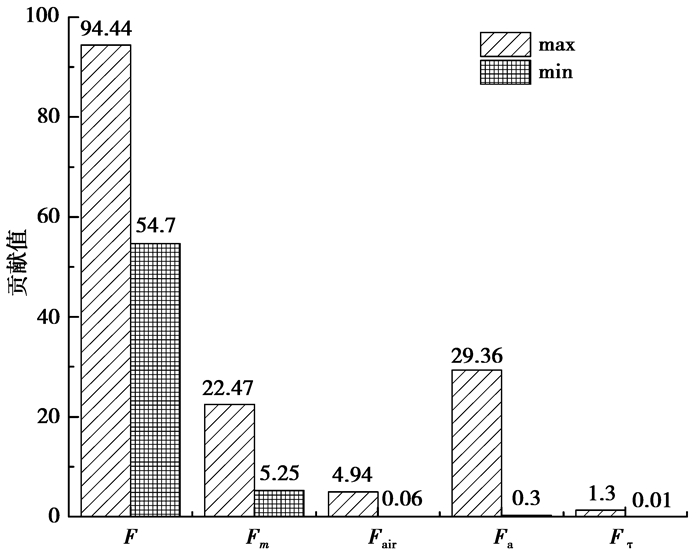
根据表 2的分析结果可得到风轮坐标系推力的各组成分量的贡献大小,如图 2所示。
|
图 2 各分量的最大最小贡献 Figure 2 Max and min contribution of every component |
从图 2可以看出,风轮系统的推力55%~94%来自于叶根载荷,并受叶片锥角的影响;5%~22%来自于主轴倾角,并受轮毂重量的影响;0.06%~5%来自于轮毂罩的风压,并受轮毂罩面积和气压的影响;0.3%~30%来自于机舱前后平移加速度;0~1.3%来自于机舱俯仰加速度。这些细分的载荷组成数据可为机组特定工况降载提供重要的数据支撑。
2.2 改进模型为完整体现机组的实际受载情况,结合坐标转换关系,在简单模型基础上提出二维和三维改进模型。
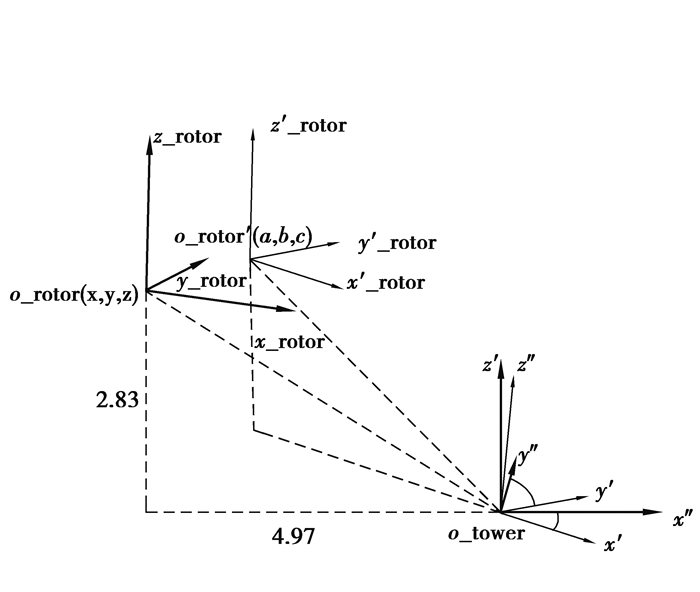
建立风轮坐标系xyzo,当风轮坐标系xyzo分别绕z、y、x轴旋转角度φx, φy, φz后,分别获得x′y′z′o′坐标系、x″y″z″o坐标系、(a,b,c)矢量。示意图见图 3所示,相应的载荷转化关系见式(7)~(9)。
|
图 3 风轮和塔顶坐标系示意图 Figure 3 Coordinate system of rotor relative to tower top |
| {x′=x⋅cosφz−y⋅sinφz,y′=x⋅sinφz+y⋅cosφz,z′=z | (7) |
| {x″=x′⋅cosφy+z′⋅sinφy,y″=y′,z″=−x′⋅sinφy+z′.cosφy, | (8) |
| {a=x″,b=−(y″⋅cosφx+z″sinφx),c=−y″.sinφx+z″⋅cosφx). | (9) |
式中,φx, φy, φz为机舱绕x,y,z方向的旋转角度。
因主轴有6°倾角,故其方向向量坐标为(cos174°,0,sin174°),经φx, φy, φz旋转后(见公式7~9),可得旋转后的方向向量(A,B,C)。
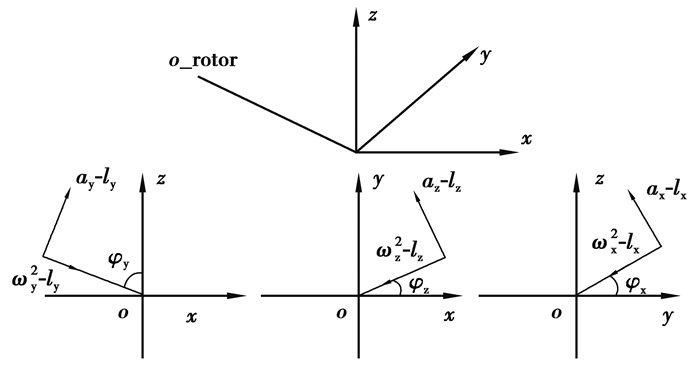
轮毂质心是风轮坐标系中固定的点,因此轮毂质心保持与风轮坐标系相一致的运动状态。风轮坐标系旋转产生的向心加速度和切向加速度,其矢量分解如图 4所示。相应得到其绝对坐标系的加速度axD3, ayD3, azD3为
| {axDs′=ax+ω2ylycos(29.6∘+φy)+a′ylysin(29.6∘+φy)−ω2zlzcosφz−a′zlzsinφz,ayD′3=ay−ω2zlzsinφz+a′zlzcosφz−ω2xlxcosφx−a′xlxsinφx,azD3′=az−ω2ylysin(29.6∘+φy)+a′ylycos(29.6∘+φy)−ω2xlxsinφx+a′xlxcosφx, | (10) |
其中:ax,ay,az分别为机舱沿x、y、z轴的平移加速度;ωx, ωy, ωz分别为机舱绕x、y、z轴的旋转速度;a′x, a′y, a′z分别为机舱绕x、y、z轴的旋转加速度;lx, ly, lz分别为风轮坐标系原点到塔顶坐标系x、y、z轴的距离。
|
图 4 轮毂质心的加速度示意图 Figure 4 Decomposed acceleration of hub mass centre |
主轴系统如图 5所示,主轴方向的重力如式(11)所示。考虑叶片有4°锥角,3个叶根的力转化为风轮坐标系后的方程如式(12)表示。三维改进模型中的风轮推力则如式(13)所示。
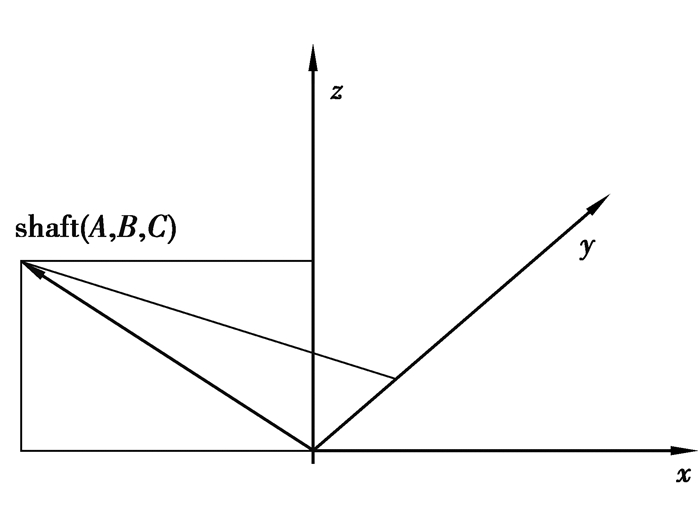
|
图 5 主轴系统 Figure 5 Main shaft system |
当只考虑x-z平面运动,且不考虑由机舱角速度引起的向心加速度情况时,将风轮推力三维改进模型简化为二维改进模型,如式(14)~(16)所示, 其中,axD′2, azD′2, Fxa, Fza分别为x、y方向的加速度分量和x、y方向质量力。
以上述5 MW海上风电机组为例,对1 204种载荷工况,分别使用简化模型、三维改进模型、二维改进模型进行载荷推导,对各种计算方法所得结果进行差值对比(如表 3所示)。用字母Sp、D3、D2、B分别代表简化模型、三维改进模型、二维改进模型和GH Bladed模型计算。而Sp-B即以Sp方法计算结果减去B所得结果,此行基准值代表GH Bladed值。
| Fa,g=−mhub−axD′3A−ayD′3B−(azD′3+g).C√A2+B2+C2, | (11) |
| F=(FXB1+FXB2+FXB3)⋅cos4∘−(FZB1+FZB2+FZB3)⋅sin4∘, | (12) |
| FXR3=Fa,g+F, | (13) |
| {axD′2=ax+ω2ylycos(29.6∘+φy)+a′ylysin(29.6∘+φy),azD′2=az−ω2ylysin(29.6∘+φy)+a′ylycos(29.6∘+φy), | (14) |
| {Fxa=−mhub⋅ax2′.cos(φy+6∘),Fza=mhub⋅(az2′+g)⋅sin(φy+6∘), | (15) |
| FXR2=Fxa+Fza+F, | (16) |
| 表 3 载荷差值表 Table 3 Load derivations between two methods |
由表 3可见:简化模型所得结果与GH Bladed的偏差为0.292%;三维改进模型所得结果与GH Bladed软件结果偏差为0.356%;当三维改进模型仅考虑x-z平面运动,转化为二维改进模型,二维改进模型与GH Bladed偏差在0.081%之内。由此可见,Bladed所考虑模型并不是最精确的三维模型。
3 力矩分析在力坐标系转换基础上,进行力矩分析。把叶根力矩转化为轮毂力矩,需要考虑:叶片锥角、风轮转速的变化、机舱x方向的角加速度、轮毂偏向(轮毂质心与风轮坐标系原点重合时,加速度不会对弯矩产生影响)和陀螺力矩(因陀螺力矩对载荷影响很小,暂不考虑)。
将xyzo坐标系绕y轴旋转至z轴与shaft平行(变为x′y′z′o′),再将x′y′z′o′平移到x″y″z″o,见示意图 6,相应的载荷转化关系见式(17)。
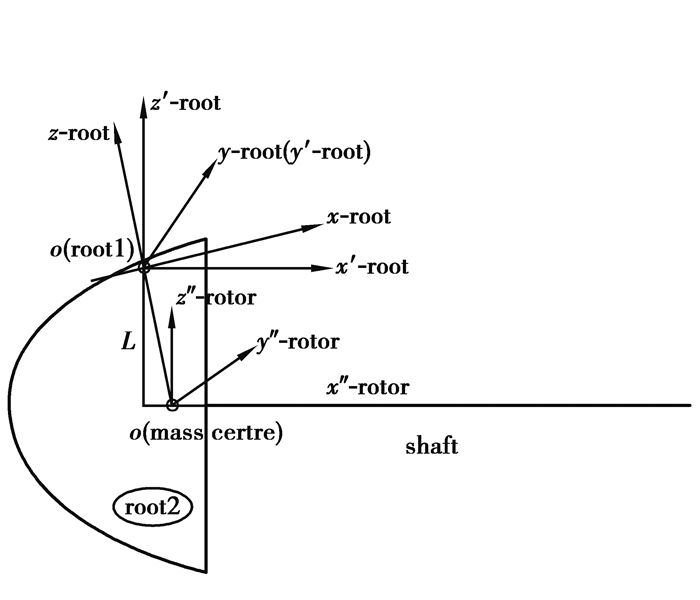
|
图 6 叶根坐标系转化示意图 Figure 6 Transform diagram for blade root coordinate systems |
x方向角加速度见式(18),其中:nrotor为风轮转速;Jrotor为轮毂相对于主轴的转动惯量。因为绕z轴的扭转加速度极小,倾角也较小,故在计算中做省略处理,对结果基本没有影响。三叶片合成见式(19)。
| {M″xi=Mxi⋅cos4∘−Mzi⋅sin4∘−Fyi⋅L,M″yi=Myi+L⋅(Fxi⋅cos4∘)−L⋅tan4∘⋅(Fxi⋅sin3.5∘+Fzu⋅cos4∘),M″zi=Mxi⋅sin4∘+Mzi⋅cos4∘−L⋅Dyi⋅tan4∘, | (17) |
| Fa=−(dnrotordt+a′y⋅cos(φy+δ)−a′z⋅sin(φy+δ))⋅Jrotor, | (18) |
| {∑Mx=M″x1+M″x2+M″x3+Fa,∑My=M″y1−(M″y2+M″y3)⋅cos60∘+(M″z3−M″z2)⋅sin60∘,∑Mz=M″z1−(M″z2+M″z3)⋅cos60∘+(M″z2−M″z3)⋅sin60∘. | (19) |
对上述5 MW海上风电机组进行1 204种载荷工况力矩分析,获取Mx、My、Mz绝对偏差最大的3个工况,并与GH Bladed 4.2所得结果进行比较,如图 7所示。由图 7可见,Mx的最大偏差小于1.4%,My的最大偏差小于1%,Mz的最大偏差小于1.1%,整体拟合较为准确。
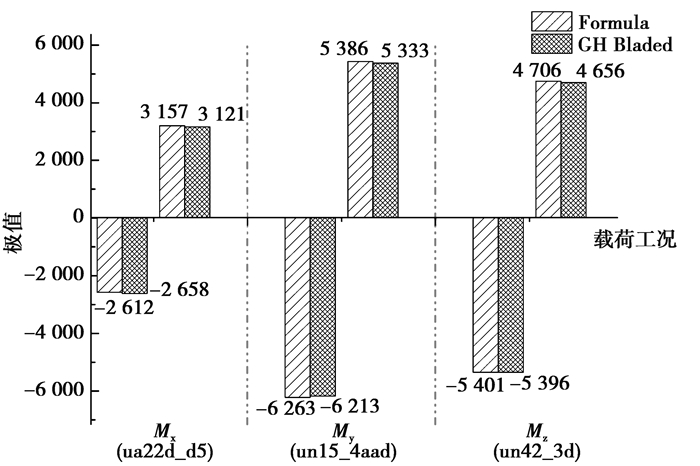
|
图 7 偏差最大工况的弯矩极值 Figure 7 Values from formula and GH Bladed when maximum derivation occurs |
根据风电机组受载特点,提出把叶根坐标系载荷转化为风轮坐标系载荷的建模方法,通过与GH Bladed软件所得结果的对比,确定分析模型的正确性;并进一步使用空间矢量理论,大胆提出更接近实际情况的二维和三维改进模型。研究结果表明:
1) 当未考虑风压载荷时,使用简化模型所计算的推力与GH Bladed软件计算结果的偏差小于0.3%,力矩结果偏差小于1.4%;当考虑风压载荷时,计算的推力与GH Bladed软件所得结果的偏差小于5%。故GH Bladed 4.2软件计算风轮推力时,并未考虑轮毂罩的风压影响。
2) 未考虑风压影响时,三维改进模型所得推力与GH Bladed软件结果偏差在0.356%;当三维改进模型仅考虑x-z平面运动,转化为二维模型时,二维模型所得推力与GH Bladed结果偏差在0.081%之内。因此GH Bladed 4.2软件并不是最精确的三维模型。
| [1] | Germanischer lioyd industrial services gmbll.2010-R0 Guideline for the certification of wind turbines edition[S].Germany, Germanischer Lloyd, 2010. |
| [2] | Lackner M A. An investigation of variable power collective pitch control for load mitigation of floating offshore wind turbines[J]. Wind Energy, 2013, 16(3): 435–444. DOI:10.1002/we.v16.3 |
| [3] | Dunne F, Simley E, Pao L Y.LIDAR wind speed measurement analysis and feed-forward blade pitch control for load mitigation in wind turbines[R].Colorado:University of Colorado Boulder, 2011. |
| [4] | Lars R, Rasmus S, Carl M E.Wind turbine with pitch control arranged to reduce life shortening loads on components there of:United States, 8096762[P].2012-01-17. |
| [5] | Yao Xingjia, Wang Xiaodong, Xing Zuoxia, et al.Individual pitch control for variable speed turbine blade loads mitigation[C]//Proceedings of IEEE International Conference on Sustainable Energy Technologies Nov24-27, 2008, Singapore.Piscataway:IEEE Press, 2008:769-772. |
| [6] | Larsen T J, Madsen H A, Thomsen K. Active loads reduction using individual pitch based on local blade flow measurements[J]. Wind Energy, 2005, 8(1): 67–80. DOI:10.1002/(ISSN)1099-1824 |
| [7] | Bossanyi E A. Further loads reductions with individual pitch control[J]. Wind Energy, 2005, 8(4): 481–485. DOI:10.1002/(ISSN)1099-1824 |
| [8] | 孙磊.大型风力发电机组风轮载荷的仿真计算与控制[D].沈阳:沈阳工业大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10142-2009099076.htm |
| [9] |
戴巨川, 胡燕平, 刘德顺, 等.
大型风电机组变桨距载荷计算与特性分析[J]. 中国科学:技术科学, 2010, 40(7): 778–785.
DAI Juchuan, HU Yanping, LIU Shunde, et al. Calculation and characteristics analysis of blade pitch loads for large scale wind turbines[J]. Scientia Sinica: Technologica, 2010, 40(7): 778–785. (in Chinese) |
| [10] |
叶杭冶, 潘东浩.
风电机组变速与变桨距控制过程中的动力学问题研究[J]. 太阳能学报, 2007, 28(12): 1321–1328.
YE Hangye, FAN Donghao. Dynamic analysis of variable speed and pitch controlled wind turbines[J]. Acta Energiae Solaris Sinica, 2007, 28(12): 1321–1328. (in Chinese) |
| [11] |
应有, 许国东.
基于载荷优化的风电机组变桨控制技术研究[J]. 机械工程学报, 2011, 47(16): 106–119.
YING You, XU Guodong. Development of pitch control for load reduction on wind turbines[J]. Journal of Mechanical Engineering, 2011, 47(16): 106–119. DOI:10.3901/JME.2011.16.106 (in Chinese) |
 2015, Vol. 38
2015, Vol. 38


