在实际运行环境中,由于风速的随机性、湍流、风剪和塔影效应等不稳定因素的影响,风轮平面内会产生不均衡载荷,而且随着风力发电机组的大型化,这种不均衡载荷影响变得越来越大。现代大型风力发电机控制技术不但要解决风能最大功率跟踪和电能质量控制两大关键问题,还要解决风机主要部件受载等问题,对风力发电机进行减振控制,以延长风力机的运行寿命。
独立变桨控制技术是近年来在统一变桨技术上发展起来的一种风力发电控制技术,其优点在于通过降低风轮平面内的不均衡载荷,从而减少轮毂、主轴、塔架等一系列关键部件的振动。文献[1]使用的周期变桨控制可有效减轻一阶旋转频率引起的载荷。文献[2]引入状态空间方法来抵消风剪导致的载荷。文献[3-4]通过测量获得叶根载荷的平均值,将其解耦到2个相互垂直的坐标系上,这样就能使用传统的单输入单输出控制方法,国内外对风力机独立变桨控制已经进行了相应研究[5-8]。
文中分析了风剪和塔影效应,在此基础之上提出了独立变桨控制策略。将独立变桨控制下的仿真结果与统一变桨比较发现,通过独立变桨可以有效降低风力发电机的振动载荷,达到了较好的减振目的。采用联合仿真技术,在Simulink中进行控制设计,将得到的控制信号返回FAST进行风机的非线性仿真[9],同时引入干扰自适应控制技术,以此抑制或者减小风速、湍流、风剪和塔影效应等对风力发电机的影响,提高了系统鲁棒性。
1 风特性分析风模型主要分为3种:常风、湍流风和阵风模型。其中,湍流风[10]是指风向和大小都随时间变化的风,是常见的风模型之一。除了以上3种风模型外,实际情况下,还要考虑风剪切、塔影效应等因素对风电机组的影响。
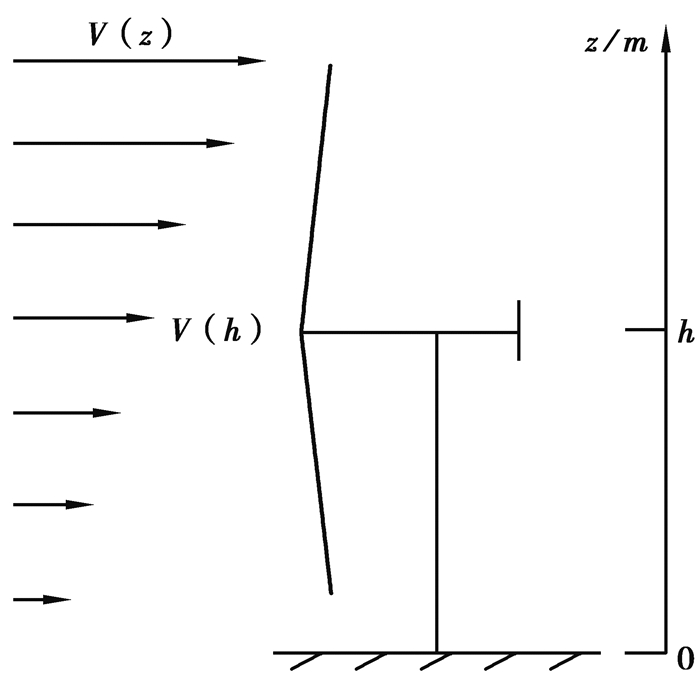
1.1 风剪切效应自然风是随机变化,分布不均匀的。风速的变化受高度的影响很大,而且随着风力机组的大型化,这种影响越明显。风剪切使得风速在竖直方向上发生了较大变化。风剪是指在竖直高度上风速的大小会随高度的不同发生变化,如图 1所示。设地面处的风速为零,则不同高度处的风速大小满足以下指数模型公式
| $ \frac{{V\left( z \right)}}{{{V_{\rm{h}}}}} = {\left( {\frac{z}{h}} \right)^\alpha }, $ | (1) |
|
图 1 风速随高度的变化 Figure 1 Wind speed vrition long height |
式中:z为离地垂直高度;V(z)为离地高度为处的风速;Vh为轮毂处风速;h为轮毂离地高度;α为风剪系数,它与大气稳定度和地面粗糙度有关,α值越大表示风速随高度变化明显。
1.2 塔影效应塔架干扰气流的分布,使空气流速度发生变化的现象称为塔影效应。塔影效应是风力发电过程中的一种负面效应,其结果会导致风机载荷波动,使发电机性能降低。在上风向风力发电机中,塔影效应可通过干扰控制技术来抑制或者抵消。上风向水平轴风力机风轮平面内的风速模型表达式为[11]
| $ V\left( {x,y} \right) = {V_h} + {V_0}{R^2}\left( h \right)\frac{{{y^2} - {x^2}}}{{{{\left( {{x^2} + {y^2}} \right)}^2}}}, $ | (2) |
式中:V0为平均风速;R(h)为高度h处的塔筒半径;y为叶片微元到塔架轴线在y方向的距离;x为桨叶微元到塔架轴线在x方向的距离。
2 独立变桨控制器设计 2.1 控制策略概述根据桨叶的变桨动作是否同步同量,变桨距控制分为统一变桨距控制(collective pitch control,CPC)和独立变桨距控制(individul pitch control,IPC)。统一变桨距控制所有叶片的桨距角变化完全相同,它是以轮毂高度处的风速或平均风速作为计算风速。由于风切和塔影效应会造成风轮平面内风速分布不均匀,而且叶片旋转时会受到轴向气动力作用,导致叶片产生拍打变形和轴向挥舞振荡[12],从而引起疲劳等问题。因此,以单一风速作为控制变量进行控制显然不够准确。
独立变桨距控制的各桨叶桨距角变化一般不同。相对于统一变桨,独立变桨可以有效地解决由于风切效应、塔影效应等扰动因素引起的桨叶、轴承和塔架等部件的载荷不均匀问题,从而减少变形和疲劳损害,稳定输出功率。独立变桨控制是指当风速高于额定风速时,各叶片开始进行独立地变桨距控制,并根据自身控制特点独立地动作,以此实现稳定输出功率在额定值附近的目的,这种变桨控制在一定程度上也解决了风力机主要部件载荷不均匀问题。
2.2 独立变桨控制器设计统一变桨控制是假定发电机功率始终维持在额定功率,对电机转矩实行恒转矩控制,由于风速的波动,使得转矩不稳定。为了改善风电机组的动力特性,降低转矩的波动,文中采用LQR (liner qudrtic regultor)控制方法。LQR用状态空间来模拟控制对象,通过全状态反馈,实现控制系统的多目标最优控制[13]。文中选取输入量为桨距角误差,转矩的变化量为状态变量,通过LQR最优控制减小转矩波动,从而提高发电机组的运行寿命。将风轮运动方程写成标准控制方程,即状态空间描述形式:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{\dot x}}\left( t \right) = \mathit{\boldsymbol{Ax}}\left( t \right) + \mathit{\boldsymbol{Bu}}\left( t \right)\\ \mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{Cx}}\left( t \right) + \mathit{\boldsymbol{Du}}\left( t \right) \end{array} \right\}。 $ | (3) |
目标函数为
| $ J = \int_0^\infty {\left( {\delta \mathit{\boldsymbol{x}}{{\left( t \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( t \right)\delta \mathit{\boldsymbol{x}}\left( t \right) + \delta \mathit{\boldsymbol{u}}{{\left( t \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}\left( t \right)\delta \mathit{\boldsymbol{u}}\left( t \right)} \right)} {\rm{d}}t $ | (4) |
式中:δx(t)为系统状态;δu(t)为控制输入;Q(t)为状态权重矩阵;R(t)为输入权重矩阵。
最优控制信号u(t)表达式为
| $ \mathit{\boldsymbol{u}}\left( t \right) = \mathit{\boldsymbol{Gx}}\left( t \right)。 $ | (5) |
式中:G为反馈增益矩阵,它是在系统的全状态反馈下计算的,在工程应用上并不经济,须引入状态观测器来估计状态变量的值。闭环状态观测器的数学模型为
| $ \mathop {\mathit{\boldsymbol{\hat x}}}\limits^. \left( t \right) = \left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{GC}}} \right)\mathit{\boldsymbol{\hat x}}\left( t \right) + \mathit{\boldsymbol{Bu}}\left( t \right) + \mathit{\boldsymbol{Gy}}\left( t \right) $ | (6) |
式中,
由于湍流和塔影效应等干扰因素会对风电机组产生额外载荷,从而导致零部件的振动。为了抑制或者抵消这些干扰,引入干扰自适应控制技术,构建自适应控制系统。DAC (disturbnce ccommodting control)是一种用来降低或抵消持续干扰的方法,基本思想是在状态观测器中引入干扰状态,将重构的干扰状态引入反馈增益中以抵消干扰输入的影响。干扰模型假定为以下的状态空间形式
| $ \left. \begin{array}{l} {{\dot z}_D}\left( t \right) = \mathit{\boldsymbol{F}}{z_D}\left( t \right)\\ {u_D}\left( t \right) = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}{z_D}\left( t \right) \end{array} \right\}, $ | (7) |
式中:F和Θ是已知的干扰状态矩阵和扰动输入矩阵;uD(t)为扰动输入;zD(t)为干扰状态。将干扰模型引入状态观测器模型中,得到带干扰的系统状态观测器模型,其表示为
| $ \mathop {\mathit{\boldsymbol{\hat x}}}\limits^. \left( t \right) = \left( {\mathit{\boldsymbol{A}} - {\mathit{\boldsymbol{G}}_x}\mathit{\boldsymbol{C}}} \right)\mathit{\boldsymbol{\hat x}}\left( t \right) + \mathit{\boldsymbol{Bu}}\left( t \right) + \Gamma {{\hat u}_d}\left( t \right) + \mathit{\boldsymbol{Gy}}\left( t \right)。 $ | (8) |
相应地,干扰状态观测器可表示为
| $ \left. \begin{array}{c} {{\dot z}_D}\left( t \right) = \mathit{\boldsymbol{F}}{z_D}\left( t \right) + {\mathit{\boldsymbol{G}}_d}\left( {y\left( t \right) - \hat y\left( t \right)} \right)\\ {u_D}\left( t \right) = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}{z_D}\left( t \right) \end{array} \right\}。 $ | (9) |
则状态方程的估计误差为
| $ \dot e\left( t \right) = \left( {\mathit{\boldsymbol{\overline A}} - \overline {\mathit{\boldsymbol{GC}}} } \right)e\left( t \right), $ | (10) |
其中:
由控制理论可知,只要(A, C)可观测,调节增益矩阵的增益系数,可配置(A-GC)的极点[14]在期望的极点附近,即可将极点配置到复平面虚轴的左侧,使得误差迅速衰减,使状态估计值能很好地跟踪系统状态。此时,反馈控制的全状态控制器则为
| $ \mathit{\boldsymbol{u}}\left( t \right) = \mathit{\boldsymbol{Gx}}\left( t \right) + {\mathit{\boldsymbol{G}}_d}{z_d}\left( t \right), $ | (11) |
将式(11)带入状态方程式(3)中得
| $ \mathit{\boldsymbol{\dot x}}\left( t \right) = \left( {\mathit{\boldsymbol{A + BG}}} \right)\mathit{\boldsymbol{x}}\left( t \right) + \left( {\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{G}}_d} + \Gamma \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right){z_d}\left( t \right)。 $ | (12) |
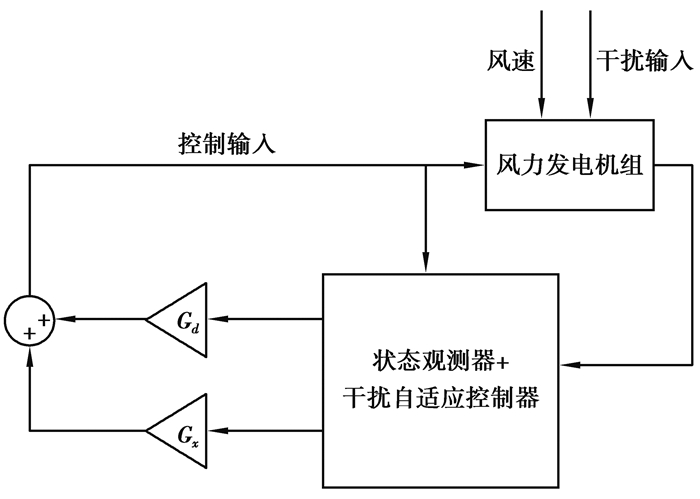
由式(12)可知,要消除扰动带来的干扰,即确定干扰反馈增益Gd,使‖BGd+ΓΘ‖尽量小。通过观测器估计叶尖变形,重构出干扰风速,这个干扰风速等同于塔影,湍流等因素共同作用的效果。控制算法抑制了叶尖变形就等效地降低了塔影,湍流等因素的影响。采用的状态观测器和干扰自适应控制结构框图如图 2所示。
|
图 2 状态观测器与干扰自适应控制的控制框图 Figure 2 Control digrm of state estimtor nd DAC |
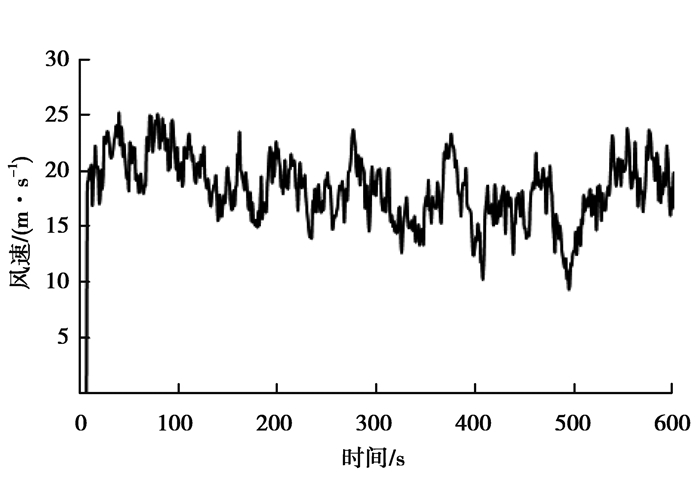
实例采用5 MW上风向风力发电机,机组主要技术参数为:额定功率为5 MW,叶片长度61.5 m,风轮直径为80 m,塔基和塔顶直径分别为6 m和3.87 m,轮毂直径为1.5 m,额定风速为11.5 m/s,切入风速为4 m/s,切出风速为25 m/s,风轮额定转速为12.1 r/min,发电机额定转矩为43 093.55 N·m,发电机额定转速为1 173.7 r/min。外部运行工况环境选择平均风速为18 m/s的湍流风,如图 3所示,因为在湍流风工况下风电机组性能和载荷情况最能反映一个控制器的好坏。
|
图 3 平均风速为18 m/s的湍流风曲线 Figure 3 The wind turbulence curve of 18 m/s verge wind speed |
采用美国可再生能源实验室开发的FAST软件与Mtlb/Simulink进行联合仿真,在Simulink中进行风机控制,并将得到的控制信号返回FAST中进行风机的非线性仿真控制。选择线性化点,通过FAST软件进行线性化生成线性化输出文件,提取出风力机模型的状态空间矩阵A,B。对矩阵A进行特征值分析可得系统的开环极点位置。第一对极点对应传动链一阶扭转模态,最后一个极点对应电机转速状态。
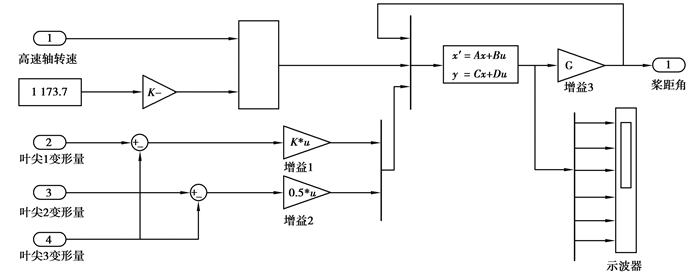
矩阵Q的选取采用试测法。通过不断调整Q值直到获得期望的闭环极点。比较闭环极点值和开环极点值,验证正确性。根据矩阵A, B, Q, R,通过Mtlb求得反馈矩阵G。使用LQR技术和DAC技术在Simulink中进行控制系统设计。图 4是状态空间控制子模型。
|
图 4 状态空间控制模型 Figure 4 State space control model |
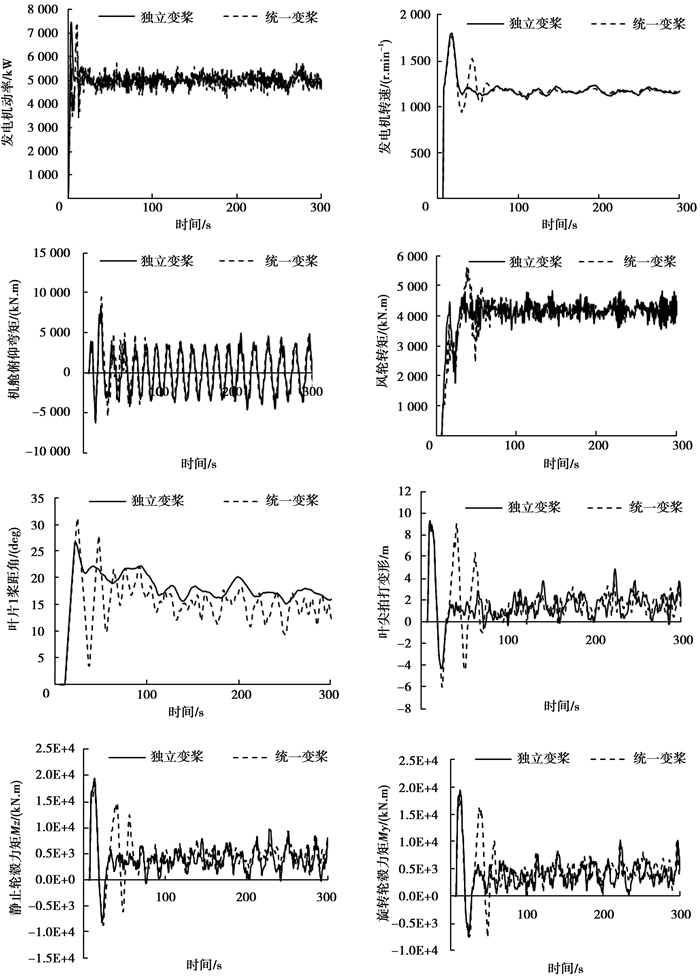
将5 MW风力发电机分别进行统一变桨和独立变桨控制仿真计算。文中仅列出了叶尖、轮毂和机舱部分数据,对比独立变桨和统一变桨下的变形、力矩等数据,计算结果见图 5。分析可知,采用LQR的独立变桨控制有效降低了叶尖拍打变形、叶根和轮毂处的载荷,相应地,其后续零部件如轮毂、主轴、塔架偏航轴承等的载荷均会有明显的降低。发电机功率和转矩也比较稳定。
|
图 5 独立变桨与统一变桨仿真结果比较 Figure 5 Simulation results compare of between ipc nd cpc |
从图 5结果可以得出,统一变桨的变桨频率度明显大于独立变桨控制的变桨频率,这对叶片的疲劳寿命有直接影响;在整个仿真过程中,使用独立变桨控制,电机转速要比统一变桨时稳定,波动较少,相应的振动影响会得到降低。由于本例采用恒定转矩控制,因此,发电机功率也比统一变桨控制时稳定;功率的剧烈变化会导致转子电流发生剧烈波动,当其超过变频器的额定值时会对电网造成破坏。
分析图 5还可知,独立变桨下载荷平均值虽然和统一变桨下的平均值相差不大,但是载荷波动幅值比统一变桨情况下要小很多,这表明在独立变桨情况下桨距角随风速变化实时调整,使得风力机的受载相对统一变桨要稳定。从计算结果来看,风力机各项振动值均有不同程度地降低,表明独立变桨可以有效降低风力发电机的载荷,延长风力机运行寿命。
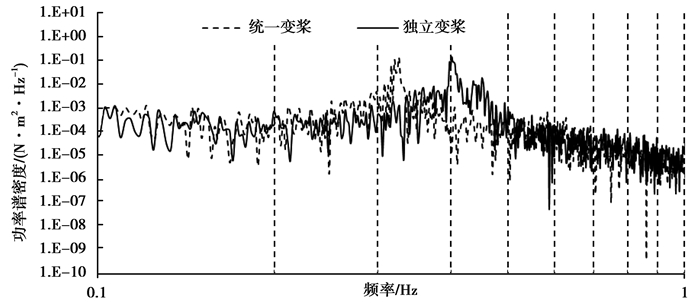
功率谱密度是评价随机振动的有效工具,其实质是把对时间域的振动描述转化为频率域的振动描述,从总体上来研究振动统计规律。随机过程的功率谱密度,反映了随机过程统计参量均方值在频率域上的分布,即在各个频率域上振动能量的概率分布。可以从功率谱密度中读出具有不同固有频率的振动能量的平均密度,从而避免或减小振动破坏。图 6为叶片拍打弯矩功率谱,可以看出,独立变桨有效地减小了风轮旋转频率分量的能量,因此与风轮旋转频率有关的载荷均会有较大的降低。
|
图 6 叶片拍打弯矩功率谱 Figure 6 Power spectrum of falp blade rotor bending moment |
表 1为等效疲劳载荷部分结果,可以看出,与统一变桨相比,独立变桨显著地降低了叶根、轮毂以及偏航轴承的载荷,其中以偏航轴承My减小最多。
| 表 1 等效疲劳载荷对比 Table 1 Comparison of equivalent fatigue load |
1) 采用联合仿真技术,结合LQR控制方法,对某兆瓦级风力发电机进行分析。分析表明LQR控制能有效地降低风轮平面内的不平衡载荷,从而减小了叶尖拍打变形和风力发电机关键零部件疲劳载荷,延长风力发电机组的使用寿命。
2) 干扰自适应控制技术的引入很大程度上消除了塔影、湍流变化等因素的影响,减少了风轮平面的不平衡载荷,震颤和剪切,系统具有良好的鲁棒性。
3) 独立变桨要求桨距角变化更加频繁,增大了变桨执行器的疲劳载荷。同时也相应的增加了执行结构的复杂性,这点是在工程实际中必须加以考虑和避免。
| [1] | Juul L T, Madson H A, Kenneth T. Active load reduction using individual pitch, based on local blade flow measurements[J]. Wind Energy, 2005, 8(1): 67–80. DOI:10.1002/(ISSN)1099-1824 |
| [2] | Wright A D.Modern control design for flexible wind turbines[R].US:midwest research institute battelle, 2004. |
| [3] | Bossanyi E A. Individual blade pitch control for load reduction[J]. Wind Energy, 2003, 6(2): 119–128. DOI:10.1002/(ISSN)1099-1824 |
| [4] | Bossanyi E A. Wind turbine control for load reduction[J]. Wind Energy, 2003, 6(3): 229–244. DOI:10.1002/(ISSN)1099-1824 |
| [5] | Wright A D.Modern Control design for flexible wind trubine[R].Washington:NREL, 2004. |
| [6] | John A, Vikram P. Control of flapwise vibrations in wind trubine blades using semi-active tuned mass dampers[J]. Struct Control Health Monit, 2011, 18: 840–851. DOI:10.1002/stc.v18.8 |
| [7] | Selvam K. Individual pitch control for large scale wind turbines[M]. The Netherlands: ECN, 2007. |
| [8] | Hu Y, Liu Y, Yao X J, et al. Multi-stageweight number individual variable-pitch control of mega-watt class wind turbine system[J]. Journal of shengyang university of Technology, 2009, 31(6): 633–638. |
| [9] | Jonkman J M, Buhl M L."Fast user's guide" golden[R].US:national renewable energy laboratory, 2005. |
| [10] |
何伟, 田德, 邓英, 等.
风力发电机组旋转湍流风场数值模拟[J]. 中国电机工程学报, 2013, 33(11): 82–87.
HE Wei, TIAN De, DENG Yin, et al. Turbulent wind field simulation of wind turbines with rotationals effects[J]. Proceedings of the CSEE, 2013, 33(11): 82–87. (in Chinese) |
| [11] |
孔屹刚, 王杰, 顾浩, 等.
基于风剪切和塔影效应的大型风力机独立变桨控制研究[J]. 华东电力, 2011, 39(4): 640–645.
KONG Yigang, WANG Jie, GU Hao, et al. Research on Individual Pitch Control Based on Wind Shear and Tower Shadow for Large Wind Turbine[J]. East China Electric Power, 2011, 39(4): 640–645. (in Chinese) |
| [12] |
何玉林, 苏东旭, 黄帅, 等.
变速变桨风力发电机组的桨距控制及载荷优化[J]. 电力系统保护与控制, 2011, 39(16): 95–100.
HE Yulin, SU Dongxu, HUANG Shuai, et al. Pitch control and load optimization of variable speed variable pitch wind turbine[J]. Power System Protection and Control, 2011, 39(16): 95–100. (in Chinese) |
| [13] | Tore Bakka, Hamid R K, Neil A D.Gain scheduling for output h∞control of offshore wind turbine[C]//Proceedings of the twenty-second (2012) international offshore and polar engineering conference rhodes, June 17-22, 2012, Greece, 2012. |
| [14] | Wang H Q, Cao D Q, Wang X D. The stochastic sliding mode variable structure guidance laws based on optimal control theory[J]. Journal of Control Theory and Applications, 2013, 11(1): 86–91. DOI:10.1007/s11768-013-1031-4 |
 2015, Vol. 38
2015, Vol. 38

