风电增速齿轮箱是风力发电机组的关键部件,它受无规律变向载荷的风力作用,在强阵风冲击的变载荷条件下工作,这使各路行星轮传递的功率分配更加不均匀,而均载是行星齿轮传动系统中需要解决的首要问题。人字齿轮因具有重合度高、轴向载荷小、承载能力高、工作平稳性好等优点,在船舶等重型机械传动系统中得到广泛应用,但风电增速齿轮箱常采用直齿行星传动,人字行星传动还鲜有报道。
国内、外许多学者对行星传动行星轮均载分析做了较深入的研究。朱增宝等[1-10]对行星传动的动态和静态均载特性进行了理论和实验研究,考虑不同误差种类对系统均载特性的影响。Sondkar Prashant等[11-14]将人字齿轮当成2个斜齿轮来处理,分析了其动力学特性,考虑了左右端斜齿轮交错角的影响。对于均载特性的研究,主要集中在直齿、单斜齿行星传动等方面;而对人字齿轮的研究,主要是把人字齿轮当做直齿轮来处理,也有将其处理成2个斜齿轮来计算,但未对均载特性分析。
笔者把人字齿轮当作左右2斜齿轮耦合而成,由于在斜齿轮传动过程中,轮齿的啮合会产生轴向的动态啮合分力,因此系统具有扭转振动和横向振动外,还会引起轴向振动,从而形成了人字齿轮系统的啮合型弯-扭-轴耦合振动模型。通过分析左右端交错角和耦合扭转刚度对均载特性的影响,从而为进一步对风电增速齿轮的传动设计提供依据。
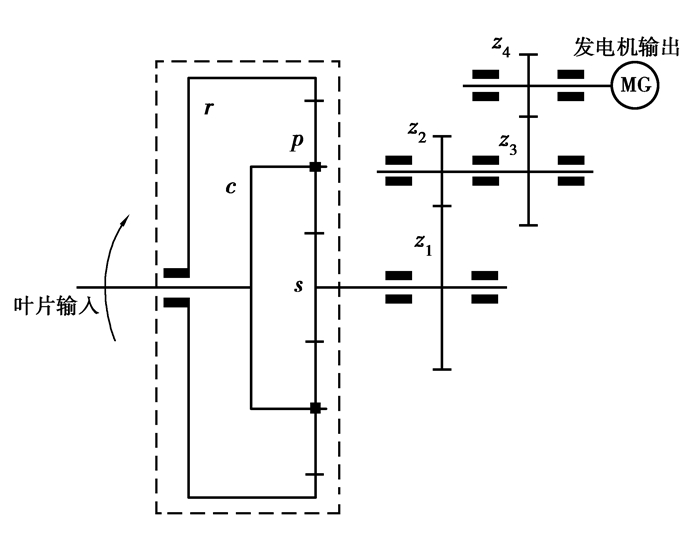
1 齿轮传动系统的动力学模型典型的风电增速齿轮箱的传动系统如图 1所示,输入扭矩通过行星架C传递给太阳轮S。基于集中质量参数法建立人字行星传动系统的动力学模型,模型中还考虑各个齿轮副的时变啮合刚度、啮合阻尼和啮合误差的影响。
|
图 1 风电增速齿轮箱的传动系统 Figure 1 Transmission system of wind turbine gearbox |
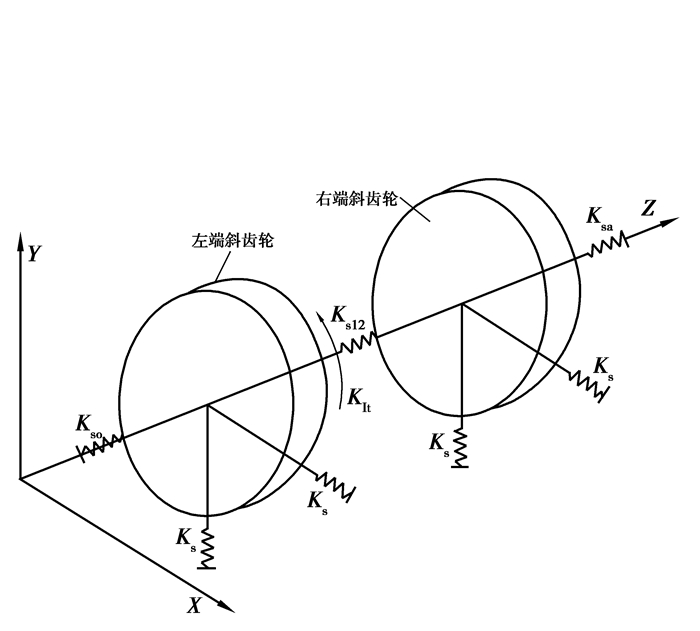
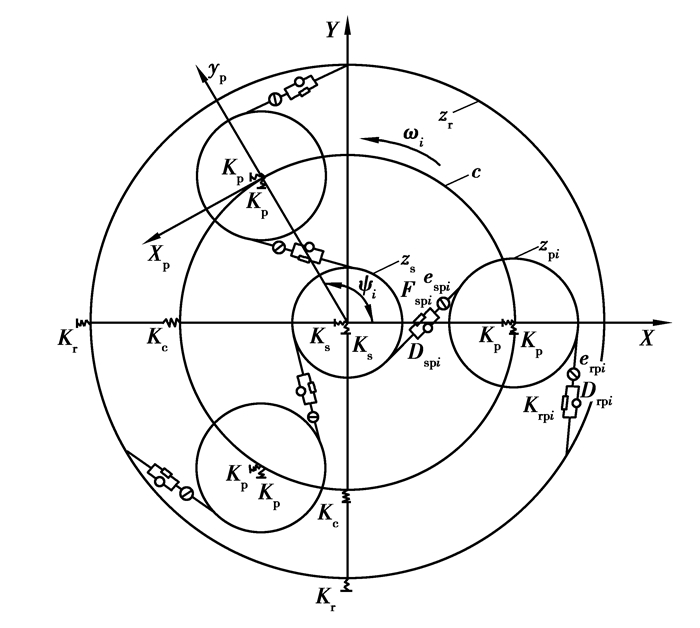
图 2是太阳轮左右端斜齿轮耦合关系,行星轮与内齿圈的耦合关系相似于太阳轮,图 3是传动系统以行星架转速wc为动坐标的动力学模型,其中Kspi、Cspi和espi分别为太阳轮与行星轮的啮合刚度、啮合阻尼和啮合误差,Krpi、Crpi和erpi分别为内齿圈与行星轮的啮合刚度、啮合阻尼和啮合误差。在图中,Ks12、Kp12和Kr12分别为太阳轮、行星轮和内齿圈左右2端斜齿轮之间的轴向刚度,Kct和Krt分别为行星架和内齿圈的切线支撑刚度,Ks、Kp和Kr分别为太阳轮、行星轮和内齿圈的径向支撑刚度,Ksa、Kpa和Kra分别为太阳轮、行星轮和内齿圈的轴向支撑刚度,K1t、K2t和K3t分别为太阳轮、行星轮和内齿圈之间的耦合扭转刚度。
|
图 2 太阳轮左右端斜齿轮耦合关系 Figure 2 The coupling relationship between the left and the right ends of the lical gear in sun gear |
|
图 3 传动系统动力学模型 Figure 3 Dynamic model of the transmission system |
此时,该人字行星传动系统共有17+8N个自由度,N为行星轮的个数,系统广义坐标X为
| X=[xs1,ys1,zs1,θzs1,xs2,ys2,zs2,θzs2,xpi1ypi1,zpi1,θzpi1,xpi2,ypi2,zpi2,θzpi2,xr1yr1,zr1,θzr1,xr2,yr2,zr2,θzr2,θzc], | (1) |
在广义坐标中,xs、ys和zs分别表示行星传动太阳轮的横向微位移、纵向微位移和轴向微位移,θzs表示太阳轮沿轴向的转动角度;xpi、ypi和zpi分别表示行星传动行星轮i的横向微位移、纵向微位移和轴向微位移,θzpi表示行星轮i沿轴向的转动角度;xr、yr和zr分别表示行星传动内齿圈的横向微位移、纵向微位移和轴向微位移,θzr表示内齿圈沿轴向的转动角度;θzc表示行星架沿轴向的转动角度;下标1和2分别代表人字齿轮的左端和右端。
2 系统的动力学方程设δspi1、δspi2和δrpi1、δrpi2为传动系统第i个行星轮与太阳轮和内齿圈沿啮合线的等效左右端的微位移,则
| {δspi1=[xs1sinψspi−xpi1sinαsn+ys1cosψspi−ypi1cosαsn+rsθzs1+rpiθzpi1]cosβb+(−zs1+zpi1)sinβb+e(1)spi(t)δspi2=[xs2sinψspi−xpi2sinαsn+ys2cosψspi−ypi2cosαsn+rsθzs2+rpiθzpi2]cosβb+(zs2+zpi2)sinβb+e(2)spi(t)δrpi1=−xr1sinψrpi+xpi1sinαrn+yr1cosψrpi−ypi1cosαrn+rrθzr1−rpiθzpi1cosβb+(zr1+zpi1)sinβb+e(1)rpi(t)δrpi2=−xr2sinψrpi+xpi2sinαrn+yr2cosψrpi−ypi2cosαrn+rrθzr2−rpiθzpi2cosβb+(−zr2+zpi2)sinβb+e(2)rpi(t), | (2) |
根据式(2)中的所求得微位移,乘以各自的啮合刚度可以得到每对齿轮副之间的啮合力,同理可以得到齿轮副的啮合阻尼力。设Fspi1、Dspi1和Frpi1、Drpi1分别为人字行星传动系统左端行星轮与太阳轮和内齿圈的啮合力和啮合阻尼,Fspi2、Dspi2和Frpi2、Drpi2分别为人字行星传动系统又端行星轮与太阳轮和内齿圈的啮合力和啮合阻尼
| {Fspi1=Kspi×δspi1,Fspi2=Kspi×δspi2,{Dspi1=Cspi×˙δspi1,Dspi2=Cspi×˙δspi2,{Frpi1=Krpi×δrpi1,Frpi2=Krpi×δrpi2,{Drpi1=Crpi×˙δrpi1,Drpi2=Crpi×˙δrpi2, | (3) |
根据Lagrange方程,将作用在各个构件上的惯性力、阻尼力与外部激励力组成平衡力系,可以推导出行星系统各个自由度的振动微分方程。
太阳轮的平衡方程
| {msx¨xs1+N∑i=1(Fspi1+Dspi1)sinψspicosβb+Ksxs1=0ms¨ys1+N∑i=1(Fspi1+Dspi1)cosψspicosβb+Ksys1=0ms¨zs1+N∑i=1(Fspi1+Dspi1)sinβb+Ks12(zs1−zs2)+Ksazs1=0Js¨θzs1+N∑i=1(Fspi1+Dspi1)rscosβb+K1t(us1−us2)=−Tout2, | (4) |
| {ms¨xs2+N∑i=1(Fspi2+Dspi2)sinψspicosβb+Ksxs2=0ms¨ys2+N∑i=1(Fspi2+Dspi2)cosψspicosβb+Ksyy2=0ms¨zs2+N∑i=1(Fspi2+Dspi2)sinβb+Ks12(zs2−zs1)+Ksazs2=0Js¨θzs2+N∑i=1(Fspi2+Dspi2)rscosβb+K1t(us2−us1)=−Tout2, | (5) |
行星轮的平衡方程
| {mp¨xpi1−(Fspi1+Dspi1)sinαsncosβb+(Frpi1+Drpi1)sinαrncosβb+Kpxpi1=0mp¨ypi1−(Fspi1+Dspi1)cosαsncosβb−(Frpi1+Drpi1)cosαrncosβb+Kp(ypi1−rcuc)=0mp¨zpi1+(Fspi1+Dspi1)sinβb+(Frpi1+Drpi1)sinβb+Kp12(zpi1−zpi2)+Kpazpi1=0Jp¨θzpi1+(Fspi1+Dspi1)rpicosβb−(Frpi1+Drpi1)rpicosβb+K2t(upi1−upi2)=0, | (6) |
| {mp¨xpi2−(Fspi2+Dspi2)sinαsncosβb+(Frpi2+Drpi2)sinαrncosβb+Kpxpi2=0mp¨ypi2−(Fspi2+Dspi2)cosαsncosβb−(Frpi2+Drpi2)cosαrncosβb+Kp(ypi2−rcuc)=0mp¨zpi2+(Fspi2+Dspi2)cosβb+(Frpi2+Drpi2)cosβb+Kp12(zpi2−zpi2)+Kpazpi2=0Jp¨θzpi2+(Fspi2+Dspi2)rpicosβb−(Frpi2+Drpi2)rpicosβb+K2t(upi2−upi1)=0, | (7) |
内齿圈的平衡方程
| {mr¨xr1−N∑i=1(Frpi1+Drpi1)sinψrpicosβb+Krxr1=0mr¨yr1+N∑i=1(Frpi1+Drpi1)cosψrpicosβb+Kryr1=0mr¨zr1+N∑i=1(Frpi1+Drpi1)sinβb+Kr12(zr1−zr2)+Krazr1=0Jr¨θzr1+N∑i=1(Frpi1+Drpi1)rrcosβb+Krtθzr1+K3t(ur1−ur2)=0, | (8) |
| {mr¨xr2−N∑i=1(Frpi2+Drpi2)sinψrpicosβb+Krxr2=0mr¨yr2+N∑i=1(Frpi2+Drpi2)cosψrpicosβb+Kryr2=0mr¨zr2+N∑i=1(Frpi2+Drpi2)sinβb+Kr12(zr2−zr1)+Krazr2=0Jr¨θzr2+N∑i=1(Frpi2+Drpi2)rrcosβb+Krtθzr2+K3t(ur2−ur1)=0, | (9) |
行星架的平衡方程
| Jc¨θzc+N∑i=1Kprc(θzcrc−ypi1+θzcrc−ypi2)+Kctθzc=−Tin, | (10) |
式中:m为各个构件的等效质量和平移质量;J为各构件的转动惯量。Tin为传动系统行星架的输入扭矩,Tout为传动系统太阳轮的输出扭矩。
将方程(4)-(10)整理成如下的矩阵形式
| [M]{˙X}+[C]{˙X}+[K(t)]{X}=[F(t)], | (11) |
式中:M,X-广义质量矩阵,广义坐标位移列阵;C,F-阻尼矩阵,外载荷列阵;K(t)-时变刚度矩阵。
3 综合啮合误差激励齿轮的制造误差和安装误差是齿轮传动系统产生振动的主要因素。各齿轮的偏心误差对齿轮啮合的激励是表现在啮合线方向上的位移激励,研究时把以上误差转化到齿轮副啮合线上。
将误差的变化规律表示成Fourier级数的形式,总共有4N个周期激励,其基频均为齿轮啮合频率
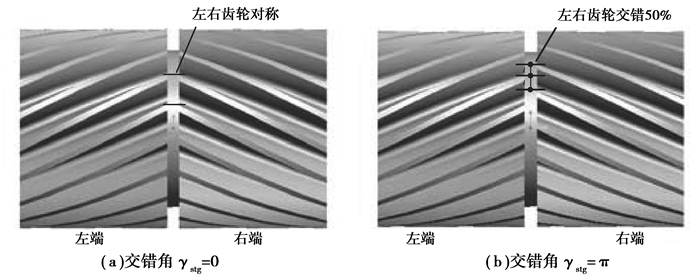
| {e(1)spi(t)=L∑l=1ˆesplcos(lwmt+σspl−lzsψi)e(2)spi(t)=L∑l=1ˆesplcos(lwmt+σspl−lzsψi+lγstg)e(1)rpi(t)=L∑l=1ˆerplcos(lwmt+σrpl+lγrs+lzrψi)e(2)rpi(t)=L∑l=1ˆerplcos(lwmt+σrpl+lγrs+lzrψi+lγstg), | (12) |
式中:
|
图 4 左右端斜齿轮交错角示意图 Figure 4 Illustration of the right-to-left stagger conditions in adoble helical gear pair |
对于传动系统多自由度微分方程组(11),求其解析解是比较困难的,一般均采用数值解法来求解。采用四阶Runge-Kutta法求解方程组。将式(11)中得到的位移响应代到式(3)中,得到弹性啮合力Fspi1、Frpi1、Frpi2和Frpi2。令bspi1、brpi1和brpi2、brpi2分别为人字行星系统左右端的在一个啮频周期内外啮合与内啮合的均载系数
| {bspij=N(Fspij)maxN∑j=1(Fspij)maxbrpij=N(Frpij)maxN∑j=1(Frpij)maxbspik=N(Fspik)maxN∑k=1(Fspik)maxbrpik=N(Frpik)maxN∑k=1(Frpik)max, | (13) |
式中:j=1, 2, …, n1;k=1, 2, …, n2,j和k分别为啮频周期数。
定义系统在一个啮频周期中的均载系数为
| {Bspi1=|bspij−1|max+1Brpi1=|brpij−1|max+1Bspi2=|bspik−1|max+1Brpi2=|brpij−1|max+1, | (14) |
定义Bsp1和Brp1分别为系统左端啮频周期内外啮合的均载系数;令Bsp2和Brp2分别为系统右端啮频周期内外啮合的均载系数。则左右端系统啮频周期内外啮合均载系数为
| {Bsp1=max(Bspi1)Brp1=max(Brpi1)Bsp2=max(Bspi2)Brp2=max(Brpi2)。 | (15) |
取自某风电增速齿轮箱的已有算例,其主要技术参数为:取行星架输入转速为17 r/min,输入扭矩Tin=9.33×105 Nm;行星轮个数3;太阳轮与行星轮的等效啮合刚度为3.06×109 N/m,行星轮与内齿圈的等效啮合刚度3.70×109 N/m;太阳轮、行星轮与内齿圈的径向支承刚度为1×1010 N/m,轴向支承刚度为8.54×109 N/m。
齿轮传动主要参数如下:太阳轮zs=19,行星轮zp=33,内齿轮zr=86;模数mn=8.4667;压力角α=20°;螺旋角β=24.5°。在KISSsoft中可以计算得到齿轮传递误差的初始幅值和相位。由于这里高于3次谐波的幅值很小,所以只取前三阶谐波,其值如表 1所示。
| 表 1 传递误差的初始幅值和相位 Table 1 Harmonic amplitudes and phase angles of the transmission error |
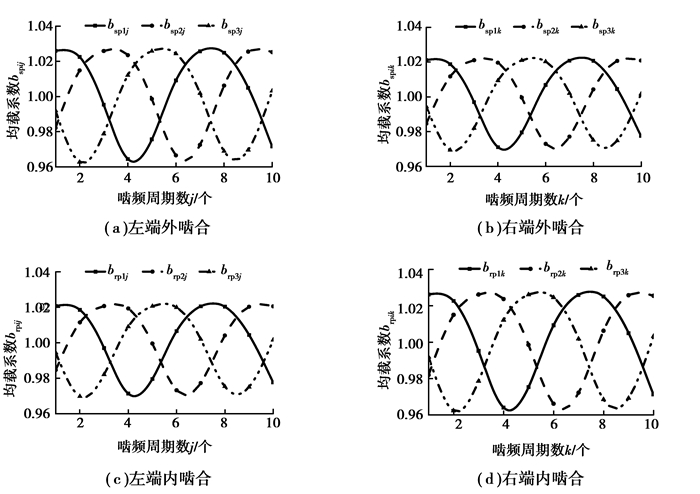
为研究齿轮交错角对各行星轮均载特性影响,采用式(13)计算每一啮频周期系统各行星轮内外啮合均载系数,得到γstg=0时左右端各行星轮内外啮合均载系数随啮频周期数变化曲线如图 5所示。由于人字齿左右端存在耦合关系,所以左右端均载系数变化不相同。
|
图 5 左右端各行星轮内外啮合均载系数曲线 Figure 5 External and internal load sharing of the left and the right ends of each planet meshing |
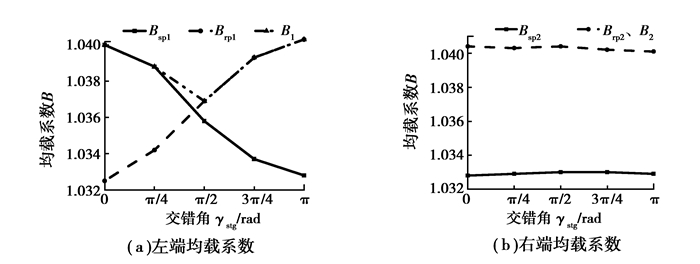
当左右端斜齿轮之间的交错角γstg=0、π/4、π/2、3π/4和π时,分别采用式(14)、(15)计算左右端系统周期内外均载系数。获得左右端内外啮合一个啮频周期内的均载系数分别随交错角的变化曲线如图 6所示。
|
图 6 左右端均载系数分别随交错角的变化曲线 Figure 6 Effect of stagger angel on external and internal load sharing |
可以看出,交错角对左端系统啮频周期内的均载性能影响较大,而对右端均载性能影响较小。在交错角为0~π/2时,左端外啮合均载系数随着交错角的增大而减小,内啮合均载系数随着交错角的增大而增大。左端系统综合均载系数是随着交错角的增大先减小后增大,在γstg=π/2时,其达到最小值为1.0369;而右端均载系数随着交错角的增大先增大后减小,在γstg=π/2时,其均载系数达到最大值1.0404。由于右端均载系数基本未发生变化,而左端均载系数在交错角为π/2时均载性能最好,可以得出人字齿传动系统综合均载效果在交错角为π/2时最好。
5.2 耦合扭转刚度对动态均载特性的影响分析上述的分析仅考虑了交错角对系统均载特性的影响。假设交错角为0,分析此时左右端斜齿轮的耦合扭转刚度对动态均载特性的影响。
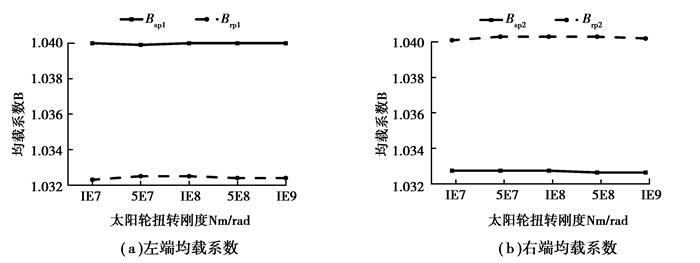
为研究耦合扭转刚度对系统均载性能的影响,行星轮和内齿圈扭转刚度不变,均取108 Nm/rad,太阳轮左右端耦合扭转刚度分别取107、5×107、108、5×108和109 Nm/rad,获得系统周期内均载系数变化曲线如图 7所示。
|
图 7 太阳轮耦合扭转刚度与均载系数的变化曲线 Figure 7 Effect of coupling torsional stiffness in sun on external and internal load sharing |
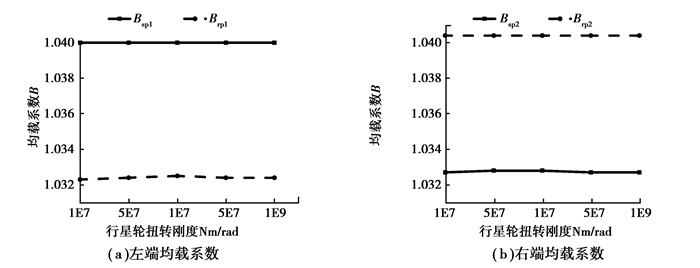
当行星轮左右端耦合扭转刚度取107、5×107、108、5×108和109 Nm/rad,太阳轮和内齿圈耦合扭转刚度均取108 Nm/rad,获得系统周期内均载系数变化曲线如图 8所示。
|
图 8 行星轮耦合扭转刚度与均载系数的变化曲线 Figure 8 Effect of coupling torsional stiffness in plant on external and internal load sharing |
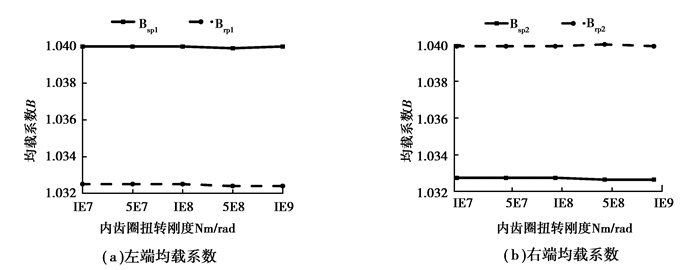
当内齿圈左右端耦合扭转刚度取107、5×107、108、5×108和109Nm/rad,太阳轮和行星轮耦合扭转刚度均取108Nm/rad,获得系统周期内均载系数变化曲线如图 9所示。
|
图 9 内齿圈耦合扭转刚度与均载系数的变化曲线 Figure 9 Effect of coupling torsional stiffness in internal gear on external and internal load sharing |
通过分析可以得出:太阳轮、行星轮和内齿圈左右端的耦合扭转刚度对系统均载系数影响不大。
6 总结1) 基于Lagrange方程采用集中参数法建立了人字齿行星传动系统的动力学方程,考虑了交错角和耦合扭转刚度对均载特性的影响。
2) 人字齿左右端斜齿轮之间的交错角对左端均载性能有较大的影响,而右端均载性能对其不敏感。在交错角为π/2时,左端的均载性能达到最优,而右端均载性能最差;综合分析得出此时左右端的综合均载性能最好。
3) 在交错角为0的情况下,太阳轮、行星轮和内齿圈左右端耦合扭转刚度对系统的均载性能影响不大。
| [1] |
朱增宝, 朱如鹏, 李应生, 等.
安装误差对封闭差动人字齿轮传动系统动态均载特性的影响[J]. 机械工程学报, 2012, 48(3): 16–24.
ZHU Zengbao, ZHU Rupeng, LI Yingsheng, et al. Impact of installation error on dynamics load sharing characteristic for encased differential herringbone train[J]. Journal of Mechanical Engineering, 2012, 48(3): 16–24. DOI:10.3901/JME.2012.03.016 (in Chinese) |
| [2] |
周志刚, 秦大同, 杨军, 等.
变载荷下风力发电机行星齿轮传动系统齿轮-轴承耦合动力学特性[J]. 重庆大学学报:自然版, 2012, 35(12): 7–14.
ZHOU Zhigang, QIN Datong, YANG Jun, et al. Gear-bearing coupling dynamics characteristics of wind turbine planetary gear transmission system under variable load[J]. Journal of Chongqing University, 2012, 35(12): 7–14. (in Chinese) |
| [3] | Kahraman A. Load sharing characteristics of planetary transmissions[J]. Mechanisms and Machine Theory, 1994, 29(8): 1151–1165. DOI:10.1016/0094-114X(94)90006-X |
| [4] | Krantz T L. A method to analyze and optimize the load sharing of split path transmissions[R]. 107201. San Diego: NASA Technical Memorandum, 1996: 1-10. |
| [5] | Ajmi M, Velex P. A model for simulating the quasi static and dynamic behavior of solid wide-faced spur and helical gears[J]. Mechanism and Machine Theory, 2005(40): 173–190. |
| [6] | Ajmi M, Velex P. A model for simulating the quasi static and dynamic behavior of double helical gears[J]. The JSME International Conference on Motion and Power Transmission, MPT-2001, 2001: 132–137. |
| [7] | Platt R, Leopold R. A Study on Helical Gear Planetary Phasing Effects on Transmission Noise[J]. VDI Berichte, 1996: 793–807. |
| [8] |
王成, 方宗德, 贾海涛.
人字齿轮均载特性的理论分析与试验研究[J]. 兵工学报, 2011, 32(1): 74–77.
WANG Cheng, FANG Zongde, JIA Haitao. Theoretical calculation and experimental study of load sharing for double helical gears[J]. ACTA ARMAMENTARII, 2011, 32(1): 74–77. (in Chinese) |
| [9] |
吴文光.人字齿轮传动系统的建模及其动力学特性的有限元分析研究[D].南京:南京航空航天大学, 2010. WU Wenguang. Parametric modeling of herringbone gear drive system and finite element analysis of its dynamic characteristics[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010. http://www.oalib.com/references/16426040 |
| [10] | Kubur M, Kagraman A, Zini D M, et al. Dynamic analysis of a multi-Shaft helical gear transmission by finite elements: model and experiment[J]. ASME Journal of Vibration and Acoustics, 2004, 126(3): 398–406. DOI:10.1115/1.1760561 |
| [11] | Sondkar P, Tech M. A dynamic modeling of double-helical planetary gear set[J]. Mechanism and Machine Theory, 2013, 70: 157–174. DOI:10.1016/j.mechmachtheory.2013.07.005 |
| [12] | Parker R, Lin J. Mesh phasing relationships in planetary and epicyclic gears[J]. ASME Journal of Mechanical Design, 2004, 126(2): 365–370. DOI:10.1115/1.1667892 |
| [13] |
王成, 高常青, 崔焕勇.
基于啮合特性的人字齿轮动力学建模与分析[J]. 中南大学学报:自然科学版, 2012, 43(8): 3019–3024.
WANG Cheng, GAO Changqing, CUI Huanyong. Dynamic modeling and analysis of double helical gears based on meshing characters[J]. Journal of Central South University:Science and Technology, 2012, 43(8): 3019–3024. (in Chinese) |
| [14] |
王峰, 方宗德, 李声晋.
滚动轴承支撑人字齿轮传动系统动力传递过程分析研究[J]. 机械工程学报, 2014, 50(3): 25–32.
WANG Feng, FANG Zongde, LI Shengjin. Research and analysis on power transmission processing of herringbone gear trains system with rolling bearing support[J]. Journal of Mechanical Engineering, 2014, 50(3): 25–32. DOI:10.3901/JME.2014.03.025 (in Chinese) |
| [15] | 李润方, 王建军. 齿轮系统动力学[M]. 北京: 科学出版社, 1996. |
 2015, Vol. 38
2015, Vol. 38



