齿轮箱是风机的关键传动部件,齿轮系统在其内部激励和外部激励作用下会产生振动,随着机组容量的增加,齿轮箱体积增大以及弹性增加,振动问题更加突出,这些问题促使人们在丰富齿轮系统分析模型、理论创新等方面进行深入的研究[1-2],在产品设计时更强调齿轮箱的动力学性能[3-6]。
风电齿轮箱系统是由齿轮箱箱体、齿轮副、轴以及轴承等零部件组成的复杂机械弹性系统[7-8],其动态特性计算有一定的复杂性和数据处理量,随着有限元理论的日趋成熟以及相关计算软件的商业化,出现了一些对风电齿轮箱进行振动噪声分析优化的研究[9-12]。其中,文献[10-11]对常用一级NGW行星和两级平行齿轮结构的小兆瓦齿轮箱进行振动分析并优化,但计算还需进一步试验的佐证。大兆瓦方面,魏静等[12]对行星轮只有自转运动的NW结构3 MW齿轮箱进行分析,建立其系统耦合非线性动力学模型,研究了在外部变载激励及内部激励下的振动响应,且与试验结果很好地吻合。
随着风力机组容量的增大,主流采用两级NGW行星和一级平行齿轮结构的3 MW及更大的主齿轮箱获得越来越多的应用,其振动特性较NW行星结构齿轮箱更加复杂,以市场上逐渐广泛使用的某款3 MW风电主齿轮箱为研究对象,建立能有效模拟实际使用状态的试验台动力学模型,研究其在极限工况下的振动特性,并将计算结果与测试数据进行对比,验证模型建立与各参数选取的准确性,为后续产品优化提供参考,通过这些分析对风电齿轮箱设计中优化其动态特性,减少振动噪声,缩短产品开发周期有一定的参考。
1 动力学分析 1.1 动力学模型该齿轮箱为两级NGW行星和一级平行齿轮结构,在试验台中,扭力臂使用与实际风机相同的弹性支撑,输出轴与电机转子间的连接使用与实际风机相同的柔性联轴器,以模拟实际工作状态。
在壳体和转架轴承安装孔及连接面上建立凝聚节点,通过提取其凝缩刚度矩阵、质量矩阵、固有频率及重力数据应用于动力学模型中以考虑其柔性和模态信息。
所有轴系采用有限单元Timshenko梁处理,轴承使用基于赫兹理论计算的非线性刚度。建立的模型如图 1和图 2所示。

|
图 1 齿轮箱MASTA模型 Figure 1 MASTA model of gearbox |
|
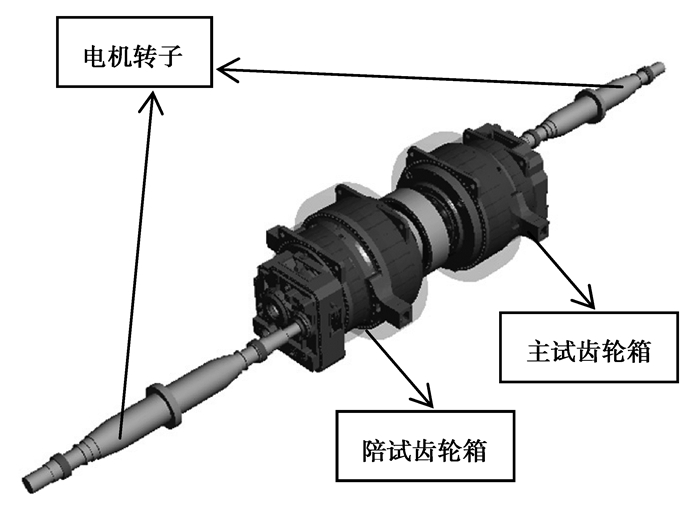
图 2 齿轮箱试验台架模型 Figure 2 Test rig model of gearbox |
主要分析与实际风机使用状态相同的主试齿轮箱。根据齿轮参数,齿轮箱在极限工况下的各级齿轮副啮合频率如表 1所示。
| 表 1 各级齿轮副啮合频率 Table 1 Mesh frequency of each stage |
工程经验上,固有频率计算时,其数值要覆盖整机最高啮合频率的3倍频[13]。同时在某阶激励频率±10%范围内的固有频率,若其较大动能分布在激励源上,则可能会发生振动,而重叠则可能会发生共振,为满足要求,笔者取系统前500阶固有频率进行计算。
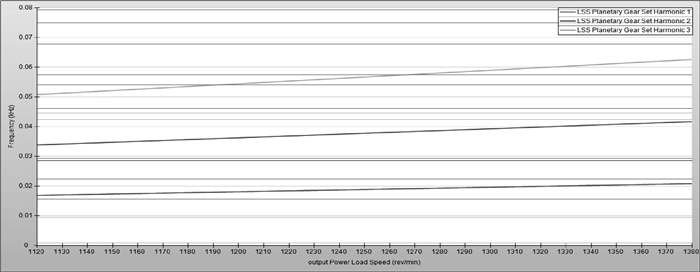
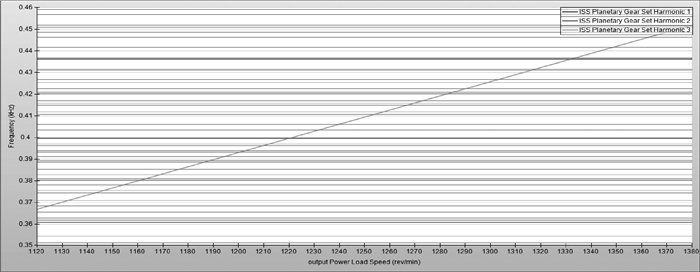
做齿轮副啮合激励和固有频率的坎贝尔图,横轴为极限转速±10%,纵轴为固有频率,相交点为需要进一步分析的固有频率,如图 3~9所示。
|
图 3 LSS前三阶坎贝尔图 Figure 3 Campbell chart of LSS first three order |
|
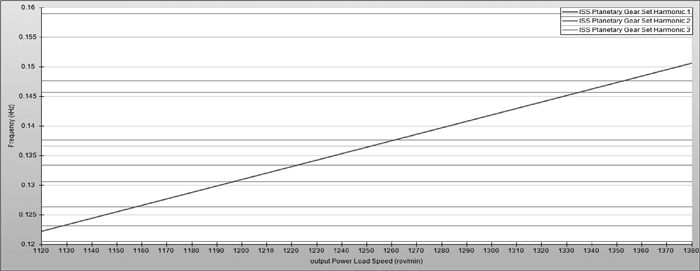
图 4 IMS第一阶坎贝尔图 Figure 4 Campbell chart of IMS first order |
|
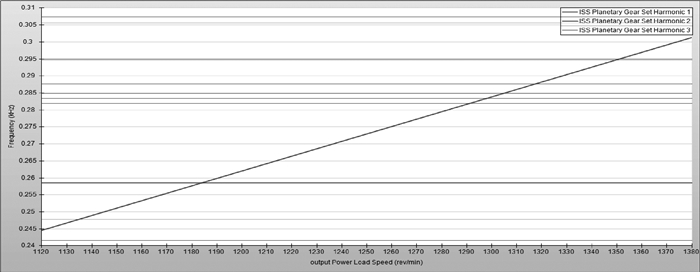
图 5 IMS第二阶坎贝尔图 Figure 5 Campbell chart of IMS second order |
|
图 6 IMS第三阶坎贝尔图 Figure 6 Campbell chart of IMS third order |

|
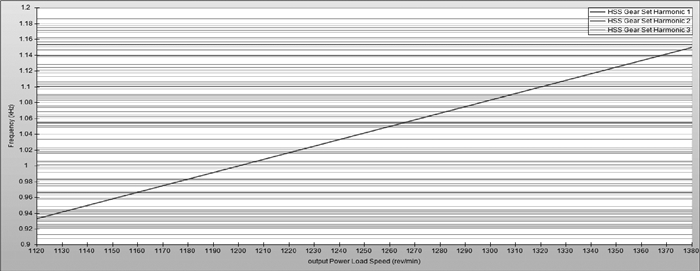
图 7 HSS第一阶坎贝尔图 Figure 7 Campbell chart of HSS first order |
|
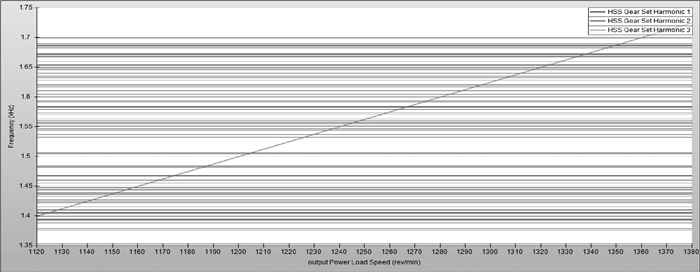
图 8 HSS第二阶坎贝尔图 Figure 8 Campbell chart of HSS second order |
|
图 9 HSS第三阶坎贝尔图 Figure 9 Campbell chart of HSS third order |
坎贝尔图得到相交的固有频率阶数如表 2所示。
| 表 2 相交固有频率阶数 Table 2 Intersected natural frequency orders |
表 2中,对主试齿轮箱中每阶有零部件动能占比超过10%的频率进行分析,限于篇幅,笔者着重分析每级齿轮啮合频率第一阶处的振动情况,根据模态阵型和动能分布,将满足条件的固有频率及其动能分布情况整理如表 3所示。
| 表 3 动能分布 Table 3 Kinetic energy distribution |
由动能分布可知,在LSS一阶啮合激励频率±10%范围内无固有频率,在IMS一阶激励频率处IMS组件无较大动能分布,10%范围内动能主要分布在壳体上,IMS行星轮和HSS高速轴有一定动能分布。HSS一阶激励频率处无较大动能分布,10%范围内动能主要分布在壳体上,且有四阶频率壳体动能占比超过50%,另除了高速级上,其余部件上均有一定动能分布,但动能占比较小。
综上分析,此齿轮箱不会产生明显共振,但会有一定振动,高速级齿轮啮合频率较低速级和中间级更易发生一定振动,且壳体上振动应最大。
1.3 齿轮箱响应分析齿轮系统的主要激振源是轮齿啮合的动态激励[14],动态激励包括刚度激励、误差激励和啮合冲击激励。刚度激励的产生是由于啮合过程中单、双齿对啮合交替出现导致轮齿综合啮合刚度和轮齿载荷周期性变化,进而引起对齿轮系统的动态激励。其激励力可表示为
| $ F = D \times \delta , $ | (1) |
| $ D = {\left( {{C_{\rm{P}}} + {C_{\rm{W}}}} \right)^{ - 1}}, $ | (2) |
式中:F为啮合力;D为动态啮合刚度;δ为静态传递误差;CP为小轮柔度;CW为大轮柔度。
在实际试验台中,由于两低速级联轴器的对中性以及高速轴在重载后的弯曲扭转变形影响,会产生一定的误差激励和冲击激励,即实际激励力比计算的刚度激励更大,故在计算中增大LSS和HSS的齿轮传递误差来实现激励力的增大。
由分析得到,最大响应发生在壳体上,故选取齿轮箱体上两测点MP1,MP2,计算其在X(水平)、Y(轴向)、Z(垂直)方向上的响应。
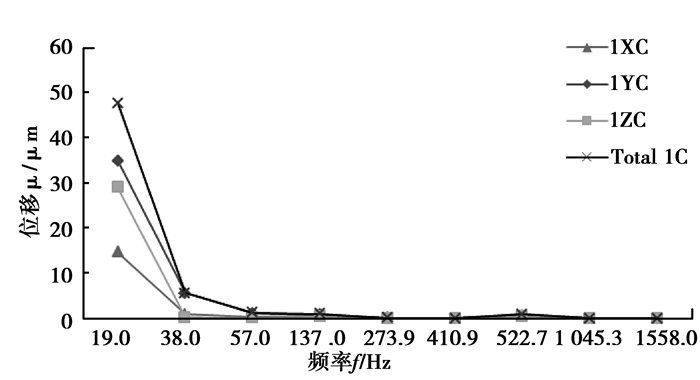
以横轴代表齿轮副LSS、IMS、HSS级的1、2、3阶激励频率,计算结果分别如图 10~15所示。
|
图 10 测点1位移响应 Figure 10 Displacement response of measured point 1 |
|
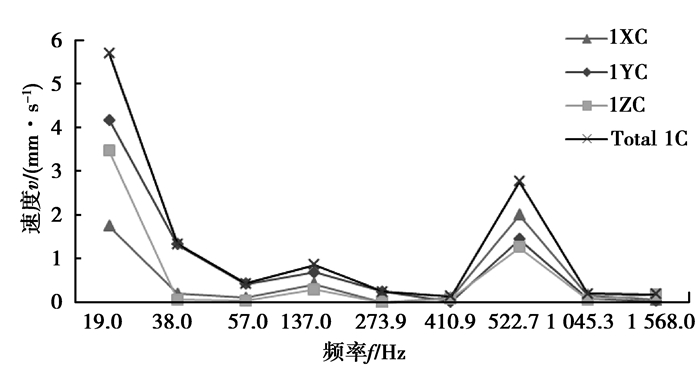
图 11 测点1速度响应 Figure 11 Velocity response of measured point 1 |
|
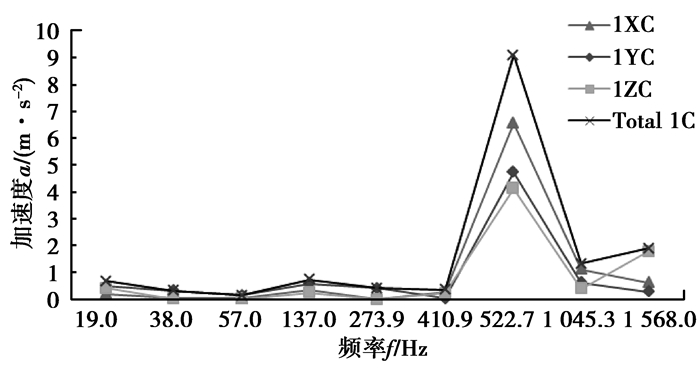
图 12 测点1加速度响应 Figure 12 Acceleration response of measured point 1 |
|
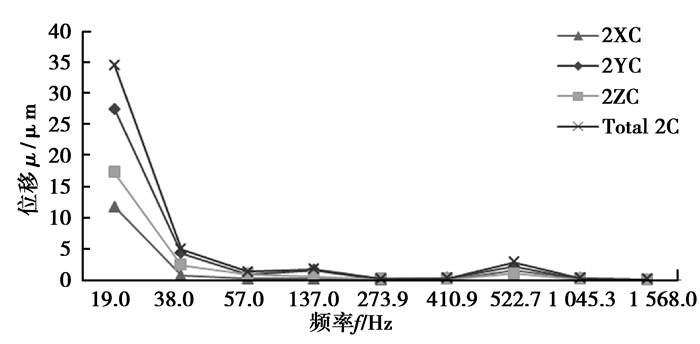
图 13 测点2位移响应 Figure 13 Displacement response of measured point 2 |
|
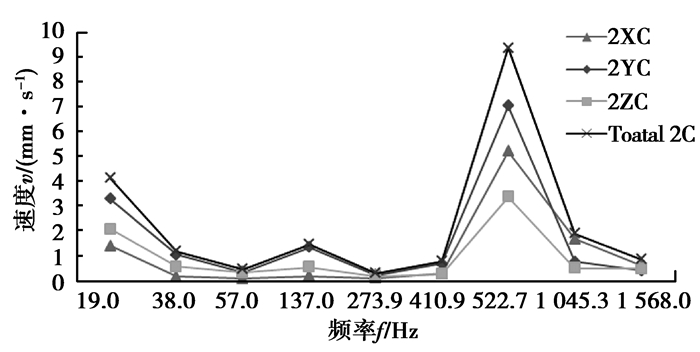
图 14 测点2速度响应 Figure 14 Velocity response of measured point 2 |
|
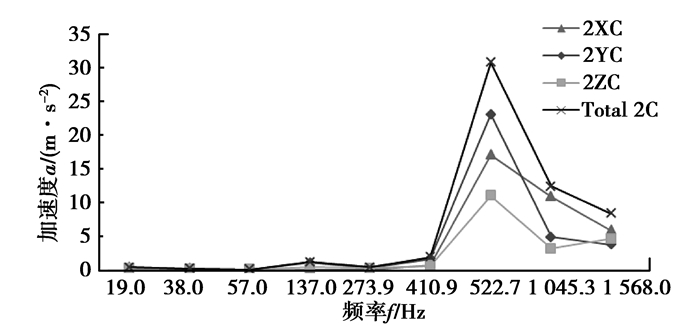
图 15 测点2加速度响应 Figure 15 Acceleration response of measured point 2 |
由表可以看出,测点1的振动速度最大值发生在LSS一阶啮合频率上,测点2的振动速度最大值发生在HSS一阶啮合频率上。测点1和测点2振动加速度最大值均发生在HSS级一阶啮合频率上,且距离HSS级更近的测点2振动加速度更大,每级齿轮的第一阶啮合频率激励下,齿轮箱有更大的振动响应。
由上分析可知,HSS一阶啮合激励引起的壳体振动最强烈,高速级零部件承受更大的额外动载荷,在设计中,要着重进行高速级的结构及齿轮激励优化。
2 试验对比使用高功率电机对齿轮箱进行加载。本次试验测试振动速度,共进行了5次测量,笔者使用此5组数据的平均值与计算值进行比较。
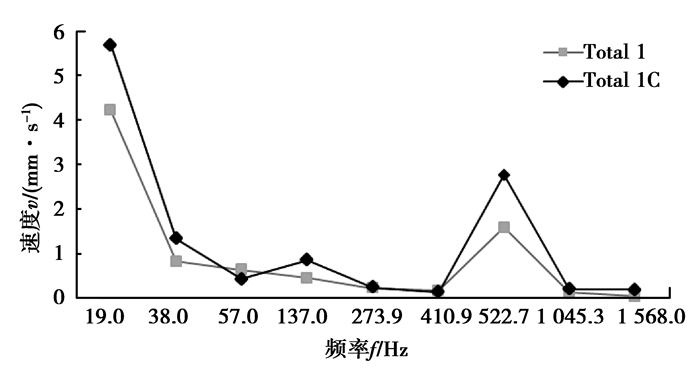
在测量点MP1、MP2上其振动速度和计算进行比对如图 16、图 17所示。
|
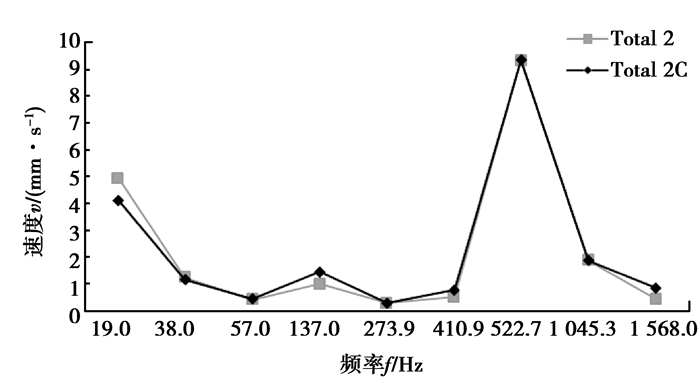
图 16 测点1比对 Figure 16 Comparison of measured point 1 |
|
图 17 测点2比对 Figure 17 Comparison of measured point 2 |
其中,Total 1为测量值,Total 1C为计算值,以此类推。
测点1、2在每阶激励下计算值和试验测量值对比如表 4所示。
| 表 4 振动速度对比 Table 4 Vibration velocity comparison |
由上可知,计算数据与测试数据趋势一致。除某些较小振动速度值处,如LSS 3st和HSS 3st,由于测量现场及精度原因,有一定偏差,在较大振动速度值处,计算和试验结果有较好的一致性。通过以上对比,验证了动力学模型的准确性。
3 结语建立某3 MW风电齿轮箱多柔体动力学模型,并基于坎贝尔图和动能分布对其进行振动分析。壳体在各级齿轮啮合频率附近有最大的动能占比,在每级齿轮的第一阶啮合频率激励下,齿轮箱有更大的振动响应,且齿轮箱在高速级第一阶啮合频率处振动最大;对齿轮箱进行振动测试,并将计算数据与其进行对比,两者具有一定的吻合度,为后续产品进行设计改进积累一定的计算基础;本文结果对风电齿轮箱设计阶段进行振动风险规避提供一定的计算参考。
| [1] | Hall J F, Mecklenborg C A, Chen D M, et al. Wind energy conversion with a variable-ratio gearbox:design and analysis[J]. Renewable Energy, 2011, 36(3): 1075–1080. DOI:10.1016/j.renene.2010.08.037 |
| [2] |
王建军, 李润方.
齿轮系统动力学的理论体系[J]. 中国机械工程, 1998, 9(12): 55–58.
WANG Jianjun, LI Runfang. The theoretical system of the gear vibration theory[J]. China Mechanical Engineering, 1998, 9(12): 55–58. (in Chinese) |
| [3] | Smith J D. Gear noise and vibration[M]. 2th. New York: Marcel Dekker, 2003. |
| [4] | Krouse J. Wind turbine gearbox vibration[J]. Power Engineering, 2009, 113(10): 16. |
| [5] |
张庆伟, 张博, 王建宏, 等.
风力发电机齿轮传动系统的动态优化设计[J]. 重庆大学学报, 2010, 33(3): 30–35.
ZHANG Qingwei, ZHANG Bo, WANG Jianhong, et al. Dynamic optimization design of gear transmission system for wind turbine[J]. Journal of Chongqing University, 2010, 33(3): 30–35. (in Chinese) |
| [6] |
朱才朝, 黄泽好, 唐倩, 等.
风力发电齿轮箱系统耦合非线性动态特性的研究[J]. 机械工程学报, 2005, 41(8): 203–207.
ZHU Caichao, HUANG Zehao, TANG Qian, et al. Analysis of nonlinear coupling dynamic characteristics ofgearbox system about wind-driven generator[J]. Chinese Journal of Mechanical Engineering, 2005, 41(8): 203–207. DOI:10.3901/JME.2005.08.203 (in Chinese) |
| [7] | Peeters J L M, Vandepitte D, Sas P. Analysis of internaldrive train dynamics in a wind turbine[J]. Wind Energy, 2006, 9(1/2): 141–161. |
| [8] |
庞辉, 方宗德, 欧卫林.
多平行齿轮耦合转子系统的振动特性分析[J]. 振动与冲击, 2007, 26(6): 21–25.
PANG Hui, FANG Zongde, OU Wei-lin. Analysis on lateral-torsional coupling vibration characteristics ofmulti-parallelgear-rotor system[J]. Journal of Vibration and Shock, 2007, 26(6): 21–25. (in Chinese) |
| [9] | Heege A, Betran J, Radoveic Y. Fatigue load computation ofwind turbine gearboxes by coupled finite element, multi-body system and aerodynamic analysis[J]. Wind Energy, 2007, 10(5): 395–413. DOI:10.1002/(ISSN)1099-1824 |
| [10] | 孟令宽.风电增速箱非线性振动噪声分析及动力优化[D].重庆:重庆大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10611-1012048133.htm |
| [11] | 彭秋林.兆瓦级风力发电机齿轮传动系统动力学分析及优化设计[D].重庆:重庆大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10611-1013043583.htm |
| [12] |
魏静, 孙清超, 孙伟, 等.
大型风电齿轮箱系统耦合动态特性研究[J]. 振动与冲击, 2012, 31(8): 16–23.
WEI Jing, SUN Qingchao, SUN Wei, et al. dynamical coupling characteristics of a large wind turbine gearbox transmiassion system[J]. Journal of Vibration and Shock, 2012, 31(8): 16–23. (in Chinese) |
| [13] | Brooktorkai. Guideline for the certification of Wind Turbine[M]. Germany: Germanischer Lloyd, Hamburg, 2010. |
| [14] | 李锦花, 史妍妍, 孔祥锋. 齿轮箱系统动态特性分析及优化[J]. 航空科学技术, 2012(6): 32–35. |
| [15] | LI Jinhua, SHI Yanyan, KONG Xiangfeng. Dynamic Characteristics Analysis and Optimization of Gearbox[J]. Aeronautical Science & Technology, 2012(6): 32–35. |
 2015, Vol. 38
2015, Vol. 38

