风电增速器是风力发电机组中的一个重要机械部件,由于机组工作环境较恶劣,使得由随机风载引起的附加动载荷对齿轮传动系统造成振动和冲击,是风机故障率最高的部件之一。同时齿轮箱在发生故障时维修工作进行起来也非常困难,因此对风电增速器的传动系统开展动态特性分析并进行合理化设计以提高风力发电机组整个的运行质量就显得尤为重要。在风电齿轮传动系统动力学特性的研究方面,国外很多学者很早就对单级行星轮系进行了建模分析[1-3],多采用牛顿运动定律建立行星轮系的动力学模型,构成了具有普遍分析意义的单级行星轮系分析模型。后来, Peeters等[4]从多体动力学的角度研究了螺旋角、支承刚度等对系统动力学特性的影响,并从此展开了多级行星齿轮传动的动力学特性研究,主要围绕分析模型、动态响应求解方法以及实验研究等方面展开[5-6]。在风电增速器齿轮箱的优化设计方面,很多学者已将可靠性优化设计方法运用到传动系统的优化设计中[7-8]。以齿轮传动系统的动力学性能作为优化目标或约束的动态优化设计相比于传统的静态准则设计在提高动态性能及缩短设计周期方面具有明显优势,因此目前齿轮传动系统的优化逐渐向着动态优化方向发展。近年来有不少学者进行齿轮动态优化设计的研究,通过建立系统的动力学分析模型并计算其在内外部激励下的动态响应,修改设计参数使其动态性能达到最优[9-11],但多数研究将动态特性优化与轻量化不能有机结合到一起。笔者在利用动态特性分析指导传动系统设计的同时,考虑到风电齿轮箱高空架设环境,在动态优化设计过程中将传动系统可靠性和体积轻量化融入其中,达到提高传动系统可靠性,减轻传动系统质量,优化其动态性能的目的,这些研究为风电增速器的设计提供基础,对提高齿轮箱的性能指标意义重大。
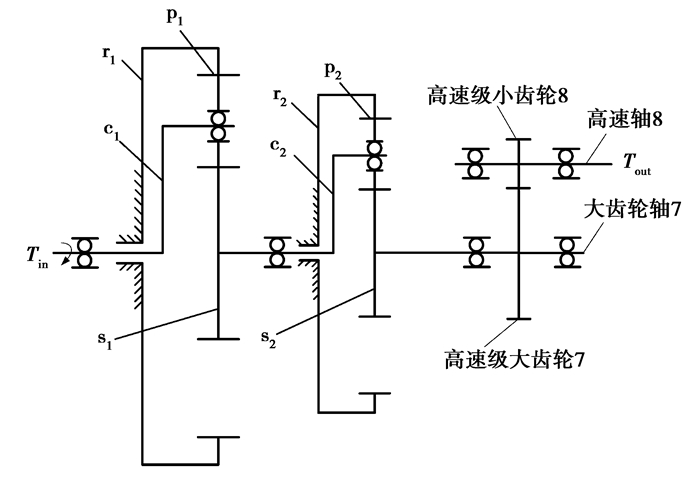
1 风电增速器齿轮传动系统动力学模型某大功率风电增速采用两级行星NGW型斜齿行星传动和一级标准斜齿轮传动形式,其齿轮传动系统结构图如图 1所示。
|
图 1 风电增速箱齿轮传动系统结构图 Figure 1 Structure of two-stage planetary transmission |
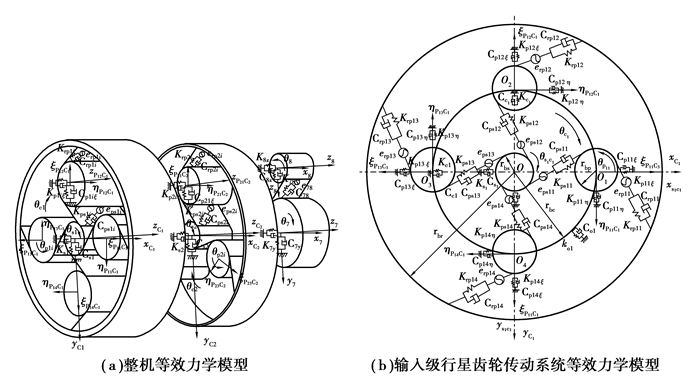
图 1中,第1级(输入级)行星轮系采用4个行星齿轮,第2级行星轮系采用3个行星齿轮。假定第1级与第2级行星轮为均匀分布,同一级行星齿轮物理参数均相同,同一级行星传动参与内、外啮合齿轮的螺旋角、齿宽及端面啮合角相同,其有效动力学模型如图 2所示。字母r、s、p、c、g分别表示内齿圈、太阳轮、行星轮、行星架及输出级齿轮;上标字母j代表行星级数,j=Ⅰ, Ⅱ;下标i代表同一行星级中第i个行星轮,当j=Ⅰ时,i=1,2, 3, 4;当j=Ⅱ时,i=1, 2, 3。则定义系统自由度为:
|
图 2 大型风电增速器齿轮传动系统等效力学模型 Figure 2 Dynamic models of planetary transmission |
| $ \mathit{\boldsymbol{\delta }} = {\left( {u_{\rm{c}}^j,x_{\rm{c}}^j,y_{\rm{c}}^j,z_{\rm{c}}^j,u_{\rm{r}}^j,{\rm{u}}_{\rm{s}}^j,x_{\rm{s}}^j,y_{\rm{s}}^j,z_{\rm{s}}^j,u_{{\rm{p}}i}^j,\xi _{{\rm{p}}i}^j,\eta _{{\rm{p}}i}^j,z_{{\rm{p}}i}^j,{u_7},{y_7},{z_7},{u_8},{x_8},{y_8},{z_8}} \right)^{\rm{T}}}, $ | (1) |
其中x, y, z分别表示中心传动构件在各自定坐标系下沿坐标轴方向的振动位移,ξ, η分别表示行星轮在各自动坐标下的水平和垂直方向的振动位移, u表示传动构件扭转方向振动位移,u=rbθ,rb代表各齿轮基圆半径或行星架等效基圆半径。
1.1 构件相对位移1)太阳轮行星轮沿啮合线方向相对位移δjspi:
| $ \[\begin{array}{*{20}{c}} {\delta _{{\rm{sp}}i}^j = \cos {\beta ^j}\left[ {u_{{\rm{p}}i}^j - u_{\rm{s}}^j + \cos {\alpha ^j}u_{\rm{c}}^j + \left( {x_{\rm{s}}^j - x_{\rm{c}}^j} \right)\sin \left( { - \psi _i^j + {\alpha ^j}} \right) - } \right.}\\ {\left. {\left( {y_{\rm{s}}^j - y_{\rm{c}}^j} \right)\cos \left( { - \psi _i^j + {\alpha ^j}} \right) + \eta _{{\rm{p}}i}^j\cos {\alpha ^j} - \xi _{{\rm{p}}i}^j\sin {\alpha ^j}} \right] - e_{{\rm{sp}}i}^j\left( t \right)。} \end{array}\] $ | (2) |
2)内齿圈行星轮沿啮合线方向相对位移δrpij:
| $ \begin{array}{c} \delta _{{\rm{rp}}i}^j = \cos {\beta ^j}\left[ {u_{\rm{r}}^j} \right. + u_{\rm{c}}^j\cos {\alpha ^j} - u_{{\rm{p}}i}^j + x_{\rm{c}}^j\sin \left( {\psi _i^j + {\alpha ^j}} \right) + y_{\rm{c}}^j\cos \left( {\psi _i^j + {\alpha ^j}} \right) + \\ \left. {\xi _{{\rm{p}}i}^j\sin {\alpha ^j} + \eta _{{\rm{p}}i}^j\cos {\alpha ^j}} \right] - e_{{\rm{rp}}i}^j\left( t \right)。 \end{array} $ | (3) |
3)高速级齿轮沿啮合线方向总的相对位移δ78:
| $ {\delta _{78}} = \left[ {\left( {{u_7} - {u_8}} \right) + \left( {{y_7} - {y_8}} \right)\cos {\alpha _{{\rm{t78}}}} + \left( {{x_7} - {x_8}} \right)\sin {\alpha _{{\rm{t78}}}}} \right]\cos {\beta _{{\rm{b78}}}} - {e_{78}}\left( t \right)。 $ | (4) |
式(2)、(3)中, βj为第j级行星传动基圆螺旋角;αj为第j级行星传动的端面啮合角;ψij为第j级第i个行星轮在总体坐标系中的相位角,ψij=2π(i-1)/n,n为行星轮个数,输入级n=4, 中间级n=3;erpij(t)、espij(t)为第j级行星传动内、外啮合的啮合综合误差,见式(19);式(4)中, αt78为高速级齿轮端面压力角;βb78为高速级齿轮基圆螺旋角;e78(t)为高速级齿轮啮合综合误差。
1.2 系统动力学方程利用集中质量参数法及牛顿第二定律建立两级行星串联系统的动力学方程。
1)输入级行星架动力学方程:
| $ \left\{ \begin{array}{l} m_{{\rm{eqc}}}^{\rm{Ⅰ}}\ddot u_{\rm{c}}^{\rm{Ⅰ}} + K_{{\rm{oc}}}^{\rm{Ⅰ}}u_{\rm{c}}^{\rm{Ⅰ}} + C_{\rm{c}}^{\rm{Ⅰ}}\dot u_{\rm{c}}^{\rm{Ⅰ}} + \left[ {\sum\limits_{i = 1}^4 {\left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}}} \right) + } } \right.\\ \left. {\sum\limits_{i = 1}^4 {\left( {C_{{\rm{rp}}i}^{\rm{Ⅰ}}\delta _{{\rm{rp}}i}^{\rm{Ⅰ}} + K_{{\rm{rp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{rp}}i}^{\rm{Ⅰ}}} \right)} } \right]\cos {\beta ^{\rm{Ⅰ}}} = {T_{{\rm{in}}}}/r_{{\rm{bc}}}^{\rm{Ⅰ}},\\ m_{\rm{c}}^{\rm Ⅰ}\ddot x_{\rm{c}}^{\rm Ⅰ} + C_{\rm{c}}^{\rm{Ⅰ}}\dot x_{\rm{c}}^{\rm{Ⅰ}} + K_{\rm{c}}^{\rm{Ⅰ}}x_{\rm{c}}^{\rm{Ⅰ}} - \sum\limits_{i = 1}^4 {\left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}}} \right)\cos {\beta ^{\rm{Ⅰ}}}\sin \left( {{\alpha ^{\rm{Ⅰ}}} - \psi _i^{\rm{Ⅰ}}} \right) + } \\ \sum\limits_{i = 1}^4 {\left( {C_{{\rm{rp}}i}^{\rm Ⅰ}\delta _{{\rm{rp}}i}^{\rm{Ⅰ}} + K_{{\rm{rp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{rp}}i}^{\rm{Ⅰ}}} \right)\cos {\beta ^{\rm{Ⅰ}}}\sin \left( {{\alpha ^{\rm{Ⅰ}}} - \psi _i^{\rm{Ⅰ}}} \right) = 0,} \\ m_{\rm{c}}^{\rm{Ⅰ}}\ddot y_{\rm{c}}^{\rm{Ⅰ}} + C_{\rm{c}}^{\rm{Ⅰ}}\dot y_{\rm{c}}^{\rm{Ⅰ}} + K_{\rm{c}}^{\rm{Ⅰ}}y_{\rm{c}}^{\rm{Ⅰ}} + \sum\limits_{i = 1}^4 {\left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}}} \right)\cos {\beta ^{\rm{Ⅰ}}}\cos \left( {{\alpha ^{\rm{Ⅰ}}} - \psi _i^{\rm{Ⅰ}}} \right) + } \\ \sum\limits_{i = 1}^4 {\left( {C_{{\rm{rp}}i}^{\rm{Ⅰ}}\delta _{{\rm{rp}}i}^{\rm{Ⅰ}} + K_{{\rm{rp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{rp}}i}^{\rm{Ⅰ}}} \right)\cos {\beta ^{\rm{Ⅰ}}}\cos \left( {{\alpha ^{\rm{Ⅰ}}} + \psi _i^{\rm{Ⅰ}}} \right) = 0,} \\ m_{\rm{c}}^{\rm{Ⅰ}}\ddot z_{\rm{c}}^{\rm{Ⅰ}} + C_{\rm{c}}^{\rm{Ⅰ}}\dot z_{\rm{c}}^{\rm{Ⅰ}} + K_{\rm{c}}^{\rm{Ⅰ}}z_{\rm{c}}^{\rm{Ⅰ}} + \sum\limits_{i = 1}^4 {\left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}}} \right)\sin {\beta ^{\rm{Ⅰ}}} - } \\ \sum\limits_{i = 1}^4 {\left( {C_{{\rm{rp}}i}^{\rm{Ⅰ}}\delta _{{\rm{rp}}i}^{\rm{Ⅰ}} + K_{{\rm{rp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{rp}}i}^{\rm{Ⅰ}}} \right)\sin {\beta ^{\rm{Ⅰ}}} = 0。} \end{array} \right. $ | (5) |
2)输入级内齿圈动力学方程:
| $ m_{{\rm{eqr}}}^{\rm{Ⅰ}}\ddot u_r^{\rm{Ⅰ}} + C_{{\rm{or}}}^{\rm{Ⅰ}}\dot u_{\rm{c}}^{\rm{Ⅰ}} + K_{{\rm{or}}}^{\rm{Ⅰ}}u_{\rm{r}}^{\rm{Ⅰ}} + \sum\limits_{i = 1}^4 {\left( {C_{{\rm{rp}}i}^{\rm{Ⅰ}}\delta _{{\rm{rp}}i}^{\rm{Ⅰ}} + K_{{\rm{rp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{rp}}i}^{\rm{Ⅰ}}} \right)\sin {\beta ^{\rm{Ⅰ}}} = 0。} $ | (6) |
3)输入级太阳轮动力学方程:
| $ \left\{ \begin{array}{l} m_{{\rm{eqs}}}^{\rm{Ⅰ}}\ddot u_{\rm{s}}^{\rm{Ⅰ}} + {K_{{\rm{sc}}}}\left( {u_{\rm{s}}^{\rm{Ⅰ}} - u_{\rm{c}}^{{\rm{ⅠⅠ}}}} \right) - \sum\limits_{i = 1}^4 {\left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}}} \right)\cos {\beta ^{\rm{Ⅰ}}} = 0,} \\ m_{\rm{s}}^{\rm{Ⅰ}}\ddot x_{\rm{s}}^{\rm{Ⅰ}} + C_{\rm{s}}^{\rm{Ⅰ}}\dot x_{\rm{s}}^{\rm{Ⅰ}} + K_{\rm{s}}^{\rm{Ⅰ}}x_{\rm{s}}^{\rm{Ⅰ}} + \sum\limits_{i = 1}^4 {\left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}}} \right)} \cos {\beta ^{\rm{Ⅰ}}}\sin \left( {{\alpha ^{\rm{Ⅰ}}} - \psi _i^{\rm{Ⅰ}}} \right) = 0,\\ m_{\rm{s}}^{\rm{Ⅰ}}\ddot y_{\rm{s}}^{\rm{Ⅰ}} + C_{\rm{s}}^{\rm{Ⅰ}}\dot y_{\rm{s}}^{\rm{Ⅰ}} + K_{\rm{s}}^{\rm{Ⅰ}}y_{\rm{s}}^{\rm{Ⅰ}} - \sum\limits_{i = 1}^4 {\left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}}} \right)\cos {\beta ^{\rm{Ⅰ}}}\cos \left( {{\alpha ^{\rm{Ⅰ}}} - \psi _i^{\rm{Ⅰ}}} \right) = 0,} \\ m_{\rm{s}}^{\rm{Ⅰ}}\ddot z_{\rm{s}}^{\rm{Ⅰ}} + C_{\rm{s}}^{\rm{Ⅰ}}\dot z_{\rm{s}}^{\rm{Ⅰ}} + K_{\rm{s}}^{\rm{Ⅰ}}z_{\rm{s}}^{\rm{Ⅰ}} - \sum\limits_{i = 1}^4 {\left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}}} \right)\sin {\beta ^{\rm{Ⅰ}}} = 0。} \end{array} \right. $ | (7) |
4)输入级行星轮动力学方程:
| $ \left\{ \begin{array}{l} m_{{\rm{eqp}}i}^{\rm{Ⅰ}}\ddot u_{{\rm{p}}i}^{\rm{Ⅰ}} + \left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} - C_{{\rm{rp}}i}^{\rm{Ⅰ}}\delta _{{\rm{rp}}i}^{\rm{Ⅰ}} - K_{{\rm{rp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{rp}}i}^{\rm{Ⅰ}}} \right)\cos {\beta ^{\rm{Ⅰ}}} = 0,\\ m_{{\rm{p}}i}^{\rm{Ⅰ}}\xi _{{\rm{p}}i}^{\rm{Ⅰ}} - \left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} - C_{{\rm{rp}}i}^{\rm{Ⅰ}}\delta _{{\rm{rp}}i}^{\rm{Ⅰ}} - K_{{\rm{rp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{rp}}i}^{\rm{Ⅰ}}} \right)\\ \cos {\beta ^{\rm{Ⅰ}}}\sin {\alpha ^{\rm{Ⅰ}}} + C_{{\rm{p}}i}^{\rm{Ⅰ}}\xi _{{\rm{p}}i}^{\rm{Ⅰ}} + K_{{\rm{p}}i}^{\rm{Ⅰ}}\xi _{{\rm{p}}i}^{\rm{Ⅰ}} = 0,\\ m_{{\rm{p}}i}^{\rm{Ⅰ}}\dot \eta _{{\rm{p}}i}^{\rm{Ⅰ}} + \left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + C_{{\rm{rp}}i}^{\rm{Ⅰ}}\delta _{{\rm{rp}}i}^{\rm{Ⅰ}} + K_{{\rm{rp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{rp}}i}^{\rm{Ⅰ}}} \right)\\ \cos {\beta ^{\rm{Ⅰ}}}\cos {\alpha ^{\rm{Ⅰ}}} + C_{{\rm{p}}i}^{\rm{Ⅰ}}\dot \eta _{{\rm{p}}i}^{\rm{Ⅰ}} + K_{{\rm{p}}i}^{\rm{Ⅰ}}\eta _{{\rm{p}}i}^{\rm{Ⅰ}} = 0,\\ m_{{\rm{p}}i}^{\rm{Ⅰ}}\ddot z_{{\rm{p}}i}^{\rm{Ⅰ}} + \left( {C_{{\rm{sp}}i}^{\rm{Ⅰ}}\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} + K_{{\rm{sp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{sp}}i}^{\rm{Ⅰ}} - C_{{\rm{rp}}i}^{\rm{Ⅰ}}\delta _{{\rm{rp}}i}^{\rm{Ⅰ}} - K_{{\rm{rp}}i}^{\rm{Ⅰ}}\left( t \right)\delta _{{\rm{rp}}i}^{\rm{Ⅰ}}} \right)\\ \sin {\beta ^{\rm{Ⅰ}}} + C_{{\rm{p}}i}^{\rm{Ⅰ}}\dot z_{{\rm{p}}i}^{\rm{Ⅰ}} + K_{{\rm{p}}i}^{\rm{Ⅰ}}z_{{\rm{p}}i}^{\rm{Ⅰ}} = 0。 \end{array} \right. $ | (8) |
5)中间级行星架动力学方程:
| $ \left\{ \begin{array}{l} m_{{\rm{eqc}}}^{{\rm{Ⅱ}}}\ddot u_{\rm{c}}^{{\rm{Ⅱ}}} + {K_{{\rm{sc}}}}\left( {u_{\rm{c}}^{{\rm{Ⅱ}}} - u_{\rm{s}}^{\rm{Ⅰ}}} \right) + \left[ {\sum\limits_{i = 1}^3 {\left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}}} \right)} } \right.\\ \left. { + \sum\limits_{i = 1}^3 {\left( {C_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}}} \right)} } \right]\cos {\beta ^{{\rm{Ⅱ}}}} = 0,\\ m_{\rm{c}}^{{\rm{Ⅱ}}}\ddot x_{\rm{c}}^{{\rm{Ⅱ}}} + C_{\rm{c}}^{{\rm{Ⅱ}}}\dot x_{\rm{c}}^{{\rm{Ⅱ}}} + K_{\rm{c}}^{{\rm{Ⅱ}}}x_{\rm{c}}^{{\rm{Ⅱ}}} - \sum\limits_{i = 1}^3 {\left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}}} \right)} \\ \cos {\beta ^{{\rm{Ⅱ}}}}\sin \left( {{\alpha ^{{\rm{Ⅱ}}}} - \psi _i^{{\rm{Ⅱ}}}} \right) + \\ \sum\limits_{i = 1}^3 {\left( {C_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}}} \right)\cos {\beta ^{{\rm{Ⅱ}}}}\sin \left( {{\alpha ^{{\rm{Ⅱ}}}} + \psi _i^{{\rm{Ⅱ}}}} \right) = 0,} \\ m_{\rm{c}}^{{\rm{Ⅱ}}}\ddot y_{\rm{c}}^{{\rm{Ⅱ}}} + C_{\rm{c}}^{{\rm{Ⅱ}}}\dot y_{\rm{c}}^{{\rm{Ⅱ}}} + K_{\rm{c}}^{{\rm{Ⅱ}}}y_{\rm{c}}^{{\rm{Ⅱ}}} + \sum\limits_{i = 1}^3 {\left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}}} \right)} \\ \cos {\beta ^{{\rm{Ⅱ}}}}\cos \left( {{\alpha ^{{\rm{Ⅱ}}}} - \psi _i^{{\rm{Ⅱ}}}} \right) + \\ \sum\limits_{i = 1}^3 {\left( {C_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}}} \right)\cos {\beta ^{{\rm{Ⅱ}}}}\cos \left( {{\alpha ^{{\rm{Ⅱ}}}} + \psi _i^{{\rm{Ⅱ}}}} \right) = 0,} \\ m_{\rm{c}}^{{\rm{Ⅱ}}}\ddot z_{\rm{c}}^{{\rm{Ⅱ}}} + C_{\rm{c}}^{{\rm{Ⅱ}}}\dot z_{\rm{c}}^{{\rm{Ⅱ}}} + K_{\rm{c}}^{{\rm{Ⅱ}}}z_{\rm{c}}^{{\rm{Ⅱ}}} + \sum\limits_{i = 1}^3 {\left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}}} \right)\sin {\beta ^{{\rm{Ⅱ}}}}} \\ - \sum\limits_{i = 1}^3 {\left( {C_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}}} \right)\sin {\beta ^{{\rm{Ⅱ}}}} = 0.} \end{array} \right. $ | (9) |
6)中间级内齿圈动力学方程:
| $ m_{{\rm{eqr}}}^{{\rm{Ⅱ}}}\ddot u_r^{{\rm{Ⅱ}}} + C_{{\rm{or}}}^{{\rm{Ⅱ}}}\dot u_{\rm{r}}^{{\rm{Ⅱ}}} + K_{{\rm{or}}}^{{\rm{Ⅱ}}}u_{\rm{r}}^{{\rm{Ⅱ}}} + \sum\limits_{i = 1}^3 {\left( {C_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}}} \right)} \cos {\beta ^{{\rm{Ⅱ}}}} = 0, $ | (10) |
7)中间级太阳轮动力学方程:
| $ \left\{ \begin{array}{l} m_{{\rm{eqs}}}^{{\rm{Ⅱ}}}u_{\rm{s}}^{{\rm{Ⅱ}}} + {K_{{\rm{s7}}}}\left( {u_{\rm{s}}^{{\rm{Ⅱ}}} - {u_7}} \right) - \sum\limits_{i = 1}^3 {\left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}}} \right)\cos {\beta ^{{\rm{Ⅱ}}}} = 0,} \\ m_{\rm{s}}^{{\rm{Ⅱ}}}\ddot x_{\rm{s}}^{{\rm{Ⅱ}}} + C_{\rm{s}}^{{\rm{Ⅱ}}}\dot x_{\rm{s}}^{{\rm{Ⅱ}}} + K_{\rm{s}}^{{\rm{Ⅱ}}}x_{\rm{s}}^{{\rm{Ⅱ}}} + \sum\limits_{i = 1}^3 {\left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}}} \right)} \\ \cos {\beta ^{{\rm{Ⅱ}}}}\sin \left( {{\alpha ^{{\rm{Ⅱ}}}} - \psi _i^{{\rm{Ⅱ}}}} \right) = 0,\\ m_{\rm{s}}^{{\rm{Ⅱ}}}\ddot y_{\rm{s}}^{{\rm{Ⅱ}}} + C_{\rm{s}}^{{\rm{Ⅱ}}}\dot y_{\rm{s}}^{{\rm{Ⅱ}}} + K_{\rm{s}}^{{\rm{Ⅱ}}}y_{\rm{s}}^{{\rm{Ⅱ}}} + \sum\limits_{i = 1}^3 {\left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}}} \right)} \\ \cos {\beta ^{{\rm{Ⅱ}}}}\sin \left( {{\alpha ^{{\rm{Ⅱ}}}} - \psi _i^{{\rm{Ⅱ}}}} \right) = 0,\\ m_{\rm{s}}^{{\rm{Ⅱ}}}\ddot z_{\rm{s}}^{{\rm{Ⅱ}}} + C_{\rm{s}}^{{\rm{Ⅱ}}}\dot z_{\rm{s}}^{{\rm{Ⅱ}}} + K_{\rm{s}}^{{\rm{Ⅱ}}}z_{\rm{s}}^{{\rm{Ⅱ}}} - \sum\limits_{i = 1}^3 {\left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}}} \right)\sin {\beta ^{{\rm{Ⅱ}}}} = 0。} \end{array} \right. $ | (11) |
8)中间级行星轮动力学方程:
| $ \left\{ \begin{array}{l} m_{{\rm{eqp}}i}^{{\rm{Ⅱ}}}\ddot u_{{\rm{p}}i}^{{\rm{Ⅱ}}} + \left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} - C_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}} - K_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}}} \right)\cos {\beta ^{{\rm{Ⅱ}}}} = 0,\\ m_{{\rm{p}}i}^{{\rm{Ⅱ}}}\xi _{{\rm{p}}i}^{{\rm{Ⅱ}}} - \left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} - C_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}} - K_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}}} \right)\cos {\beta ^{{\rm{Ⅱ}}}}\\ \sin {\alpha ^{{\rm{Ⅱ}}}} + C_{{\rm{p}}i}^{{\rm{Ⅱ}}}\xi _{{\rm{p}}i}^{{\rm{Ⅱ}}} + K_{{\rm{p}}i}^{{\rm{Ⅱ}}}\xi _{{\rm{p}}i}^{{\rm{Ⅱ}}} = 0,\\ m_{{\rm{p}}i}^{{\rm{Ⅱ}}}\dot \eta _{{\rm{p}}i}^{{\rm{Ⅱ}}} + \left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + C_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}}} \right)\cos {\beta ^{{\rm{Ⅱ}}}}\\ \sin {\alpha ^{{\rm{Ⅱ}}}} + C_{{\rm{p}}i}^{{\rm{Ⅱ}}}\xi _{{\rm{p}}i}^{{\rm{Ⅱ}}} + K_{{\rm{p}}i}^{{\rm{Ⅱ}}}\xi _{{\rm{p}}i}^{{\rm{Ⅱ}}} = 0,\\ m_{{\rm{p}}i}^{{\rm{Ⅱ}}}\ddot z_{{\rm{p}}i}^{{\rm{Ⅱ}}} + \left( {C_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} + K_{{\rm{sp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{sp}}i}^{{\rm{Ⅱ}}} - C_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}} - K_{{\rm{rp}}i}^{{\rm{Ⅱ}}}\left( t \right)\delta _{{\rm{rp}}i}^{{\rm{Ⅱ}}}} \right)\cos {\beta ^{{\rm{Ⅱ}}}}\\ + C_{{\rm{p}}i}^{{\rm{Ⅱ}}}\dot z_{{\rm{p}}i}^{{\rm{Ⅱ}}} + K_{{\rm{p}}i}^{{\rm{Ⅱ}}}z_{{\rm{p}}i}^{{\rm{Ⅱ}}} = 0。 \end{array} \right. $ | (12) |
9)高速级大齿轮动力学方程:
| $ \left\{ \begin{array}{l} {m_{{\rm{eq}}7}}{{\ddot u}_7} + \left[ {{C_{78}}{\delta _{78}} + {K_{78}}\left( t \right){\delta _{78}}} \right]\cos {\beta _{{\rm{b}}78}} + {K_{{\rm{s}}7}}\left( {{u_7} - u_{\rm{s}}^{{\rm{Ⅱ}}}} \right) = 0,\\ {m_7}{{\ddot x}_7} + {C_7}{{\dot x}_7} + {K_7}{x_7} + \left[ {{C_{78}}{\delta _{78}} + {K_{78}}\left( t \right){\delta _{78}}} \right]\cos {\beta _{{\rm{b78}}}}\sin {\alpha _{{\rm{t78}}}} = 0,\\ {m_7}{{\ddot y}_7} + {C_7}{{\dot y}_7} + {K_7}{y_7} + \left[ {{C_{78}}{\delta _{78}} + {K_{78}}\left( t \right){\delta _{78}}} \right]\cos {\beta _{{\rm{b78}}}}\cos {\alpha _{{\rm{t78}}}} = 0,\\ {m_7}{{\ddot z}_7} + {C_7}{{\dot z}_7} + {K_7}{z_7} + \left[ {{C_{78}}{\delta _{78}} + {K_{78}}\left( t \right){\delta _{78}}} \right]\sin {\beta _{{\rm{b78}}}} = 0。 \end{array} \right. $ | (13) |
10)高速级小齿轮动力学方程:
| $ \left\{ \begin{array}{l} {m_{{\rm{eq8}}}}{{\ddot u}_8} - \left[ {{C_{78}}{\delta _{78}} + {K_{78}}\left( t \right){\delta _{78}}} \right]\cos {\beta _{{\rm{b78}}}} = - {T_{{\rm{out/}}}}{r_{{\rm{b8}}}},\\ {m_8}{{\ddot x}_8} + {C_8}{{\dot x}_8} + {K_8}{x_8} - \left[ {{C_{78}}{\delta _{78}} + {K_{78}}\left( t \right){\delta _{78}}} \right]\cos {\beta _{{\rm{b78}}}}\sin {\alpha _{{\rm{t}}78}} = 0,\\ {m_8}{{\ddot x}_8} + {C_8}{{\dot x}_8} + {K_8}{x_8} - \left[ {{C_{78}}{\delta _{78}} + {K_{78}}\left( t \right){\delta _{78}}} \right]\cos {\beta _{{\rm{b78}}}}\sin {\alpha _{{\rm{t}}78}} = 0,\\ {m_8}{{\ddot z}_8} + {C_8}{{\dot z}_8} + {K_8}{z_8} - \left[ {{C_{78}}{\delta _{78}} + {K_{78}}\left( t \right){\delta _{78}}} \right]\sin {\beta _{{\rm{b}}78}} = 0。 \end{array} \right. $ | (14) |
式(5)~(14)中的相关参数说明如下:
Kjrpi为第j级第i个行星轮与内齿圈之间的时变啮合刚度, 见式(17);Kjspi(t)为第j级第i个行星轮与太阳轮之间的时变啮合刚度, 见式(17);K78(t)为斜齿轮7与斜齿轮8之间的时变啮合刚度, 见式(20);Cjrpi为第j级第i个行星轮与内齿圈之间的粘性阻尼;Cjspi为第j级第i个行星轮与太阳轮之间的粘性阻尼;C78为斜齿轮7与斜齿轮8之间的粘性阻尼;Kjor, Kjoc为第j级内齿圈、行星架的扭转刚度;Cjor, Cjoc为第j级内齿圈、行星架的扭转阻尼;Ksc为两级行星传动间的串联扭转刚度;Ks7为中间级行星传动与高速级齿轮传动间的串联扭转刚度;Kjs, Kjpi分别表示太阳轮及行星轮第j级行星传动中的支承刚度;Cjs, Cjpi分别表示太阳轮及行星轮第j级行星传动中的支承阻尼;Tin, Tout为输入、输出转矩。
1.3 外部激励风力发电机齿轮传动系统输入端的转矩由外界的随机风速确定。因此选用双参数威布尔分布来模拟随机风速模型,以使其结果更加贴近风机增速器的实际工况, 如式(15)所示。
| $ f\left( v \right) = \left( {\frac{k}{c}} \right){\left( {\frac{v}{c}} \right)^{k - 1}}{e^{ - \left( {\frac{v}{c}} \right)k}},\left( {0 < v < \infty } \right)。 $ | (15) |
式中:v为风速,m/s;k为形状参数;c为尺度参数,m/s。依据风速的期望及方差表达式并进行近似计算可得到k及c的表达式分别为[12]:
| $ k = {\left( {\frac{{\sqrt {D\left( v \right)} }}{{E\left( v \right)}}} \right)^{ - 1.086}},c = \frac{{E\left( v \right)}}{{\Gamma \left( {1 + 1/k} \right)}}。 $ | (16) |
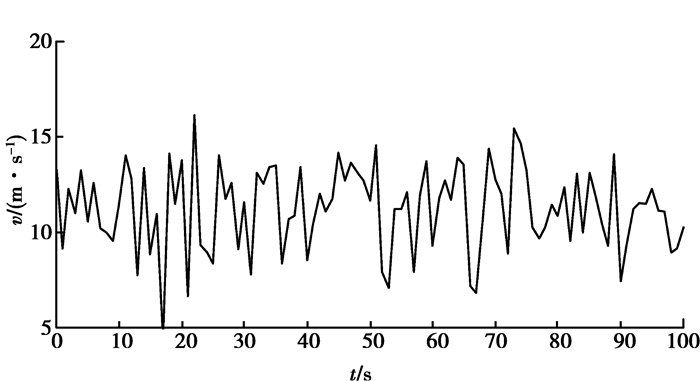
对于某大型风电增速器齿轮传动系统额定设计功率为3 300 kW,额定工作转速k为13 r/min,额定转矩Te为2 424 kN·m。所在风场平均风速为11 m/s,标准差为2.27 m/s。根据式(16)求得形状参数k为5.55,尺度参数c为11.908 9,利用双参数威布尔分布函数生成某100 s之内的随机风速时域模型,如图 3所示。
|
图 3 随机风速曲线图 Figure 3 Curve of random wind velocity |
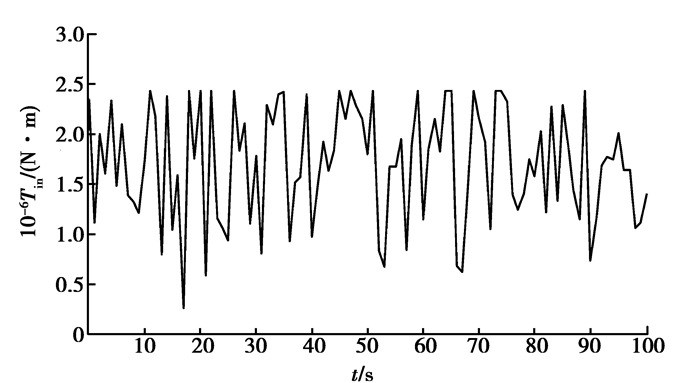
通过变桨距变速风力发电机齿轮箱的输入转矩和输入转速与风速之间的关系式[13],生成输入转矩曲线如图 4所示,以此作为外部激励。
|
图 4 输入转矩曲线图 Figure 4 Curve of input torque |
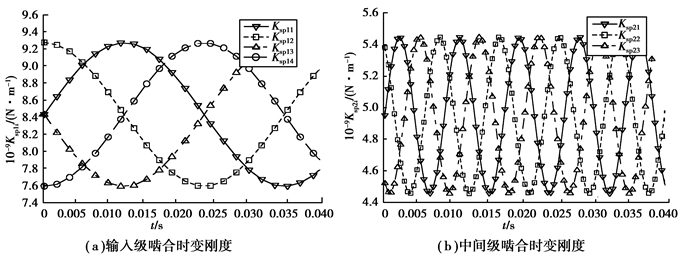
笔者将齿轮啮合刚度展开成傅里叶级数形式。为计算方便,进行分析时仅保留其啮合刚度的平均值项和第1阶谐波分量,如式(17)所示。以外啮合为例,得到的输入级和中间级的啮合刚度激励如图 5所示。
|
图 5 行星传动外啮合时变啮合刚度 Figure 5 Time-varying mesh stiffness of external mesh |
| $ \left\{ \begin{array}{l} {K_{{\rm{rp}}ji}}\left( t \right) = {{\bar k}_{{\rm{rp}}}}\left[ {1 + S\;\sin \left( {{\omega _{{\rm{m}}j}}t + {Z_r}{\psi _{ji}} + {\gamma _{{\rm{sr}}}}} \right)} \right],\\ {K_{{\rm{sp}}ji}}\left( t \right) = {{\bar k}_{{\rm{rp}}}}\left[ {1 + S\;\sin \left( {{\omega _{{\rm{m}}j}}t + {Z_s}{\psi _{ji}}} \right)} \right],\\ {K_{78}}\left( t \right) = {{\bar k}_{78}}\left[ {1 + S\;\sin \left( {{\omega _{{\rm{m78}}}}t} \right)} \right]。 \end{array} \right. $ | (17) |
式中:krp, kps, k78分别为行星传动内、外啮合及高速级齿轮啮合的平均啮合刚度;S为刚度幅值比,取0.2;γsr为行星轮系内外啮合相位差,行星轮齿数偶数时为0,奇数时为π;ωm为行星轮传动啮合齿频;Zs, Zr分别为太阳轮齿数及内齿圈齿数,ωmj为啮合频率,见式(18)。
| $ {\omega _{{\rm{m}}j}} = {Z_{{\rm{s}}j}}{Z_{{\rm{r}}j}}{\omega _{{\rm{s}}j}}/\left( {{Z_{{\rm{s}}j}} + {Z_{{\rm{r}}j}}} \right)。 $ | (18) |
研究齿轮系统动力学时可用齿轮切向总偏差表示齿轮传递误差,齿轮传递误差的时变性可近似成轴频和齿频谐波函数的叠加, 如式(19)所示[14]。
| $ e\left( t \right) = 0.5{F_{\rm{p}}}\sin \left( {2{\rm{\pi }}{\omega _{\rm{f}}}t + {\psi _{\rm{f}}}} \right) + 0.5f'{\;_{\rm{t}}}\sin \left( {2{\rm{\pi }}{\omega _{\rm{m}}}t + {\varphi _{\rm{m}}}} \right), $ | (19) |
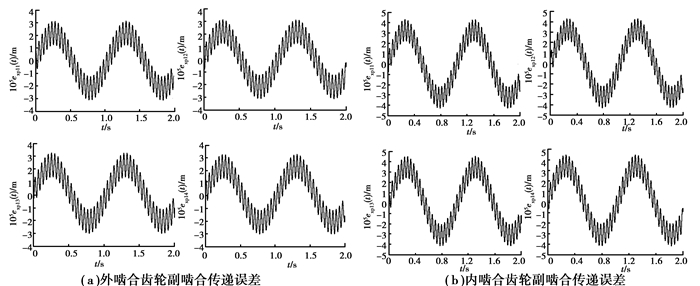
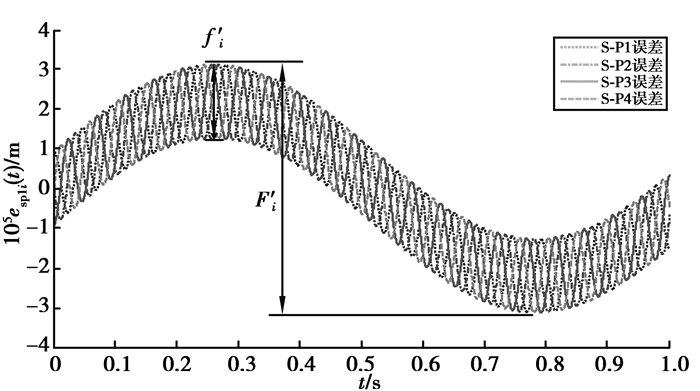
式中:e(t)为齿轮传递误差;ωf, ψf分别为齿轮转动频率(轴频)、初相位;ωm, φm分别为齿轮啮合频率、啮合初相位;Fp为行星轮系啮合齿距累积总偏差的幅值;ft′为单齿对切向偏差的幅值。根据式(19)可确定风电增速器两级行星轮系齿轮时变传递误差曲线如图 6所示。可见,内、外啮合的传递误差只有数值上的差异,变化规律相同,啮合传递误差的波动趋势是齿轮轴频和齿频相结合的结果,同一级行星传动中由于轴频相同,因此整体趋势一致,每个行星轮间由于相位的差异,在齿频的波动上略有差异,如图 7所示。
|
图 6 输入级行星轮系齿轮传递误差 Figure 6 Transfer errors of gears in 1st planetary transmission |
|
图 7 输入级各行星轮外啮合误差激励放大图 Figure 7 Detailed of external mesh transfer errors |
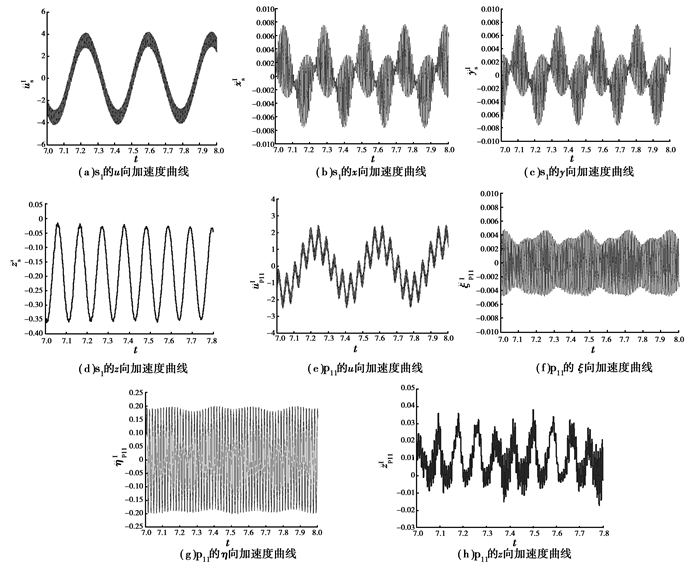
为了方便比较,将动力学方程组无量纲化后得到了各构件的振动加速度时域曲线,给出了第1级行星传动外啮合齿轮副的各自由度加速度曲线如图 8所示。由此可见,u方向振动位移明显大于径向及轴向位移,这是由于齿轮支承系统刚性大造成的,其中us1最大;在相同的振动方向上,太阳轮的振动位移总是大于行星轮,这说明在相同的啮合力作用下,直径越小变形越大,即各项线位移幅度越大。振动构件的加速度大小直接影响齿轮传动系统动态性能的好坏,降低振动加速度也是对传动系统减振降噪的主要途径。
|
图 8 第1级行星传动外啮合齿轮副各向量纲一的加速度 Figure 8 Accelerations of external mesh gears in 1st planetary transmisson |
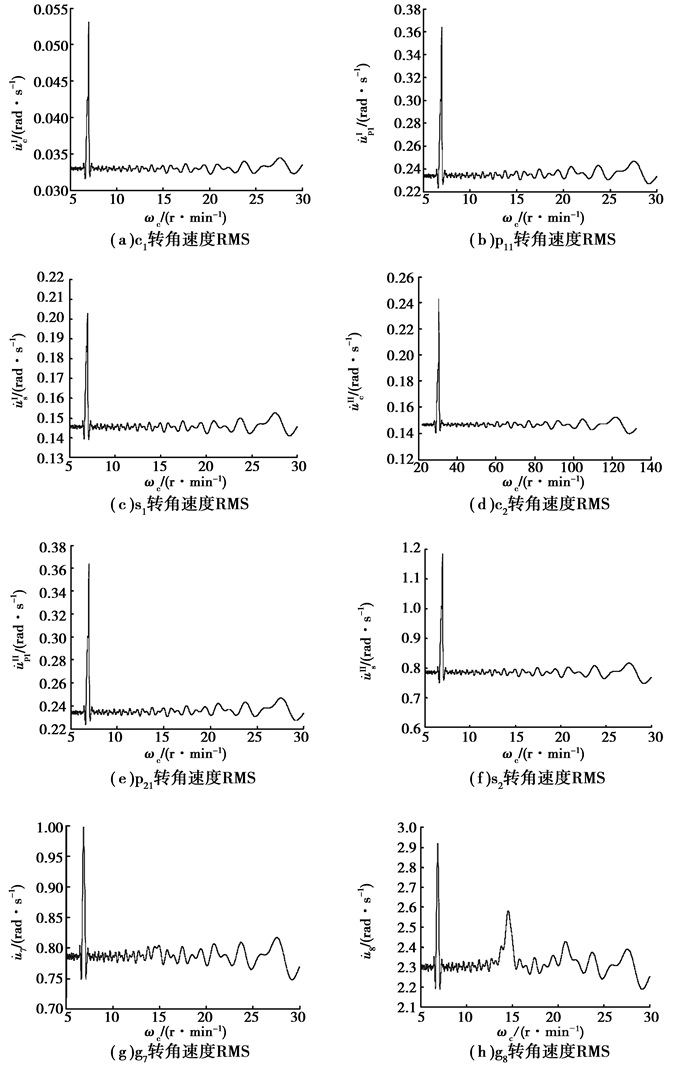
为合理确定传动系统的工况运行参数,对系统的不同输入转速条件下的振动情况进行分析是必须的。输入级行星架的输入转速可在0~30 r/min,基于数值计算仿真,得到了传动系统各构件在不同输入转速下的振动速度均方根值(root mean square, RMS)响应曲线如图 9所示。从图 9可以看出各构件振动响应随着输入行星架转速变化的波动情况,在某些输入转速下系统构件的振动速度会突然增大,如6.96、14.56、20.82和27.58 r/min。这是由于齿侧间隙等非线性因素造成的系统不稳定现象,工作过程中应尽量避开这些转速值及其附近的转速值,避开这些振动响应峰值,可以有效降低系统的振动,使系统保持稳定的状态。
|
图 9 不同输入转速下的RMS响应曲线 Figure 9 Curve of RMS response with different rotating speeds |
根据上节中行星轮系动态性能的分析及风机传动系统的结构特点,以系统最大加速度值作为评价系统动态性能的指标,选取两行星级的太阳轮、行星轮和高速级从动轮的扭转加速度的峰值作为动态优化目标,以系统体积作为静态优化目标。通过线性加权法将各分目标函数统一量纲处理后叠加起来,如式(20)所示。
| $ f = {\lambda _{{\rm{v1}}}}{f_{{\rm{v1}}}} + {\lambda _{{\rm{v2}}}}{f_{{\rm{v2}}}} + {\lambda _{{\rm{v3}}}}{f_{{\rm{v3}}}} + {\lambda _{{\rm{s1}}}}{f_{{\rm{s1}}}} + {\lambda _{{\rm{p1}}}}{f_{{\rm{p1}}}} + {\lambda _{{\rm{s2}}}}{f_{{\rm{s2}}}} + {\lambda _{{\rm{p2}}}}{f_{{\rm{p2}}}} + {\lambda _{{\rm{g8}}}}{f_{{\rm{g8}}}}, $ | (20) |
式中:fv1、fv2、fv3分别为第1级、第2级、高速级体积分目标函数,见式(21);fs1、fp1、fs2、fp2、fg8分别为第1级行星传动的太阳轮、行星轮、第2级行星传动的太阳轮、行星轮和高速级从动轮扭转振动加速度峰值分目标函数;λv1、λv2、λv3、λs1、λp1、λs2、λp2、λg8为相应的加权系数,需经过多次试运算来确定。最终确定体积加权系数均取为0.1;扭转加速度加权系数均取为0.14。
| $ \left\{ \begin{array}{l} {f_{{\rm{v1}}}} = {\rm{\pi }}{b^{\rm{I}}}\frac{{\left( {d_{{\rm{as1}}}^2 + 4d_{{\rm{ap1}}}^2 + d_{{\rm{fr1}}}^2 - d_{{\rm{ar1}}}^2} \right)}}{4},\\ {f_{{\rm{v2}}}} = {\rm{\pi }}{b^{{\rm{II}}}}\frac{{\left( {d_{{\rm{as2}}}^2 + 3d_{{\rm{ap2}}}^2 + d_{{\rm{fr2}}}^2 - d_{{\rm{ar2}}}^2} \right)}}{4},\\ {f_{{\rm{v3}}}} = \frac{{{\rm{\pi }}{b^{{\rm{III}}}}\left( {d_{{\rm{a7}}}^2 + d_{{\rm{a8}}}^2} \right)}}{{\rm{4}}}。 \end{array} \right. $ | (21) |
式中:daκ(κ=s1, p1, r1, s2, p2, r2, 7, 8)为各齿轮的齿顶圆直径;dfrj为第j级行星传动的内齿圈齿根圆直径。
本文的设计变量x定义为齿数、模数、螺旋角和齿宽、法向变位系数及啮合角,如式(22)所示。
| $ \mathit{\boldsymbol{x = }}{\left[ \begin{array}{l} Z_{\rm{s}}^{\rm{I}},\;\;m_{\rm{n}}^{\rm{I}},\;\;{b^{\rm{I}}},\;\;{\beta ^{\rm{I}}},\;\;x_{{\rm{ns}}}^{\rm{I}},\;\;\alpha _{{\rm{ps}}}^{\rm{I}},\;\;Z_{\rm{s}}^{{\rm{II}}},\;\;m_{\rm{n}}^{{\rm{II}}},\;\;{b^{{\rm{II}}}},\\ {\beta ^{{\rm{II}}}},\;\;x_{{\rm{ns}}}^{{\rm{II}}},\;\;\alpha _{{\rm{ps}}}^{{\rm{II}}},\;\;{Z_8},\;\;{m_{{\rm{n}}8}},\;\;{b^{{\rm{III}}}},\;\;{\beta _{78}},\;\;{x_{{\rm{n8}}}},\;\;{\alpha _{78}} \end{array} \right]^{\rm{T}}}。 $ | (22) |
本文所涉及的约束条件选为静态约束条件,包括传动条件、几何约束及可靠性约束条件[15],选取MATLAB优化工具箱中的fmincon函数进行求解,得到的参数优化后的结果如表 2所示, 括号中字母或数字表示构件名称。
| 表 1 设计变量原始参数 Table 1 Primitive design parameters |
| 表 2 设计变量优化结果 Table 2 Design parameters of optimization |
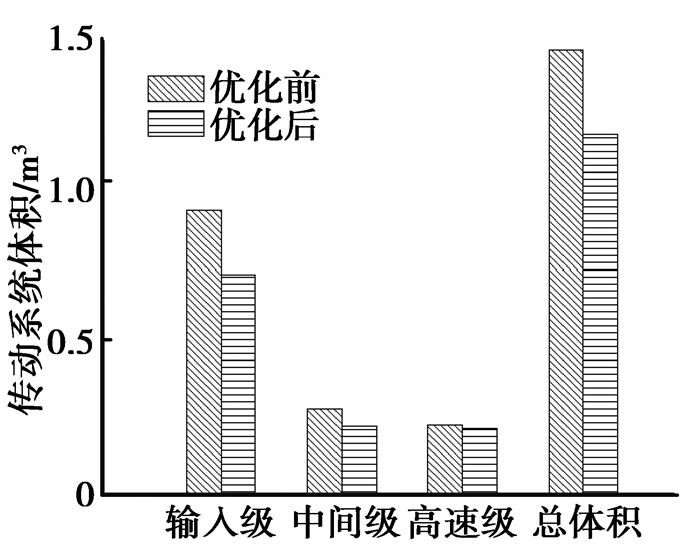
图 10为体积优化前后的对比,可见,每一级的齿轮传动系统体积都有所减小,减小幅度分别为:第1级22.12%,第2级19.97%,高速级5.1%,系统总体积降低了18.95%,实现了系统轻量化。
|
图 10 优化前后的体积对比 Figure 10 Volume comparison between system before and after optimization |
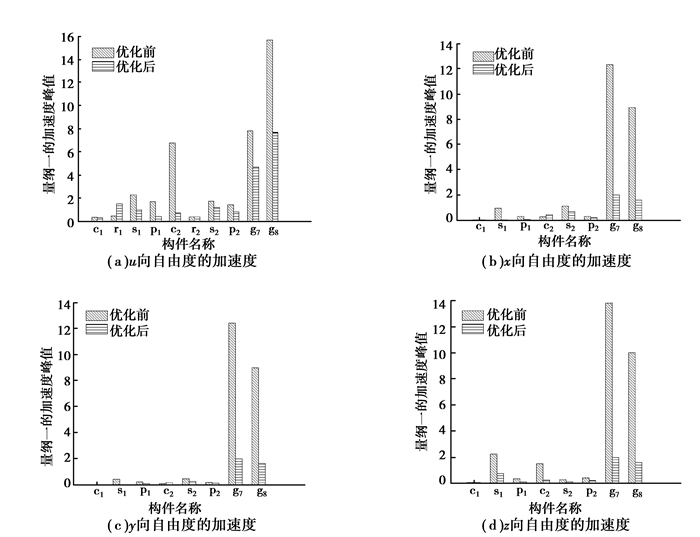
图 11为各构件自由度加速度优化前后的对比图,由图 11可见,优化前,各构件扭转方向的加速度最大,是引起传动系统振动的主要原因(见图 11(a));优化后绝大部分构件的振动加速度峰值有不同程度的减小(除内齿圈外,由于其本身优化前后的加速度都较小,因此此结果对整体动态性能影响不大),尤其对于动态特性较差的高速级齿轮,降低的幅度非常明显,从而达到了减振降噪的效果。
|
图 11 各构件优化前后加速度对比 Figure 11 Acceleration comparison between gears before and after optimization |
笔者通过建立大功率风机增速器齿轮传动系统动力学模型,研究其动态特性,并以此作为基础进行多目标优化设计,得到如下结论:
1)风机增速器齿轮传动系统各构件振动响应随着输入转速变化有所波动,在工况选择时应避开振动响应峰值以保证系统的稳定性及可靠性。
2)两级行星齿轮传动系统由于其结构的平衡作用,振动明显小于高速级齿轮,其扭转方向的振动大于径向及轴向自由度;高速级齿轮传动由于转速大、受载大而不均,使得其动态性能较行星传动差。
3)在对齿轮传动系统进行多目标动态优化后,在保证了可靠度与强度的要求前提下,不仅使大部分构件自由度加速度得到明显降低,而且使系统整体质量有一定程度的减少,达到了轻量化和减振降噪的目的,为齿轮传动设计提供理论依据。
| [1] | Kahraman A. Planetary gear train dynamics[J]. Journal of Mechanical Design, 1994, 116(3): 713–720. DOI:10.1115/1.2919441 |
| [2] | Parker R G, Agashe V, Vijayakar S M. Dynamic response of a planetary gear system using a finite element/contact mechanics model[J]. Journal of Mechanical Design, 2000, 122(3): 304–310. DOI:10.1115/1.1286189 |
| [3] | Parker R G. A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration[J]. Journal of Sound and Vibration, 2000, 236(4): 561–573. DOI:10.1006/jsvi.1999.2859 |
| [4] | Peeters J L M, Vandepitte D, Sas P. Analysis of internal drive train dynamics in a wind turbine[J]. Wind Energy, 2006, 9(1/2): 141–161. |
| [5] | Wei S, Chang W K, Chung C W, et al. Dynamic modeling and analysis of a wind turbine drivetrain using the torsional dynamic model[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(1): 153–159. DOI:10.1007/s12541-013-0021-2 |
| [6] |
卜忠红, 刘更, 吴立言.
行星齿轮传动动力学研究进展[J]. 振动与冲击, 2010, 29(9): 161–166.
BU Zhonghong, LIU Geng, WU Liyan. Research advances in planetary gear trains dynamics[J]. Journal of Vibration and Shock, 2010, 29(9): 161–166. (in Chinese) |
| [7] | Thompson D F, Gupta S, Shukla A. Tradeoff analysis in minimum volume design of multi-stage spur gear reduction units[J]. Mechanism and Machine Theory, 2000, 35(5): 609–627. DOI:10.1016/S0094-114X(99)00036-1 |
| [8] |
李武, 聂松辉, 陈方述.
基于遗传算法的风力发电行星传动系统多目标模糊优化[J]. 机械科学与技术, 2012, 31(11): 1801–1805.
LI Wu, NIE Songhui, CHEN Fangshu. Multi-objective fuzzy optimization for planetary transmission system of wind turbine based on genetic algorithms[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(11): 1801–1805. (in Chinese) |
| [9] |
刘景军.
基于改进型遗传算法的齿轮动态性能优化设计[J]. 武汉工程职业技术学院学报, 2003, 15(1): 6–9.
LIU Jingjun. Optimization design of gearing's dynamic performance based on iaga[J]. Journal of Wuhan Engineering Institute, 2003, 15(1): 6–9. (in Chinese) |
| [10] |
秦大同, 古西国, 王建宏, 等.
兆瓦级风力机齿轮传动系统动力学分析与优化[J]. 重庆大学学报, 2009, 32(4): 408–414.
QIN Datong, GU Xiguo, WANG Jianhong, et al. Dynamic analysis and optimization of gear trains in a megawatt level wind turbine[J]. Journal of Chongqing University, 2009, 32(4): 408–414. (in Chinese) |
| [11] |
秦大同, 邢子坤, 王建宏.
基于动力学和可靠性的风力发电齿轮传动系统参数优化设计[J]. 机械工程学报, 2008, 44(7): 24–31.
QIN Datong, XING Zikun, WANG Jianhong. Optimization design of system parameters of the gear transmission of wind turbine based on dynamics and reliability[J]. Chinese Journal of Mechanical Engineering, 2008, 44(7): 24–31. (in Chinese) |
| [12] |
李冬冬, 陈陈.
风力发电系统动态仿真的风速模型[J]. 中国电机工程学报, 2005, 25(21): 41–44.
LI Dongdong, CHEN Chen. Wind speed model for dynamic simulation of wind power generation system[J]. Proceedings of the Chinese Society for Electrical Engineering, 2005, 25(21): 41–44. (in Chinese) |
| [13] | 叶杭治. 风力发电机组的控制技术[M]. 北京: 机械工业出版社, 2006. |
| [14] | Wei J, Lv C, Sun W, et al. A study on optimum design method of gear transmission system for wind turbine[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(5): 767–778. DOI:10.1007/s12541-013-0100-4 |
| [15] | 叶元烈. 机械优化理论与设计[M]. 北京: 中国计量出版社, 2001. |
 2015, Vol. 38
2015, Vol. 38

