随着国内外风力发电的快速发展, 对风电设备的可靠性要求越来越高,对风电齿轮箱的要求也越来越高。风电齿轮箱作为风力发电系统的重要部件, 其性能和可靠性决定了整机系统的可靠性[1]。个别设计寿命为20年的风电齿轮箱仅使用几年就出现齿轮失效。风电齿轮失效的原因有很多种,其中早期的齿面微点蚀引起的失效已引起足够的重视。国际标准化组织ISO, 美国齿轮协会AGMA等均相继对微点蚀现象进行了一系列相关的专题研究, 取得了一定进展[2-6]。2010年ISO组织发布了微点蚀计算的技术报告《ISO/TR 15144-1:2010关于直齿斜齿的微点蚀承载能力计算》技术报告并首次提到微点蚀安全系数的计算方法[7]。风机的主要设计认证参考规范(GL规范)也已经把该安全系数做了明确的规定[8]。但国内还未见相关规范、设计手册对微点蚀计算有所涉及[4]。
微点蚀由在处于弹流润滑或边界润滑状态下的滚动和滑动接触赫兹压力引起的。微点蚀受载荷、速度、温度、表面状况、相对油膜厚度和润滑油的添加剂等影响而且通常发生在硬齿面上。微点蚀一般发生在低速重载齿轮上, 例如船用齿轮箱、风电齿轮箱的低速级齿轮啮合齿面及轴承。微点蚀始于一些非常微小的表面裂纹, 小裂纹继续扩展产生微点蚀,深度约10~20 μm,微点蚀可能融合后产生连续的断裂表面,肉眼可见的凹坑和麻点等。微点蚀可能被抑制,但一旦微点蚀继续扩展,将会降低齿面粗糙度,增加动载荷和噪音,并且可能发展成点蚀或其他形式的失效[7-11]。
渐开线齿轮可以简化为线接触弹流润滑问题[12-13]。ISO/TR 15144-1最小油膜厚度采用Dowson/Higginson拟合的计算公式,文中将采用由热弹流分析得到的最小油膜厚度。应用Matlab软件,以稳态线接触热弹流润滑数值计算为基础,直接计算出最小油膜厚度,然后进行微点蚀安全系数计算。对渐开线齿轮进行热弹流分析,分析不同啮合点的压力、膜厚、温升,为提高微点蚀强度提供理论依据及计算方法。
1 数学模型热弹流计算假设齿面不接触,而且齿面间流动处于层流状态,轴承压力p和厚度方向无关,润滑油为Newton流体。稳态的热弹流润滑分析程序所使用的基本方程以下章节给予介绍。
1.1 Reynolds方程根据杨沛然[14]的研究,稳态线接触热弹流理论中,对于Newton流体的广义雷诺方程可以简化为
| ∂∂x[(ρη)eh3∂p∂x]=12U∂(ρ∗h)∂x, |
式中:
| {p(s1)=p(s2)=0,p≥0(s1<x<x2)。 |
积分下线s1理论上应为-∞,但求解时常用绝对值足够大的常数如-5b(b为赫兹接触半宽)来代替,s2取计算域的最后一个节点。
1.2 膜厚方程水膜厚方程由几何膜厚和弹性变形构成,为
| h(x)=h0+x22R−2πE′∫s2s1p(s)ln(x−s)2ds, |
式中:R=1/(1/R1-1/R2),R1、R2为齿面的曲率; E′=2/[(1-v12)/E1+(1-v22)/E2],E1、E2,v1、v2分别为齿轮副的弹性模量和泊松比;h0为一未知参数,在求解过程中得到。
1.3 粘度和密度方程润滑油的密度、粘度采用ISO/TR 15144-1经验公式计算[7]为
| ρ=ρ15[1−0.7(T−15)ρ15], |
| lg(lg(106⋅η/ρ+0.7))=Alg(T)+B。 |
式中:ρ15为环境密度;A、B为参数,由40 ℃和100 ℃的粘度计算得出。
1.4 能量方程油膜的能量方程为
| c(ρu∂T∂z−q∂T∂z)−k∂2T∂z2=−Tρ∂ρ∂Tu∂p∂x+τ∂u∂z, |
式中:
油膜的流速计算公式为
| u=Ua+(∫z0z′dz′η−ηeη′eh∫z0dz′η)∂p∂x+ηe(Ub−Ua)η∫z0dzη, |
油膜速度梯度方程为
| ∂u∂x=1η(z−ηeη′eh)∂p∂x+ηe(Ub−Ua)ηh, |
齿轮的能量方程为
| {caρaUa∂T/∂x=ka∂2T/∂z2a,cbρbUb∂T/∂x=kb∂2T/∂z2b, |
式中:ρ、c和k分别为比热、密度和热传导系数;下标a和b用于区分大小齿轮;za、zb与z同向,是齿轮和油膜厚度方向的坐标。
固体温度和油膜温度在齿面上应是连续的,应满足界面热流量连续条件为
| {k∂T∂z=ka∂T∂za(在界面a上),k∂T∂z=kb∂T∂zb(在界面b上)。 |
上游逆流区和下游是不需要边界条件的,油膜上游的温度边界条件为
| T(s1,z)=T0(asdu(s1,z)≥0)。 |
轴和轴承内部的温度边界条件为
| T|za=−d=T0,T|zb=d=T0, |
d为变温层的深度。
1.5 载荷方程载荷方程为
| ω=∫s2s1pdx, |
式中:w为单位长度上施加的载荷。
2 数值方法文中选用多重网格法对上述方程进行求解。多重网格法可以增加收敛速度。数值分析过程为:首先方程无量纲化,求解区域划分网格,将方程离散,然后进行不考虑温度的弹流润滑方程求解,收敛后把弹流润滑的解作为热弹流润滑分析的初值进行最终的热弹流润滑分析[14-16]。程序采用6层网络及W循环,最稀疏层有41个节点。压力迭代采用文献[14]中的Gauss-Seidel迭代法。齿面间的润滑油区域z向共10个节点,齿轮区域z向共14个节点,温度场在最稠密层和最稀疏层计算,温度场的初值由弹流润滑后的最稀疏层计算得到,然后插值到最稠密层。经反复调整各低松弛因子,使所采用的数值算法能够快速收敛。通过不同的参数进行验证,证实上述方法能够收敛到唯一值。
3 结果分析ISO/TR 15144-1提供两种计算接触压力的方法:方法A基于齿面受载接触分析(LTCA), 可用一些商用软件计算,如LDP、LVR、Kisssoft、MASTA等; 方法B是简化的公式计算。文中两种方法没有区别,因为压力对热弹流润滑分析相是输入值。与ISO/TR 15144-1所给例子相同,计算油膜厚度时文中采用方法B,用FZG C-GF/8.3/90测试齿轮计算许用油膜厚度时采用方法A[9]。
为了确保计算结果的正确性, 先对程序进行了验证, 把粘度和密度方程改成与文献[14, 16]中一致,其计算结果与文献[14, 16]的结果基本吻合。
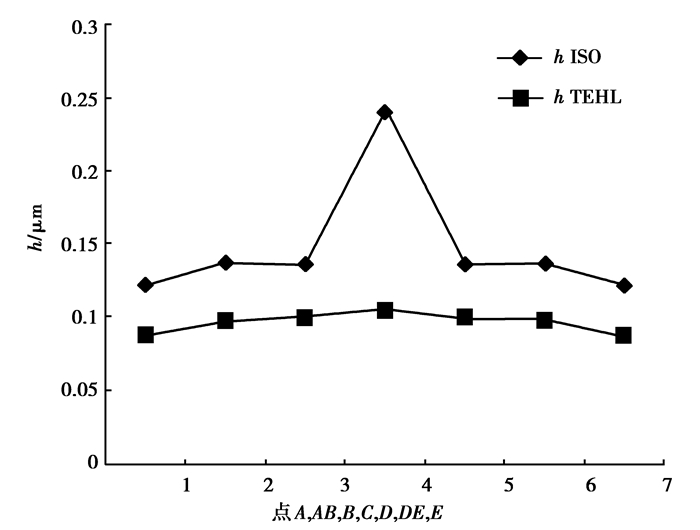
图 1为使用热弹流润滑分析得到的最小油膜厚度与使用ISO/TR 15144-1中的Dowson/Higginson公式计算的油膜厚度对比图。计算相关的齿轮参数、运行参数、材料参数和润滑油参数均与ISO/TR 15144-1附录B中的例子相同。图中,A, AB, B, C, D, DE, E为各啮合点,其中AB点为A点和B点的中点,DE点为D点和E点中点。由图可知:两种方法计算的油膜厚度趋势基本相同;采用热弹流润滑分析得到的最小油膜厚度显著低于使用ISO/TR 15144-1计算的油膜厚度;使用ISO/TR 15144-1计算的C点的油膜厚度显著高于其他点,主要是由于ISO/TR 15144-1计算的其他各点的局部闪温显著高于C点的局部闪温。C点相对滑移速度为0,显著小于其他各点,按ISO/TR 15144-1计算的C点局部闪温(为0 ℃)与其他各啮合点差异较大(其他各点都在100 ℃以上,详见ISO/TR 15144-1[7]附录B),导致油膜较厚。使用热弹流润滑分析得出的各点最小油膜厚度变化较平缓,没有出现节点C最小油膜厚度大幅增加,主要是由于通过热弹流润滑分析得出的各点温升小于ISO/TR 15144-1计算出来的各点温升;而且热弹流润滑分析得出的各点温升不如ISO/TR 15144-1计算的温升显著,各啮合点温升差异较小。
|
图 1 各啮合点最小油膜厚度 Figure 1 Local lubricant film thicknesses of main contact point |
风电齿轮箱中,低速级行星轮系,速度低、载荷大,因此微点蚀风险高于其他级别。文中将对有代表性的低速级行星轮和太阳轮的齿面进行分析。某2 MW机型齿轮箱计算相关参数如表 1所示,齿轮没有修形。润滑油为PAO基础油,采用FVA-FZG微点蚀测试(C-GF/8.3/90, Ra=0.5 μm)失效载荷等级SKS为10。该测试齿轮副最小油膜厚度始终为A点。SKS=10时,A点赫兹接触应力为1 476.2 MPa,输入扭矩为265.1 N·m[9]。
| 表 1 计算参数 Table 1 Parameters |
上述风电2 MW齿轮箱的最小油膜厚度和微点蚀安全系数如图 2、图 3所示;油膜形状和压力分布见图 4、图 5所示;C点及油膜最薄的啮合点A点温度升见图 6、图 7所示。微点蚀安全系数[7]定义为
|
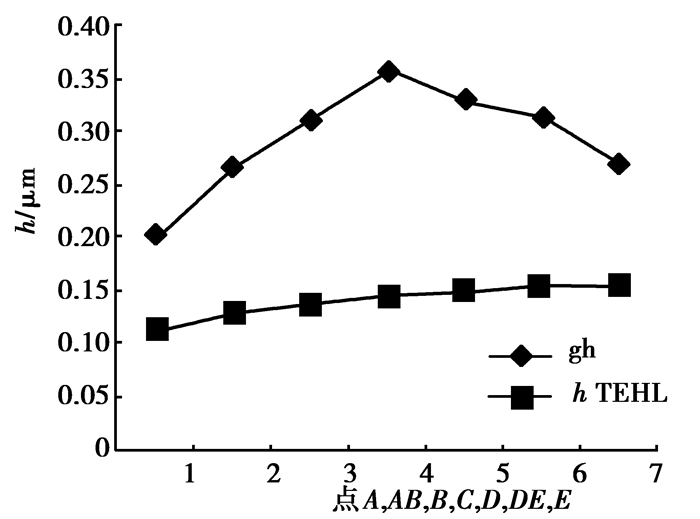
图 2 MW齿轮箱各啮合点最小油膜厚度 Figure 2 Local lubricant film thicknesses of one gear pair in a 2 MW gearbox |
|
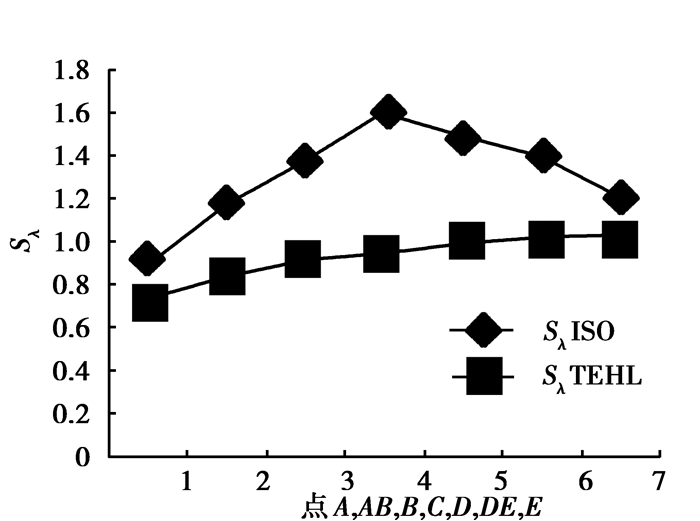
图 3 某2 MW齿轮箱各啮合点微点蚀安全系数 Figure 3 Safety factors against micro-pitting of one gear pair in a 2 MW gearbox |
|
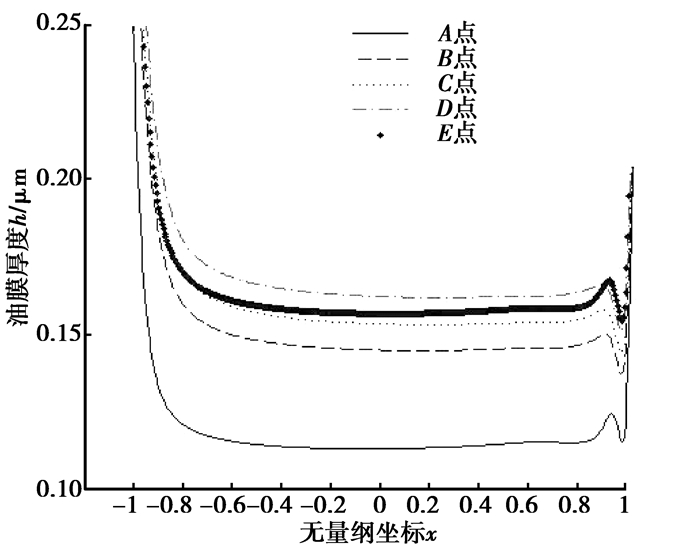
图 4 各啮合点油膜形状 Figure 4 Film shapes of main contact point |
|
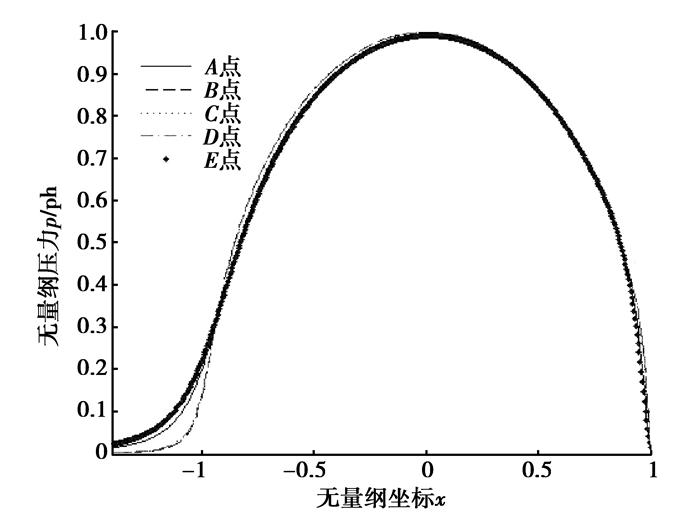
图 5 各啮合点压力分布 Figure 5 Film pressure distributions of main contact point |
|
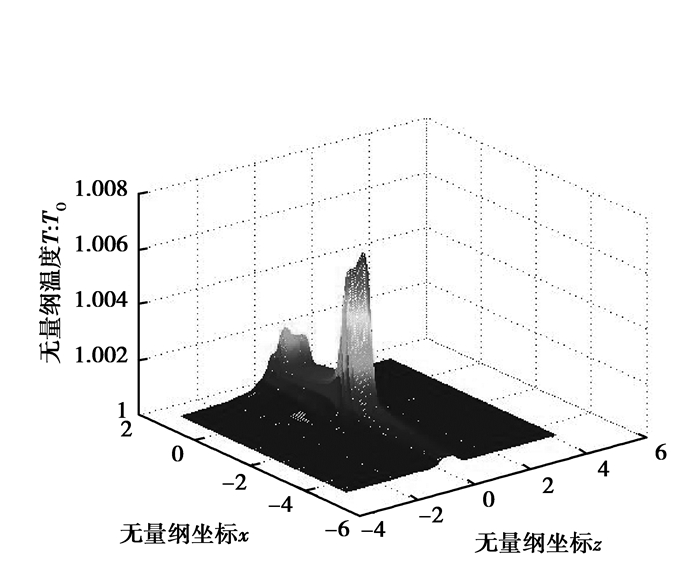
图 6 A点温度分布图(z=0,1:齿油分界面) Figure 6 Temperature distribution of contact point A (z=0 and 1 are boundaries between gear and oil) |
|
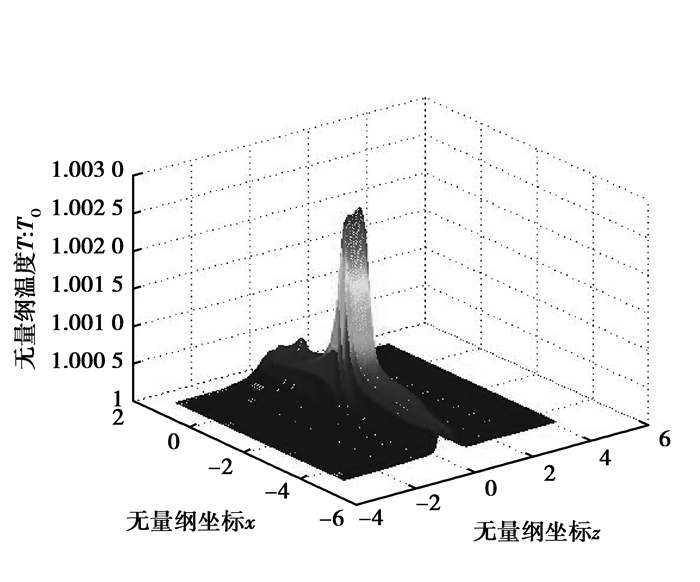
图 7 C点温度分布图(z=0,1:齿油分界面) Figure 7 Temperature distribution of contact point C (z=0 and 1 are boundaries between gear and oil) |
| Sλ=hminRa/(1.4hrefRaref), |
式中下标ref为SKS10计算出的最小油膜厚度。
由图 2、图 3可知:没有修形的风电齿轮副的最小油膜厚度为A点,但通过齿形修形可降低A点赫兹接触压力,进而增加油膜厚度;采用热弹流润滑分析得到的微点蚀安全系数低于使用ISO/TR 15144-1计算的油膜厚度;两种方法计算的各啮合点的微点蚀安全系数的差距小于最小油膜厚度的差距,这主要是由于两种不同方法计算出的href也不同。
由图 4,图 5可知:对于风电低速级齿轮副,最小油膜位于赫兹接触区出口一侧,该处存在明显的颈缩;个别啮合点存在颈缩前突然膜厚变厚现象,使颈缩处的油膜厚于中心油膜,这是由于入口区温度较高引起的;正常工作载荷下不存在第二压力峰值,而且最大接触压力基本等于赫兹接触压力(ph)。由图 6、图 7可知:与一些文献中的轴承[16]不同,最大温升位于赫兹接触区入口一侧; C点与A点的温升差异较小,这也导致C点没有出现使用ISO/TR 15144-1计算的油膜厚度大幅增加。
4 结论1)使用多重网格法的热弹流润滑理论可以用于直接计算微点蚀性能,且用该方法计算的风电齿轮箱低速级齿轮微点蚀安全系数小于用ISO/TR 15144-1的安全系数。
2)由于计算的过程及计算方法不同,使用多重网格法的热弹流润滑理论计算的最小油膜厚度低于ISO/TR 15144-1采用的Dowson/Higginson拟合的计算公式。鉴于齿轮实际啮合油膜厚度很难准确测量,两种方法的准确性尚需进一步验证,但热弹流润滑分析得到的安全系数偏低,可作为微点蚀安全系数计算的参考方法。
3)风电主齿轮箱因齿轮啮合产生油膜厚度远低于齿轮副的修形量,且因弹流润滑产生压力变化极小,因而通过齿面受载分析确定修形量时可以不考虑润滑油膜造成的接触形式及接触压力的变化。
| [1] | 李国云, 秦大同. 风力发电机齿轮箱加速疲劳试验技术分析[J]. 重庆大学学报:自然科学版, 2009, 32(11): 1252–1256. |
| [2] | Michaud M, Sroka G J, Benson R E. Refurbishing Wind Turbine Gears[J]. Gear Solutions, 2011(6): 28–39. |
| [3] | Feng Y, Qiu Y, Crabtree C J, et al. Monitoring wind turbine gearboxes[J]. Wind Energy, 2013, 16(5): 728–740. DOI:10.1002/we.v16.5 |
| [4] |
颜力, 刘忠伟.
兆瓦级风电齿轮微点蚀的研究[J]. 机车车辆工艺, 2012(6): 10–11,14.
YAN Li, LIU Zhongwei. Research on Micro pitting of gear flanks for MW Wind Turbin[J]. Locomotive & Rolling Stock Technology, 2012(6): 10–11,14. (in Chinese) |
| [5] | Netpu S, Srichandr P. Failure of a helical gear in a power plant[J]. Engineering Failure Analysis, 2013, 32: 81–90. DOI:10.1016/j.engfailanal.2013.03.002 |
| [6] | Sinha Y, Steel J A, Andrawus J A, et al. Significance of Effective Lubrication in Mitigating System Failures-A Wind Turbine Gearbox Case Study[J]. Wind Engineering, 2014, 38(4): 441–450. DOI:10.1260/0309-524X.38.4.441 |
| [7] | ISO/TR 15144-1:2010.Calculation of micropitting load capacity of cylindrical spur and helical gears-Part 1:Introduction and basic principles[S]. |
| [8] | Lloyd G. Rules and regulations, IV-industrial services, part 1-guideline for certification of wind turbines[J]. 2010. |
| [9] | Kissling U. Application of the first international calculation method for micropitting[J]. Gear technology, 2012, 29(5): 54–60. |
| [10] | Errichello R L. Morphology of Micropitting[J]. Gear Technology, 2012, 11: 74–80. |
| [11] | Moorthy V, Shaw B A. An observation on the initiation of micro-pitting damage in as-ground and coated gears during contact fatigue[J]. Wear, 2013, 297(1): 878–884. |
| [12] | Fu X X, Wang Y Q. The Elastohydrodynamic Lubrication Analysis of Composite Material Gear[J]. Advanced Materials Research, 2013, 706: 1622–1626. |
| [13] | Xue J, Li W, Qin C. The scuffing load capacity of involute spur gear systems based on dynamic loads and transient thermal elastohydrodynamic lubrication[J]. Tribology International, 2014, 79(11): 74–83. |
| [14] | 杨沛然. 流体润滑数值分析[M]. 北京: 国防工业出版社, 1998. |
| [15] |
黄平, 温诗铸.
多重网格法求解线接触弹流问题[J]. 清华大学学报:自然科学版, 1992(5): 26–34.
HUANG Ping, WEN Shizhu. Solutions of the elastohydrodynamic lubrication line contact problems with multigrid method[J]. Journal of Tsinghua University: Science and Technology, 1992(5): 26–34. (in Chinese) |
| [16] |
熊永强, 尹忠慰, 彭颖红.
轴瓦的力学性能对水润滑塑料轴承润滑性能的影响[J]. 润滑与密封, 2011, 36(2): 9–11.
XIONG Yongqiang, YIN Zhongwei, PENG Yinghong. The effects of mechanical properties of bearing bush on water lubricated plastic bearing lubricating property[J]. Lubrication Engineering, 2011, 36(2): 9–11. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38


