风电齿轮箱是风力发电机组的关键部件和传动链中可靠性相对薄弱的一个环节。风电机组通常安装在荒郊野外、服役工况极其恶劣;同时,由于受安装空间和吊装成本的限制,要求齿轮箱在保证使用寿命和可靠性的前提下,体积小、重量轻。随着机组单机容量的逐渐增大,风电齿轮箱的可靠性与轻量化设计制造之间的矛盾日渐突出,因此,与传统工业齿轮箱相比,一些新的高可靠性、高功率密度设计制造技术在风电齿轮箱、特别是增速齿轮箱的生产中得到了广泛应用[1-2]。
要提高齿轮箱的功率密度,一是通过设计制造手段充分提高齿轮传动的承载能力,二是在满足各种性能指标的前提下,最大限度地减轻零部件的重量和尺寸。因此,提高风电齿轮箱功率密度的途径主要有减小齿轮传动载荷、提高齿轮极限应力及轻量化其他零部件等。
1 减小齿轮传动载荷齿轮传动设计中主要考虑接触疲劳强度和弯曲疲劳强度。通常情况下,接触强度设计决定齿轮箱的主要几何尺寸和重量。在所有几何参数中,中心距是齿轮传动轻量化的一个最重要指标,其大小决定了产品的设计水平,对风电齿轮箱也是如此。根据接触疲劳强度计算方法[3],齿轮传动的中心距应满足式(1)条件。
| $ a \ge \left( {u \pm 1} \right) \cdot \sqrt[3]{{\frac{{250{K_{\rm{A}}}{K_{\rm{V}}}{K_{{\rm{H\alpha }}}}{K_{{\rm{H\beta }}}}{T_1}}}{{{\varphi _a}u}}}} \cdot \sqrt[3]{{{{\left( {\frac{{{Z_{{\rm{BD}}}}{Z_{\rm{H}}}{Z_{\rm{E}}}{Z_{\rm{\varepsilon }}}{Z_{\rm{\beta }}} \cdot {S_{{\rm{Hmin}}}}}}{{{Z_{\rm{L}}}{Z_{\rm{V}}}{Z_{\rm{R}}}{Z_{\rm{X}}}{Z_{{\rm{NT}}}}{Z_{\rm{W}}} \cdot {\delta _{{\rm{Hlim}}}}}}} \right)}^2}}} $ | (1) |
式中:a为中心距,其他参数的几何意义和计算方法参见文献[3]。
从式(1)可以看出,减少中心距、提高齿轮传动功率密度的主要途径有:减小计算载荷T1、提高齿轮疲劳极限应力σHlim、减小最小许用安全系数SHmin、增大齿宽系数φa(齿宽与中心距之比)及改变啮合型式(轮齿啮合从凸凸接触变为凸凹接触)等。
1.1 通过功率分流减小载荷设计时尽管装置传递的设计载荷一般是已经给定的,但可以通过功率分流等型式减少每对啮合副传递的计算载荷。常见的风电增速箱及偏航、变桨减速器均采用行星齿轮传动等功率分流方式以降低计算载荷,减小齿轮箱的尺寸,提高功率密度。随着设计制造水平的提高,目前行星轮的个数逐渐增多,可达6、7个甚至更多。采用多行星轮结构时,必须采用良好的均载方式和精密的制造装配技术。表 1为假定式(1)中其他参数不变,功率分流支数与中心距比值(分流传动中心距与无功率分流中心距的比值)关系。
| 表 1 功率分流支数与中心距比值 Table 1 Number of power dividing and central distance ratio |
可以看出,假如不考虑误差和均载的影响,采用6个行星轮的行星齿轮传动的中心距比定轴外啮合传动的中心距可减小45%,因此,在保证均载效果的前提下,提高行星齿轮传动行星轮的个数或增加功率分流支数是提高功率密度最有效的手段之一。随着设计技术和制造精度保证技术的提高,目前行星齿轮传动行星轮个数有逐渐增加的趋势。
1.2 通过均载技术提高啮合副之间载荷分配均匀性功率分流是提高齿轮传动功率密度的最有效手段,这也是目前行星齿轮传动应用日益广泛的重要原因。由于设计分析技术和制造精度保证技术的限制,使得行星轮的个数不能过多,要增加行星轮个数必须首先解决均载问题,均载方法和均载机构设计成为行星齿轮传动设计技术的关键。传统行星齿轮传动多采用太阳轮均载,随着风电机组单机容量的逐渐增大,许多新的均载方式在风电齿轮箱设计制造中得以应用,如柔性销轴、长太阳轮轴、薄壁齿圈等。柔性销轴结构除保留常规的太阳轮浮动外,还采用柔性的行星齿轮轴结构,使得行星轮得以浮动,有效提高了均载效果,为采用更多的行星轮提供了可能。同时,这种结构还采用单臂行星架,大大减小了行星架的轴向尺寸,减轻了行星架的重量。传统的太阳轮均载方法通常采用鼓形齿联接,结构简单、技术成熟,但只能在一定程度上解决太阳轮与行星轮啮合的均载问题;柔性销轴技术使行星轮浮动,可同时解决内啮合和外啮合的载荷不均问题,但柔性销轴的制造难度较大,涉及到材料性能、结构设计、制造工艺等技术难题,目前国内尚未完全掌握。
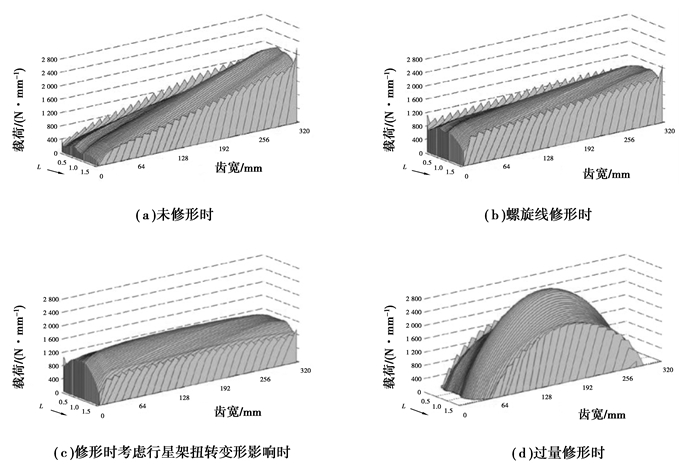
1.3 通过轮齿修形提高轮齿载荷分布均匀性齿轮轮齿的修形包括齿形修形、螺旋线修形、对角修形及三维拓扑修形等。通过修形可以达到:1)改善齿面载荷分布,提高承载能力;2)减小传递误差,降低齿轮传动噪音;3)降低摩擦损失, 提高传递效率等[4]。特别是通过修形可以明显改善载荷在齿宽方向的分布,提高齿轮的承载能力。在GB/T 3480标准所有载荷修正系数中,齿向载荷分布系数Kβ是影响因素最多、计算最复杂的。轴系结构尺寸设计不合理、制造装配误差较大时,有可能出现不合理的、较大数值的Kβ。国外有文献曾对某2 MW风电增速箱做过研究,结果表明未修形时Kβ=1.67(载荷分布见图 1(a));采用螺旋线修形时Kβ=1.23(载荷分布见图 1(b));在进一步考虑行星架扭转变形的影响时Kβ=1.16(载荷分布见图 1(c)),齿向载荷分布系数比不修形时降低了30%,中心距可降低约12%;但如果修形不当,出现过量修形时Kβ=1.98(载荷分布见图 1(d)),不但齿向载荷分布得不到改善,反而降低了承载能力[5]。齿轮轮齿的修形不能仅考虑齿轮本身的变形和误差,应对整个传动链的误差、变形等进行计算分析,这涉及到复杂的设计和制造技术,而且最终还需经试验或实际运行验证。目前国内对此缺乏深入系统的研究,难以提供适合各种工况的精确指导。
|
图 1 修形对齿向载荷分布的影响 Figure 1 The influence of tooth modification on the distribution of longitudinal load |
随着加工工艺和加工装备水平的提高,特别是数字化、智能化制造装备的大量采用,齿轮产品的制造精度也在逐步提高,这就为增大齿宽提供了装备上的保障。理论上讲,增大齿宽可明显提高承载能力,但如果制造和装配精度不能保证载荷分布的均匀性,过度增加齿宽甚至可能降低承载能力。目前,齿宽系数有逐步增大的趋势。由表 2可以看出,如果齿宽系数从0.25增大到0.4,中心距可下降15%。
| 表 2 齿宽系数与中心距比值的关系 Table 2 Face width factor and central distance ratio |
提高齿轮的接触疲劳极限应力和弯曲疲劳极限应力是提高齿轮传动功率密度和可靠性的重要手段。随着热处理工艺及其装备技术、制造精度控制技术、齿面强化技术等发展,齿轮疲劳强度极限应力必将得到较大幅度的提高。
2.1 通过齿面改性(材料和热处理方式等)提高齿轮的极限应力目前,风电齿轮箱不论是增速箱还是偏航、变桨减速器中的齿轮均采用合金钢锻件+渗碳淬火+磨齿工艺(部分内齿圈采用感应淬火热处理工艺),材料热处理质量应按ISO 6336-5(GB/T3480-5)中渗碳齿轮最高级别的ME要求来控制。由于风电齿轮箱服役条件恶劣,载荷交变、冲击频繁,齿轮轮齿常常产生微点蚀而发生早期失效,这种失效与接触精度和硬化表层物理冶金因素等有关,因此,齿轮热处理质量及其稳定性和一致性控制往往成为制约产品可靠性的关键。在美国ANSI/AGMA/AWEA6006-A03《风力发电机齿轮箱设计规范》的52项质量控制项目中,材料热处理就占20项[6];中国国家标准GB/T3480-5“齿轮强度和材料质量”中ME级质量检测项目也有14大项;国家标准GB/T 3480-1997“渐开线圆柱齿轮承载能力计算方法”中,极限应力σHlim和σFlim、使用系数KA、寿命系数ZNT和YNT等直接与齿轮材料和热处理方式有关[7]。表 3为接触疲劳极限应力与中心距比值的关系,表中以1 350 MPa为基准(大致相当于渗碳淬火ML级),700 MPa对应于调质齿轮,1 650 MPa对应渗碳淬火的ME级。可以看出ME级的中心距约比ML级可减少14%左右。最后一列的数字为假想值,如果将来出现新的热处理方法或新的齿面强化方法能将极限应力比目前提高1倍,达到2 700 MPa,则中心距可比目前ML级的降低约40%。
| 表 3 接触极限应力与中心距比值 Table 3 Contact limit stress and central distance ratio |
目前风电齿轮主要采用渗碳淬火工艺,而渗碳淬火变形是齿轮生产中的最大技术难题之一。如果热处理畸变过大,导致磨齿后层深不均甚至局部过浅,齿面硬度降低,同样会降低极限应力。齿轮热处理变形难以控制的主要原因是影响变形的因素太多,主要因素见表 4。而且,这些因素还具有以下特点:1)从技术的角度,涉及多学科;2)从生产的角度,涉及多工序;3)从管理的角度,涉及多部门;4)从措施的角度,不仅涉及技术还涉及生产成本等。国外有资料曾统计出影响热处理变形因素有26种、77个子因子。目前,渗碳淬火变形的控制主要通过以下方法进行:1)采用淬透性带宽较小的材料,提高材料的冶金质量和毛坯的锻件质量;2)合理的零件结构及机械加工工艺;3)合理的热处理工艺及精密热处理装备等。
| 表 4 影响齿轮热处理变形的主要因素 Table 4 Main factors influencing heat treatment of gears |
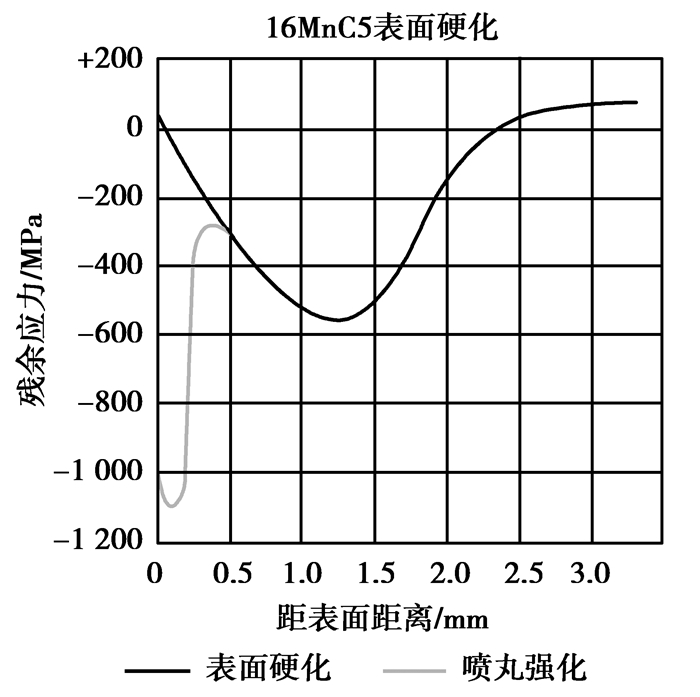
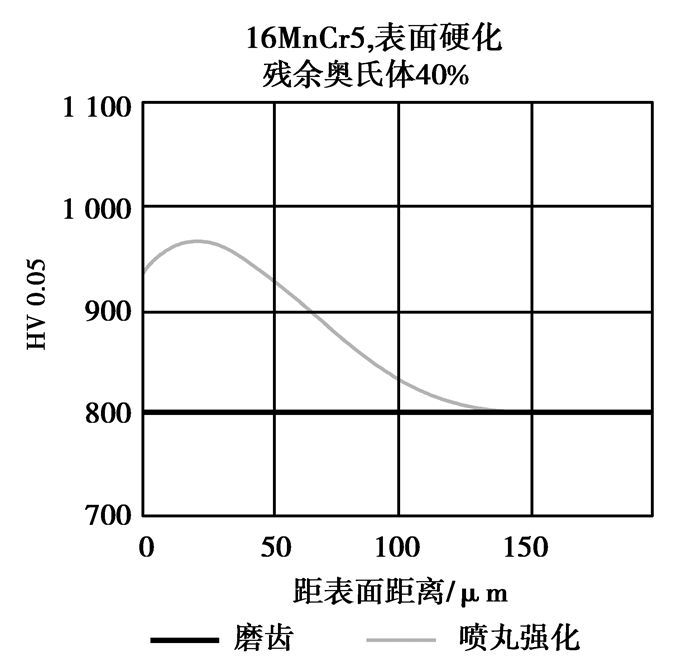
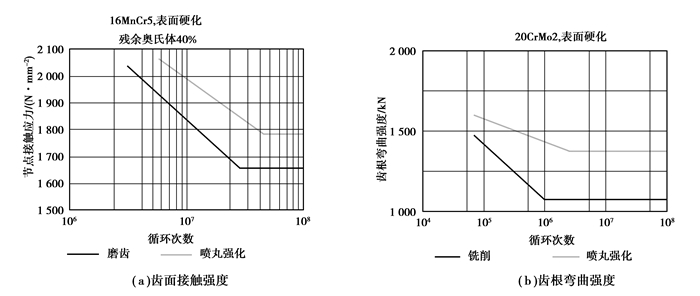
齿轮喷丸强化是一种通过无数个丸粒连续击打轮齿表面、无数凹陷重叠形成均匀残余压应力层的冷处理方法。影响喷丸强化效果的主要因素有喷丸强度、覆盖率、丸料控制及喷丸设备控制等。除增加残余压应力的数值外,喷丸强化还具有增加齿面硬度,改善轮齿次表层残余应力分布、材料组织及微观组织等功效。未经喷丸强化的渗碳淬火齿轮最大压应力一般位于表层下0.02 mm附近,最大压应力一般不超过200 MPa,经喷丸强化后,最大压应力可下移到0.05 mm处或更深,最大压应力可达600~800 MPa甚至更高[8]。图 2为喷丸强化对残余应力分布的影响,图 3为喷丸强化对齿面次表层硬度分布的影响,图 4为喷丸强化对齿面接触强度和齿根弯曲强度的影响。
|
图 2 喷丸强化对残余应力分布的影响 Figure 2 The influence of shot peening on the distribution of residual stress |
|
图 3 喷丸强化对齿面次表层硬度分布的影响 Figure 3 The influence of shot peening on the hardness distribution of tooth subsurface |
|
图 4 喷丸强化对齿面接触强度和齿根弯曲强度的影响 Figure 4 The influence of shot peening on the contact strength of tooth surface and the bending strength of tooth root |
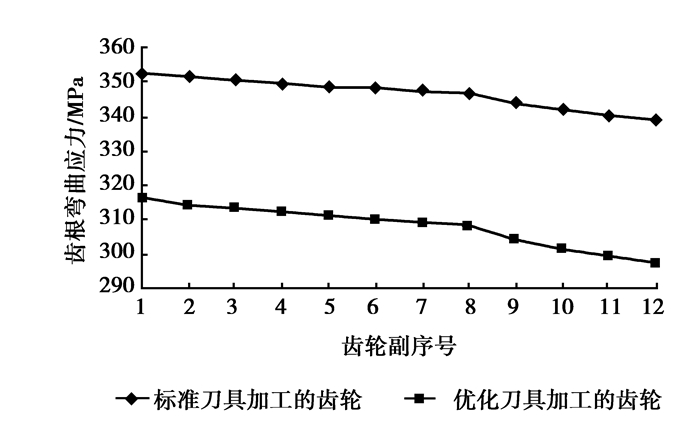
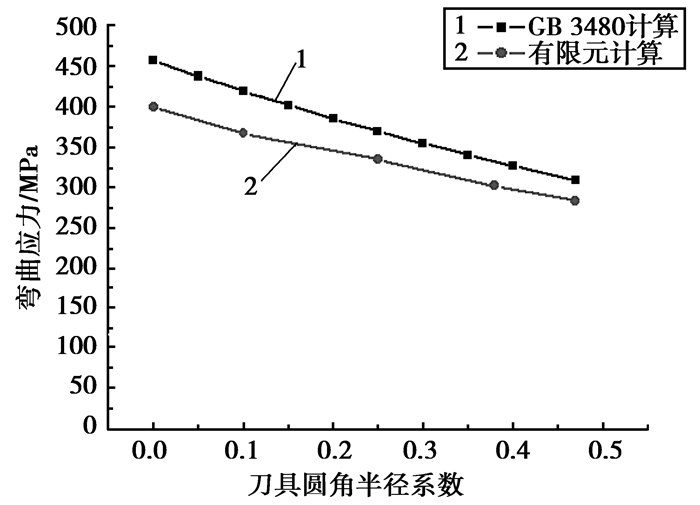
齿根过渡曲线的形状和形貌对齿根应力集中有重要影响,进而会影响齿轮弯曲疲劳极限应力的大小。由于磨齿时一般不磨削齿根,齿根形貌主要取决于制齿加工时刀具的齿顶形状和磨齿时磨削加工面与未磨削加工面连接处的形貌。如何降低齿根过渡曲线处的应力集中是提高齿轮承载能力的有效途径之一。不同形状滚刀加工的齿轮齿根的最大应力是不同的,文献[9]研究了圆角半径、齿顶高系数等刀具几何参数对所生成齿轮齿根弯曲应力的影响,通过优化滚刀几何参数,可以有效降低齿根弯曲应力,图 5为几何参数优化后的滚刀与标准滚刀对齿轮齿根最大应力的影响。在刀具几何参数中,刀具圆角半径系数对齿根弯曲应力影响较大。总体而言,增大圆角半径系数有利于提高弯曲强度,当齿轮齿数较少时(如小于14),圆角半径系数对弯曲强度的影响更大,图 6为刀具圆角半径系数与某齿数为8的齿轮齿根弯曲应力的关系。
|
图 5 滚刀形状对齿根弯曲应力的影响 Figure 5 The influence of hob shape on the bending stress of tooth root |
|
图 6 刀具圆角半径系数对齿根弯曲应力的影响 Figure 6 The influence of fillet radius coefficient on the bending stress of tooth root |
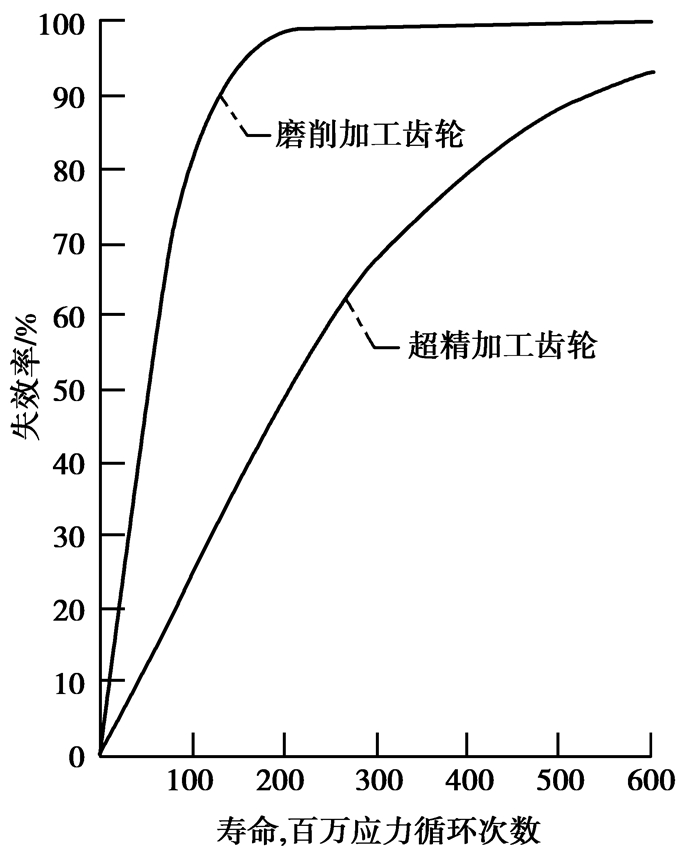
风电齿轮箱属低速重载齿轮传动,受交变冲击载荷作用,齿面微点蚀成为较常见的失效形式。正是由于微点蚀在低速重载齿轮传动中出现的普遍性和对高端传动装置运行寿命及可靠性的严重影响,国外近年来这方面的研究十分活跃,对微点蚀的各种影响因素进行了系统研究,普遍认为齿面粗糙度、润滑、齿面组织状态等因素对微点蚀有很大影响,提高齿面硬度、降低齿面摩擦系数可明显提高齿面的抗微点蚀能力[10-11]。国外已经证明对提高轮齿表面抗微点蚀能力最有效的手段是采用超精加工工艺降低轮齿表面的粗糙度,同时, 采用超精加工工艺处理过的齿轮副, 其疲劳强度也得以提高,运行温度及噪音下降,磨损也大大减少[12]。国外研究表明普通磨齿时齿面粗糙度可达Ra=0.434 μm,采用第一次超精加工后Ra=0.083 μm,第二次超精加工后可达Ra=0.056 μm。图 7为超精加工与普通磨齿工艺对可靠性的影响。
|
图 7 齿面精加工方法对可靠性的影响 Figure 7 The influence of tooth surface finishing on reliability |
最小安全系数是考虑齿轮强度计算过程中由于服役工况、制造质量、装配质量、运行维护等不确定因素的影响而引入的裕度系数。对风电增速齿轮箱,GB/T 19073-2008规定,根据GB/T 3480按真实载荷谱计算齿轮接触疲劳强度时,取SHmin=1.25;AGMA6006规定,根据AGMA2001计算齿轮抗点蚀能力时,取SHmin=1.0,根据ISO6336计算时取SHmin=1.25[13]。表 5为按式(1)计算的最小安全系数与中心距比值的关系。
| 表 5 计算最小安全系数与中心距比值的关系 Table 5 Minimum safety factor and central distance ratio |
随着制造工艺水平、制造装备自动化程度、工人操作技能及生产管理水平的提高,风电齿轮箱制造质量的稳定性和一致性必将得到逐步提升。同时,通过科学地确定设计输入条件、计算支撑数据等,设计计算中的不确定因素会逐渐降低,使计算得到的寿命或安全系数与实际运行之间的差异逐步减少,此时,设计计算时就可取较小的安全系数。
3 其他零部件轻量化技术除上述提高齿轮传动承载能力各种途径外,行星架、箱体、轴承、轴及花键联结等零件的轻量化对提高风电齿轮箱的功率密度也至关重要。
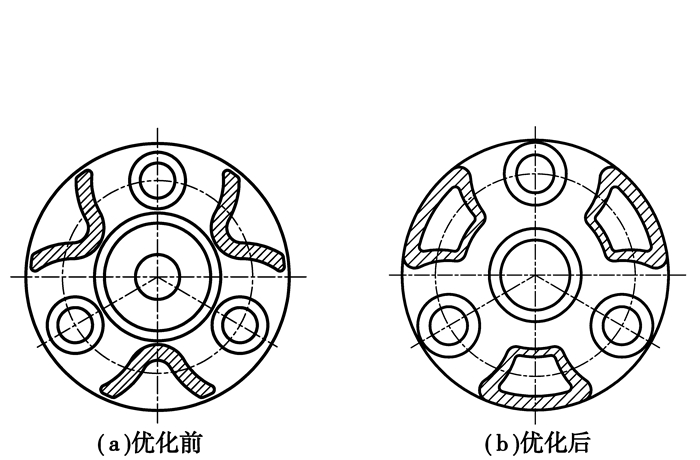
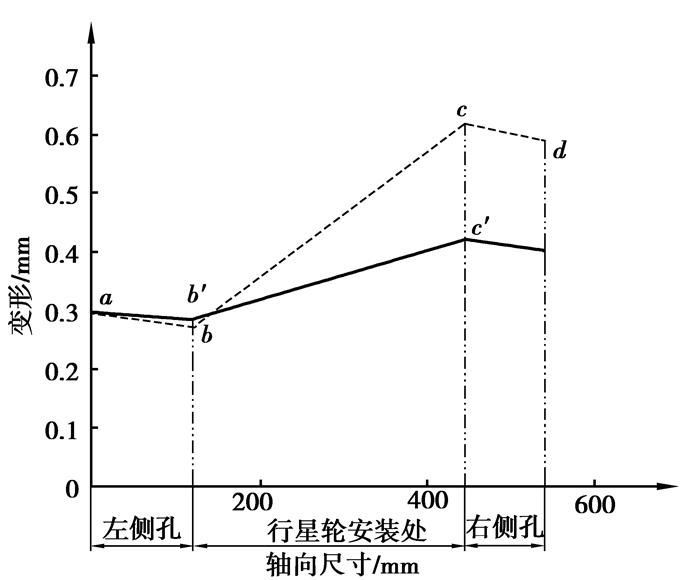
行星架是行星传动中结构较复杂的零件,承受力矩最大,重量和尺寸也较大,其变形对行星级的内、外啮合齿轮传动的质量和可靠性有很大影响,因此要求行星架要有足够的强度、刚度和较小的尺寸、重量。传统设计中,行星架主要依靠经验类比或简化模型设计,盲目性大,不但影响了设计的可靠性,更谈不上追求理想的重量和尺寸。对大型风电增速箱而言,对行星架采用结构和尺寸优化可在重量减轻的情况下明显提高行星架的整体刚度,使受载变形明显下降。如郑州机械研究所将行星架两壁之间的单板连接结构变为封闭的环状结构,环状结构的外壁厚度大于内壁厚度,两侧边为外厚内薄的渐变形状。图 8为行星架优化前后的截面图,图 9为行星架结构优化前后行星轮轴孔变形比较,图中虚线为结构优化前的变形曲线,实线为优化后的变形曲线。与同尺寸常规结构的行星架相比,行星架的最大变形下降了25%左右,重量下降10%左右,特别是行星轮轴孔处的最大变形下降了60%,有效降低了内啮合和外啮合齿轮传动的偏载,不但减轻了重量,还提高了行星传动的承载能力和可靠性[14]。
|
图 8 行星架优化前后截面图 Figure 8 Sectional views of planet carrier before and after optimization |
|
图 9 行星架结构优化前后行星轮轴孔变形比较 Figure 9 Shaft hole deformation comparison before and after planet carrier optimization |
随着风电机组单机容量的不断增大和海上风电机组装机容量的迅速扩大,不论从安装空间限制还是吊装成本考虑,风电齿轮箱的轻量化、减量化制造日趋重要。另一方面,风电齿轮箱运行环境特殊而恶劣,可靠性要求高,一旦出现故障就会造成重大经济损失。因此,轻量化技术在风电齿轮箱中的应用既十分必要又应该十分谨慎。除上述讨论的途径外,轴承的选型、轴和花键等设计也是风电齿轮箱轻量化不可缺少的环节。总之,高可靠性、高功率密度风电齿轮箱的制造需要设计、制造工艺及装备、装配、生产质量控制、安装及运行维护等诸多环节的密切配合。
| [1] | Hohn B R, Stahl K, Gwinner P. Light-weight design for planetary gear transmissions[J]. Gear Technology, 2013(9): 96–103. |
| [2] |
刘忠明.
风力发电齿轮箱技术发展趋势及若干关键问题[J]. 电器制造, 2009(9): 62–64.
LIU Zhongming. The development trend of gearboxes for wind turbines and some of its key problems[J]. Electrical Manufacturing, 2009(9): 62–64. (in Chinese) |
| [3] | 国家技术监督局. GB/T 3480-1997渐开线圆柱齿轮承载能力计算方法[S].北京:中国标准出版社, 1998. |
| [4] | Palmer D, Fish M. Evaluation of methods for calculating effects of tip relief on transmission error, noise and stress in loaded spur gears[J]. Gear Technology, 2012, 1/2: 56–67. |
| [5] | Schulze T. Design and optimization of planetary gears considering all relevant influences[J]. Gear Technology, 2013(11/12): 96–102. |
| [6] | AGMA. ANSI/AGMA/AWEA 6006-A03 Standard for design and specification of gearboxes for wind turbines[S]. [S.l.]: AGMA, 2003. |
| [7] |
刘殷.
风电齿轮箱设计计算中的材料热处理影响因素分析[J]. 机械传动, 2010, 34(6): 68–72.
LIU Yin. Analysis of material & heat-treatment influence factors in design and calculation for wind turbine gearbox[J]. Journal of Mechanical Transmission, 2010, 34(6): 68–72. (in Chinese) |
| [8] | 中国机械通用零部件工业协会齿轮分会. 2014中国齿轮工业年鉴[M]. 北京: 中国轻工业出版社, 2014: 214-223. |
| [9] | 王峰.基于齿根弯曲强度的单圆弧磨前滚刀优化研究[D].郑州:郑州机械研究所, 2013. |
| [10] | Blake G, Reynolds J. Case study involving surface durability and improved surface finish[J]. Gear Technology, 2012(8): 66–75. |
| [11] | Kissling U. Application of the first international calculation method for micropitting[J]. Gear Technology, 2012(5): 54–60. |
| [12] |
赵玉良, 徐鸿钧, 姜永涛.
风电齿轮的微点蚀研究[J]. 能源工程, 2010(4): 41–44.
ZHAO Yuliang, XU Hongjun, JIANG Yongtao. Research on micropitting of gear flanks to wind turbine[J]. Energy Engineering, 2010(4): 41–44. (in Chinese) |
| [13] |
刘忠明, 段守敏, 王长路.
风力发电齿轮箱设计制造技术的发展与展望[J]. 机械传动, 2006, 30(6): 1–6.
LIU Zhongming, DUAN Shoumin, WANG Changlu. Development and prospect of design and manufacture technology of gearboxes for wind turbines[J]. Journal of Mechanical Transmission, 2006, 30(6): 1–6. (in Chinese) |
| [14] |
张志宏, 刘忠明, 张和平, 等.
大型风电齿轮箱行星架结构分析及优化[J]. 机械传动, 2008, 25(9): 54–56.
ZHANG Zhihong, LIU Zhongming, ZHANG Heping, et al. Structural analysis and optimization on the planet frame of large scaled gearbox of wind turbine[J]. Journal of Machine Design, 2008, 25(9): 54–56. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38

