非圆齿轮是一种能够实现变速比传动的集成化传动元件,具有结构紧凑、传动精确、平稳、容易实现动平衡等优点,可以代替传统的凸轮、连杆变传动比机构,因而广泛应用于自动化机械和仪器仪表。如在流量仪表行业,常以非圆齿轮作为核心部件构成容积式流量计;在纺织机械行业,使用椭圆齿轮传动装置等来周期性的改变纬纱的密度;在印刷行业,辊桶式平板印刷机的自动送纸装置就使用了非圆齿轮;在造纸机械行业,通过非圆齿轮改变工作行程和空行程的时间比例。
非圆齿轮节曲线由一段或多段不规则函数构成[1-3],其每个齿的轮廓形状也各不相同,导致加工十分困难。传统加工方法中,粗加工主要有数控铣齿加工、数控插齿加工、数控滚齿加工和线切割加工;精加工主要采用基于插齿原理的成形砂轮展成磨削方式,使用成形砂轮逐一进行单齿展成磨削,不但效率低下,加工成本也非常高[4-5]。为此,很多生产企业一般不对非圆齿轮进行磨削加工,如纺织机械中的椭圆齿轮大都采用互相配对研磨的方式,即将一对粗加工后的非圆齿轮进行长时间对滚,以期配对的非圆齿轮能达到要求的啮合状态,存在非圆齿轮互换性差、对滚时间长等突出问题。凸节曲线非圆齿轮限于工件几何条件,只能采用基于插齿原理的成形砂轮磨削[6-8]。但凸节曲线非圆齿轮占比达70%以上,现有精加工方法所存在的缺陷,已成为限制其应用的一大瓶颈问题。
文中提出了非圆齿轮的蜗杆砂轮磨削方法,建立了蜗杆砂轮磨削非圆齿轮的相关数学模型。相比传统的基于插齿原理的成形砂轮展成磨削方法,该方法具有加工效率高、成本低且易于实现自动化控制等优点。
1 齿条刀展成凸节曲线非圆齿轮数学模型蜗杆砂轮展成加工斜齿非圆齿轮的过程,类似于一对螺旋齿轮的啮合过程,不同点在于加工非圆齿轮时,刀具与齿坯的中心距是变化的。蜗杆砂轮可看成少齿数的螺旋齿轮,故蜗杆砂轮加工凸节曲线非圆齿轮时必定满足3个条件[9-10]:刀具与齿坯的法向模数和分度圆压力角相等; 刀具和齿坯在啮合点处的法向速度相等; 蜗杆砂轮在齿坯端面上的投影相当于1个齿条,此时要求齿条的节线与齿坯的节曲线相切并做纯滚动。
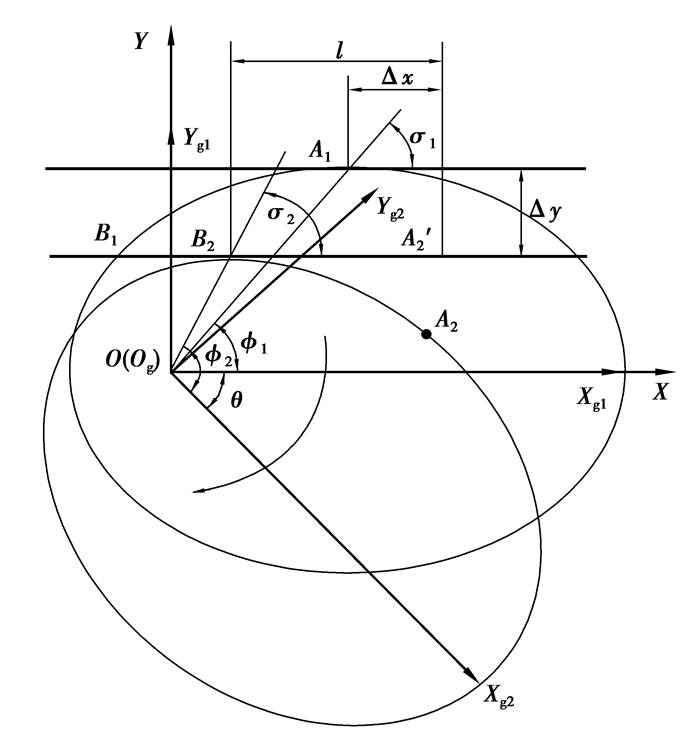
将蜗杆砂轮简化为齿条刀,建立齿条刀展成加工凸节曲线非圆齿轮数学模型。以非圆齿轮的端截面进行分析(如图 1所示),建立坐标系。设定机床坐标系S(O, X, Y)的原点与非圆齿轮的旋转中心重合,X轴平行于齿条刀具的运动方向。Sg1为齿坯初始坐标系,Sg2为齿坯顺时针旋转θ角度后的坐标系,2坐标系的X轴方向始终与齿坯的长轴重合。齿条刀具的节线始终为水平,齿坯节曲线与齿条刀节线在齿坯的2个姿态下的切点分别为A1、B2,两切点处的极角分别为φ1、φ2。齿条刀具沿其运动方向的移动距离为Δx,沿机床坐标系Y轴方向的移动距离为Δy。
|
图 1 齿条刀展成加工非圆齿轮原理图 Figure 1 The principle diagram of non-circle gear generative process by rack cutter |
根据齿轮啮合原理,非圆齿轮与齿条刀在切点处做纯滚动,滚动距离为齿轮转动极角对应的弧长l。根据图 1中的几何关系,可建立非圆齿轮蜗杆砂轮磨削数学模型。
凸节曲线非圆齿轮的节曲线方程为
| $ r = r\left( \varphi \right)。 $ | (1) |
两切触点A1、B2间的弧线长度为
| $ l = \int_{\varphi 1}^{\varphi 2} {\sqrt {{r^2} + {{\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}\varphi }}} \right)}^2}} {\rm{d}}\varphi } 。 $ | (2) |
设在工件磨削初始位置时,磨削接触点(两节线相切点)为A1,切点处的极坐标为(r1, φ1),则齿条刀的节线与齿轮极径的正向夹角为
| $ {\sigma _1} = \arctan \frac{{{r_1}}}{{\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}\varphi }}} \right)}}。 $ | (3) |
当齿轮转过θ角度后,切点B2点的极坐标为(r2, φ2),则夹角为
| $ {\sigma _2} = \arctan \frac{{{r_2}}}{{\left( {\frac{{{\rm{dr}}}}{{{\rm{d}}\varphi }}} \right)}}。 $ | (4) |
其中夹角σ的三角函数关系为
| $ \sin \sigma = \frac{r}{{\sqrt {{r^2} + {{\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}\varphi }}} \right)}^2}} }}, \cos \sigma = \frac{{\frac{{{\rm{d}}r}}{{{\rm{d}}\varphi }}}}{{\sqrt {{r^2} + {{\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}\varphi }}} \right)}^2}} }}。 $ | (5) |
齿轮两切点位置间的转角为
| $ \theta = \left( {{\varphi _2}-{\sigma _2}} \right)-\left( {{\varphi _1}-{\sigma _1}} \right)。 $ | (6) |
两切点间在x-o-y平面的位移关系分别用Δx、Δy表示
| $ \Delta x = l + {r_2}\cos {\sigma _2}-{r_1}\cos {\sigma _1}, $ | (7) |
| $ \Delta y = {r_1}\cos {\sigma _1}-{r_2}\cos {\sigma _2}。 $ | (8) |
上述公式以位移的方式给出了凸节非圆齿轮蜗杆砂轮磨削运动关系模型。
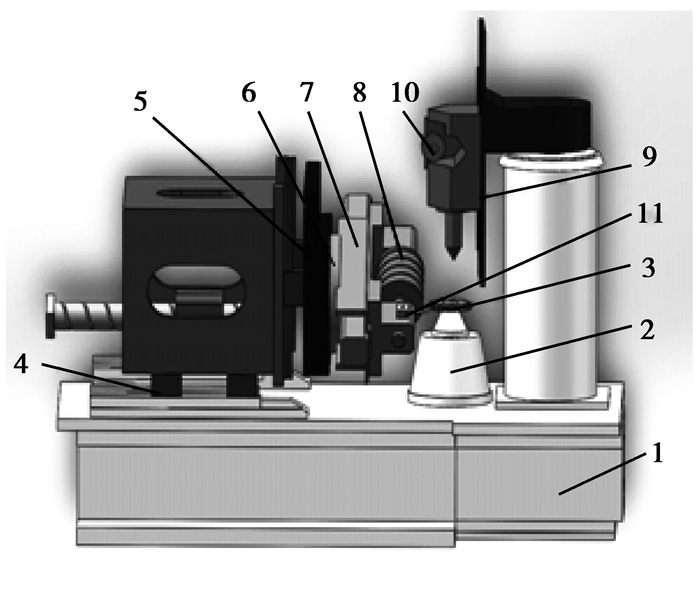
2 非圆齿轮蜗杆砂轮磨削联动模型 2.1 非圆齿轮磨削电子齿轮箱设置蜗杆砂轮磨齿机床结构如图 2所示,其磨齿原理为展成包络法。展成运动(同步轴)包括:蜗杆砂轮的径向进给运动(X轴)、蜗杆砂轮的旋转运动(B轴)、沿工件切向运动(Y轴)、沿工件轴向运动(Z轴)、工件的回转运动(C轴)。
|
图 2 蜗杆砂轮磨齿机三维结构示意图 Figure 2 The 3D structure schematic diagram of worm wheel gear grinding machine 注:1.机床床身; 2.工作台; 3.工件(齿轮); 4.X轴; 5.Z轴; 6.A轴; 7.Y轴; 8.刀具(蜗杆砂轮); 9.机床尾座; 10.金刚滚轮; 11.探测头 |
展成运动通过电子齿轮箱实现,电子齿轮箱中的运动轴称为同步轴,又分为主动轴和跟随轴,其中跟随轴只能有1个,主动轴可以为多个,主动轴为程序控制,跟随轴为跟随控制。根据需求在电子齿轮箱中建立2个联动模型,第1个联动模型中,Y、Z、B轴为主动轴,C轴为跟随轴;第2个联动模型中C轴为主动轴,X轴为跟随轴。
2.2 非圆齿轮磨削联动模型非圆齿轮的展成加工方法主要有等极角法和等弧长法[11]。等极角展成时,刀具包络线沿非圆齿轮节曲线分布不均匀,在极径越大处其包络越稀疏,在极径越小处越稠密,因此齿廓精度分布也不一致。等弧长展成刚好与等极角展成相反,其刀具包络轨迹在沿齿轮节曲线位置分布均勾,精度一致,但计算复杂[12-13]。因蜗杆砂轮磨齿机床为了保证恒定的磨削力,常采用刀具轴(B轴)恒速加工方式,故非圆齿轮蜗杆砂轮磨削采用等弧长法。
根据第1节中的磨削运动关系模型建立2个联动模型中各主动轴与跟随轴间的同步运动模型。因为蜗杆砂轮的轴线与机床坐标系的Y轴在y-o-z平面内呈一定的夹角γ,γ为加工时蜗杆砂轮的安装角,因此蜗杆砂轮的节线方向垂直于X轴方向。
1)主动轴Y、Z、B轴与跟随轴C轴
根据齿轮啮合原理,蜗杆砂轮与齿轮的啮合可作为2个斜齿轮的的啮合。蜗杆砂轮看做齿条刀时,自起始位置的相对平移速度为
| $ {v_{\rm{t}}} = \frac{{{\rm{d}}l}}{{{\rm{d}}t}}。 $ | (9) |
蜗杆砂轮沿机床坐标系Y轴方向的位移为
| $ \Delta {y_{\rm{t}}} = \Delta x = l + {r_2}\cos {\sigma _2}-{r_1}\cos {\sigma _1}。 $ | (10) |
设蜗杆砂轮沿轴向不移动,则等效的转角为
| $ {\theta _{\rm{t}}} = \frac{{\Delta {y_{\rm{t}}}}}{{{l_{{\rm{ty}}}}}} \times 360, $ | (11) |
| $ {l_{{\rm{ty}}}} = \frac{{{\rm{\pi }}{m_{\rm{n}}}{z_{\rm{t}}}}}{{\cos {\beta _{\rm{g}}}}}。 $ | (12) |
式中:lty表示蜗杆砂轮在齿轮端平面上的导程; mn、zt分别蜗杆砂轮的法面模数、头数; βg表示齿轮螺旋角。
可得蜗杆砂轮的转速为
| $ \begin{array}{l} {w_{\rm{t}}} = \frac{{{\rm{d}}{\theta _t}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{\theta _t}}}{{{\rm{d}}l}}\frac{{{\rm{d}}l}}{{dt}} = \frac{{{\rm{d}}\left[{\left( {l + {r_2}\cos {\sigma _2}-{r_1}\cos {\sigma _1}} \right)\frac{{\cos {\beta _g} \times 360}}{{{\rm{\pi }}{m_{\rm{n}}}{z_{\rm{t}}}}}} \right]}}{{{\rm{d}}l}}\frac{{{\rm{d}}l}}{{{\rm{d}}t}} = \\ \frac{{\cos {\beta _g} \times 360}}{{{\rm{\pi }}{m_{\rm{n}}}{z_{\rm{t}}}}}\left[{1 + \frac{{{\rm{d}}\left( {{r_2}\cos {\sigma _2}} \right)}}{{{\rm{d}}l}}-\frac{{{\rm{d}}\left( {{r_1}\cos {\sigma _1}} \right)}}{{{\rm{d}}l}}} \right]\frac{{{\rm{d}}l}}{{{\rm{d}}t}}。 \end{array} $ | (13) |
| $ \frac{{{\rm{d}}\left( {r\cos \sigma } \right)}}{{{\rm{d}}l}} = \left[{- r\sin \sigma \frac{{{{\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}\varphi }}} \right)}^2} + r\left( {\frac{{{{\rm{d}}^2}r}}{{{\rm{d}}\varphi }}} \right)}}{{\left[{{{\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}\varphi }}} \right)}^2} + {r^2}} \right]}} + {{\cos }^2}\sigma } \right]。 $ | (14) |
对应的非圆齿轮转速为
| $ {w_{\rm{g}}} = \frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} = \frac{{{\rm{d}}\left( {{\varphi _2}- {\sigma _2}- {\varphi _1} + {\sigma _1}} \right)}}{{{\rm{d}}l}}\frac{{{\rm{d}}l}}{{{\rm{d}}t}} = \left[{\frac{{{r^2} + 2{{\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}\varphi }}} \right)}^2} + r\left( {\frac{{{{\rm{d}}^2}r}}{{{\rm{d}}{\varphi ^2}}}} \right)}}{{{{\left[{{r^2} + {{\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}\varphi }}} \right)}^2}} \right]}^{\frac{3}{2}}}}}} \right]\frac{{{\rm{d}}l}}{{{\rm{d}}t}}。 $ | (15) |
因此B轴与C轴的同步系数为
| $ {K_{{\rm{BC}}}} = \frac{{{w_{\rm{g}}}}}{{{w_{\rm{t}}}}}。 $ | (16) |
式中,当σ=π/2且r为常数
| $ r = \frac{{2\cos {\beta _{\rm{g}}}}}{{{z_g}{m_{\rm{n}}}}}, {K_{{\rm{BC}}}} = \frac{{{z_{\rm{t}}}}}{{{z_g}}}。 $ | (17) |
此B轴与C轴的同步系数为磨削圆柱齿轮时的情况。
为了保证磨削精度,在齿轮磨削过程中,蜗杆砂轮需要沿轴向(Y向)窜刀,使未磨损砂轮区域参与磨削。
则Y轴与C轴的同步系数为
| $ {K_{{\rm{YC}}}} = \frac{{-\sin {\beta _t} \times 360}}{{{\rm{\pi }}{{\rm{z}}_{\rm{t}}}{m_{\rm{n}}}}}{K_{{\rm{BC}}}}。 $ | (18) |
式中βt表示蜗杆砂轮的螺旋角。
另外,为完成全齿宽磨削,必须要有沿Z轴方向的进给冲程。当被加工非圆齿轮为直齿轮时,Z轴方向的进给冲程不会影响齿轮的啮合关系,因此Z轴与C轴之间没有同步关系。当被加工齿轮为斜齿轮时,蜗杆砂轮沿Z轴方向进给一个工件导程时,工件旋转1周。其同步系数为
| $ {K_{ZC}} = \frac{{-\tan {\beta _g} \times 360}}{{2{\rm{\pi }}r}}。 $ | (19) |
2)主动轴C轴与跟随轴X轴
从图 1可看出,当齿轮的旋转中心固定时,非圆齿轮的极径随着极角的变化而变化,且磨齿机床上的工作台只能旋转,因此需要蜗杆砂轮沿X轴方向的移动来保证蜗杆砂轮与非圆齿轮的啮合,必须使蜗杆砂轮的径向移动轴(X)与齿轮旋转轴(C)保持同步关系。
由式(8)可得,蜗杆砂轮沿X轴方向的速度为
| $ \begin{array}{l} {v_{\rm{x}}} = \frac{{{\rm{d}}\left( {\Delta y} \right)}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\left( {\Delta y} \right)}}{{{\rm{d}}l}}\frac{{{\rm{d}}l}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\left( {{r_1}\cos {\sigma _1}- {r_2}\cos {\sigma _2}} \right)}}{{{\rm{d}}t}}\frac{{{\rm{d}}l}}{{{\rm{d}}t}} = \\ \left[{\frac{{{\rm{d}}\left( {{r_1}\cos {\sigma _1}} \right)}}{{{\rm{d}}t}}-\frac{{{\rm{d}}\left( {{r_2}\cos {\sigma _2}} \right)}}{{{\rm{d}}t}}} \right]\frac{{{\rm{d}}l}}{{{\rm{d}}t}}。 \end{array} $ | (20) |
其中
非圆齿轮的转速wg计算式(15)已给出,则C轴与X轴的同步系数为
| $ {K_{{\rm{CX}}}} = \frac{{{V_{\rm{X}}}}}{{{w_{\rm{g}}}}}。 $ | (21) |
上述所有同步关系式中,主动轴与跟随轴间是正同步还是负同步需要根据对具体机床的坐标系结构及蜗杆砂轮与齿轮的旋向分析确定。
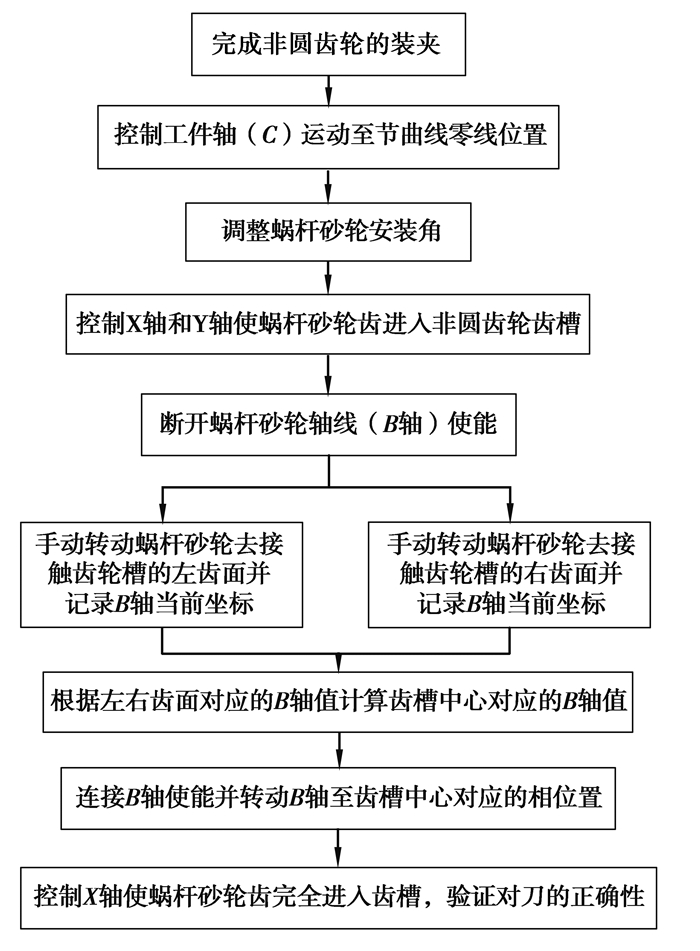
3 磨削工艺参数设置 3.1 磨削对刀非圆齿轮有对号啮合的特点,在啮合传动中要严格保证啮合齿之间的相对位置关系,因此非圆齿轮磨削时,要严格保证蜗杆砂轮与工件起始点(即零线)的相对位置,即精密对刀[14]。其对刀流程与圆柱齿轮蜗杆砂轮磨类似,如图 3所示。不同点在于,圆柱齿轮在对刀前需进行齿槽找正,即找出最优齿槽相位,而非圆齿轮因为齿槽与极角间的严格对应关系,且对刀位置固定为节曲线零线位置,故非圆齿轮对刀之前不用找正齿槽。
|
图 3 非圆齿轮与蜗杆砂轮对刀流程图 Figure 3 The flow chart of aiming by worm wheel gear and non-circle gear |
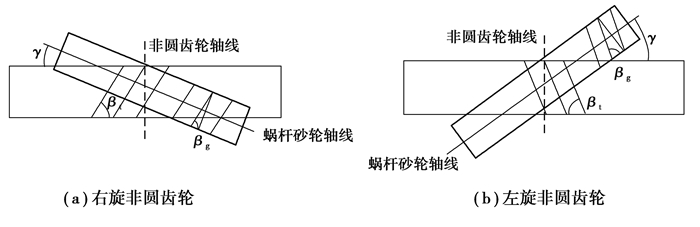
根据齿轮啮合原理,在齿轮的啮合过程中,必须保证齿轮在空间上的螺旋角相等。蜗杆砂轮和非圆齿轮由于齿向螺旋方向的不同,分为左旋、右旋和直齿。下面以右旋蜗杆砂轮为例,分析与不同旋向齿轮啮合时的安装角度(如图 4所示)。
|
图 4 蜗杆砂轮与非圆齿轮啮合时的位置关系 Figure 4 The position relation when worm wheel gear meshing with non-circle gear |
图 4中,蜗杆砂轮的螺旋线为啮合点处的螺旋线,βt表示非圆齿轮螺旋角,βg表示蜗杆砂轮螺旋角,γ表示蜗杆砂轮的安装角(规定顺时针旋转为正)。可以看出,工件右旋时,安装角为
| $ \gamma = {\beta _{\rm{g}}}-\left( {90-{\beta _{\rm{t}}}} \right)。 $ | (22) |
工件左旋时,安装角为
| $ \gamma =-\left( {90-{\beta _{\rm{t}}}} \right)-{\beta _{\rm{g}}}。 $ | (23) |
当非圆齿轮为直齿时,安装角为
| $ \gamma =-\left( {90-{\beta _{\rm{t}}}} \right)。 $ | (24) |
同理,如果蜗杆砂轮为左旋时,只需将上述公式中的(90-βt)项前的符号取为正。
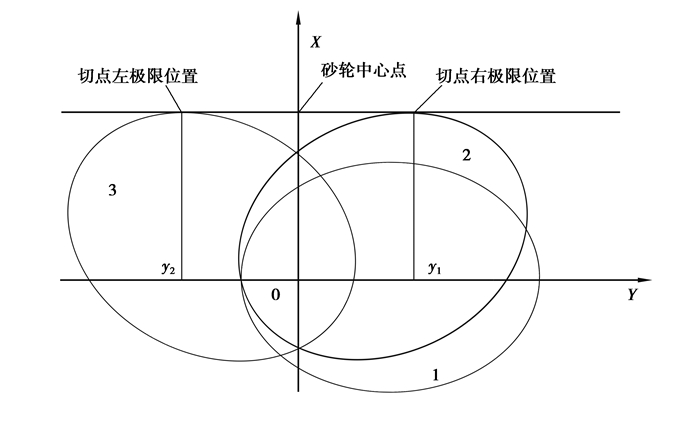
3.3 蜗杆砂轮沿自身轴向位置调整蜗杆砂轮磨削非圆齿轮时,由于非圆齿轮节曲线的不规则性,导致砂轮与齿轮的节线切点在砂轮轴线上的位置不固定(如图 1中的切点),因此必须调整蜗杆砂轮的轴向位置。将砂轮与齿轮的啮合状态投影至齿轮的端截面,砂轮的轴线平行于Y轴,以砂轮中心与齿轮旋转中心的Y轴坐标相同为例,分析磨削过程中切点在Y轴上的左右极限位置(如图 5所示)。
|
图 5 砂轮与齿轮啮合状态下在齿轮端截面的投影 Figure 5 The projection in gear end section when wheel gear meshing with gear |
图 5中,1为非圆齿轮的磨削起始位姿,2、3分别表示切点左右极限位置时的齿轮位姿。
| $ {y_1} = r\left( {{\varphi _1}} \right)\cos {\sigma _1}, $ | (25) |
| $ {y_2} = r\left( {{\varphi _2}} \right)\cos {\sigma _2}。 $ | (26) |
砂轮轴线在空间上与齿轮端截面呈一定角度,且角度为砂轮的安装角γ,设蜗杆砂轮的有效利用轴向宽度为lt,则砂轮轴向位置调整后的左右极限位置为
| $ {P_左} = \frac{{{l_{\rm{t}}}}}{2}-\frac{{{y_1}}}{{\cos \gamma }} = \frac{{{l_{\rm{t}}}}}{2}-\frac{{r\left( {{\varphi _1}} \right)\cos {\sigma _1}}}{{\cos \gamma }}, $ | (27) |
| $ {P_右} = \frac{{{l_{\rm{t}}}}}{2} + \frac{{{y_2}}}{{\cos \gamma }} = \frac{{{l_{\rm{t}}}}}{2}-\frac{{r\left( {{\varphi _2}} \right)\cos {\sigma _2}}}{{\cos \gamma }}。 $ | (28) |
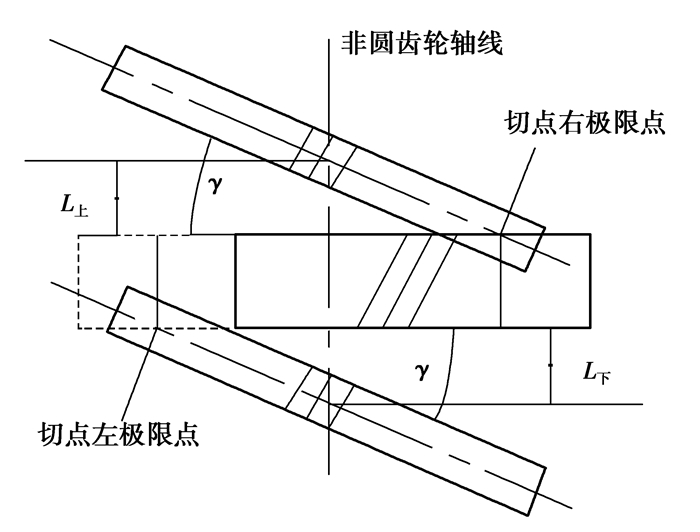
由于蜗杆砂轮与非圆齿轮的节线切点沿Y方向存在左右极限位置(如图 6所示),且蜗杆砂轮存在安装角γ。实际磨削点是沿着砂轮的安装角上下移动的,为保证齿轮上下端面圆周方向完整磨削,必须对蜗杆砂轮沿非圆齿轮轴向位置调整。
|
图 6 蜗杆砂轮沿非圆齿轮轴向位置调整 Figure 6 The axial position adjustment along non-circle gear in worm wheel gear |
当被加工齿轮为斜齿轮时,由于啮合线与齿轮端面存在一定的夹角,为保证齿轮全齿宽磨削,需要对蜗杆砂轮沿齿轮轴线的位置进行调整[15-16],设因啮合线引起的轴向调整距离分别为l上、l下。则蜗杆砂轮沿非圆齿轮轴向位置总的调整量为
| $ {L_{上}} = {y_1}\tan \gamma + {l_上}, $ | (29) |
| $ {L_{下}} = {y_2}\tan \gamma + {l_{下}}。 $ | (30) |
1)提出了一种凸节曲线非圆齿轮蜗杆砂轮磨削方法,相比传统的成形砂轮展成磨削方式,具有效率高、成本低的特点。
2)将蜗杆砂轮简化为齿条刀,以位移的方式建立了齿条刀展成加工凸节曲线非圆齿轮的运动数学模型。
3)根据现有的蜗杆砂轮磨齿机床结构及展成加工原理,对机床的电子齿轮箱进行规划,确定主动轴及跟随轴,利用等弧长加工原理推导出了机床同步轴间的同步系数,建立了展成加工联动模型。
4)给出了蜗杆砂轮与非圆齿轮的手动对刀方法及流程,并根据切点位置对蜗杆砂轮安装角、轴向位置及沿齿轮轴向位置参数进行调整。
| [1] |
刘大伟, 任廷志.
由补偿法构建封闭非圆齿轮节曲线[J]. 机械工程学报, 2011, 47(13): 147–152.
LIU Dawei, REN Tingzhi. Creating pitch curve of closed noncircular gear by compensation method[J]. Journal of Mechanical Engineering, 2011, 47(13): 147–152. (in Chinese) |
| [2] | Modler K H, Lovasz E C, Bär, G F. General method for the synthesis of geared linkages with non-circular gears[J]. Mechanism and Machine Theory, 2009, 44(4): 726–738. DOI:10.1016/j.mechmachtheory.2008.05.006 |
| [3] |
童婷, 郑方炎, 孙科, 等.
基于齿廓法线的非圆齿轮齿廓数值算法[J]. 武汉理工大学学报:交通科学与工程版, 2013, 37(3): 652–654.
TONG Ting, ZHENG Fangyan, SUN Ke, et al. Non-circular gear teeth profile numeric method based on normal tooth profile[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering, 2013, 37(3): 652–654. (in Chinese) |
| [4] |
林超, 龚海, 侯玉杰, 等.
高阶椭圆锥齿轮齿形设计与加工[J]. 中国机械工程, 2012, 23(3): 253–258.
LIN Chao, GONG Hai, Hou YUjie, et al. Tooth profile design and manufacture of higher-order elliptical bevel gears[J]. China Mechanical Engineering, 2012, 23(3): 253–258. (in Chinese) |
| [5] | Jiang Y C, Wu Z X, Tian F Y. Cutter setting calculation for cnc hobbing non-circular gear[C]// Procedings of 2011 International Conference on electric information and control Engineering, 15-17 April, 2011, Wuhan, china.Pistaway:IEEEPress, 2011:5784 -5786. |
| [6] | Song H Z, Wei S M, Liao Q Z, et al. Gearing principle of conical involute non-circular gear and simulation model[J]. Transaction of Beijing Institute of Technology, 2013, 33(8): 788–793. |
| [7] | Li J G, Zhao W, Li Z X. Noncircular gear grinding method using gear generator with form-grinding[J]. Journal of Harbin Institute of Technology, 2010, 42(11): 1749–1752. |
| [8] |
贺敬良, 李建刚, 王准, 等.
非圆齿轮的成形砂轮展成磨削原理[J]. 农业机械学报, 2007, 38(10): 145–149.
HE Jingliang, LI Jiangang, WANG Zhun, et al. Research on noncircular gear grinding method by using gear generator with form-grinding[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(10): 145–149. (in Chinese) |
| [9] |
刘永平, 杨存, 孙旋.
基于ADAMS的非圆齿轮运动学仿真分析[J]. 机械传动, 2014, 38(6): 106–109.
LIU Yongping, YANG Cun, SUN Xuan. Kinematics simulation analysis of non-circular gear based on adams[J]. Journal of Mechanical Transmission, 2014, 38(6): 106–109. (in Chinese) |
| [10] | Faydor L.Litvin, Ignacio Gonzalez-Perez, Alfonso Fuentes, Kenichi Hayasaka. Design and investigation of gear drives with non-circular gears applied for speed variation and generation of functions[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(45/48): 3783–3802. |
| [11] | Liu YY. Research on gear shaping strategy for internal helical non-circular gears and performance analyses for linkage models[J]. Journal of Mechanical Science and Technology, 2014, 28(7): 2749–2757. DOI:10.1007/s12206-014-0514-7 |
| [12] |
陈兴云, 李占贤.
非圆斜齿轮数控滚齿加工联动控制方案研究[J]. 工业技术与职业教育, 2014, 12(1): 12–17.
CHEN Xingyun, LI Zhanxian. Research on non-circular helical gear nc hobbing linkage control scheme[J]. Industrial Technology & Vocational Education , 2014, 12(1): 12–17. (in Chinese) |
| [13] | Tsay M F, Fong Z H. Study on the generalized mathematical model of noncircular gears[J]. Mathematical and Computer Modelling, 2005, 41(4/5): 555–569. |
| [14] | Lian X, Liu Y Y, Li D Z, et al. Linkage model and applications of hobbing non-circular helical gears with axial shift of hob[J]. Mechanism and Machine Theory, 2013, 70: 32–44. DOI:10.1016/j.mechmachtheory.2013.07.002 |
| [15] |
田芳勇, 胡赤兵, 姜衍仓.
非圆齿轮滚齿加工的一种自动对刀方法[J]. 兰州理工大学学报, 2010, 36(4): 41–43.
TIAN Fangyong, HU Chibing, JIANG Yancang. New method of automatic tool adjustment for non-circular gear hobbing[J]. Journal of Lanzhou University of Technology, 2010, 36(4): 41–43. (in Chinese) |
| [16] | Li W L, Wei L, Hu H Y, et al. Analysis on characteristics of minor cycle errors in process of grinding involute gears on worm wheel gear grinding machine[J]. Advanced Materials Research, 2013, 706-708: 1209–1212. DOI:10.4028/www.scientific.net/AMR.706-708 |
| [17] |
冯守卫, 张申林, 张涛, 等.
齿轮接触线长度和重合度系数[J]. 长安大学学报:自然科学版, 2004, 24(2): 101–103.
FENG Shouwei, ZHANG Shenlin, ZHANG Tao, et al. Contact line length and contact ratio coefficient of cylindrical gears[J]. Journal of Chang’an University:Natural Science Edition, 2004, 24(2): 101–103. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38


