2. 河北省万全县丰华有色金属加工厂,河北 张家口 075000
2. Hebei Wanquan Fenghua Nonferrous Manufactory, Zhangjiakou, Hebei 075000, P.R.China
随着高炉冶炼强度的提高,高炉炉腹、炉腰及炉身下部区域热负荷及温度频繁波动,工作环境恶化,冷却设备容易破损,延长此区域炉体冷却设备寿命是维持高炉长寿的关键。国内外大部分高炉在此区域安装了传热性能及抗热震性能优良的铜冷却壁[1-2]。然而,国内部分高炉铜冷却壁运行3~5年后就出现水管断裂漏水问题[3-4],并没有达到铜冷却壁设计中15~20年的长寿要求。铜冷却壁水管一旦发生断裂,在高炉现场条件下难以对其进行修复,只能停炉更换新冷却壁,严重降低高炉生产效率。
铜冷却壁水管的断裂是由于其热面高热阻渣皮脱落和黏附的反复变化过程中,铜冷却壁冷热面温差反复变化,引起其本体发生反复变形,进而导致水管根部产生疲劳应力破损[5]。然而,铜冷却壁水管的断裂也与其受到的约束作用有关。铜冷却壁水管安装设计中,为了避免水管受到炉壳的约束,在水管与炉壳开孔之间预留一定的间隙[6]。而实际上,由于安装误差等因素的影响,铜冷却壁水管与炉壳开孔的间隙距离未达到设计要求,甚至铜冷却壁安装完成后,水管与炉壳开孔直接接触,导致水管随本体变形时受到炉壳的约束作用而产生严重的应力集中。同时,相邻铜冷却壁水管之间需采用外置连接管连接,构成循环冷却水通路。外置连接管一般采用柔性水管,也有部分企业选用硬质水管,即刚性连接。刚性连接时,相当于水管末端受到固定约束作用,这也会增大铜冷却壁水管的应力集中程度。
高炉现场条件下,工作环境复杂,无法直接测量铜冷却壁水管的热应力分布,而利用数值模拟方法可以较准确地计算高炉上铜冷却壁的热应力分布,并预测不同因素对铜冷却壁热应力分布的影响[7]。吴桐等[8]通过建立铜冷却壁传热数学模型研究了高炉内铜冷却壁的适宜安装位置;魏渊等[9]研究了高炉炉腹区域铜冷却壁的温度分布;李洋龙等[10]建立了三维铜冷却壁传热数学模型,分析了铜冷却壁部分水管断水条件下的温度分布;刘增勋等[11]利用铜冷却壁传热模型研究了铜冷却壁渣皮脱落后其内部温度变化。以上研究主要集中于铜冷却壁传热分析,未考虑铜冷却壁的热变形行为。石琳等[12]采用数值模拟方法研究了高炉内铜冷却壁热应力分布及热变形行为;Shi等[13]计算了高炉炉内煤气温度对铜冷却壁热应力及热变形行为的影响。但有关铜冷却壁热应力计算模型中并未考虑水管的变形及本体变形对水管热应力分布的影响。鉴于此,笔者建立了铜冷却壁热应力分布数学模型,研究了水管所受约束和铜冷却壁变形对其热应力分布的影响,为铜冷却壁设计及安装提供参考依据。
1 物理模型高炉内铜冷却壁以螺栓及定位销固定于炉壳,水管与炉壳开孔之间一般预留8 mm左右的间隙,且水管与炉壳开孔之间以波纹补偿器进行连接,保证炉体密封性,避免炉内煤气泄漏,并弱化炉壳对水管的约束作用。铜冷却壁安装时,为了避免灌浆泥料进入波纹管与水管之间的自由空间,在水管根部增加一个套管,套管与炉壳之间由氯丁橡胶垫圈密封。相邻铜冷却壁水管之间采用柔性水管连接。在此安装方式下,水管将不受外界约束,可以随本体热变形而发生自由位移。根据铜冷却壁水管的安装方式,建立铜冷却壁物理模型,并进行如下简化和假设:
1) 忽略水管与炉壳之间的波纹管,水管套管,套管与炉壳之间的氯丁橡胶垫圈。
2) 铜冷却壁热面渣皮脱落后,本体热面与冷面温度差逐渐增加,本体受热变形程度增大,当温度分布处于稳态时达到最大变形量。鉴于此,计算中仅考虑铜冷却壁热面无渣皮覆盖稳定传热过程。
3) 为建立相邻铜冷却壁水管之间的外置连接管,将外置连接管简化成约束条件施加在水管末端。
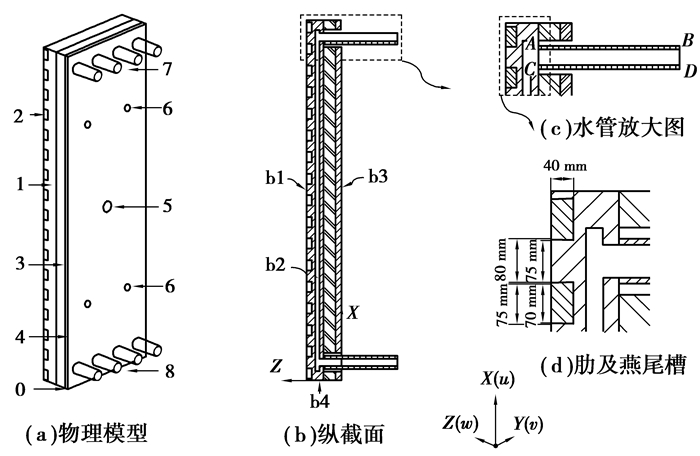
铜冷却壁物理模型如图 1所示。物理模型中包括炉壳、填料层及铜冷却壁。模型整体尺寸为2 500 mm×788 mm×230 mm,其中炉壳厚度为30 mm,填料层厚度为80 mm,铜冷却壁厚度为120 mm。铜冷却壁肋上宽为80 mm,下宽为70 mm,高为40 mm,燕尾槽上宽为70 mm,下宽为75 mm,燕尾槽内捣打耐火浇注料,如图 1(d)所示。水管内径为60 mm,外径为80 mm,长度为300 mm。铜冷却壁冷面包括一个中心定位销,并对称分布4个固定螺栓。
|
图 1 铜冷却壁物理模型 Figure 1 Physical model of copper stave 0-坐标原点;1-铜冷却壁;2-耐火浇注料;3-填料层;4-炉壳;5-定位销;6-固定螺栓;7-出水管;8-进水管;X-高度方向;Y-宽度方向;Z-厚度方向 |
铜冷却壁热应力计算是由传热计算和应力计算两部分耦合而成。首先需计算铜冷却壁内部温度分布,再将此温度分布结果作为应力计算中的载荷条件,进而得到铜冷却壁热应力分布。铜冷却壁温度分布是通过求解传热控制微分方程得到,应力分布是通过求解物理方程、平衡微分方程和几何方程3个基本微分方程得到。控制微分方程如下。
1) 传热控制微分方程。
铜冷却壁内部传热为无内热源的三维稳态导热,控制方程为:
| $ \frac{\partial }{{\partial x}}\left( {\lambda \left( T \right)\frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\lambda \left( T \right)\frac{{\partial T}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\lambda \left( T \right)\frac{{\partial T}}{{\partial z}}} \right) = 0。 $ | (1) |
2) 物理方程--热应力分量与热应变分量关系。
| $ \left\{ {\begin{array}{*{20}{c}} {{\varepsilon _x} = \frac{1}{E}\left[{{\sigma _x}-\mu \left( {{\sigma _y} + {\sigma _z}} \right)} \right] + \alpha \left( {T - {T_0}} \right), }\\ {{\varepsilon _y} = \frac{1}{E}\left[{{\sigma _y}-\mu \left( {{\sigma _x} + {\sigma _z}} \right)} \right] + \alpha \left( {T - {T_0}} \right), }\\ {{\varepsilon _z} = \frac{1}{E}\left[{{\sigma _z}-\mu \left( {{\sigma _x} + {\sigma _y}} \right)} \right] + \alpha \left( {T -{T_0}} \right), }\\ {{\gamma _{xy}} = \frac{1}{G}{\tau _{xy}}, {\gamma _{yz}} = \frac{1}{G}{\tau _{yz}}, {\gamma _{zx}} = \frac{1}{G}{\tau _{zx}}, G = \frac{E}{{2\;\left( {1 + \mu } \right)}}。} \end{array}} \right. $ | (2) |
3) 平衡微分方程--热应力分量与外力分量关系。
| $ \left\{ {\begin{array}{*{20}{c}} {\frac{{\partial {\sigma _x}}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}} = 0, }\\ {\frac{{\partial {\sigma _{xy}}}}{{\partial x}} + \frac{{\partial {\tau _y}}}{{\partial y}} + \frac{{\partial {\tau _{zy}}}}{{\partial z}} = 0, }\\ {\frac{{\partial {\sigma _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\tau _z}}}{{\partial z}} = 0。} \end{array}} \right. $ | (3) |
4) 几何方程--热应变分量与位移分量关系。
| $ \left\{ {\begin{array}{*{20}{c}} {{\varepsilon _x} = \frac{{\partial u}}{{\partial x}}, {\varepsilon _y} = \frac{{\partial v}}{{\partial y}}, {\varepsilon _z} = \frac{{\partial w}}{{\partial z}}, }\\ {{\gamma _{xy}} = \frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}, {\gamma _{yz}} = \frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}, , {\gamma _{zx}} = \frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}。} \end{array}} \right. $ | (4) |
式中:λ(T)为导热系数,W/(m·℃);T为本体温度,℃;T0为初始温度,℃;σi(i=x,y,z)为x,y,z方向上的热应力,MPa;εi为x,y,z方向上的热应变;τxy,τyz,τzx为切应力,MPa;γxy,γyz,γzx为切应变;u,v,w为x,y,z方向的位移,m (如图 1所示);G为剪切弹性模量,MPa;μ为泊松比;α为材料的热膨胀系数,℃-1。
2.2 边界条件1) 传热边界条件。
a.高温煤气与铜冷却壁热面边界b1(如图 1(b)所示)为对流和辐射的综合换热过程,即
| $ \lambda \left( T \right)\frac{{\partial T}}{{\partial N}}\left| {_{b1}} \right. = {\alpha _{\rm{f}}}\left( {{T_{\rm{f}}}-T} \right), $ | (5) |
式中:αf为高温煤气与铜冷却壁热面的综合换热系数,W/(m2·℃);Tf为热面煤气温度,℃;∂T/∂N为边界面法向温度梯度,℃/m。
b.冷却水与管内壁边界b2(如图 1(b)所示)为对流换热,即
| $ \lambda \left( T \right)\frac{{\partial T}}{{\partial N}}\left| {_{b2}} \right. = {\alpha _{\rm{w}}}\left( {T-{{\overline T }_{\rm{w}}}} \right), $ | (6) |
式中:Tw为冷却水平均温度,℃;αw为冷却水与管内壁的对流换热系数,W/(m2·℃);对流换热系数αw与冷却水速v、冷却水物性参数、管道截面形状等有关,由于管内温度分布不均匀,进水温度低于出水温度,取进出水温度的算术平均值作为定性温度,确定冷却水物性参数;冷却水道截面为半圆与矩形组成的复合型水道,属于非圆形管道,取管道的当量直径de作为定型尺寸。由管内强制对流给热方程计算,即
| $ R\;{e_{\rm{f}}} = \frac{{\rho v{d_{\rm{e}}}}}{\mu }, $ | (7) |
| $ N{u_{^{\rm{f}}}} = 0.023R\;e_{\rm{f}}^{0.8}P\;r_{\rm{f}}^{0.4}, $ | (8) |
| $ {\alpha _{\rm{w}}} = \frac{{{\lambda _{\rm{w}}}}}{{{d_{\rm{e}}}}}N{u_{^{\rm{f}}}}, $ | (9) |
式中:Ref为雷诺数;μ为冷却水的粘度,m2/s;ρ为水的密度,kg/m3;Nuf为努塞尔特准数;Prf为普朗特数;λw为冷却水的导热系数,W/(m·℃)。
c.周围环境与炉壳外表面边界b3(如图 1(b)所示)为自然对流和辐射的综合换热过程,即
| $ \lambda \left( T \right)\frac{{\partial T}}{{\partial N}}\left| {_{b3}} \right. = {\alpha _{\rm{a}}}\left( {T-{T_{\rm{a}}}} \right), $ | (10) |
式中:Ta为环境温度,℃;αa为炉壳与周围环境之间的综合换热系数,W/(m2·℃),其值由经验公式(11)[14]计算,即
| $ {a_a} = 9.3 + 0.058{T_{\rm{s}}}, $ | (11) |
式中Ts为炉壳温度,℃。
d.其他面b4(如图 1(b)所示)为绝热边界条件,即
| $ \frac{{\partial T}}{{\partial N}}\left| {_{b4}} \right. = 0。 $ | (12) |
2) 结构边界条件。
铜冷却壁安装时,在相邻两块铜冷却壁之间预留25.4~38.1 mm的膨胀间隙[5],间隙内捣打无定形耐火材料,吸收铜冷却壁受热膨胀时发生的位移。假设铜冷却壁顶底面和侧面受到10 MPa的压力, 计算中忽略炉壳沿高炉高度、周向及径向的位移,认为炉壳沿X,Y,Z向的位移为零。除以上边界受到约束以外,其他边界为自由。
2.3 物性参数铜冷却壁热应力分布计算涉及到的物性参数主要包括材料的导热系数、杨氏模量、热膨胀系数和泊松比等,不同材料的物性参数[7, 15]如表 1和表 2所示。
| 表 1 材料的导热系数 Table 1 Thermal conductivity of material |
| 表 2 材料力学性能参数 Table 2 Mechanical property parameters of materials |
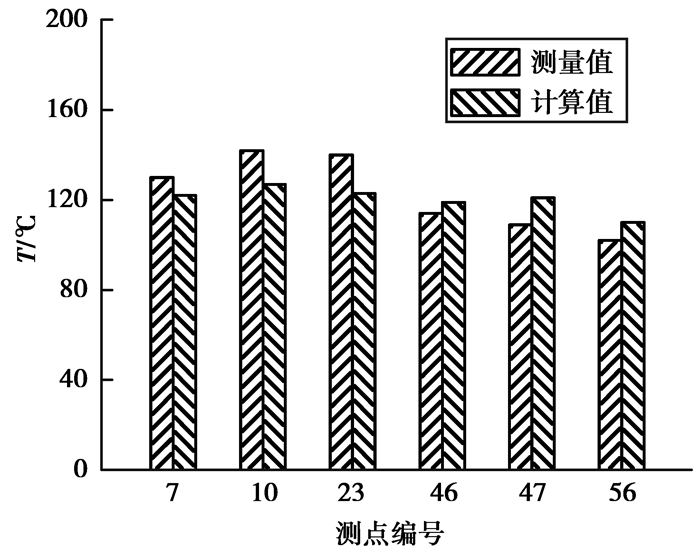
为了验证数学模型的准确性,根据石琳等[7]热态试验中铜冷却壁的传热条件,应用本数学模型计算了此条件下铜冷却壁的温度分布,并与其热态试验测量值进行对比分析。图 2为热态试验条件下铜冷却壁温度计算值与测量值。从图中可以看出,对于同一测点位置,铜冷却壁计算值与测量值的相对误差约为4.3%~12.1%,接近相等。可见,本数学模型可以准确计算铜冷却壁温度分布,间接证明本数学模型也可以准确计算铜冷却壁水管的热应力分布。
|
图 2 铜冷却壁温度计算值与测量值对比 Figure 2 Comparison of calculated and measured temperature in copper stave |
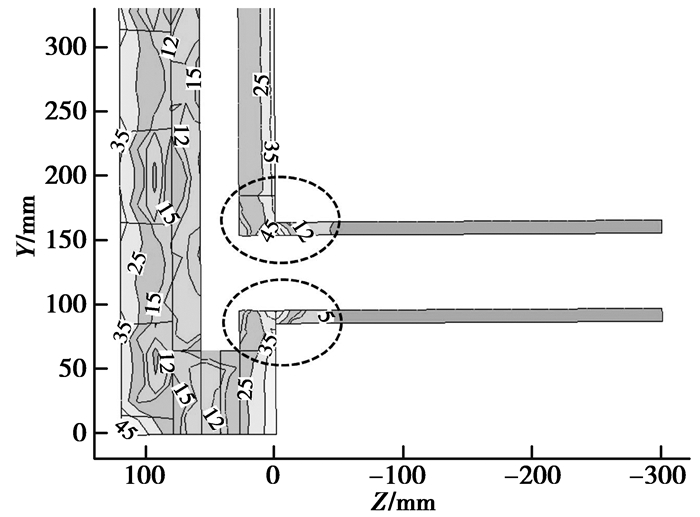
图 3为铜冷却壁水管不受约束时的等效应力分布。图中仅给出图 1(c)所示位置水管等效应力分布。从图中可以看出,铜冷却壁热面及冷面等效应力大于35 MPa,底端角部位置大于45 MPa,其内部等效应力接近12 MPa,铜冷却壁内部热应力由表面至内部逐渐减小。铜冷却壁水管根部位置等效应力约为45 MPa,大于铜冷却壁内部热应力,说明水管不受约束时其根部也会产生较大热应力。但水管自由时其根部最大等效应力低于纯铜的屈服强度62 MPa[16],不易发生屈服失效损坏。
|
图 3 铜冷却壁水管不受约束时的等效应力分布 Figure 3 Equivalent stress distribution of copper stave for water pipe is free |
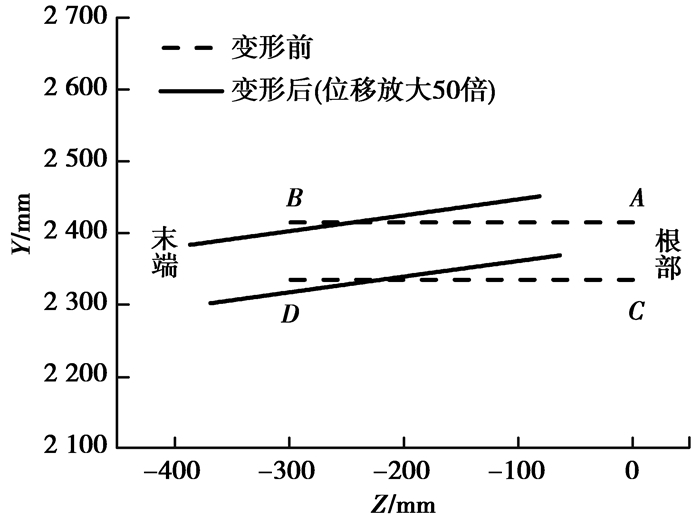
图 4为铜冷却壁水管末端自由时水管变形前后对比。从图 4(a)可以看出,当水管末端自由时,线AB和CD变形前后间距未变,长度未发生变化,仅发生了转动,说明水管未发生变形。由于水管末端自由,不受约束,水管将随本体变形而发生自由转动,不产生变形。因此,水管上热应力较小。
|
图 4 铜冷却壁水管末端自由时其变形前后对比 Figure 4 Deformed and undeformed shape of water pipe of copper stave for the terminal of water pipe is free |
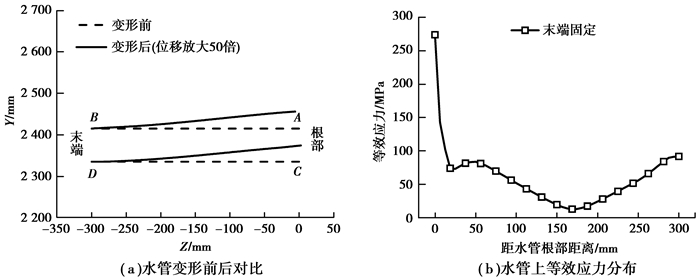
图 5为水管末端固定时水管变形及等效应力分布,其中位移放大50倍。由图 5(a)可见,当水管末端受固定约束时,水管根部沿本体长度方向发生位移,说明水管发生弯曲变形。水管上等效应力分布如图 5(b)所示。由图可知,水管末端受到固定约束时,水管上的最大等效应力为272 MPa,位于水管根部,随着距水管根部距离增加,水管等效应力先降低后升高。对比水管末端受固定约束与自由时最大等效应力(图 3)可知,水管末端自由时最大等效应力远低于其末端受固定约束时的最大等效应力。水管不受约束时,铜冷却壁热面温度高,冷面温度低,热面伸长量大于冷面,将产生弯曲变形,本体中心向炉内弯曲,导致水管随本体弯曲变形而发生自由转动。若水管末端受到固定约束,末端不发生位移,水管根部将随本体变形而沿高度方向(X方向)发生位移,在水管与本体连接界面上产生较大的热应力。因此,水管末端受固定约束时,即水管之间采用刚性连接,水管与本体焊接位置容易发生开裂漏水问题,建议水管之间选用柔性水管连接。
|
图 5 水管末端受固定约束时变形及热应力分布 Figure 5 Deformation and thermal stress distribution of water pipe for the terminal of water pipe is fixed |
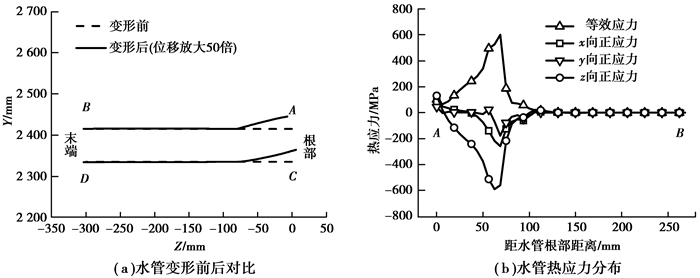
图 6为炉壳开孔约束对水管变形及热应力分布的影响。从图 6(a)中可以看出,水管根部沿本体高度方向发生位移,炉壳开孔与末端之间未发生位移,说明水管发生弯折变形,变形后呈“曲棍”形,折点位于炉壳开孔附近。由图 6(b)可知,在水管根部位置等效应力为101 MPa,随着距水管根部距离增加,水管等效应力逐渐升高,当距水管根部距离为68 mm时,即炉壳开孔位置,水管达到最大等效应力600 MPa;距水管根部距离由68 mm至80 mm时,水管等效应力逐渐减小;距水管根部距离大于80 mm时,等效应力几乎为零。从线上各点沿X,Y,Z向的正应力分布可知,水管与炉壳开孔接触位置沿X,Y,Z向正应力小于零,表现为受压状态。水管不受约束时,铜冷却壁沿高度方向(X向)及宽度方向(Y向)发生伸长变形,沿Z向发生弯曲变形,水管将随铜冷却壁沿X,Y,Z向发生位移,但在炉壳开孔约束作用下,水管与炉壳开孔接触位置无法沿X,Y,Z向自由移动,而水管根部需随本体变形而发生相应位移,导致水管发生弯折变形。所以,水管与炉壳开孔接触时,在接触位置沿X,Y,Z向表现为受压状态。由以上分析可知,当水管受到炉壳开孔约束时,水管与炉壳开孔接触位置容易发生热应力破损。
|
图 6 炉壳约束对水管变形及热应力分布影响 Figure 6 The influence of constraint of the shell on the deformation and thermal stress distribution of water pipe |
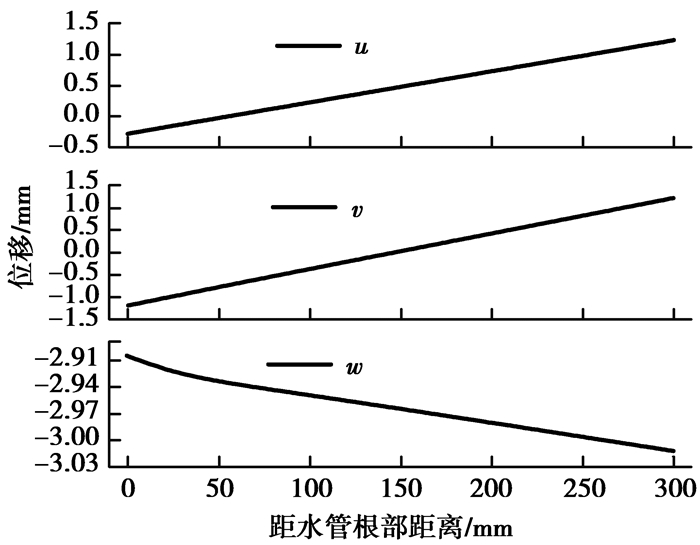
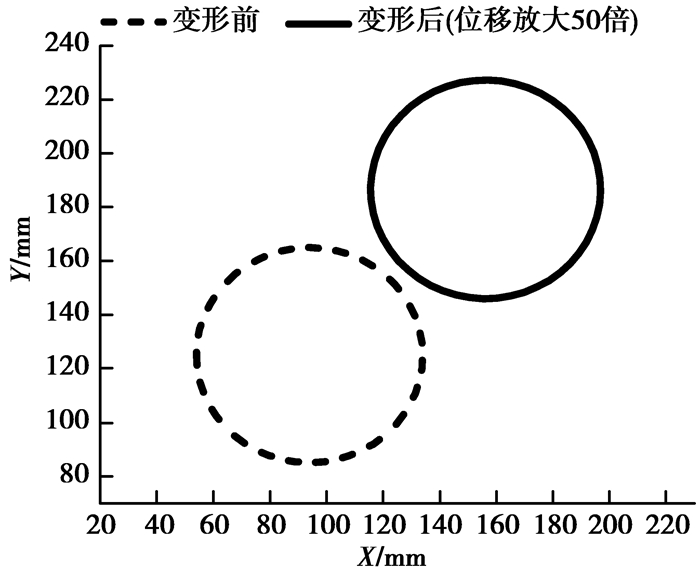
炉壳开孔直径设计中,不仅应考虑到安装误差的影响,也应考虑到水管变形产生的位移的影响。为了确保水管不受炉壳开孔约束,将铜冷却壁处于极限工作温度下水管的最大位移作为临界位移。只要炉壳开孔直径与铜冷却壁安装误差和水管外径的差值小于临界位移,说明水管将不受炉壳开孔约束。图 7为铜冷却壁极限工作温度(250 ℃)下水管(不受约束)位移分布,图中给出线AB上各点沿X(高度方向),Y(宽度方向),Z(厚度方向)向的位移u,v,w分布。从图中可以看出,水管X向位移u由-0.27 mm变化至1.23 mm,说明水管根部沿X负向产生位移,水管末端沿X正向产生位移,且在水管中部某点X向位移为零;水管沿Y向位移v由-1.18 mm变化至1.22 mm,说明水管根部沿Y负向产生位移,水管末端沿Y正向产生位移,在水管中部某点Y向位移为零;水管沿Z向位移w由-2.91 mm变化至-3.01 mm,说明水管沿Z负向产生位移。水管末端截面变形前后对比如图 8所示。从图中可以看出,水管末端截面未发生变形,仅发生移动,其移动方向沿X,Y正向。由图 7可知,水管末端沿X,Y向位移分别约为1.23 mm和1.22 mm,它们的合位移为1.73 mm。因此,临界位移为1.73 mm。
|
图 7 铜冷却壁极限工作温度下水管位移分布 Figure 7 The displacement distribution of water pipe under the critical work temperature of copper stave |
|
图 8 铜冷却壁极限工作温度下水管末端截面变形前后对比 Figure 8 Deformed and undeformed shape of cross-section of water pipe under the critical work temperature of copper stave |
铜冷却壁水管炉壳开孔尺寸设计中,炉壳开孔尺寸是水管尺寸的1.44倍[6]。按本文铜冷却壁水管直径为80 mm计算,炉壳开孔直径为115.20 mm,那么炉壳开孔与水管之间的间隙尺寸为17.10 mm。考虑到临界位移的影响,应设炉壳开孔与水管直径之间的间隙尺寸为18.83 mm,即炉壳开孔直径为117.66 mm。再加上炉壳变形等其他因素的影响,炉壳开孔直径应为120 mm。
5 结论1) 建立了铜冷却壁水管热应力分布数学模型,应用此数学模型计算了前人热态试验条件下铜冷却壁的温度分布,计算结果与测量结果基本吻合,数学模型可以用于研究高炉内铜冷却壁水管的热应力分布。
2) 铜冷却壁水管末端不受约束或受到固定约束时,其根部热应力大于其他位置热应力。但水管末端不受约束时,其最大等效应力仅为45 MPa,低于纯铜的屈服强度;水管末端受固定约束时,其最大等效应力达到272 MPa,超过纯铜的屈服强度。因此,铜冷却壁水管末端应设为自由,即水管之间采用柔性水管连接。
3) 铜冷却壁水管受到炉壳开孔约束时,水管发生弯折变形,在水管与炉壳开孔接触位置达到最大等效应力600 MPa,远超过纯铜的屈服强度,容易沿此位置发生屈服失效破损。因此,应避免铜冷却壁水管变形过程中接触炉壳开孔。
4) 铜冷却壁极限工作温度下水管末端位移量最大,此位置沿X向位移为1.23 mm,沿Y向位移为1.22 mm,它们的合位移为1.73 mm。因此,临界位移为1.73 mm。
5) 炉壳开孔直径设计中,在考虑到铜冷却壁安装误差及临界位移等因素的影响下,炉壳开孔直径应为120 mm。
| [1] | Wu T, Cheng S. Model of forming-accretion on blast furnace copper stave and industrial application[J]. Journal of Iron and Steel Research , 2012, 19 (7) : 1–5. DOI:10.1016/S1006-706X(12)60105-8 |
| [2] |
吴桐, 程树森.
高炉铜冷却壁合理操作建议[J]. 钢铁 , 2010, 46 (10) : 11–15.
WU Tong, CHENG Shusen. Recommendations on reasonable operation of BF copper stave[J]. Iron and steel , 2010, 46 (10) : 11–15. (in Chinese) |
| [3] |
马继文.
本钢五号高炉铜冷却壁破损原因分析及处理技术的研究[J]. 金属世界 , 2009 (6) : 26–28.
MA Jiwen. Bengang No.5 BF copper cooling stave damage cause analysis and processing technology of research[J]. Metal world , 2009 (6) : 26–28. (in Chinese) |
| [4] |
高福生.
本钢五号高炉铜冷却壁破损分析及改进[J]. 金属世界 , 2012 (4) : 33–36.
GAO Fusheng. Damaged analysis and improvement of No.5 blast furnace's copper cooling stave of bx steel[J]. Metal world , 2012 (4) : 33–36. (in Chinese) |
| [5] |
郇宜伟, 雷丽萍, 方刚, 等.
高炉铜冷却壁热力耦合的有限元分析[J]. 冶金设备 , 2009 (3) : 45–60.
HUAN Yiwei, LEI Liping, FANG Gang, et al. Thermo-mechanical coupling finite element analysis of blast furnace copper staves[J]. Metallurgical Equipment , 2009 (3) : 45–60. (in Chinese) |
| [6] |
章锐.
大型高炉冷却壁安装误差的控制[J]. 装备制造技术 , 2012 (2) : 161–177.
ZHANG Rui. Large sized blast furnace cooling stave installation error control[J]. Equipment Manufacturing Technology , 2012 (2) : 161–177. (in Chinese) |
| [7] | 石琳, 程树森.长寿高炉铸铜和铸铁冷却壁研究[D].北京:北京科技大学冶金学院, 2006. |
| [8] |
吴桐, 程树森.
高炉风口以上冷却壁的选择[J]. 钢铁研究学报 , 2012, 24 (8) : 16–20.
WU Tong, CHENG Shusen. Cooling stave selection above blast furnace tuyere[J]. Journal of Iron and Steel Research , 2012, 24 (8) : 16–20. (in Chinese) |
| [9] | 魏渊.高炉炉腹区域铸铜冷却壁数值模拟及热态试验方案研究[D].武汉:武汉科技大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10488-1014113762.htm |
| [10] |
李洋龙, 程树森.
铜冷却壁冷却恢复技术的传热过程[J]. 钢铁研究学报 , 2012, 24 (7) : 5–9.
LI Yanglong, CHENG Shusen. Cooling capacity recovery of copper stave based on heat transfer[J]. Journal of Iron and Steel Research , 2012, 24 (7) : 5–9. (in Chinese) |
| [11] |
刘增勋, 李哲, 柴清风, 等.
高炉铜冷却壁渣皮生长传热分析[J]. 钢铁 , 2010, 45 (8) : 12–15.
LIU Zengxun, LI Zhe, CHAIi Qingfeng, et al. Heat transfer analysis of slag skull growth for BF copper stave[J]. Iron and Steel , 2010, 45 (8) : 12–15. (in Chinese) |
| [12] |
石琳, 李志玲.
埋纯铜管铸铜冷却壁热态试验和热应力热变形研究[J]. 内蒙古大学学报 , 2009, 40 (6) : 699–707.
SHI Lin, LI Zhiling. A study on hot test and thermal stress and distortion of cast copper staves with buried copper pipes[J]. Journal of Inner Mongolia University , 2009, 40 (6) : 699–707. (in Chinese) |
| [13] | Shi L, Cao F, Zhang J.The study on hot test and thermal stress and distortion of cast copper staves with buried copper pipe[C]//2011 Second International Conference on Mechanic Automation and Control Engineering, July 15-17, 2011.Hohhot:IEEE, 2011:1822-1826. |
| [14] |
郑建春, 宗燕兵, 苍大强.
高炉铜冷却壁热态实验及温度场数值模拟[J]. 北京科技大学学报 , 2008, 30 (8) : 938–941.
ZHENG Jianchun, ZONG Yanbing, CANG Daqiang. Thermal test and numerical simulation of the temperature field of a blast furnace copper stave[J]. Journal of University of Science and Technology Beijing , 2008, 30 (8) : 938–941. (in Chinese) |
| [15] | Wu L J, Xu X, Zhou WG, et al. Heat transfer analysis of blast furnace stave[J]. International Journal of Heat and Mass Transfer , 2008, 51 (11/12) : 2824–2833. |
| [16] | AJ MacRae.Eddy-free tuyeres for a blast furnace[C]//AISTech-Iron and Steel Technology Conf Proc, October 19, 2010.Houston, Texas:[s.n.], 2010:489-498. |
 2015, Vol. 38
2015, Vol. 38


