COREX是由德国Korf公司和奥钢联(VAI)合作开发的一种使用块矿或球团矿作原料、使用煤作为主要还原剂和燃料的熔融还原炼铁工艺,是熔融还原工艺中最早商业化和工业化的工艺,具有流程短、工序少、污染轻等特点[1-3]。COREX主体设备由上部的预还原竖炉和下部的熔化气化炉组成。宝钢CORERX-3000的生产过程中,时常出现煤气流分布控制不合理的问题,影响了熔化气化炉的正常冶炼,使得煤气热利用和化学利用不佳,各项生产技术指标大幅下降[4-5]。熔化气化炉布料模式直接决定了料柱结构,进而影响到煤气流的分布,为解决煤气流分布不合理的问题,有必要针对熔化气化炉的布料模式进行重点研究。
前人已对高炉布料进行了详细研究,熔化气化炉的布料模式与高炉明显不同,它有煤万向节布料器和DRI-flap布料器两套布料系统,目前,对其布料规律的研究相对较少。笔者结合前人研究高炉及竖炉布料的方法[6-10],主要采用建立数学模型的方法对气化炉布料规律进行研究,同时考虑两个布料系统,建立料面形状预测模型。在此基础上,通过分析和考虑布料的影响因素及其特点,结合数学知识和计算机技术,开发了COREX-3000气化炉的料面预测仿真软件,可预测万向节布料器和挡板布料器的不同布料制度下形成的料流轨迹、落点位置以及料面形状,为现场选择和调整布料制度提供参考。
1 数学模型通过对物料在布料过程中的运动和受力分析,确定物料的落点位置;进一步根据物料的安息角和质量守恒,建立料面形状预测模型,该数学模型不考虑物料下行对料面的影响。模型分为万向节布料器模型,DRI-flap布料器模型和料面形状预测模型。
1.1 万向节布料器模型 1.1.1 物料出储料仓模型万向节布料器布料过程从物料流出储料仓开始,储料仓与万向布料器中心管部分之间连接的是一套螺旋排料装置,按照前人研究结果[9, 11],可知物料流出储料仓后进入中心管的速度V0与螺旋排料装置的转速与螺距相关,可由式(1)进行计算。
| $ {V_0} = {\omega _0}M, $ | (1) |
式中:M为螺旋排料器装置的螺距,m;ω0为螺旋排料器转速,圈/s。
1.1.2 物料沿中心喉管下落模型物料以水平速度V0从螺旋排料器流出后,沿中心喉管下落,此时竖直方向的初速度为0。物料与溜槽相碰后以初速度V1沿溜槽方向滑动,因物料下落时与中心喉管及溜槽发生碰撞,造成速度损失,故方程引入速度修正系数K,刘慰俭等[12]实验测定速度修正系数K为:焦炭0.70、烧结矿0.71,本文在计算时取K=0.71。
| $ {V_1} = K\cos \alpha {\left[{2g\left( {{H_0} + {h_0}} \right)} \right]^{0.5}}, $ | (2) |
式中:H0为中心喉管长度,h0为溜槽悬挂点至物料落点的距离。
1.1.3 物料在旋转溜槽上的运动模型物料在旋转溜槽的受力如图 1所示,诸力分别为:1) 重力G=mg;2) 离心力F=mω2lsin α;3) 支持力R=mgsin α-mω2lsin αcos α;4) 摩擦力:f=μR。由于溜槽转速较小,一般为6 r/min,故不考虑溜槽侧向对物料的摩擦力和由于旋转引起的科氏力[11]。
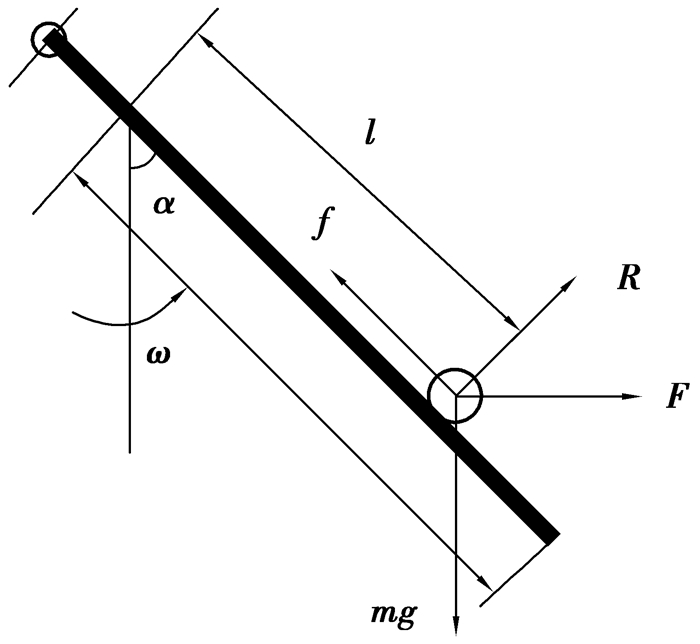
|
图 1 颗粒在溜槽上的受力分析 Figure 1 Force analysis of a particle on the chute |
沿溜槽方向,物料受力分析满足
| $ \sum F = mg\cos \alpha-\mu \left( {mg\sin \alpha-m{\omega ^2}l\sin \alpha \cos \alpha } \right) + m{\omega ^2}l\sin {\alpha ^2}。 $ | (3) |
根据牛顿第二定律进行转化并求解积分可得物料离开溜槽时的速度V2为:
| $ {V_2} = {\left[{{\omega ^2}\sin \alpha \left( {\sin \alpha + \mu \cos \alpha } \right){L^2} + 2g\left( {\cos \alpha-\mu \sigma \iota \nu \alpha } \right)L + V_1^2} \right]^{0.5}}, $ | (4) |
式中:ω为溜槽转速,rad/s;L为溜槽有效长度,m。
将V2用半径方向、竖直方向、切线方向上的分速度表示为:半径方向Vr=V2sin α;竖直方向:Vz=V2cos α;切线方向:Vθ=rcω。其中,rc为溜槽末端至炉喉中心的水平距离,m。
1.1.4 空区Coal料流模型物料在空区内受到重力、浮力和气体阻力的作用;浮力很小,不到重力的0.1%;相同条件下,颗粒越小,受到的气体阻力与重力的比值越大,在正常生产条件下,对于5 mm矿石,气体阻力小于重力的2%,对于10 mm的焦炭,气体阻力小于重力的3%,气化炉一般使用块煤粒度都较大,因此,本文忽略煤气阻力[13]。
颗粒运动方程应满足牛顿第二定律:
| $ -\frac{{{\rm{d}}z}}{{{\rm{d}}{t^2}}} = g。 $ | (5) |
求解积分,可得物料在空区的运动时间t:
| $ t = \left( {-{V_2}\cos \alpha + \sqrt {{{\left( {{V_2}\cos \alpha } \right)}^2} + 2g{h_{\rm{t}}}} } \right)/g, $ | (6) |
式中,ht为溜槽下沿到料线的距离。
物料到达料面上的速度V3为:
| $ {V_3} = \sqrt {V_2^2 + 2g{h_{\rm{t}}} + {{\left( {\omega {r_{\rm{c}}}} \right)}^2}} 。 $ | (7) |
物料离开溜槽后,在炉喉半径方向的运动距离为:
| $ {r_{\rm{j}}} = {r_{\rm{c}}} + \left( {{V_2}\sin \alpha } \right)t。 $ | (8) |
物料在切线方向上的运动距离:
| $ {r_{\rm{q}}} = \omega {r_{\rm{c}}}t, $ | (9) |
由方程(8)和(9)可以求出物料落点离气化炉中心线距离r:
| $ r = \sqrt {r_{\rm{j}}^2 + r_{\rm{q}}^2} = \sqrt {{{\left( {r + \left( {{V_2}\sin \alpha } \right)t} \right)}^2} + {{\left( {\omega {r_{\rm{c}}}t} \right)}^2}} 。 $ | (10) |
DRI-flap布料器结构如图 2所示,物料先后经垂直中心管下落、倾斜管滑落、挡板碰撞三个过程,通过牛顿第二定律建立这三个过程的数学模型。
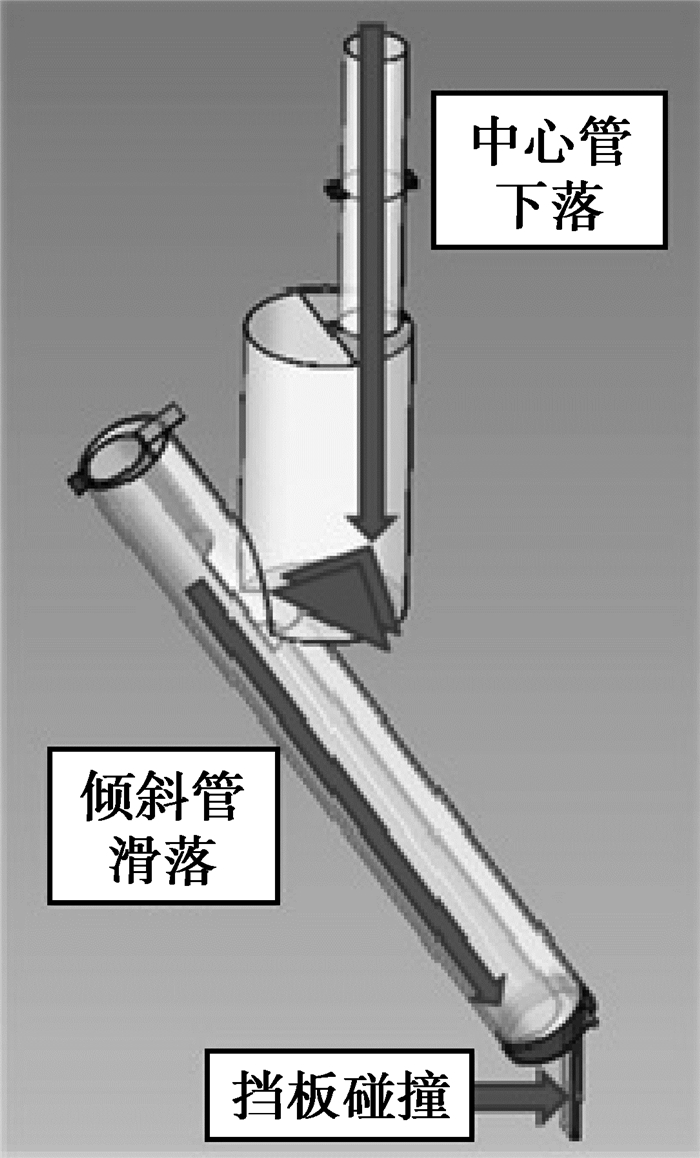
|
图 2 DRI-flap布料器示意图 Figure 2 Schematics of DRI-flap distributor |
布料过程从物料出储料仓开始,储料仓与DRI布料器的连接部分是一螺旋排料装置,根据螺旋转速和螺距计算初始物料水平速度V0。物料的积累使得缓冲管底部形成一个死角区域,物料下落到缓冲管底部与死角区域的物料碰撞后进入倾斜管,与倾斜管再次碰撞后以初速度V1沿倾斜管滑动。与万向布料器类似,方程引入速度修正系数KDRI,其物理意义为颗粒下落过程由于碰撞造成的速度衰减。
| $ {V_1} = {K_{{\rm{DRI}}}}\cos {\alpha _1}\sqrt {2g\left( {{H_1} + {h_1}} \right)}, $ | (11) |
式中:KDRI为速度修正系数;H1为下降管有效长度,m;h1为缓冲管有效长度,m;α1为倾斜管与竖直方向的夹角,(°)。
1.2.2 物料在倾斜管中运动模型与倾斜管相碰后的物料以初速度V1沿倾斜管滑动,在倾斜管上受力与旋转溜槽相似,由于倾斜管固定,故无离心力的作用,物料在倾斜管上只受重力G=mg、支持力R=mgsin α1、摩擦力f=μ1R。设定物料流出倾斜管的速度为V2,则
| $ {V_2} = \sqrt {V_1^2 + 2g\left( {\cos {\alpha _1} + {\mu _1}\sin {\alpha _1}} \right){L_1}}, $ | (12) |
式中:α1为倾斜管与竖直方向的夹角,(°);L1为倾斜管道出口位置与物料在倾斜管道内碰撞点的距离,m;μ1为物料与倾斜管道的摩擦系数。
1.2.3 DRI挡板碰撞模型图 3是不同挡板角度下物料碰撞后运动轨迹示意图,挡板角度(与水平方向夹角)为αDRI,物料与挡板碰撞前与挡板的夹角为α2,本文采用“DEM碰撞”原则[14],碰撞后物料与挡板夹角为α3,则物料运动方向与竖直方向的夹角为:
| $ {a_4} = \left( {90-{\alpha _{{\rm{DRI}}}}} \right)-{\alpha _3} $ | (13) |
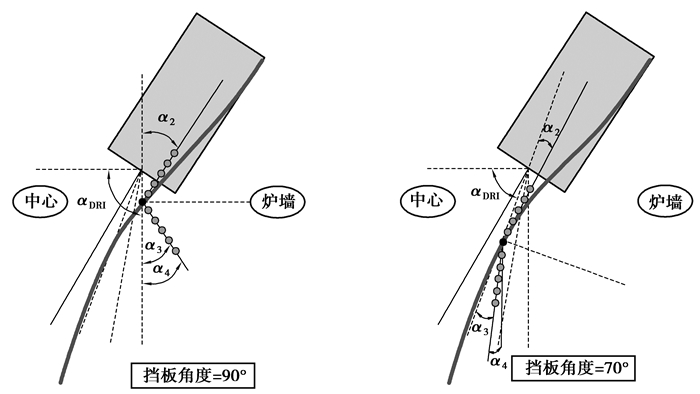
|
图 3 物料与挡板碰撞后的运动方向判断原理 Figure 3 Principle of judgment direction after colliding between burden and flap |
若α4为正值,表明运动方向指向炉内中心;反之,运动方向指向炉墙方向。
物料以V2的速度与挡板发生碰撞后,以V3的速度弹开,本模型给出一个修正系数K2,其物理意义为颗粒与挡板碰撞后造成的速度衰减。
| $ {V_3} = {K_2}{V_2}。 $ | (14) |
物料在空区只受重力作用,故半径方向的速率不变,碰撞点与料面垂直高度为H2。
半径方向速度:V3sin α4;
垂直方向速度:
DRI-flap布料器挡板末端距离料面的距离为ht,则对于物料在空区运动的时间t1,有
| $ {h_{\rm{t}}}{\rm{ = }}{V_{{\rm{z1}}}}{t_1} + 0.5gt_1^2。 $ | (15) |
求解式(15)可得:
| $ {t_1} = \left( {\sqrt {V_{Z1}^2 + 2g{h_{\rm{t}}}}-{V_{{\rm{z1}}}}} \right)/g。 $ | (16) |
物料落点距离气化炉中心线距离r1为
| $ {r_1} = {V_3}{t_1}\sin {\alpha _4}。 $ | (17) |
采用多条线段组合描述料面形状[9],线段斜率的绝对值等于或小于物料自然堆角,直线之间的交点即为料堆的堆尖或堆脚。
| $ f\left( r \right) = {K_n}\left( {r-{r_0}} \right) + {f_0}\left( r \right), $ | (18) |
式中:r为径向上离炉喉中心的距离,r0,f0(r)为料面函数某段的端点坐标,Kn为第n段直线的斜率。
2 数学模型的运用根据建立的COREX-3000熔化气化物料面形状的数学模型,利用VB语言开发了COREX-3000气化炉的料面预测仿真软件,可预测万向节布料器和DRI-flap布料器在不同布料制度下形成的料流轨迹、落点位置以及料面形状,为现场选择和调整布料制度提供参考。
2.1 万向节布料器布料落点位置变化规律基于建立的数学模型,同时参考前人物理实验与数值模拟的结果[14-16],计算得出料线高度、溜槽角度、档位半径之间的关系,图 4为料线高度12、14 m时溜槽角度与落点位置、物料速度之间的关系。由图 4可知,溜槽角度不变的情况下,料线高度越大,落点位置对应的档位半径越大。物料流出溜槽末端速度和到达料面处的终点速度均随溜槽角度增加呈现减小趋势,而物料流出溜槽末端的水平速度却呈现增加趋势,正是由于溜槽末端水平速度随溜槽角度增加而增加,导致了物料到达料面处时水平外移距离的增加,进而产生随溜槽角度增加外堆角逐渐较小的现象。
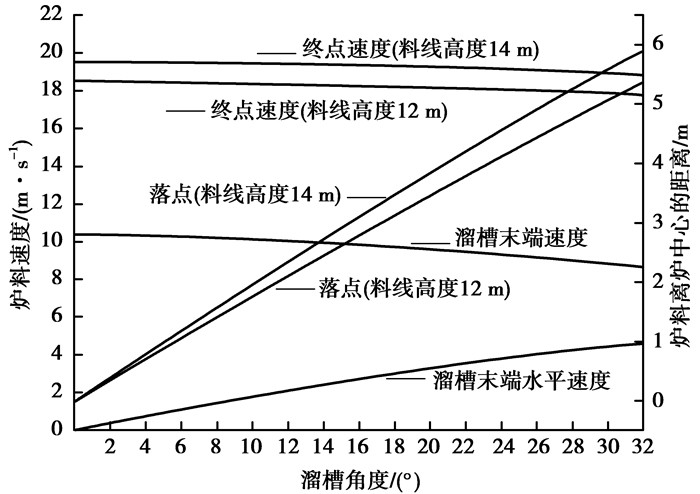
|
图 4 料线高度、溜槽角度、档位半径之间的关系 Figure 4 Relations among burden line, chute angle and gear radius |
图 5为该软件计算的COREX-3000现场的料线高度为14 m时落点位置与挡板角度的关系图。COREX熔化气化炉的挡板布料器的安装位置距炉内中心线的距离是4.515 m,经计算发现挡板角度为82.5°时,物料与挡板发生碰撞后垂直下落,落点位置是4.5 m。这一位置恰恰是挡板布料器的转折点,挡板角度小于82.5°,物料向炉内中心方向移动,挡板角度大于82.5°,物料被弹回,向炉墙方向移动。
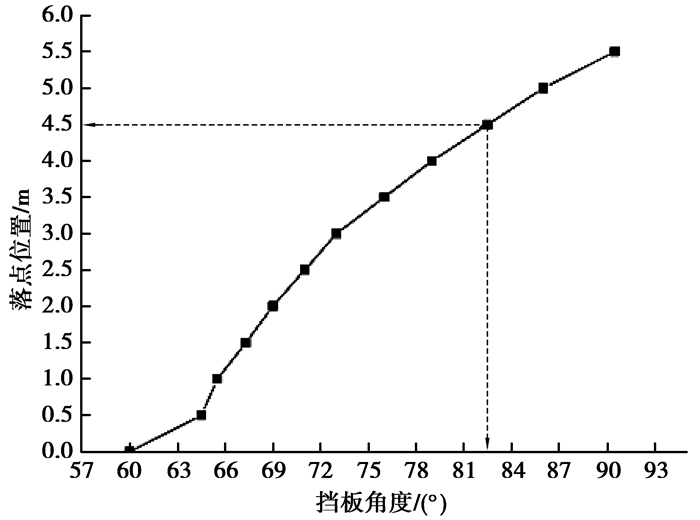
|
图 5 不同挡板角度下的落点位置图 Figure 5 Impact position under different flap angles |
该模型具备预测不同布料制度下多批次混合布料料面形状的功能,下面对现场某一布料制度下的料面形状进行预测。
步骤1) 设定档位。根据现场提供的某一布料制度下的布料参数,设定加入料批的档位数和档位相对厚度,软件可根据各档位的相对厚度计算出该档位的布料体积,为料面形状的计算做准备。图 6为本次布料的参数。
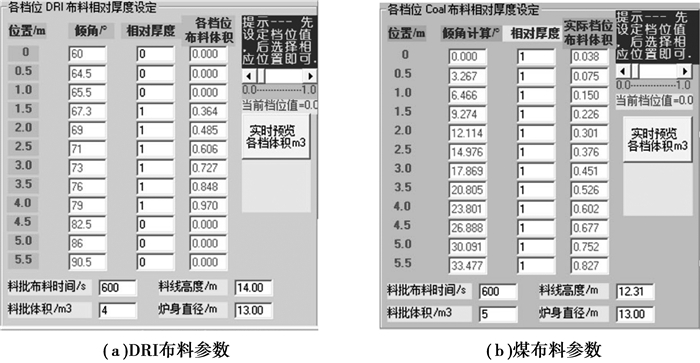
|
图 6 现场布料参数 Figure 6 The actual charging parameters |
步骤2) 预测料面形状。由步骤1) 得到的各档位的布料体积,再根据各档位的体积守恒以及内外堆角的大小,计算出堆尖和堆角的位置,再由多条线段连接组成该次布料下的料面形状,如图 7所示。
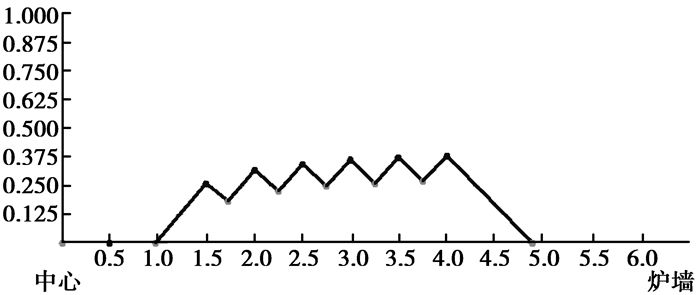
|
图 7 第一批物料布料后的料面形状图 Figure 7 Burden pile profile after the first charging |
步骤3) 下一批物料选择及计算。以步骤2) 所得的料面为下一批布料的初始料面,重复操作步骤1) 和步骤2),即可获得多批次混合布料的料面形状,如图 8所示。
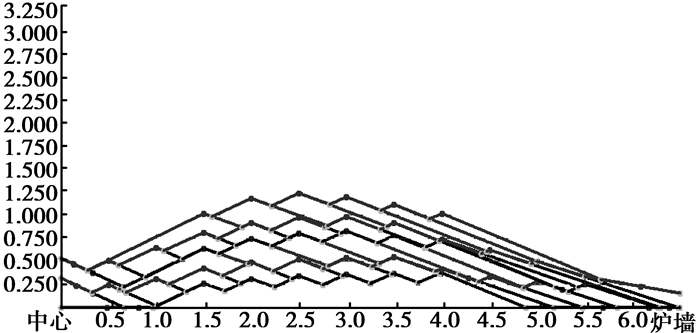
|
图 8 多批物料混合布料时料面形状图 Figure 8 Burden pile profile under multi-batches mixed charging |
1) 鉴于COREX气化炉与高炉布料系统的不同,同时考虑了DRI布料和煤布料两个布料系统。分别分析物料在两个布料器上的运动和受力情况,建立了万向节布料器模型和DRI布料器模型。
2) 根据物料的落点位置、内外堆角及该档位物料的体积建立料面形状预测模型,该模型用多条线段组合表示料面形状。
3) 根据建立的料面形状预测模型,结合现场提供数据及物理模拟,开发了料面形状预测软件,可预测不同布料模式下的料流轨迹、落点位置及料面形状,为现场选择和调整布料制度提供参考。
| [1] | Qu Y, Zou Z, Xiao Y. A Comprehensive Static Model for COREX Process[J]. ISIJ International , 2012, 52 (12) : 2186–2193. DOI:10.2355/isijinternational.52.2186 |
| [2] | Kumar P P, Gupta P K, Ranjan M. Operating experiences with Corex and blast furnace at JSW Steel Ltd[J]. Ironmaking & Steelmaking , 2008, 35 (4) : 260–263. |
| [3] |
李强, 张玉栋, 张丽娟, 等.
COREX竖炉布料规律的数学模型[J]. 东北大学学报:自然科学版 , 2011, 32 (11) : 1591–1594.
LI Qiang, ZHANG Yudong, ZHANG Lijuan, et al. Mathematical model of burden distribution law for COREX shaft[J]. Journal of Northeastern University:Natural Science , 2011, 32 (11) : 1591–1594. (in Chinese) |
| [4] |
李维国.
COREX-3000生产现状和存在问题的分析[J]. 宝钢技术 , 2008 (6) : 11–18.
LI Weiguo. Operation status quo and technical problems of COREX-3000[J]. Baosteel Technology , 2008 (6) : 11–18. (in Chinese) |
| [5] |
朱仁良, 朱锦明, 宋文刚.
宝钢COREX-3000运行现状及发展前景[J]. 宝钢技术 , 2012 (6) : 12–17.
ZHU Renliang, ZHU Jinming, SONG Wengang. Present operation situation and development prospect of Baosteel COREX-3000[J]. Baosteel Technology , 2012 (6) : 12–17. (in Chinese) |
| [6] | Ueda S, Natsui S, Nogami H, et al. Recent progress and future perspective on mathematical modeling of blast furnace[J]. ISIJ international , 2010, 50 (7) : 914–923. DOI:10.2355/isijinternational.50.914 |
| [7] | Zhou H, Luo Z G, Zhang T, et al. 3D numerical simulation of the influence of AGD beams on gas distribution in COREX-3000 shaft furnace[J]. Advanced Materials Research , 2013, 712 : 1268–1273. |
| [8] | Mio H, Komatsuki S, Akashi M, et al. Effect of chute angle on charging behavior of sintered ore particles at bell-less type charging system of blast furnace by discrete element method[J]. ISIJ International , 2009, 49 (4) : 479–486. DOI:10.2355/isijinternational.49.479 |
| [9] |
于要伟, 白晨光, 梁栋, 等.
无钟高炉布料数学模型的研究[J]. 钢铁 , 2008, 43 (11) : 26–30.
YU Yaowei, BAI Chenguang, LIANG Dong, et al. A mathematical model for bell-less top charging[J]. Iron and Steel , 2008, 43 (11) : 26–30. (in Chinese) |
| [10] |
国宏伟, 张建良, 陈令坤, 等.
高炉无钟布料仿真系统[J]. 过程工程学报 , 2009, 9 (S1) : 415–419.
GUO Hongwei, ZHANG Jianliang, CHEN Linkun, et al. Simulation of charging system in bell-less BF[J]. The Chinese Journal of Process Engineering , 2009, 9 (S1) : 415–419. (in Chinese) |
| [11] | 刘云彩. 高炉布料规律[M]. 北京: 冶金工业出版社, 2005 : 1 -27. |
| [12] |
刘慰俭, 叶肇宽.
无料钟高炉炉顶设备中布料的研究[J]. 钢铁 , 1983, 18 (5) : 1–7.
LIU Weijian, YE Zhaokuan. An experimental study on the distribution of materials in a bell-less furance top[J]. Iron and Steel , 1983, 18 (5) : 1–7. (in Chinese) |
| [13] |
王平.
串罐无料钟料流轨迹与宽度测定及其分析[J]. 钢铁 , 2003, 38 (3) : 8.
WANG Ping. Measurement and analysis of burden flow trajectory and width in bell-less top with two concentric vertical hoppers[J]. Iron and Steel , 2003, 38 (3) : 8. (in Chinese) |
| [14] | Li H, Luo Z, Zou Z, et al. Mathematical simulation of burden distribution in COREX melter gasifier by discrete element method[J]. Journal of Iron and Steel Research, International , 2012, 19 (9) : 36–42. DOI:10.1016/S1006-706X(13)60006-0 |
| [15] |
李海峰, 罗志国, 张树才, 等.
溜槽角度对混装布料过程的影响[J]. 东北大学学报:自然科学版 , 2012, 33 (5) : 681–684.
LI Haifeng, LUO Zhiguo, ZHANG Shucai, et al. Effect of chute angle on process of mixing charging[J]. Journal of Northeastern University:Natural Science , 2012, 33 (5) : 681–684. (in Chinese) |
| [16] |
陈立胜, 罗志国, 游洋, 等.
挡板角度对挡板布料器布料过程的影响[J]. 东北大学学报:自然科学版 , 2013, 34 (7) : 971–974.
CHEN Lisheng, LUO Zhiguo, YOU Yang, et al. Effects of flap angles on the charging procedure of flap distributors[J]. Journal of Northeastern University:Natural Science , 2013, 34 (7) : 971–974. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38


