2. 武汉科技大学 钢铁冶金及资源利用省部共建教育部重点实验室,武汉 430081;
3. 武汉钢铁(集团)公司,武汉 430083
2. Key Laboratory of Ferrous Metallurgy and Resources Utilization, Ministry of Education, Wuhan University of Science and Technology, Wuhan 430081, P.R.China;
3. Wuhan Iron and Steel Company, Wuhan 430083, P. R. China
随着工业化发展对钢的质量要求越来越高,洁净钢和纯净钢的生产越来越普及,由于钢中夹杂物不仅会降低钢的塑性、韧性和疲劳寿命,使钢的加工性能变坏,且对钢材表面光洁度和焊接性能也有直接影响。而中间包作为钢液进入结晶器凝固成铸坯之前的最后一个冶金容器,可以提高钢水温度和成分的均匀性,改善钢液的流动状态,延长钢液在中间包内的停留时间,促进夹杂物上浮以达到去除的目的,故中间包冶金备受冶金工作者的关注。合理设计和安装湍流控制器、坝以及堰等控流装置,优化中间包内钢液的流动状态,最大限度地去除中间包内的夹杂物,提高钢液的洁净度成为中间包冶金研究的重点。Tomasz[1]等的研究表明:安装湍流控制器可以改善钢液流经中间包的混合动力学条件以及水动力条件,获得优质铸坯。文献[2-4]研究了坝对中间包钢液流动特性和夹杂物去除的影响,结果表明中间包能显著改善钢液的流动状态,延长钢液的运动轨迹,使钢液向中间包液面流动,促进夹杂物的去除,且合适的坝高度可以保证钢液面的稳定而不卷渣。李宁等[5]研究表明:设置堰有利于延长钢液的运动轨迹,但增加了死区体积比;合理的堰到长水口间距以及堰深可控制死区体积比,能抑制大型夹杂物进入浇注区。也有许多学者[6-10]对湍流控制器、坝、堰之间的组合,以及堰深、坝高、坝堰间距、堰到长水口间距等中间包控流参数进行了深入研究,针对其研究的中间包提出了合适的控流参数值。由于各个厂中间包结构等设计的不同,导致这些影响因素也千差万别,目前还没有一种合理的方案适用于所有的中间包。
某钢厂55 t两流板坯连铸中间包采用湍流控制器控流,其流场不合理,钢液在中间包内停留时间短,死区体积分数较大,夹杂物去除率低,导致产品中夹杂物超标,有时会引起钢板表面质量缺陷。本实验以此钢厂中间包为研究对象,通过物理模型实验,研究了中间包的不同坝、堰结构组合以及安装位置对中间包流体流动特性的影响,优化出合适的结构,以确保超低碳钢的质量,为实际生产提供参考依据。
1 物理模型的建立 1.1 实验原理物理模型实验的理论基础是相似原理,一般要求同时满足几何相似和动力学相似以保证模型和原型相似。对于几何相似,只要模型与原型具有一定的相似比λ即可;对于动力学相似,由于中间包内钢液的流动涉及的作用力主要是惯性力、重力和黏性力,这些力的定性准数为雷诺准数(Re)及弗劳德准数(Fr)。相似理论认为,当模型与原型的Re处于第二自模化区(Re的第二自模化区的临界值为1×104~1×105)时,流动状态、流速分布与Re无关[11]。经计算,模型与原型的Re都已经处于第二自模化区,故只要保证Fr相等即可保证动力相似,即
| $ F{r_{\rm{m}}} = \frac{{u_{\rm{m}}^2}}{{{g_{\rm{m}}}{L_{\rm{m}}}}}{\rm{ = }}\frac{{u_{\rm{p}}^2}}{{{g_{\rm{p}}}{L_{\rm{p}}}}}{\rm{ = }}F{r_{\rm{p}}}, $ | (1) |
式中:u为流体速度,m/s;L为特征长度,m;g为重力加速度,m/s2;下标m代表模型(model),p代表原型(prototype)。
由于相似比λ=Lm/Lp,流量Q=πud2/4,时间t=L/u,代入式(1)可得以下模型与原型相关参数的关系:
| $ {Q_{\rm{m}}} = {(\lambda )^{5/2}}{Q_{\rm{p}}}, $ | (2) |
| $ {t_{\rm{m}}}{\rm{ = }}{(\lambda )^{1/2}}{t_{\rm{p}}}, $ | (3) |
式中:d为出水口直径,m;Q为流量,m3/s; t为时间,s。
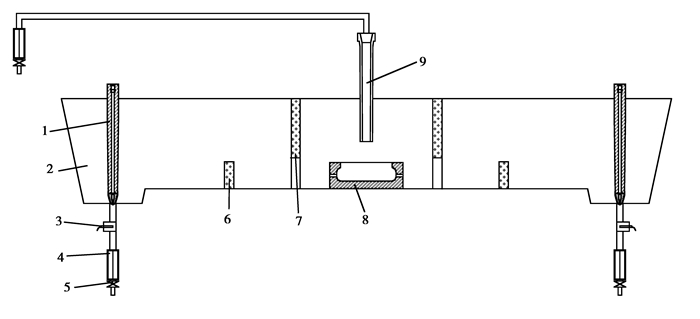
1.2 实验装置实验所用的中间包模型是按模型与原型1:3的比例用15 mm厚的有机玻璃制成。实验装置如图 1所示。
|
图 1 中间包水模型实验装置图 Figure 1 Schematic of tundish water model experiment (1-塞棒;2-中间包;3-电导电极;4-流量计;5-阀门; 6-坝;7-堰;8-湍流控制器;9-长水口) |
现场铸坯断面尺寸为1 100 mm×230 mm,拉速为1.30 m/min,通过塞棒控制中间包流量。原型与模型主要参数如表 1所示。
| 表 1 原型与模型相关尺寸 Table 1 Corresponding dimensions of prototype and water model |
中间包模型有效体积V为0.304 6 m3。当流体连续、稳定的流过中间包时,可计算出中间包的理论停留时间为
| $ \;{t_a} = \frac{V}{{{Q_{\rm{m}}}}}。 $ | (4) |
将体积V为0.304 6 m3,模型流量Qm为3.52×10-4m3/s代入式(4)得ta为433 s,即中间包的理论停留时间为433 s。
2 实验方法及过程 2.1 流场显示本实验采用示踪剂法观察中间包内流体的流动状态。当中间包内的流场达到稳定状态时,在中间包长水口内瞬间注入亚甲基蓝溶液,并用摄像机拍摄中间包内的流体流动过程。
2.2 停留时间分布(RTD)曲线的测定方法实验采用“刺激-响应”方法测定RTD曲线。当中间包内流体流动稳定时,在中间包长水口处迅速注入300 mL饱和的NaCl溶液作为刺激信号。用DDLY-2005型电导率仪通过电导电极测量中间包出水口处的电导率,后经DJ800型多功能监测系统传输到计算机,由计算机预设的程序自动采集数据。数据经过处理可得到中间包的RTD曲线,从曲线可得加入示踪剂到出水口开始出现示踪剂的滞止时间tmin,以及示踪剂浓度达到最大的峰值时间tmax,然后算出钢液在中间包的平均停留时间。根据Sahai[12]提出的修正混合流动模型,计算出中间包死区体积分数Vd、活塞区体积分数Vp以及全混区体积分数Vm。
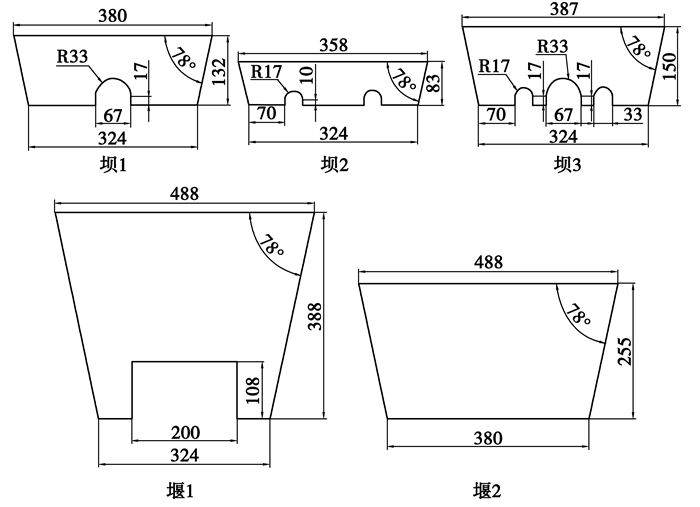
2.3 实验实施方案实验中所用坝、堰结构的主视图如图 2所示。
|
图 2 中间包坝、堰设计图 Figure 2 Design drawing of weir and dam of tundish |
实验过程先设计了7种方案,其中湍流控制器不加坝、堰为空白对照组,命名为0;另外6种控流方案为湍流控制器加不同坝、堰结构组合,分别按照坝堰序号进行命名,如1-1表示坝1跟堰1组合的方案,以此类推,表 2为各方案及其对应命名。实验过程中坝到堰的距离为256 mm,堰到长水口的距离为283 mm,坝、堰厚27 mm;安装时,坝是紧贴中间包底,堰则上端与中间包顶部平齐。
| 表 2 坝、堰设计方案及其对应的命名 Table 2 Design scheme of weir and dam and its corresponding name |
根据上述实施方案得到最优的坝、堰结构,以坝堰间距和堰到中间包长水口的间距作为中间包控流参数进行实验。实验过程中坝堰间距、堰到长水口间距参数如表 3所示。
| 表 3 中间包控流参数 Table 3 Parameters of flowing control in tundish |
针对拍摄的流场照片,截取不同时间的图片,观察了流场演变的过程。图 3为湍流控制器不加坝、堰方案的流体流动状态的照片, 图 4为湍流控制器跟坝堰组合方案中一组具有代表性的流体流动状态的照片。

|
图 4 坝1、堰1组合的中间包不同时刻的流体流动状态 Figure 4 Flow state of fluid in tundish at different time with No. one weir and dam |

|
图 3 不加坝、堰的中间包不同时刻的流体流动状态 Figure 3 Flow state of fluid in tundish at different time without weir and dam |
从图 3可以看出,注入亚甲基蓝溶液后,流体首先冲击到湍流控制器的底部,并且迅速铺开,由于湍流控制器内壁的阻挡,流体沿着湍流控制器的内壁向上运动,流出湍流控制器。流出的流体,一部分由向下的冲击流体的带动向底部流去,而大部分则流向中间包表层。流体流动到表层后向四周铺开,在浇注区因出水口的抽吸,直接流向出水口。从加入指示剂开始到指示剂开始流出中间包用了65 s。
而从图 4可以看出,注入亚甲基蓝溶液后,流体流动状态与不加坝堰的流动状态在前6 s是相同的,不过在8 s时由于堰的阻挡,开始向下流动并穿过堰下面的泄流孔流向坝。从20 s时的图可以看出流体在注入流区内混合较充分,这是由于堰的存在,把流体限制在注入流区内,新注入到中间包的流体在此区域可以充分混合、均匀。流体碰到坝之后,小部分经过坝上的泄流孔,流向浇注区;大部分流体受坝的抬升,方向发生改变,液体流向中间包表层。流体越过坝后,并没有因出水口的抽吸直接流向水口,而是保持一定的流速冲击中间包侧壁后流向出水口,从加入指示剂开始到指示剂开始流出中间包用了90 s。
可见坝堰组合之后的确可以改变流体的流动状态,延长流体运动的轨迹,避免短路流的产生,提高了液体的平均停留时间,减小死区体积分数,促进夹杂物的上浮去除。从图 4还可以看出,在流体经过坝、堰之后有部分地方的颜色较浅,说明这些地方存在了一定体积的死区。
3.2 坝、堰对中间包内钢液停留时间的影响对上述7种不同方案进行RTD实验,并根据所测的RTD数据,计算出不同方案下中间包内流体的滞止时间、峰值时间、平均停留时间,以及活塞区、死区、全混流区的体积分数,其结果如表 4所示。
| 表 4 RTD曲线计算的实验结果 Table 4 Experimental results of RTD curves |
从表 4可以看出,方案1-1的平均停留时间最大,为299 s,死区体积分数最小,为31.0%;而不加坝堰组合方案0的停留时间次之,为286 s,死区体积分数为34.0%,比其他方案都好。由此可见,虽然坝、堰组合可以改变流体的流动状态,避免短路流的出现,但是设计和安装不合理,反而会增加中间包内死区的体积分数。
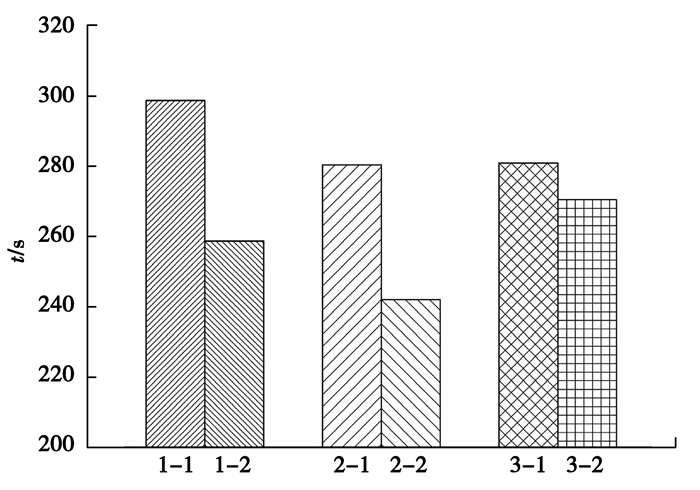
图 5为不同方案下中间包平均停留时间(t)。从图 5中可以得出:堰1各组方案中的停留时间都大于对应堰2各组方案中的停留时间。这与堰的结构有关,堰1到中间包底部间距小于堰2到中间包底部间距,可以将冲击湍流限制在注入流区,使其混匀更充分,并且使在中间包底部流动的钢液更能有效带动坝前死区的钢液流向表面,相对延长中间包的停留时间,减小死区体积分数,促进夹杂物上浮去除;而单从堰1中的3组方案看,坝的结构对平均停留时间也有较大影响。3种坝中泄流孔虽然不同,但从图 4可以看出,流经泄流孔的钢液很少,大部分钢液越过坝流向出水口。坝若过低,则向上的钢液还未流向表面就被水口流卷吸进去,降低了中间包的平均停留时间;坝若过高,则向上的钢液流向表面,易造成液面波动,且增大了坝后面的死区体积分数,缩短平均停留时间。故在此实验下,坝1、堰1结构组合更合理。
|
图 5 不同控流方案下中间包平均停留时间 Figure 5 Average residence time of different flow control scheme in tundish model |
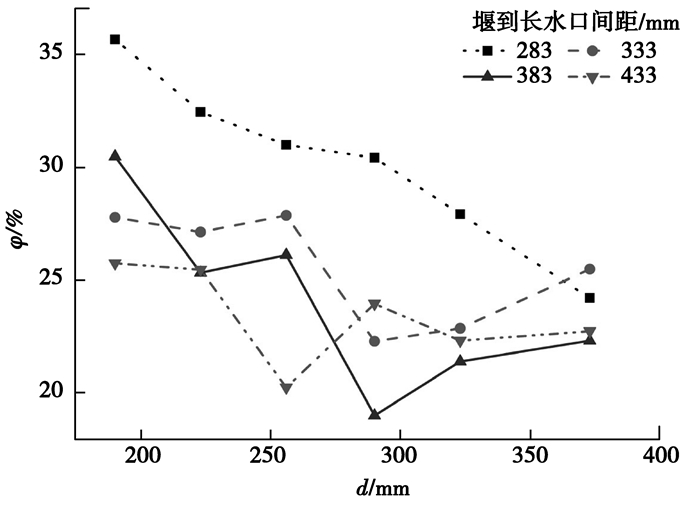
在优化后的坝、堰组合下,改变控流参数进行了进一步的实验。图 6为坝堰间距及堰到长水口间距(d)对中间包死区体积分数(φ)的影响。
|
图 6 坝堰间距以及堰到长水口间距对死区体积分数的影响 Figure 6 Effect of distance between weir and dam and distance between weir and the long nozzle on volume fraction of dead zone |
由图 6可以看出,在堰到长水口间距为283 mm时,中间包死区的体积分数随着坝堰间距的增大而减小;而在堰到长水口间距为333、383、433mm时,中间包死区的体积分数随着坝堰间距的增大,其大体趋势是先减小后增大。这是因为堰坝间距较大时,坝对钢液的抬升作用较弱,容易在堰后面形成较大体积的死区;而坝堰间距较小时,坝的抬升作用太强,使钢液向中间包表层流动的趋势增强,虽然可以提高钢液的平均停留时间,但是在坝后面会形成较大体积的死区[5]。因此,坝堰间距要适当。本实验在坝堰间距为290 mm,堰到长水口间距为383 mm时最佳,其平均停留时间为351 s,死区体积分数为19.0%,相对不加坝堰的方案0,其平均停留时间增加了65 s,死区体积分数减小了15.0%。
3.3 优化前后的RTD曲线对比由上述对中间包平均停留时间和死区体积分数的分析可知,坝1、堰1结构在坝堰间距290 mm,堰到长水口间距383 mm时最佳。为了便于直观了解控流装置对中间包流场的影响,将不加坝、堰方案与其进行对比分析。图 7为两种方案下的RTD曲线。
|
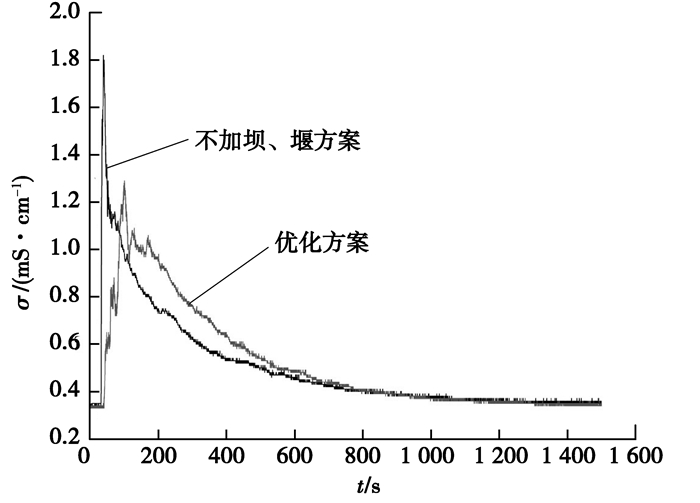
图 7 不同方案的RTD曲线 Figure 7 RTD curves of different scheme |
从图 7可知,在不加坝、堰情况下,中间包的RTD曲线尖锐,其响应时间为33 s,峰值时间为47 s;而优化方案下,中间包的RTD曲线尖锐程度明显改善,其响应时间为39 s,峰值时间为98 s,均比不加坝、堰情况下时间长。这是因为加入坝、堰后,中间包内流场得到了改善,流体流动轨迹延长,从而提高了流体在中间包内的停留时间。从图中还可以看出,优化方案峰值的电导率(σ)明显小于不加坝、堰情况下峰值的电导率。由于堰对注入流区的限制,使流体在注入流区得以充分混匀,故其电导率较小。因此,采用优化方案后,改善了中间包内的流场,使流体混匀更充分,提高了中间包内的停留时间,减小了死区的体积分数,促进夹杂物的上浮去除。
3.4 夹杂物上浮临界直径的计算由于钢液在中间包内的流动处于湍流状态,其Re>500,故夹杂物上浮服从Newton公式[13]:
| $ {v_{{\rm{in}}}}{\rm{ = }}{\left( {\frac{{3.03{d_{{\rm{in}}}}({\rho _{\rm{s}}}-{\rho _{{\rm{in}}}})g}}{{{\rho _{\rm{s}}}}}} \right)^{1/2}}, $ | (5) |
式中:vin为夹杂物上浮速度,m/s;din为夹杂物直径,μm;ρs为钢液密度,7.08×103kg/m3;ρin为夹杂物的密度,3.40×103kg/m3。
优化实验的最短停留时间为39 s,由tm=λ1/2tp得:tp=67 s。在原型最短停留时间67 s内,夹杂物上浮最小直径由式(5)计算得:
| $ {v_{{\rm{in}}}} = \frac{{1.1}}{{67}} = {\left( {\frac{{3.03{d_{{\rm{in}}}}(7.08-3.40) \times {{10}^3} \times 9.8}}{{7.08 \times {{10}^3}}}} \right)^{1/2}}。 $ | (6) |
式中:1.1 m为原型中间包钢液深度。
由式(6)得,din=17.5 μm。即计算结果表明:优化方案中间包内直径大于17.5 μm的夹杂物都能上浮去除。在实际生产过程中,夹杂物还能因碰撞聚集而发生长大,更容易上浮去除。
4 结论1) 坝、堰组合之后可以改变流体的流动状态,延长流体运动的轨迹,与没有坝、堰相比,提高了液体的平均停留时间,但在流体经过坝、堰后都存在一定体积的死区;其中坝1、堰1结构组合方案相对其他方案更佳,其停留时间最大,为299 s,死区体积分数最小,为31.0%。
2) 改变控流参数进一步实验后,坝1、堰1方案在坝堰间距为290 mm,堰到长水口间距为383 mm时最佳,流体在中间包内的平均停留时间为351 s,死区体积分数为19.0%,比不加坝堰的方案0,平均停留时间增加了65 s,死区体积分数减小了15.0%。
3) 由Newton公式计算表明,此优化方案中间包去除夹杂物的临界直径为17.5 μm,在351 s内夹杂物均能上浮去除。
| [1] | Tomasz M, Jacek P. Optimization of two-strand industrial tundish work with use of turbulence inhibitors: physical and numerical modeling[J]. Steel Research International , 2012, 83 (11) : 1029–1038. DOI:10.1002/srin.v83.11 |
| [2] | Pradeep K J, Srinivasa R, Anupam D. Effect of height and position of dams on inclusion removal in a six strand tundish[J]. Journal of the Iron and Steel Institute of Japan International , 2008, 48 (2) : 154–160. DOI:10.2355/isijinternational.48.154 |
| [3] |
李怡宏, 赵立华, 包燕平, 等.
板坯中间包内钢液流动特性[J]. 北京科技大学学报 , 2014, 36 (1) : 21–28.
LI Yihong, ZHAO Lihua, BAO Yanping, et al. Flow characteristic of molten steel in slab casting tundishes[J]. Journal of University of Science and Technology Beijing , 2014, 36 (1) : 21–28. (in Chinese) |
| [4] |
苑品, 包燕平, 崔衡, 等.
高品质IF钢连铸中间包降低残钢量的水模型研究[J]. 北京科技大学学报 , 2011, 33 (supplement 1) : 1–5.
YUAN Pin, BAO Yanping, CUI Heng, et al. Water model research on decreasing the casting remnant of high quality IF steel[J]. Journal of University of Science and Technology Beijing , 2011, 33 (supplement 1) : 1–5. (in Chinese) |
| [5] |
李宁, 包燕平, 林路, 等.
挡渣墙对板坯连铸中间包流场的影响研究[J]. 钢铁钒钛 , 2014, 35 (3) : 83–87.
LI Ning, BAO Yanping, LIN Lu, et al. Research on the effect of slag wire on fluid flow in tundish for slab continuous casting[J]. Iron Steel Vanadium Titanium , 2014, 35 (3) : 83–87. (in Chinese) |
| [6] |
文光华, 唐萍, 祝明妹, 等.
板坯连铸中间包钢液洁净度的水力学模拟和应用[J]. 特殊钢 , 2004, 25 (1) : 9–11.
WEN Guanghua, TANG Ping, ZHU Mingmei, et al. Hydraulics simulation and application on cleanliness of liquid steel in tundish for slab concasting[J]. Special Steel , 2004, 25 (1) : 9–11. (in Chinese) |
| [7] | Moumtez B, Ahmed B, Kamel T. Numerical investigation of the fluid flow in continuous casting tundish using analysis of RTD curves[J]. Journal of Iron and Steel Research, International , 2009, l6 (2) : 22–29. |
| [8] |
申小维, 包燕平, 李怡宏, 等.
板坯连铸双流73 t中间包控流装置优化的水模型研究[J]. 特殊钢 , 2013, 34 (6) : 18–21.
SHEN Xiaowei, BAO Yanping, LI Yihong, et al. A study of water model on optimizing flow control devices in 73 t tundish for two-strand slab casting[J]. Special Steel , 2013, 34 (6) : 18–21. (in Chinese) |
| [9] | DING Ning, BAO YanpingG, SUN Qisong, et al. Optimization of flow control devices in a single-strand slab continuous casting tundish[J]. International Journal of Minerals, Metallurgy and Materials , 2011, 18 (3) : 292–296. DOI:10.1007/s12613-011-0436-7 |
| [10] |
曹雄, 张胤, 贾攀, 等.
中间包结构优化的水模型正交试验[J]. 特殊钢 , 2009, 30 (4) : 39–41.
CAO Xiong, ZHANG Yin, JIA Pan, et al. Orthogonal test of water model for optimization of structure of tundish[J]. Special Steel , 2009, 30 (4) : 39–41. (in Chinese) |
| [11] | 李翼祺. 流体力学基础[M]. 北京: 科学出版社, 1974 . |
| [12] | Sahai Y, Ahuja R. Fluid dynamics of continuous casting tundishes physical modeling[J]. Ironmaking and Steelmaking , 1986, 13 (5) : 241–247. |
| [13] | Tanaka H, Tsujino R, Imamura A, et al. Effect of length of vertical section on inclusion removal in vertical bending-type continuous casting machine[J]. Journal of the Iron and Steel Institute of Japan International , 1994, 34 (6) : 498–506. DOI:10.2355/isijinternational.34.498 |
 2015, Vol. 38
2015, Vol. 38
