2. 鞍钢集团 钒钛(钢铁)研究院,四川 攀枝花 610031
2. Ansteel Research Institute of Vanadium & Titantium (Iron & Steel), Ansteel Corporation, Panzhihua, Sichuan 610031, P. R. China
液体金属凝固过程大多以枝晶形式生长,且枝晶生长过程中伴随着宏微观区域内溶质和温度变化,这将导致液体金属凝固成型过程产生由温度梯度和浓度梯度引起的自然对流。此外,很多液体金属凝固成型过程还存在电磁搅拌、超声振动等外力场作用所形成的强制对流。这些金属熔体流动行为将对枝晶生长形貌产生显著影响,进而影响金属成型凝固组织,成分偏析以及凝固疏松和缩孔等缺陷,并对最终金属凝固成型产品性能产生重要影响[1-3]。因此,对流作用下的枝晶生长行为研究对于控制金属凝固组织,生产高品质无缺陷金属产品至关重要。
数值模拟作为枝晶生长行为研究的有效手段,近些年发展尤为迅速。一些研究者[4-7]较早地采用相场模型(phase field)、耦合流场模型数值模拟了流场作用下的枝晶生长行为,定量分析了流动速度、方向和各向异性强度等因素对枝晶尖端生长速度、方向和枝晶形貌的影响。然而,由于相场模型对网格尺寸要求严格,使得相场模型计算效率较低,计算区域较小,且大多数数值模拟局限于纯物质和单枝晶生长。然而,元胞自动机方法(cellular automaton)基于随机捕获固液界面处相邻元胞,大大提高了计算效率,使得针对工业生产过程中金属凝固组织数值模拟成为可能。因此,元胞自动机方法受到越来越多关注。近些年,在微观尺度元胞自动机模型的基础上[8-10],国内外学者开始耦合Navier-Stokes方程的传统流体计算方法[11-15]或格子Boltzmann方法[16-19],研究了流场作用下枝晶生长规律。目前,元胞自动机模型能够较好地克服相场模型缺点,并成功地模拟了流场作用下多维多枝晶生长形貌。然而,大多数值模拟针对低熔点纯物质或者二元合金凝固过程枝晶生长的数值模拟,而钢凝固过程枝晶生长行为的研究则相对较少。
本研究将在笔者[20-21]前期开发的微观元胞自动机模型的基础上,耦合动量传输模型、质量传输模型和热量传输模型,建立宏微观多尺度二维枝晶生长数学模型CA-FVM[22]。进而研究强制对流对Fe-0.82C二元合金凝固过程枝晶生长的影响规律。
1 模型描述 1.1 宏观传输模型1)动量传输模型
常密度不可压缩流体流动满足连续性方程和Navier-Stokes方程。
连续性方程为
| $ \nabla \cdot u = 0。 $ | (1) |
Navier-Stokes方程为
| $ \rho \frac{{\partial u}}{{\partial t}} + \rho u \cdot \nabla u =-\nabla P + \nabla \cdot (\mu \nabla u), $ | (2) |
式中,u为速度矢量,ρ为密度,μ为黏度,P为压强。
2)质量传输模型
流场作用下的质量传输方程为
| $ \frac{{\partial C}}{{\partial t}} + \nabla \cdot (\xi uC) = \nabla \cdot (D\nabla C), $ | (3) |
式中,C为溶质浓度,D为溶质扩散系数,t为时间,ξ为元胞状态参数(当元胞为液体或界面时,ξ=1;当元胞为固体时,ξ=0)。
3)热量传输模型
流场作用下的热量传输方程为
| $ \frac{{\partial (\rho T)}}{{\partial t}} + \nabla \cdot (\rho uT) = \nabla \cdot (\frac{\lambda }{c}\nabla T) + \rho \frac{L}{c}\frac{{\partial {f_{\rm{s}}}}}{{\partial t}}, $ | (4) |
式中,T为温度,λ为导热系数,c为比热,L为潜热,fs为固相率。
1.2 微观枝晶生长模型1)枝晶尖端过冷度
凝固枝晶生长前沿过冷度ΔT可表示为
| $ \Delta T = \Delta {T_{\rm{c}}} + \Delta {T_{\rm{t}}} + \Delta {T_{\rm{k}}} + \Delta {T_{\rm{r}}}, $ | (5) |
式中, ΔTc、ΔTt、ΔTk和ΔTr分别为溶质过冷、热过冷、动力学过冷和曲率过冷。
由于动力学过冷只在非常高的凝固速率(快速凝固)下才对界面平衡温度产生影响,所以钢连铸凝固过程可以忽略动力学过冷的影响,只考虑热过冷、溶质过冷和曲率过冷对枝晶尖端过冷度的影响。因此,枝晶尖端过冷度可表示为
| $ \Delta T = \Delta {T_{\rm{t}}} + {m_0}(C_1^* - {C_0}) - \mathit{\Gamma }\kappa f(\varphi ,\theta ), $ | (6) |
式中, C0为合金初始浓度,Cl*为固液界面处液相溶质浓度,m0为液相线斜率,Г为Gibbs-Thomson系数,κ为平均固液界面曲率,f(φ, θ)为界面能各向异性函数,θ为枝晶择优生长角度,φ为固液界面法相与x轴的夹角。
2)界面曲率
固液界面曲率由界面处固相率梯度确定,为
| $ \kappa = \frac{{2{{({f_s})}_x}{{({f_s})}_y}{{({f_s})}_{xy}}- ({f_s})_x^2{{({f_s})}_{yy}}- ({f_s})_y^2{{({f_s})}_{xx}}}}{{{{[({f_s})_x^2 + ({f_s})_y^2]}^{\frac{3}{2}}}}}, $ | (7) |
界面张力的各向异性为
| $ f(\varphi, \theta ) = 1-15\varepsilon {\rm{cos}}(4(\varphi-\theta )), $ | (8) |
| $ \varphi = \arccos \left( {- \frac{{{{({f_{\rm{s}}})}_x}}}{{{{[({f_{\rm{s}}})_x^2 + ({f_{\rm{s}}})_y^2]}^{\frac{1}{2}}}}}} \right), $ | (9) |
式中, (fs)x和(fs)y为固相率的一阶偏导,(fs)xy,(fs)xy和(fs)yy为固相率的二阶偏导,ε为界面各向异性参数。
3)枝晶尖端生长速度
固液界面移动速度受界面处溶质浓度控制,为
| $ {v_{\rm{n}}}C_1^*(1-k) = {D_{\rm{s}}}\frac{{\partial {C_{\rm{s}}}}}{{\partial n}}{\left| {^*-{D_1}\frac{{\partial {C_1}}}{{\partial n}}} \right|^*}, $ | (10) |
式中:vn为界面法相移动速度,k为溶质平衡分配系数,Ds为溶质元素在固相中扩散系数,Dl为溶质元素在液相中扩散系数。
2 研究对象文中将研究强制对流对Fe-0.82C二元合金凝固过程柱状晶生长规律的影响。模型计算所涉及的物性参数见表 1所示。
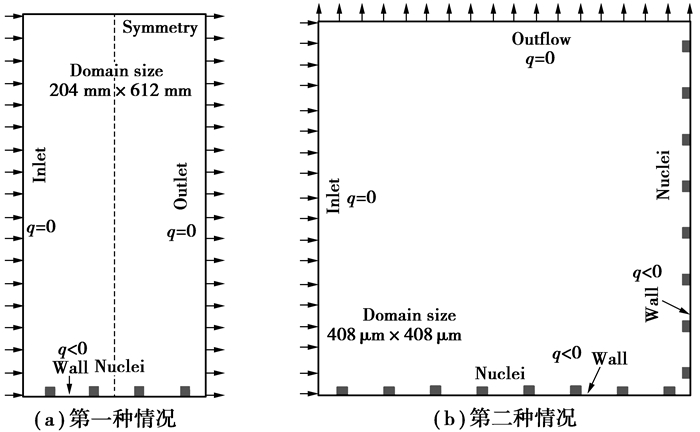
分别设计了两种不同流动方式和柱状晶生长方式来研究强制对流对柱状晶生长规律的影响。第一种情况(图 1(a)),4个形核质点位于204 μm×612 μm计算区域底部,各形核质点间距离51 μm,热量从计算区域底部传出,其余边界为绝热边界条件。流体从计算区域左边流入,右边流出,底部为壁面边界条件,顶部为对称边界条件。第二种情况(图 1(b)),计算区域为408 μm×408 μm,计算区域底部和右边分别等距离分布8个形核质点,热量从计算区域底部和右边传出,其余两边为绝热边界条件。流体从计算区域左边流入,顶部流出,其余两边为壁面边界条件。
|
图 1 计算实例示意图 Figure 1 Schematic diagram of two numerical cases |
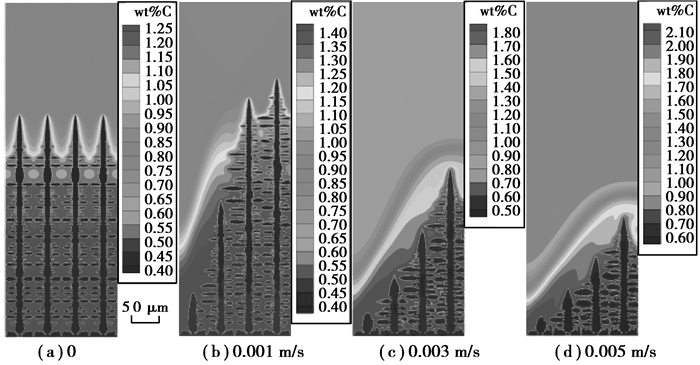
图 2为计算区域底部热通量2.0 MW/m2时,左侧入口速度从0增加到0.005 m/s对柱状晶形貌和溶质分布的影响。从图中可以看出,在没有流动的定向凝固情况下,从计算区域底部形核的柱状晶径直向熔体内部生长,并将溶质元素向固液界面前沿排除。由于溶质元素在熔体中的扩散较慢,因此,随着柱状晶继续生长,柱状晶根部将会富集大量的溶质元素,形成枝晶间溶质偏析,这就是常说的溶质微观偏析。同时,一次枝晶臂表面溶质元素富集将会造成固液界面失衡,从而形成二次枝晶臂。此外,没有流动影响的柱状晶形貌完全一样,这是由于这4个人为设置的柱状晶生长位置相对较远,彼此将不存在竞争生长和相互影响,都能够充分生长。当熔体中存在强制对流时,计算区域内溶质分布发生明显的变化,枝晶生长存在严重的不对称,计算区域底部生长的枝晶形貌相差甚远。当左侧入口流速为0.001 m/s时,左侧入口强制对流促使左侧枝晶根部富集的溶质元素翻越生长的枝晶障碍逐渐向右侧出口迁移,使得高浓度溶质区波及靠近左侧生长的两个柱状晶,枝晶生长受到明显的抑制作用,枝晶生长较慢。然而靠近右侧出口的两个枝晶则生长较快,这是由于枝晶生长前沿富集的溶质在强制对流的作用下被带走,从而使得枝晶尖端溶质浓度梯度较大,枝晶生长受到明显的促进作用。随着左侧入口流速的增加,强制对流对溶质分布和枝晶生长的影响增加,枝晶形貌发生明显变化。当强制对流速度大于0.003 m/s时,强制对流引发的溶质高浓度区完全覆盖底部生长的4个柱状晶,柱状晶生长受到抑制。强制对流速度越大,枝晶生长抑制作用越强,且越靠近强制对流入口位置处枝晶受影响越大。同时,固液界面处富集的溶质元素被强制对流带走,柱状晶迎流侧不容易产生二次枝晶臂。
|
图 2 在相同底部热通量2.0 MW/m2和不同流体速度情况下生长200 ms后柱状晶形貌 Figure 2 Columnar dendrites after 200 ms under heat flux of 2.0 MW/m2 with different inlet velocities |
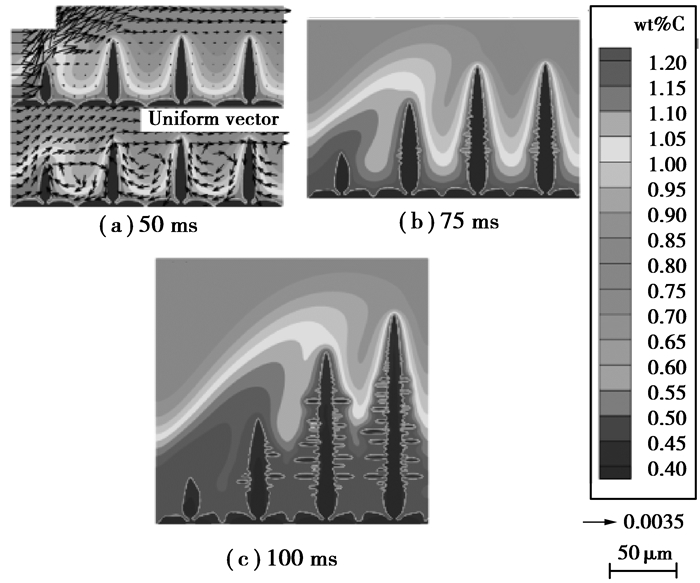
图 3是计算区域底部热通量,为1.5 MW/m2,左侧入口流速0.003 m/s时,柱状晶生长变化。为清晰地显示计算区域内流场,水平和竖直方向每隔8个节点画一个矢量。从图中可以看出,从左侧流入的流体将会翻越底部向熔体中心生长的柱状晶障碍,然后从计算区域右侧流出,并在柱状晶之间形成漩涡。同时,在强制对流的作用下,枝晶间富集的溶质元素逐渐向出口方向迁移,从而使得底部生长的柱状晶受高浓度溶质元素区迁徙的影响。因此,随着时间的推移,底部生长的柱状晶从左到右,依次受到抑制,且抑制程度逐渐减轻,枝晶生长速度逐渐增加。同时,远离强制对流入口处枝晶生长更加充分,能够观察到明显的二次枝晶臂的产生。
|
图 3 热通量和入口速度分别为1.5 MW/m2和0.003 m/s时,不同时间下柱状晶形貌 Figure 3 Morphology of columnar dendrites with heat flux of 1.5 MW/m2 and inlet velocity of 0.003 m/s after 50 ms, 75 ms and 100 ms |
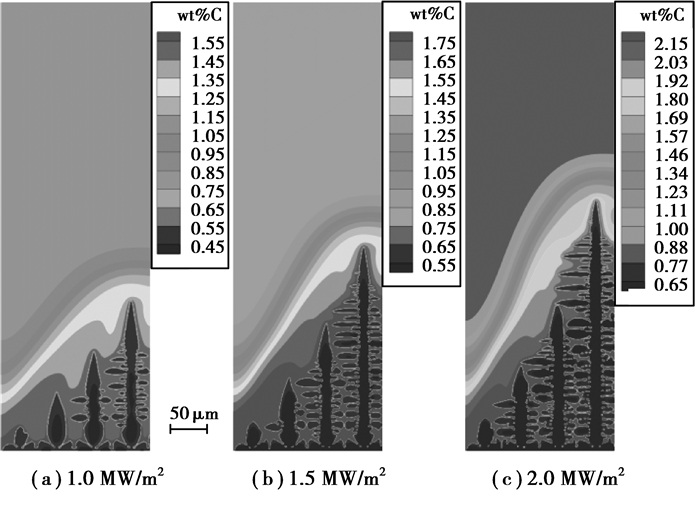
图 4为计算区域左侧入口流速0.003 m/s,底部热通量分别为1.0、1.5和2.0 MW/m2时,250 ms后枝晶形貌。从图中可以看出,随着冷却强度的增加,枝晶生长速率增加。相同生长时间条件下,冷却强度越大,枝晶生长越粗大,枝晶间二次枝晶臂发展越充分,枝晶间溶质富集越严重。此外,不同冷却强度条件下,底部生长的柱状晶从左到右,受强制对流影响的程度依次减轻,枝晶生长速度增加。且冷却强度越大,靠近强制对流入口处枝晶生长受抑制影响越大,远离强制对流入口处枝晶生长受抑制越小。
|
图 4 在相同入口流速0.003 m/s和不同冷却强度下,柱状晶生长250 ms后形貌 Figure 4 Morphology of columnar dendrites after 250 ms with inlet velocity of 0.003 m/s under different heat fluxes |
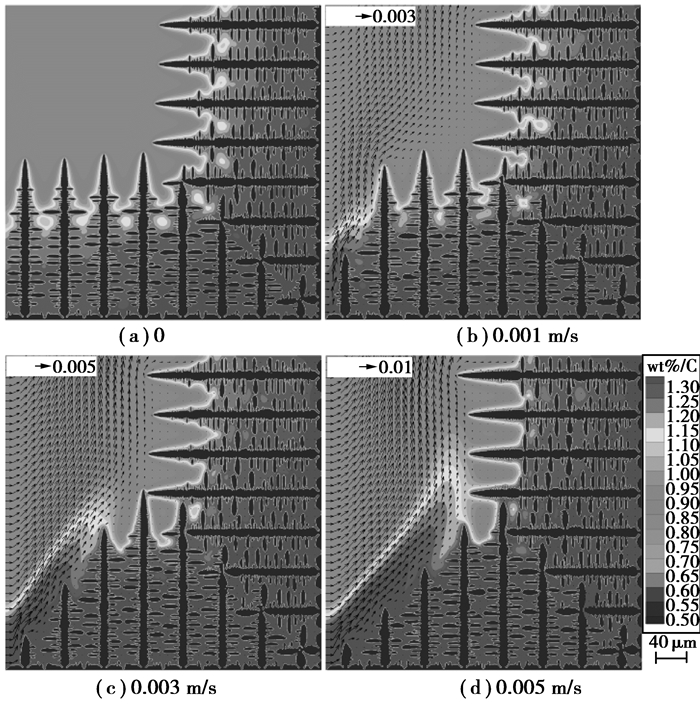
图 5为第二种计算情况下,底部和右侧热通量为1.5 MW/m2,强制对流速度从0增加到0.005 m/s,枝晶生长100 ms后的形貌。同时,为了清晰地显示计算区域内流场,水平和竖直方向每隔10个节点画一个矢量。从图中可以看出,在无熔体流动状态下,计算区域底部和右侧的枝晶均垂直于区域边界,沿热流相反方向朝熔体中心生长。底部和右侧生长的柱状晶在正方形计算区域对角线处相遇,然后停止生长。同时,枝晶生长过程中排除的溶质元素富集在枝晶干根部,在枝晶间形成富含溶质区域。生长过程中排除的溶质元素富集在枝晶臂表面,使得固液界面失衡,产生二次枝晶臂。最终,计算区域内形成沿左斜对角线对称分布的枝晶形貌和溶质分布图。当强制对流存在时,强制对流从计算区域左侧进入,顶部离开,枝晶臂间形成涡流。枝晶生长过程中排除的溶质元素在强制对流的作用下向出口迁徙,从而在靠近强制对流入口处枝晶生长前沿形成高浓度溶质区域,抑制柱状晶生长。然而,在靠近流体出口处,枝晶生长前沿排除的溶质元素被强制对流带走,枝晶生长前沿生长速率增加。随着强制对流速度的增加,流体入口处高浓度溶质区域扩大,受抑制的柱状晶数量增加。同时,靠近流体出口处枝晶生长速率明显增加。
|
图 5 在相同热通量1.5 MW/m2和不同流体入口速度情况下,枝晶生长100 ms后形貌 Figure 5 Morphology of columnar dendrites after 100 ms with heat flux of 1.5 MW/m2 and different inlet velocities |
1) 在微观元胞自动机模型的基础上,建立了考虑动量传输、质量传输和热量传输的宏微观多尺度二维枝晶生长数学模型CA-FVM。
2) 采用CA-FVM研究了Fe-0.82C二元合金凝固过程强制对流对柱状晶生长规律的影响。数值模拟表明:强制对流能够明显地改变枝晶生长规律,靠近强制对流入口处枝晶生长受抑制作用较明显,远离强制对流入口处枝晶受抑制作用较弱。同时,随着对流强度的增加,枝晶生长受熔体流动的影响更加明显,加剧了枝晶的非对称生长。
| [1] | Stefanescu D. Science and engineering of casting solidification[M]. New York: Springer, 2009 . |
| [2] | 李依依, 李殿中, 朱苗勇. 金属材料制备工艺的计算机模拟[M]. 北京: 科学出版社, 2006 . |
| [3] |
王怀志, 张殿喜, 王智平, 等.
对流对枝晶生长影响的数值模拟研究进展[J]. 材料导报 , 2009, 23 (14) : 237–240.
Wang H Z, Zhang D X, Wang Z P, et al. Process in numerical simulation for convection on dendritic growth[J]. Material Review , 2009, 23 (14) : 237–240. (in Chinese) |
| [4] | Beckermann C, Diepers H J, Steinbach I, et al. Modeling melt convection in phase-field simulations of solidification[J]. Journal of Computational Physics , 1999, 154 (2) : 468–496. DOI:10.1006/jcph.1999.6323 |
| [5] | Tong X, Beckermann C, Karma A, et al. Phase-field simulations of dendritic crystal growth in forced flow[J]. Physical Review E , 2001, 63 (6) : 061601. |
| [6] | Lan C W, Hsu C M, Liu C C. Efficient adaptive phase field simulation of dendritic growth in a forced flow at low supercooling[J]. Journal of Crystal Growth , 2002, 241 (3) : 379–386. DOI:10.1016/S0022-0248(02)01287-3 |
| [7] | Natsume Y, Ohsasa K, Narita T. Investigation of the mechanism of alloy dendrite deflection due to flowing melt by phase-field simulation[J]. Materials Transaction , 2002, 43 (9) : 2228–2234. DOI:10.2320/matertrans.43.2228 |
| [8] | Nastac L. Numerical modeling of solidification morphologies and segregation patterns in cast dendritic alloys[J]. Acta Materialia , 47 (17) : 4253–4262. DOI:10.1016/S1359-6454(99)00325-0 |
| [9] | Zhu M F, Hong C P. A modified cellular automaton model for the simulation of dendritic growth in solidification of alloys[J]. ISIJ International , 2001, 41 (5) : 436–445. DOI:10.2355/isijinternational.41.436 |
| [10] | Eshraghi M, Felicelli S D, Jelinek B. Three dimensional simulation of solute dendrite growth using lattice Boltzmann and cellular automaton methods[J]. Journal of Crystal Growth , 2012, 354 (1) : 129–134. DOI:10.1016/j.jcrysgro.2012.06.002 |
| [11] | Yuan L, Lee P D, Djambazov G, et al. Numerical simulation of the effect of fluid flow on solute distribution and dendritic morphology[J]. International Journal of Cast Metals Research , 2009, 22 (1-4) : 204–209. DOI:10.1179/136404609X368136 |
| [12] | Yuan L, Lee P D. Dendritic solidification under natural and forced convection in binary alloys: 2D versus 3D simulation[J]. Modelling and Simulation in Materials Science and Engineering , 2010, 18 (5) : 055008. DOI:10.1088/0965-0393/18/5/055008 |
| [13] | Shin Y H, Hong C P. Modeling of dendritic growth with convection using a modified cellular automaton model with a diffuse interface[J]. ISIJ International , 2002, 42 (4) : 359–367. DOI:10.2355/isijinternational.42.359 |
| [14] | Li D M, Li R, Zhang P W. A cellular automaton technique for modeling of a binary dendritic growth with convection[J]. Applied mathematical modelling , 2007, 31 (6) : 971–982. DOI:10.1016/j.apm.2006.04.004 |
| [15] |
朱鸣芳, 戴挺, 李成允, 等.
对流作用下枝晶生长行为的数值模拟[J]. 中国科学: E辑 , 2005, 35 (7) : 673–688.
ZHU Mingfang, DAI Ting, LI Chengyun, et al. Numerical modeling of dendritic growth in the presence of convection[J]. Science in China: Series E , 2005, 35 (7) : 673–688. (in Chinese) |
| [16] |
杨朝蓉, 孙东科, 潘诗琰, 等.
CA-LBM模型模拟自然对流作用下的枝晶生长[J]. 金属学报 , 2009, 45 (1) : 43–50.
YANG Chaorong, SUN Dongke, PAN Shiyan Y, et al. CA-LBM model for the simulation of dendritic growth under natural convection[J]. Acta Metallugica Sinica , 2009, 45 (1) : 43–50. (in Chinese) |
| [17] | Sun D K, Zhu M F, Pan S, et al. Lattice Boltzmann modeling of dendritic growth in a forced melt convection[J]. Acta Materialia , 2009, 57 (6) : 1755–1767. DOI:10.1016/j.actamat.2008.12.019 |
| [18] | Sun D K, Zhu M F, Pan S, et al. Lattice Boltzmann modeling of dendritic growth in forced and natural convection[J]. Computers & Mathematics with Applications , 2011, 61 (12) : 3585–3592. |
| [19] | Yin H, Felicelli S D, Wang L. Simulation of dendritic microstructure with lattice Boltzmann and cellular automaton methods[J]. Acta Materialia , 2011, 59 (8) : 3124–3136. DOI:10.1016/j.actamat.2011.01.052 |
| [20] | Luo S, Zhu M Y, Louhenkilpi S. Numerical simulation of solidification structure of high carbon steel in continuous casting using cellular automaton method[J]. ISIJ International , 2011, 52 (5) : 823–830. |
| [21] | Luo S, Zhu M Y. A two-dimensional model for the quantitative simulation of the dendritic growth with cellular automaton method[J]. Computational Materials Science , 2013, 71 : 10–18. DOI:10.1016/j.commatsci.2012.12.040 |
| [22] | Wang W L, Luo S, Zhu M Y. Dendritic growth of high carbon iron-based alloy under constrained melt flow[J]. Computational Materials Science , 2014, 95 : 136–148. DOI:10.1016/j.commatsci.2014.07.017 |
 2015, Vol. 38
2015, Vol. 38

