随着环境友好型设计理念、方法及技术的不断发展,水润滑橡胶轴承因其以水作为润滑介质而具有良好润滑特性及环境友好性,得到越来越广泛的应用[1]。已有文献对水润滑橡胶合金轴承的摩擦学性能、润滑性能等方面进行了大量研究[2-6]。但是,水润滑橡胶合金, 轴承在低速、重载等不良工况下易出现异常振动而产生高频尖叫噪声[7],影响了船舶的性能及安全性,因此,对水润滑橡胶合金轴承摩擦噪声的研究成为了近年来的研究热点之一。国内外学者的研究表明,水润滑橡胶轴承在低速重载下的摩擦噪声特征与轴轴承组成的摩擦系统密切相关[8-10],而水润滑橡胶轴承摩擦系统与轴承材料[11]、轴承结构[12]、工作温度[13]、负荷[14]等多种因素有关,尤其是不同的结构参数对轴承的润滑和摩擦特性有直接的关系,因此,研究水润滑橡胶合金轴承的结构参数对其摩擦噪声的影响具有较大的意义。
笔者应用有限元分析方法对一定摩擦条件下水润滑轴承进行复模态分析,重点分析不同结构参数对其摩擦振动噪声的影响,并对其进行实验验证,为低噪声水润滑轴承设计提供理论依据。
1 计算理论和分析模型 1.1 摩擦噪声复模态分析理论水润滑橡胶合金轴承系统的动力学方程[5]可以写为
| $ \boldsymbol{M\ddot{X}}+\boldsymbol{C\dot{X}}+(\boldsymbol{K}-{{\boldsymbol{K}}_{f}})\boldsymbol{X}=0, $ | (1) |
式中:M、C、K分别为轴承系统的质量矩阵、阻尼矩阵和刚度矩阵;Kf是橡胶轴承和轴之间的摩擦而引入的非对称刚度矩阵,这个非对称的刚度矩阵耦合了两者之间的法向相对位移和切向力;X为位移向量。从矩阵的角度来说,当不对称矩阵满足一定的条件,其特征值及特征向量就会是复数。那么运动方程可被改写成
| $ ({{\mu }^{2}}\boldsymbol{M}+\mu \boldsymbol{C}+\boldsymbol{K}+{{\boldsymbol{K}}_{f}})\boldsymbol{\varphi} =0, $ | (2) |
式中:μ为特征值; φ为特征向量,特征值和特征向量都有可能是复数。从物理意义上看,刚度矩阵的不对称达到一定的程度时,就可能导致系统内部的能量馈入,使得系统成为一个发散系统。而从数学角度来看,当刚度矩阵是一个非对称矩阵时,就意味着特征矩阵是不对称的,而不对称矩阵在一定条件下,其特征根及其特征向量是复数,即系统的其各阶模态频率和模态振型都是复数。
假设第n阶模态频率是λn=αn+iβn,虚部βn反映的是系统振动时的固有频率,而实部αn反映的是系统的稳定性。如果αn为正,就说明第n阶模态的阻尼比是负数,系统振动时其振幅会随着时间的增加变得越来越大,就会导致系统运动失稳,这样的模态被称为不稳定模态。若模态不稳定,则轴承系统就会可能产生振动噪声。因此,文中利用有限元分析软件对轴承系统进行复模态分析,依据复特征值实部的正负判断轴承系统发生噪声的可能性, 如果有实部为正的特征值, 则可判断系统有发生噪声的可能性。
1.2 有限元模型研究对象为某型水润滑橡胶合金轴承,其相关几何参数与材料参数如表 1、表 2所示。
| 表 1 轴承系统各部件的几何参数 Table 1 The geometrical parqments of bearing |
| 表 2 轴承系统各部件的材料参数 Table 2 The material paraments of bearing |
对于橡胶类物理非线性材料,常用Mooney-Rivlin模型来描述[15]为
| $ W({{I}_{1}}, {{I}_{2}})={{\sum\limits_{i, j}{{{C}_{ij}}({{I}_{1}}-3)}}^{i}}{{({{I}_{2}}-3)}^{j}}, $ | (3) |
式中:W(I1,I2)为应变能函数;Cij为Rivlin系数; I1和I2为第1、第2 Green应变不变量。文中采用两参数模型。则公式(3)转化为
| $ W = {C_{01}}({I_1} - 3) + {C_{10}}({I_2} - 3), $ | (4) |
式中:C10=0.969 6 MPa,C01=0.129 MPa。
根据轴承结构建立了图 1所示的轴承系统的有限元模型,在建模过程中,根据实际情况,对轴承系统做了如下简化:

|
图 1 水润滑橡胶合金轴承系统有限元模型 Figure 1 Finite element model of bearing system |
1) 在实际情况下,铜套和橡胶内圈都是固定约束的,为了提高计算速度,可以省去铜套部分;
2) 将轴承系统的主轴简化为一刚性轴,长度大约为轴承的9倍。
1.3 边界条件在实际工况下,轴的硬度远大于轴承橡胶的硬度,因此, 将轴设为刚体。在水润滑橡胶轴承的复特征值求解过程中,边界条件设置为:1)轴的右端径向和轴向固定,即约束轴的x、y、z 3个方向上的平移自由度和x、y 2个方向上的转动自由度;2)轴承橡胶完全固定,即约束轴承的所有自由度;3)载荷以力的形式施加在左端面上,方向为X轴负向,如图 2所示。

|
图 2 水润滑橡胶轴承系统的载荷与约束 Figure 2 Load and boundary condition of bearing system |
针对上述平板型水润滑橡胶轴承系统模型,研究了不同轴承系统的结构参数(水槽半径、水槽型式及摩擦面形状)在不同摩擦系数条件下对摩擦振动噪声的影响。
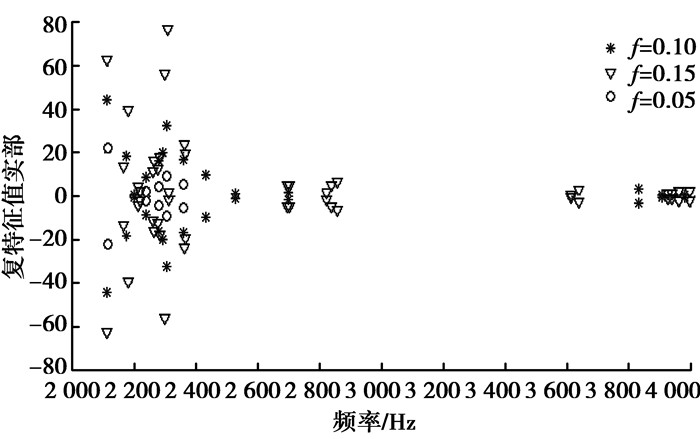
2.1 摩擦系数对摩擦噪声的影响分析首先研究摩擦系数对振动噪声的影响,根据试验数据[11],复特征值分析可提取到4 000 Hz。在偏载力1 000 N,轴承转速5 rad/s的情况下,分别取摩擦系数f=0.05、0.10、0.15,计算轴承系统的复模态分布如图 3所示。图 3显示了3种不同摩擦系数下产生振动噪声的预测结果,计算结果表明,当f=0.05时,有5个不稳定模态,在频率为2 115 Hz时,出现最大的特征值实部22.22。当f=0.15时,有25个不稳定模态,在频率为2 310 Hz时,出现最大的特征值实部76.43,即在这些频率下轴承系统极易产生振动噪声。图中还表明,摩擦系数越大,不稳定模态也越多,复特征值正实部的数值也增大,系统发生不稳定的趋势增大,即轴承系统发生尖叫噪声的趋势会随着摩擦系数的增加而增大,说明较大的摩擦系数更易导致系统相邻的模态发生耦合,从而增大了产生摩擦噪声的可能性。有关试验也表明,摩擦系数对振动噪声有非常重要的影响,摩擦系数越大越容易出现噪声。
|
图 3 不同摩擦系数的复模态分布图 Figure 3 The complex model distribution of friction-coefficient |
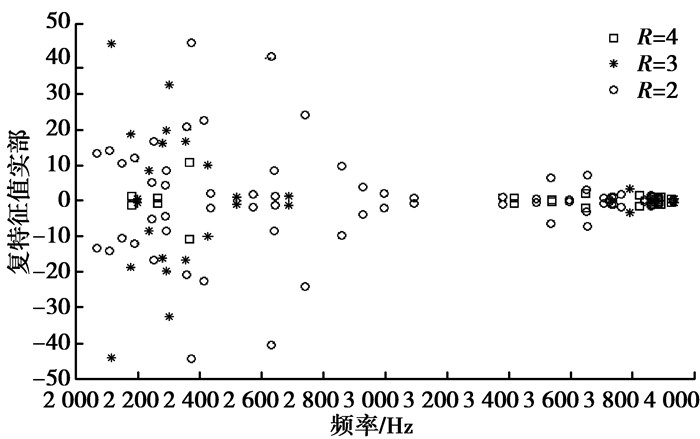
在其他条件相同的情况下,分析橡胶轴承水槽半径大小对橡胶轴承系统的稳定性及产生摩擦噪声概率的影响,分别取水槽半径R=4、3、2 mm,计算不同水槽半径的复特征值分布情况,计算时,取f=0.10,偏载为1 000 N,轴转速为5 rad/s。计算结果如图 4所示。
|
图 4 不同水槽半径的复模态分布图 Figure 4 The complex modal distribution of groove radius |
图 4显示,在2 000~4 000 Hz内,当水槽半径R为2时,系统不稳定模态有37个,耦合模态实部最大值出现在2 379 Hz,其值为45;当R为3时,有14个不稳定模态,耦合模态实部最大值出现在2 114 Hz,其值为44.12;当R为4时,有12个不稳定模态,耦合模态实部最大值出现在2 372 Hz,其值为10.7,远远少于半径较小的水槽,且失稳倾向也普遍要比半径较小的水槽要小,由此可以说明摩擦噪声受水槽半径大小的影响很大,水槽半径越大,不稳定模态的个数和复特征值实部不断减小,随着水槽半径的增加,轴承系统出现噪声的概率会有明显的下降趋势。采用较大的水槽半径会减少接触摩擦面的面积,从而有利于减小摩擦噪声出现的概率。优化设计时,在结构合理的情况下,为了减小轴承系统的摩擦噪声,尽可能地增大水道槽的半径。
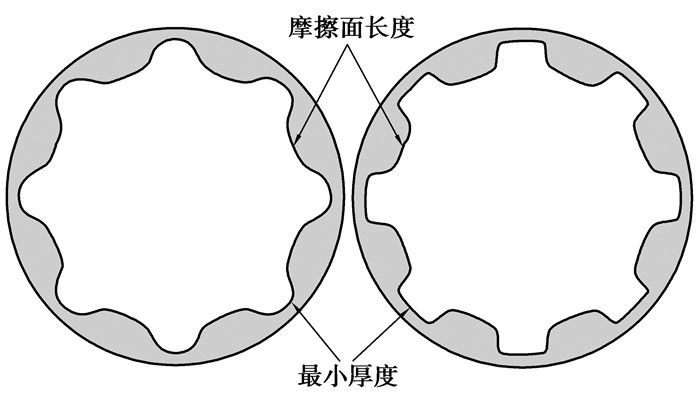
2.3 水槽型式对摩擦噪声的影响水润滑轴承水槽型式取圆弧形水槽和梯形水槽,为保证其分析结果的可比性,在结构上保持摩擦面的长度基本相同及橡胶的最小厚度基本相同,如图 5所示。计算时,取f=0.10,偏载为1 000 N,轴转速为5 rad/s。计算结果如图 6所示。
|
图 5 不同水槽示意图 Figure 5 Schematic diagram of different groove types |
|
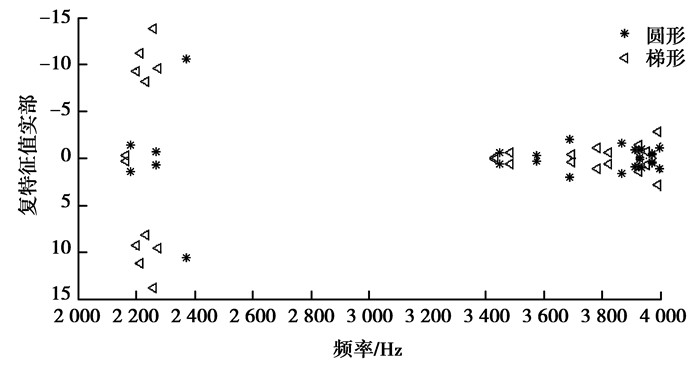
图 6 2种水槽的复模态分布图 Figure 6 The complex modal distribution of two groove types |
图 6表明,当水槽为圆弧形时,轴承系统的不稳定模态个数为12个,耦合模态实部最大值出现在2 372 Hz,其值为10.7;而水槽为梯形时则为14个,耦合模态实部最大值出现在2 259 Hz,其值为13.8,这说明水槽结构型式对摩擦振动噪声的影响不大。
2.4 摩擦面形状对摩擦噪声的影响为研究摩擦面形状对摩擦噪声的影响,取平板形和圆弧形摩擦面进行分析,分析条件取f=0.10,偏载1 000 N,轴转速5 rad/s。,计算结果如图 7所示。
|
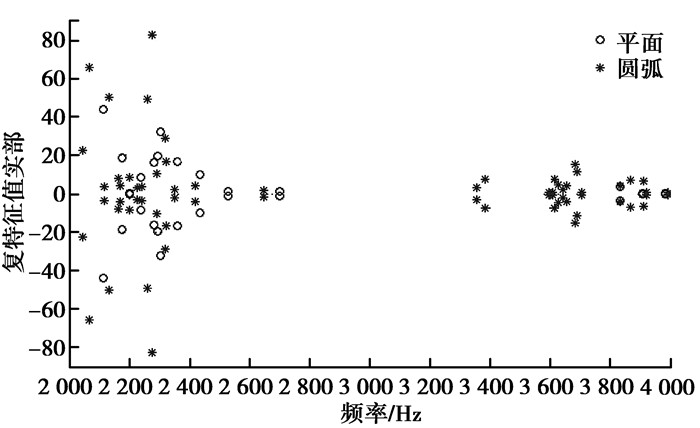
图 7 2种摩擦面的复模态分布图 Figure 7 The complex model distribution of two friction sruface |
计算结果表明,当摩擦面为平面时,轴承系统的不稳定模态为14个,耦合模态实部最大值出现在2 114 Hz,其值为41.72;当摩擦面为圆弧时,轴承系统有32个不稳定模态,耦合模态实部最大值出现在2 276 Hz,其值为82.72。此外,圆弧形摩擦面的复特征值正实部普遍要比平面形的要大,即圆弧形的失稳倾向要大些,产生噪声的可能性要大。分析其原因,圆弧形摩擦面较平面形摩擦面来说,其有效接触面积要大些,从而增加了出现摩擦噪声的可能性。
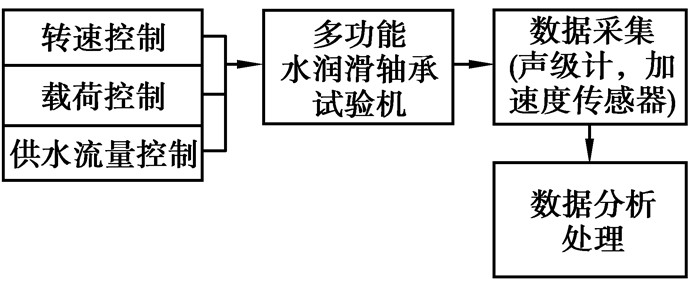
3 实验研究图 8为水润滑橡胶合金轴承摩擦噪声实验系统框图。为比较2种轴承结构对摩擦噪声的敏感度,在此实验装置上对平板型和圆弧型水润滑橡胶轴承进行了一定载荷下摩擦系数实验和噪声实验。摩擦噪声实验过程是在一定载荷和润滑水流量下,改变主轴转速大小,到轴承首次出现摩擦噪声,记录此时的主轴速度及噪声信号(该主轴转速称为某一轴承在一定条件下出现噪声的临界转速)。
|
图 8 实验系统框图 Figure 8 Experimental system diagram |
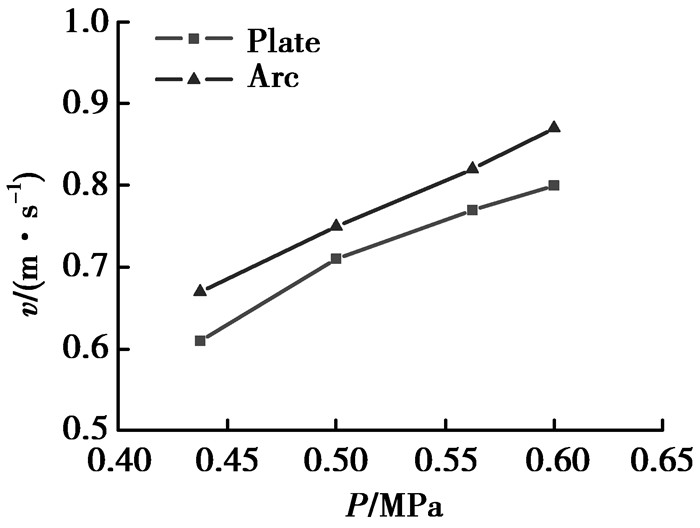
图 9是2种平板型和圆弧型结构轴承在不同比压(主轴载荷)下的临界转速(润滑水流量为0.171 L/min)。
|
图 9 2种轴承临界速度对比图 Figure 9 The comparison chart on critical speed two types bearing |
从图 9可以看出,随着轴承比压的不断上升,橡胶轴承的临界速度不断变大,橡胶轴承的变形变大,摩擦面接触面积变大,会使得摩擦系数变大,从而导致临界速度上升。通过比较也可以得出,在相同载荷下,平板型橡胶轴承的临界速度要比圆弧型橡胶轴承的临界速度要小,因此,在抑振降噪性能方面来说,平板型橡胶轴承的性能要优于圆弧型橡胶轴承,这与分析结果是吻合的。
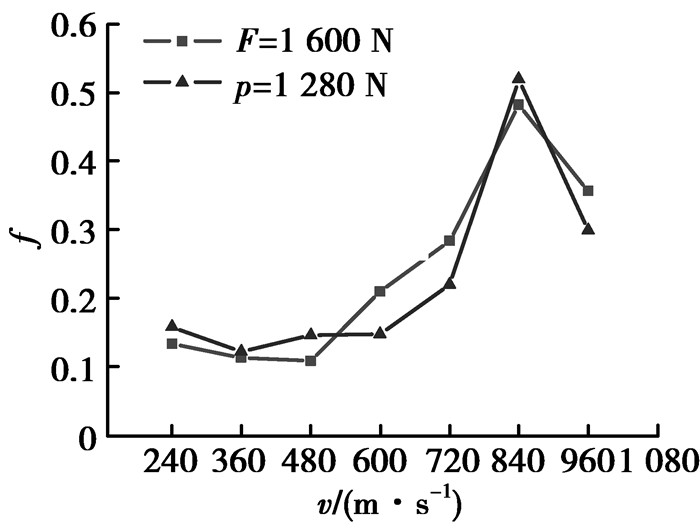
此外,对产生噪声时的摩擦系数记录结果也表明,发生噪声时系统摩擦系数急剧增大。如图 10所示,在一定的载荷下,当转速增大时,摩擦系数由0.15急剧增大到0.5,在720~960 r/min范围内都记录到了轴承生产的噪声,这与分析结果也是吻合的。
|
图 10 摩擦系数变化曲线 Figure 10 The curve of friction-coefficient |
水润滑橡胶合金轴承摩擦噪声的复模态分析和实验研究表明,水润滑橡胶合金轴承中水槽半径大小、摩擦面形状及橡胶摩擦副间的摩擦系数对水润滑轴承的摩擦噪声产生的概率有较大影响。因此,设计半径较大的水槽、摩擦面为平面形的结构,以及选择摩擦系数较小的摩擦副材料都可以减少轴承系统产生摩擦噪声的可能性。计算结果还表明,水槽的形状对轴承摩擦噪声的产生概率影响不大。
| [1] |
王优强, 杨成仁.
水润滑橡胶轴承研究进展[J]. 润滑与密封, 2001(2): 65–67.
WANG Youqiang, YANG Chengren. The development and study of the water-lubricated rubber bearings[J]. Lubrication Engineering, 2001(2): 65–67. (in Chinese) |
| [2] |
周广武, 王家序, 李俊阳, 等.
螺旋槽水润滑橡胶合金轴承摩擦学性能实验[J]. 重庆大学学报:自然科学版, 2013, 36(3): 1–5.
ZHOU Guangwu, WANG Jiaxu, LI Junyang, et al. Experimental investigation of tribological properties for spiral groove water lubricated rubber bearings[J]. Journal of Chongqing University:Natural Science Edition, 2013, 36(3): 1–5. (in Chinese) |
| [3] |
孟凡明.
水润滑轴承系统三维热弹流性能有限元分析[J]. 重庆大学学报:自然科学版, 2013, 36(2): 121–126.
MENG Fanming. Three-dimensional finite element analysis for thermo-elasto-hydrodynamic performances for a water lubricated bearing system[J]. Journal of Chongqing University:Natural Science Edition, 2013, 36(2): 121–126. (in Chinese) |
| [4] |
田宇忠, 刘正林, 刘宇, 等.
带轴向槽水润滑轴承润滑性能数值分析与研究[J]. 船海工程, 2009, 38(3): 56–59.
TIAN Yuzhong, LIU Zhenglin, LIU Yu, et al. Numerical calculation and study on lubrication performance of water-lubricated bearings with axial groove[J]. Ship & Ocean Engineering, 2009, 38(3): 56–59. (in Chinese) |
| [5] |
王优强, 王龙, 黄丙习, 等.
水润滑橡胶轴承摩擦试验研究[J]. 农业机械学报, 2006, 37(2): 136–140.
WANG Youqiang, WANG Long, HUANG Binxi, et al. Experimental study on friction and wear mechanism between rubber/nickel coating on steel[J]. Transactions of Chinese Society for Agricultural Machinery, 2006, 37(2): 136–140. (in Chinese) |
| [6] |
姚世卫, 王娟, 王隽, 等.
水润滑橡胶轴承磨擦行为及试验研究船舶科学技术[J]. 船舶科学技术, 2009, 31(12): 32–35.
YAO Shiwei, WANG Juan, WANG Jun, et al. Vibration and noise generation theory and experiment of water-lubricated rubber bearings[J]. Ship Science and Technology, 2009, 31(12): 32–35. (in Chinese) |
| [7] |
姚世卫, 胡宗成, 马斌, 等.
橡胶轴承研究进展及在舰艇上的应用分析[J]. 舰船科学技术, 2005, 27(S1): 27–31.
YAO Shiwei, HU Zongcheng, MA Bin, et al. The new development of rubber bearing and its application in warships[J]. Ship Science and Technology, 2005, 27(S1): 27–31. (in Chinese) |
| [8] |
秦红玲, 周新聪, 闫志敏, 等.
水润滑尾轴承振鸣音研究进展[J]. 噪声与振动控制, 2013(1): 123–127.
QIN Hongling, ZHOU Xincong, YAN Zhimin, et al. Review of Research Advances of Water-lubricated Stern Bearing Noise[J]. Noise and Vibration Control, 2013(1): 123–127. (in Chinese) |
| [9] | Ibrahim R A. Friction-induced vibration, chatter, squeal, and chaos-part I:Mechanics of contact and friction[J]. Applied Mechanics Reviews, 1994, 47(7): 209–226. DOI:10.1115/1.3111079 |
| [10] | Ibrahim R A. Friction-induced vibration, chatter, squeal, and chaos-part Ⅱ:dynamics and modeling[J]. Applied Mechanics Reviews, 1994, 47(7): 227–253. DOI:10.1115/1.3111080 |
| [11] |
周新聪, 闫志敏, 唐育民, 等.
低噪声舰船尾管水润滑橡胶轴承材料的研究[J]. 中国造船, 2013, 54(2): 77–85.
ZHOU Xincong, YAN Zhimin, TANG Yumin, et al. Study of low noise water lubrication rubber bearing material SPB-N for ship stern tube[J]. Ship Building of China, 2013, 54(2): 77–85. (in Chinese) |
| [12] |
陈战.水润滑轴承的摩擦磨损性能及润滑机理的研究[D].重庆:重庆大学, 2003. CHEN Zhan.Study on Friction and Wear Property and Lubricant Mechanism of Water Lubricated Bearing[D].Chongqing:Chongqing University, 2003. |
| [13] |
戴燕.基于FLUENT的水润滑尾轴承冷却润滑性能研究[D].武汉:武汉理工大学, 2012. DAI Yan.Influence of Water-lubricated Rubber Stern Tube Bearings[D].Wuhan:Wuhan university of technology, 2012. |
| [14] | Pai R S, Pai R, Hargreaves D J.In static and dynamic characteristics of a 3-axial groove water lubricated journal bearing[C]//4th International Conference on Tribology for Equipment Reliability ICIT, Mumbai, 2004, 15-18:355-361. |
| [15] |
王伟, 邓涛, 赵树高.
橡胶Mooney-Rivlin模型中材料常数的确定[J]. 特种橡胶制品, 2004, 25(4): 30–33.
WANG Wei, DENG Tao, ZHAO Shugao. Determination for material constants of rubber Mooney-Rivlin model[J]. Special Purpose Rubber Products, 2004, 25(4): 30–33. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38

