2. 重庆华冶钢结构技术研究院,重庆 401147
2. Chongqing Huaye Institute of Steel Structural Technology, Chongqing 401147, P.R.China
近年来,人们越来越多地观察到钢构件在高温下的局部失稳现象,高温局部稳定问题也越来越受到科研人员的关注[1-2]。Feng等[3-5]对冷成型薄壁构件做了大量的试验和有限元分析,提出了这类构件高温下的局部稳定计算方法。Bradford等[6-7]采用半解析的有限条分法分析了组合梁受压翼缘和腹板的局部稳定性能,提出了相应的翼缘宽厚比和腹板高厚比限值。Knobloch和Fontana[8]在有限元分析的基础上提出了基于应变的钢构件高温下局部稳定计算方法。但该方法没有经过试验结果的验证,计算公式也比较复杂,工程上使用起来不方便。美国规范[9]则是沿用常温下的局部稳定理论,直接代入高温下的材性计算局部稳定性能。EC3[10]除了考虑高温下的材性之外,还引入了0.85的折减系数,以考虑材料非线性的影响。以上规范对钢构件高温下的局部稳定问题处理都相对粗略,而中国《钢结构设计规范》[11]和《建筑钢结构防火技术规范》[12]则没有这方面的条文及说明。
在文献[13]的试验基础上,采用经验证的Abaqus有限元模型,分析了温度、宽厚比、翼缘和腹板相互作用以及初始几何缺陷等因素对H形截面构件局部稳定性能的影响,采用数值分析方法拟合出Q235和Q460钢H形截面高温下的局部稳定屈曲应力简化计算公式,采用临界应力法计算了其整体稳定屈曲应力,并根据整体稳定和局部稳定屈曲应力相等的原则给出了Q235和Q460钢H形截面轴压构件局部稳定验算的翼缘和腹板宽厚比限值。
1 有限元分析 1.1 模型介绍和验证材料模型选用abaqus6.10自带的金属塑性plastic来考虑钢材的应力-应变关系。在材性试验的基础上,将应力-应变关系简化为三折线模型,建模时,需要将试验测得的名义应力和应变转化为真实应力和真实应变[14]。名义应力与真实应力,名义应变与真实应变之间的转化分别由式(1)和式(2)给出:
| $ \sigma \text{=}{{\sigma }_{\text{nom}}}\left(1+{{\varepsilon }_{\text{nom}}} \right), $ | (1) |
| $ \varepsilon \text{=}\ln \left(1+{{\varepsilon }_{\text{nom}}} \right), $ | (2) |
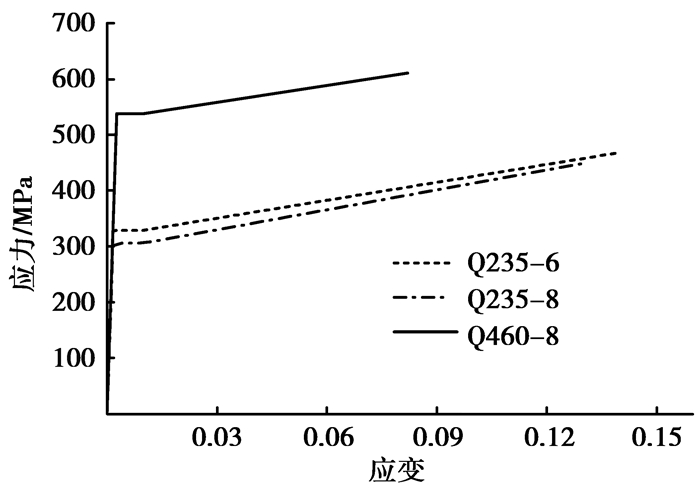
其中,σnom,εnom分别为试验测得的名义应力和名义应变。转化后得到6 mm厚Q235钢板、8 mm厚Q235钢板和8 mm厚Q460钢板的应力应变关系,如图 1所示。
|
图 1 常温下应力应变关系 Figure 1 Stress-strain relationship at room temperature |
单元采用四节点缩减积分壳单元S4R,为满足计算精度的要求,每个单元沿厚度方向取5个积分点,单元的厚度按板件实测厚度选用。考虑残余应力的施加方便和残余应力在整个截面内力平衡的需要,将构件的翼缘划分为18个单元,腹板划分为20个单元。有限元网格的划分如图 2所示。

|
图 2 有限元模型网格划分 Figure 2 Mesh of the FEM |
荷载均匀施加到一端端板上,该端板不约束沿荷载方向的位移,仅约束沿端板平面内的位移,另一端板约束所有方向的节点位移。荷载的施加采用ABAQUS6.10中的pressure模块,在端板上施加均匀压力。
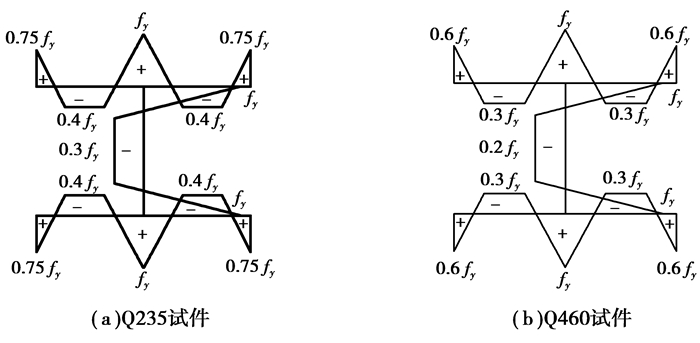
常温下,Q235钢构件的残余应力根据文献[15]施加,Q460钢构件的残余应力综合考虑文献[2, 16-18]施加,Q235和Q460构件的残余应力分布模式如图 3所示。
|
图 3 残余应力分布 Figure 3 Distribution of residual stress |
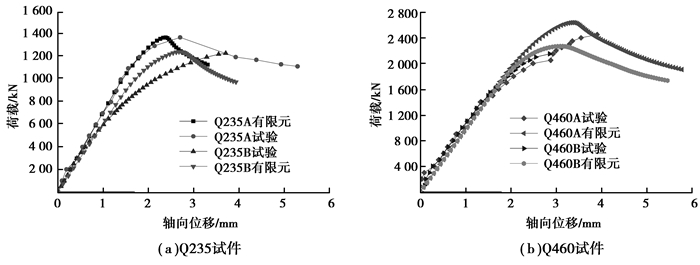
构件的初始几何缺陷根据屈曲分析得到的一阶屈曲模态(如图 4所示)按照0.1倍板厚的幅度施加。有限元分析得到的常温下试件的荷载-位移曲线和破坏模式与试验结果的对比如图 5~图 6所示,可以看出,试验测量的荷载位移曲线和破坏模式与有限元分析的结果比较接近,在弹塑性阶段2个试件稍有偏差,主要原因可能是试验中端板的不平整造成和有限元模型不完全一致。表 1中给出了有限元分析得到的屈曲应力和试验结果的对比,总体吻合较好,最大差异为8%。

|
图 4 一阶屈曲模态 Figure 4 First buckling mode |
|
图 5 常温下试验和有限元分析得出的荷载位移曲线对比 Figure 5 Load-displacement curve comparison at room temperature between experiment and finite element analysis |

|
图 6 常温下构件的破坏 Figure 6 Failure of specimens at room temperature |
| 表 1 常温下试件极限承载力 Table 1 Ultimate load at room temperature |
分析高温下的局部稳定时,有限元模型和常温下一样,仅材料参数不同,对Q235钢构件,采用EC3的材性数据和应力-应变关系模型,对Q460钢构件,根据文献[20]的研究成果,温度低于540 ℃时,采用EC3的材性数据和应力应变关系模型,温度大于540 ℃时,对EC3的材性数据按照文献[20]进行折减。
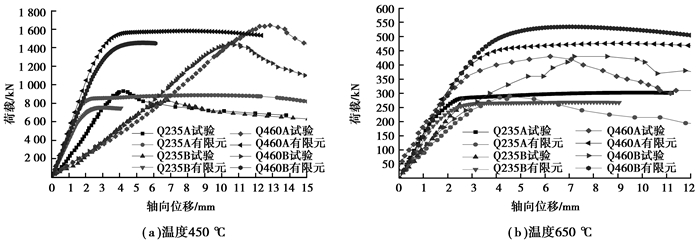
表 2为高温下有限元分析得到的屈曲应力结果和试验结果。可以看出,二者吻合较好,最大差异为11%。试验测得的荷载位移曲线和有限元结果的对比如图 7所示,有限元分析得到的抗压刚度与试验结果差别较大,主要原因一是有限元模型中的高温弹性模量的取值与试验构件高温下的实际值差异较大;二是试验试件制作和加载位置的误差导致试件弯曲或荷载偏心。但屈曲应力结果吻合较好,因此上述有限单元模型可以用于轴心受压构件高温下的局部稳定屈曲应力计算。
| 表 2 试件高温下的屈曲应力 Table 2 Ultimate load of specimens at elevated temperature |
|
图 7 高温下试验和有限元分析得出的荷载位移曲线对比 Figure 7 Load-displacement curve comparison at elevated temperature between experiment and finite element analysis |
分析高温下的局部稳定时,有限元模型和常温下一样,仅材料参数不同,对Q235钢构件,采用EC3的材性数据和应力-应变关系模型,对Q460钢构件,根据文献[20]的研究成果,温度低于540 ℃时,采用EC3的材性数据和应力应变关系模型,温度大于540 ℃时,对EC3的材性数据按照文献[20]进行折减。
表 2为高温下有限元分析得到的屈曲应力结果和试验结果。可以看出,二者吻合较好,最大差异为11%。试验测得的荷载位移曲线和有限元结果的对比如图 7所示,有限元分析得到的抗压刚度与试验结果差别较大,主要原因一是有限元模型中的高温弹性模量的取值与试验构件高温下的实际值差异较大;二是试验试件制作和加载位置的误差导致试件弯曲或荷载偏心。但屈曲应力结果吻合较好,因此上述有限单元模型可以用于轴心受压构件高温下的局部稳定屈曲应力计算。
1.2 参数分析影响轴心受压钢构件局部稳定屈曲应力的因素包括翼缘宽厚比、腹板高厚比、温度、初始几何缺陷、残余应力等。文中从宽厚比与温度,腹板和翼缘相互约束作用,初始缺陷等几个方面进行分析。
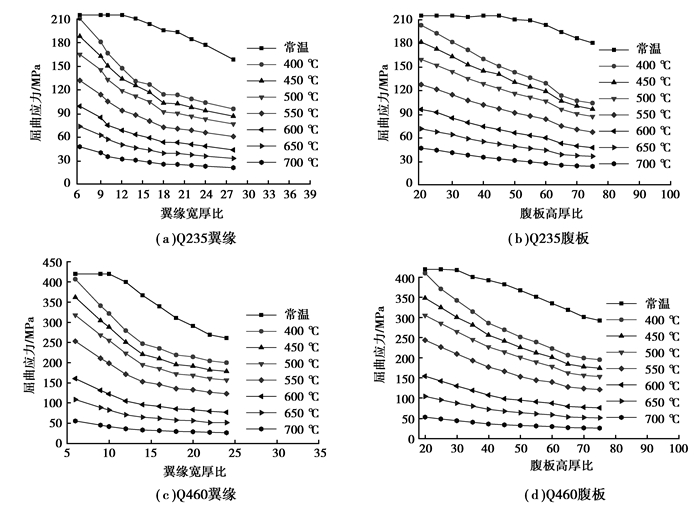
1.2.1 宽厚比和温度采用文中建立的有限元模型分析了多个温度下Q235和Q460钢构件不同宽厚比和高厚比的局部稳定屈曲应力,如图 8所示。可以看出,高温下,当翼缘宽厚比较小时,翼缘屈曲应力随着翼缘宽厚比的增大迅速下降,当翼缘宽厚比较大时,翼缘屈曲应力随翼缘宽厚比的增大减小缓慢,对于腹板屈曲应力,也有类似的趋势。此外,对比Q235与Q460轴压构件常温下局部屈曲应力可以发现,翼缘屈曲应力和腹板屈曲应力达到屈服强度对应的最大宽厚比或高厚比,Q460钢构件的翼缘宽厚比或腹板高厚比均小于Q235轴压构件。例如,对于翼缘屈曲应力达到屈服强度对应的最大宽厚比,Q235试件为12,而Q460试件为10。
|
图 8 局部屈曲应力随宽厚比和高厚比的关系 Figure 8 Effect of width-to-thickness or height-to-thickness ratio on local buckling stress |
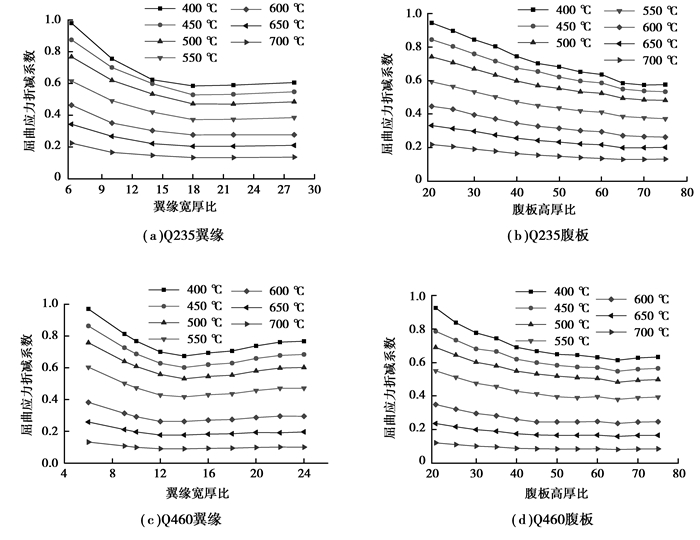
图 9为高温下翼缘屈曲应力和腹板屈曲应力折减系数随板件宽厚比的变化曲线,屈曲应力折减系数是指高温下的屈曲应力和常温下屈曲应力的比值。可以看出,当温度为400 ℃到550 ℃之间时,该系数随板件宽厚比的增加下降较快,对翼缘屈曲的构件,当翼缘宽厚比较小时,屈曲应力折减系数随着宽厚比的增大迅速减小,当翼缘宽厚比为18(Q235钢构件)和15(Q460钢构件)时,该系数取得最小值,之后随着翼缘宽厚比的增大,该系数缓慢增大。对腹板屈曲的构件,屈曲应力折减系数随高厚比的增加而一直降低,温度越低,降低的幅度越明显。
|
图 9 屈曲应力折减系数随宽厚比和高厚比的关系 Figure 9 Effect of width-to-thickness or height-to-thickness ratio on buckling stress reduction factor |
H形截面钢构件的腹板或翼缘局部屈曲时,只要二者的屈曲应力不等,那么屈曲部分必然受到未屈曲部分的约束。工程实际中,H形截面一般由较薄的腹板和较厚的翼缘板焊接而成,当翼缘板屈曲时,腹板对翼缘板的约束作用有限,在常温或高温下,腹板对翼缘的约束作用可以忽略。文中仅考虑腹板屈曲时,翼缘板对腹板的约束作用。
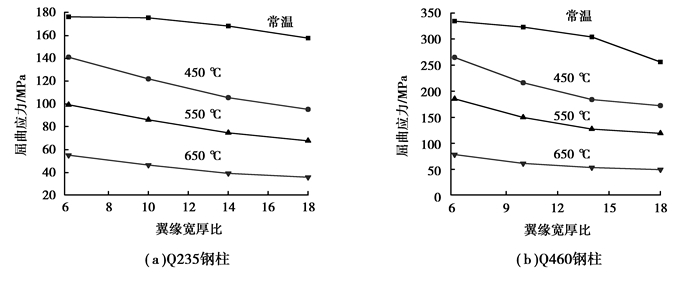
图 10为腹板高厚比为70,不同温度下Q235和Q460钢构件腹板屈曲应力随翼缘宽厚比的变化曲线。为保证翼缘对腹板的有效约束,在确定翼缘宽厚比时,保证翼缘屈曲应力大于腹板的屈曲应力,这样得到腹板的屈曲应力,翼缘尚未屈曲。常温下Q235钢构件,当翼缘宽厚比为6时,腹板的屈曲应力为176.4 MPa,翼缘宽厚比增大到18时,腹板的屈曲应力下降到157.73 MPa,下降了10.6%,而根据弹性理论算得的理想四边简支板件在常温下的屈曲应力152 MPa。翼缘宽厚比从6增大到18时,450 ℃时,屈曲应力下降幅度为32.4%;550 ℃时,屈曲应力的下降比例为31.75%;650 ℃时,屈曲应力的下降达35%。与常温不同的是,随着翼缘宽厚比的增大,腹板屈曲应力的下降由快变慢。对于Q460钢构件,无论高温还是常温下,腹板屈曲应力随翼缘宽厚比的变化大于同样条件下的Q235钢构件。因此,高温下无论是对Q235还是Q460轴压构件,计算腹板屈曲时,应该考虑翼缘约束作用的影响。
|
图 10 翼缘对腹板的约束作用 Figure 10 Restrained effect of the flange on the web |
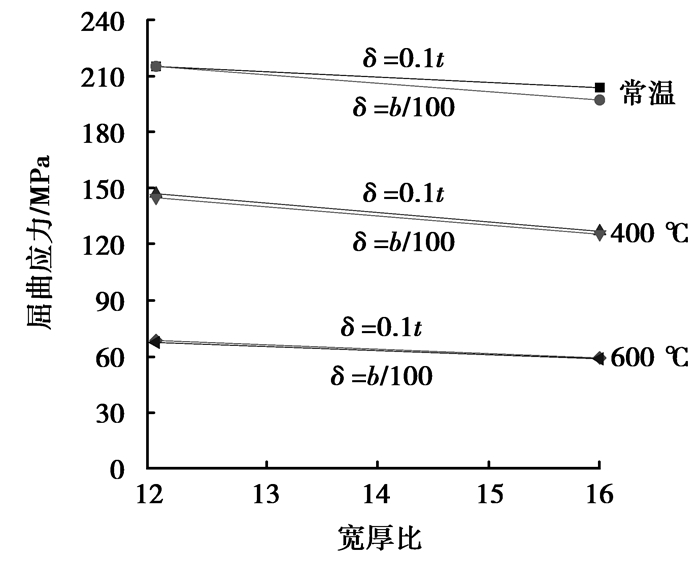
图 8给出的局部屈曲应力都是考虑了0.1 t(t为板厚)的初始几何缺陷,根据Burgess等[21]的研究成果,构件在高温下的热膨胀对构件初始几何缺陷影响较小,可以认为常温下和高温下的几何缺陷一致。中国的《钢结构工程施工质量验收规范》[22]规定的构件的初始几何缺陷的幅度为翼缘板件的外挑宽度的1%,Kaitila等[23]也根据试验结果和经验给出了和中国钢结构施工质量验收规范类似的初始缺陷幅度。为了对比2种缺陷取值对屈曲应力的影响,采用有限元计算了对应的屈曲应力,如图 11所示。屈曲应力可以看出,2种计算结果非常接近,因此,可以采用2组初始缺陷的任意一种分析构件的屈曲应力。
|
图 11 不同初始缺陷下的屈曲应力 Figure 11 Local buckling stress with different initial imperfection |
将图 8的应力和宽厚比正则化。局部屈曲应力系数φ按式(3)计算,板件的正则化宽厚比按式(4)计算:
| $ \varphi=\frac{{{\sigma }_{u}}}{{{f}_{\text{yT}}}}, $ | (3) |
| $ \bar{\lambda }=\frac{b}{t}\sqrt{\frac{12\left(1-{{v}^{2}} \right){{f}_{\text{yT}}}}{k{{\text{ }\!\!\pi\!\!\text{ }}^{2}}{{E}_{\text{T}}}}}, $ | (4) |
式中:fyT为钢材高温下的屈服强度;ET为高温下的弹性模量;k为与边界条件相关的局部屈曲系数,对于翼缘屈曲,可取k=0.425,对于腹板屈曲的情况,可取k=4;υ为钢材的泊松比,取υ=0.3。
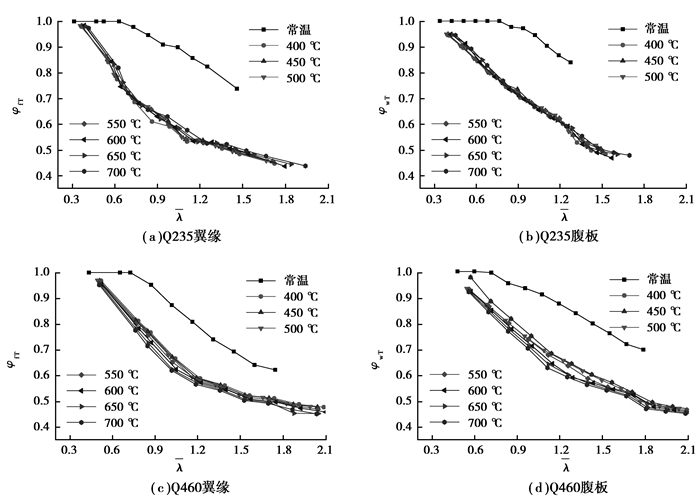
图 12给出了按照上述方法算得的φ-λ曲线。可以看出,温度为400~700 ℃之间时,不同温度下的曲线非常接近,可用1条曲线来描述φ-λ关系。
|
图 12 屈曲应力系数与正则化长细比之间的关系 Figure 12 φ-λ curve of Q235 and Q460 steel members |
根据有限元分析得到的屈曲应力结果,采用数据拟合技术得到了400~700 ℃之间构件局部屈曲应力的计算公式。对任意的H形截面,构件的局部屈曲应力可由式(5)计算:
| $ {{\sigma }_{\text{uT}}}=\left\{ \begin{align} &{{\sigma }_{\text{fuT}}}\ \ \frac{{{h}_{0}}/{{t}_{\text{w}}}}{b/{{t}_{\text{f}}}}<3.07, \\ &{{\sigma }_{\text{wuT}}}\ \ \frac{{{h}_{0}}/{{t}_{\text{w}}}}{b/{{t}_{\text{f}}}}\ge 3.07;\\ \end{align} \right. $ | (5) |
式中:
| $ {{\sigma }_{\text{fuT}}}=\varphi {{\sigma }_{\text{fT}}}{{f}_{\text{yT}}}, $ | (6) |
| $ {{\sigma }_{\text{wuT}}}=\alpha {{\varphi }_{\text{wT}}}{{f}_{\text{yT}}}. $ | (7) |
对Q235轴心受压构件有:
| $ {{\varphi }_{\text{fT}}}=0.4+1.2\text{ }\!\!\times\!\!\text{ }{{0.14}^{{\bar{\lambda }}}}, $ | (8) |
| $ {{\varphi }_{\text{wT}}}=0.19+1.08\text{ }\!\!\times\!\!\text{ }{{0.43}^{{\bar{\lambda }}}}, $ | (9) |
| $ \alpha=0.5+0.15\text{ }\!\!\times\!\!\text{ }\frac{{{h}_{0}}/{{t}_{\text{w}}}}{b/{{t}_{\text{f}}}}-0.006\text{ }\!\!\times\!\!\text{ }{{\left(\frac{{{h}_{0}}/{{t}_{\text{w}}}}{b/{{t}_{\text{f}}}} \right)}^{2}}. $ | (10) |
式中:α为考虑翼缘约束作用的系数;λ为板件的正则化宽厚比,可按式(4)计算。
当翼缘宽厚比小于6,腹板高厚比小于20时,式(8)与式(9)的局部屈曲系数将大于1,因此,当翼缘宽厚比小于6时,可取屈曲系数为1,当腹板高厚比小于20时,可按20计算。当翼缘宽厚比大于28,腹板高厚比大于80时,式(8)到式(10)的适用性有待进一步讨论。
对Q460轴心受压构件有:
| $ {{\varphi }_{\text{fT}}}=0.41+1.35\text{ }\!\!\times\!\!\text{ }{{0.16}^{{\bar{\lambda }}}}, $ | (11) |
| $ {{\varphi }_{\text{wT}}}=0.36+1.14\text{ }\!\!\times\!\!\text{ }{{0.28}^{{\bar{\lambda }}}}, $ | (12) |
| $ \alpha=0.74+0.07\frac{{{h}_{0}}/{{t}_{\text{w}}}}{b/{{t}_{\text{f}}}}. $ | (13) |
式中:α为考虑翼缘约束作用的系数;λ为板件的正则化宽厚比。当翼缘宽厚比小于6,腹板高厚比小于20时,式(11)到式(13)算得的屈曲应力大于钢材的屈服强度,可直接将局部屈曲系数取为1。当翼缘宽厚比大于24,腹板高厚比大于70时,以上公式的适用性有待进一步讨论。
综上所述,式(11)到式(13)可用于腹板高厚比为20~70之间,翼缘宽厚比为6~24之间,温度处于400~700 ℃时,Q460H形截面轴压构件局部稳定承载力的计算。
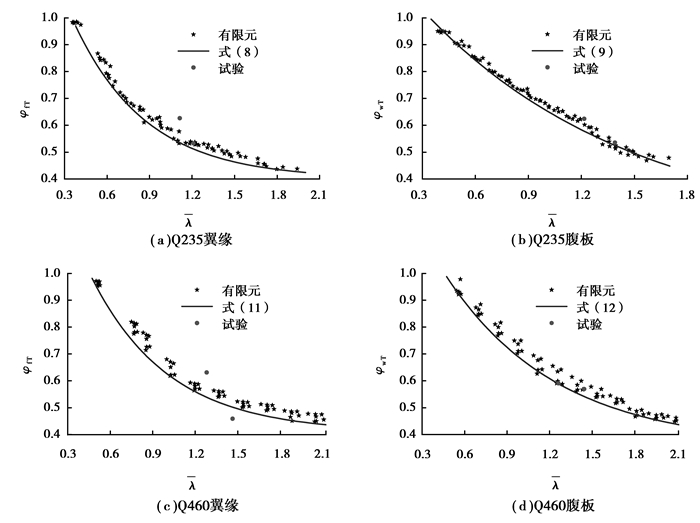
为了验证拟合公式计算结果的可靠性,将式(5)~式(13)算得的屈曲应力和有限元计算结果及试验结果进行了对比,如图 13所示。可以看出对于Q235轴压构件时式(8)~式(10)算得的屈曲应力基本为有限元计算结果和试验结果的下限;对Q460轴压构件,式(11)~式(13)算得的屈曲应力为有限元计算结果的下限,但高于一个试验结果,可能是该试验中加载的偏心和试件的初始缺陷较大造成试验结果较小。
|
图 13 拟合公式与试验结果和有限元结果的对比 Figure 13 Comparison of fitting curve with experimental and finite element analysis results |
工程实践中,很少会针对每个截面计算其局部屈曲应力,通常的做法是在截面选择时,注意选择合适的腹板高厚比和翼缘宽厚比,保证构件满足局部稳定的要求。
高温下,Q235与Q460轴压构件的整体稳定承载力均可由临界应力法计算[24-25]
| $ {{\sigma }_{\text{crT}}}=\frac{1}{2}\left\{ \left(1+{{\text{e}}_{0}} \right){{\sigma }_{\text{eT}}}+{{f}_{\text{yT}}}-\sqrt{{{\left(\left(1+{{\text{e}}_{0}} \right){{\sigma }_{\text{eT}}}+{{f}_{\text{yT}}} \right)}^{2}}-{{f}_{\text{yT}}}{{\sigma }_{\text{E}}}} \right\}, $ | (14) |
式中:σeT为构件高温下的弹性屈曲应力,σeT=π2ET/λ2,对Q235轴压构件,e0按第二类截面取值:e0=0.300λ-0.035,
| $ b/t=4.72+0.6{{\text{e}}^{0.03\lambda }}\left(20\le \lambda \le 100 \right), $ | (15) |
| $ {{h}_{0}}/{{t}_{\text{w}}}=3.9+10.4{{\text{e}}^{0.017\lambda }}\left(20\le \lambda \le 100 \right), $ | (16) |
| $ b/t=5.78+0.11{{\text{e}}^{0.063\lambda }}\left(20\le \lambda \le 80 \right), $ | (17) |
| $ {{h}_{0}}/{{t}_{\text{w}}}=14.8+1.18{{\text{e}}^{0.048\lambda }}\left(20\le \lambda \le 80 \right), $ | (18) |
《钢结构设计规范》GB 50017-2003中给出了常温下,轴心受压构件腹板高厚比和翼缘宽厚比的限值为
| $ \frac{{{h}_{0}}}{{{t}_{\text{w}}}}\le \left(25+0.5\lambda \right)\sqrt{\frac{235}{{{f}_{\text{y}}}}, } $ | (19) |
| $ \frac{b}{{{t}_{\text{f}}}}\le \left(10+0.1\lambda \right)\sqrt{\frac{235}{{{f}_{\text{y}}}}, } $ | (20) |
其中,λ < 30时,按照λ=30取值;λ>100时,按照λ=100取值。
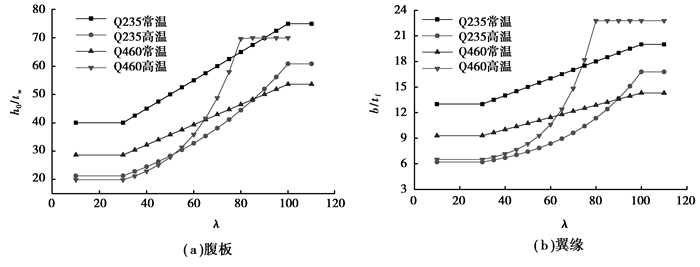
常温和高温下轴心受压构件腹板高厚比和翼缘高厚比限值的对比如图 14所示。可以看出,对Q235轴心受压构件,长细比相等时,高温下的腹板高厚比限值较常温下小,也就是说,高温下的轴心受压构件更容易发生局部屈曲。对Q460轴心受压构件,当构件长细比小于65时,高温下的腹板高厚比限值小于常温下的高厚比限值,当构件长细比大于65时,高温下的腹板高厚比限值较常温下大,也就是说,当构件长细比较小时,高温下的Q460构件更容易发生局部屈曲,长细比较大时,常温下的构件更容易发生局部屈曲。和腹板高厚比限值类似,高温下,Q235翼缘宽厚比的限值偏严;长细比较小时,Q460轴压构件腹板宽厚比限值较常温下严,长细比较大时,翼缘宽厚比限值较常温大。
|
图 14 常温和高温下宽厚比(高厚比)限值的对比 Figure 14 Comparison of width-to-thickness or height-to-thickness ratio at room and elevated temperature |
采用经试验数据验证的有限单元模型,计算了400~700 ℃之间Q235H和Q460H形截面轴心受压构件高温下的腹板屈曲和翼缘屈曲极限承载力,采用参数分析研究了温度、板件宽厚比(翼缘宽厚比和腹板高厚比)、初始缺陷、腹板和翼缘相互作用等因素对构件局部屈曲应力的影响,在参数分析的基础上采用数值分析方法拟合出了Q235和Q460轴心受压构件高温下的局部稳定屈曲应力计算公式,给出了高温下防止构件局部屈曲的宽厚比限值。
1)高温下当板件的宽厚比较小时,构件的局部屈曲应力随板件宽厚比的增大迅速减小,当板件宽厚比较大时,构件的局部屈曲应力随板件宽厚比的增大减小缓慢。
2)采用0.1倍板厚的初始缺陷和1%翼缘外挑宽度的初始缺陷,分析得到的屈曲应力基本相同。
3)高温下腹板屈曲应力随翼缘宽厚比的变化非常明显,即翼缘对腹板的约束作用较常温下更加明显,在计算H形截面构件腹板屈曲应力时,应当考虑这种约束作用。
4)高温下防止板件局部屈曲的板件宽厚比与常温下的限值有所不同,对Q235钢H形截面轴心受压构件,高温下的腹板高厚比限值和翼缘宽厚比限值均较常温下小。对Q460轴心受压构件,当构件长细比较小时,腹板高厚比和翼缘宽厚比限值比常温下小,当构件长细比较大时,腹板高厚比和翼缘宽厚比限值比常温下大。
| [1] |
李国强, 韩林海, 楼国彪. 钢结构及钢-混凝土组合结构抗火设计[M]. 北京: 中国建筑工业出版社, 2006.
LI guoqiang, HAN Linhai, LOU Guobiao. Fire resistance design of steel structure and steel-concrete composite structure[M]. Beijing: China building industry press, 2006. (in Chinese) |
| [2] |
葛勇.约束高强度Q460钢柱抗火性能研究[D].重庆:重庆大学, 2012. GE Yong.Study on fire resistance of restrained high strength Q460 steel column[D].Chongqing :Chongqing Univeristy, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10611-1012049506.htm |
| [3] | Feng M, Wang Y, Davies J. Davies J.Structural behavior of cold-formed thin-walled short steel channel columns at elevated temperatures.Part 1: Experiments[J]. Thin-Walled Structures, 2003, 41(6): 543–570. DOI:10.1016/S0263-8231(03)00002-8 |
| [4] | Feng M, Wang Y, Davies J. Axial strength of cold-formed thin-walled steel channels under non-uniform temperatures in fire[J]. Fire Safety Journal, 2003, 38(8): 679–707. DOI:10.1016/S0379-7112(03)00070-5 |
| [5] | Feng M, Wang Y, Davies J. Structural behavior of cold-formed thin-walled short steel channel columns at elevated temperatures.Part 2: Design calculations and numerical analysis[J]. Thin-Walled Structures, 2003, 41(6): 571–594. DOI:10.1016/S0263-8231(03)00003-X |
| [6] | Heidarpour A, Bradford M. Local buckling and slenderness limits for flange outstands at elevated temperatures[J]. Journal of Constructional Steel Research, 2007, 63(5): 591–598. DOI:10.1016/j.jcsr.2006.07.007 |
| [7] | Heidarpour A, Bradford M. Local buckling and slenderness limits for steel webs under combined bending, compression and shear at elevated temperatures[J]. Thin-Walled Structures, 2008, 46(2): 128–146. DOI:10.1016/j.tws.2007.08.014 |
| [8] | Knobloch M, Fontana M. Strain-based approach to local buckling of steel sections subjected to fire[J]. Journal of Constructional Steel Research, 2006, 62(1/2): 44–67. |
| [9] | ANSI/AISC360-10.Specification for structural steel buildings[S].2010. |
| [10] | Eurocode 3: Design of steel structures-Part 1.2: General rules-structural fire design[S].2005. |
| [11] |
GB50017-2003.钢结构设计规范[S].北京:中国计划出版社, 2003. GB50017-2003.Code for Design of Steel Structures[S].Beijing: China planning press, 2003. |
| [12] |
CECS200-2006, 建筑钢结构防火技术规范[S].北京:中国计划出版社, 2006. CECS200-2006, Code for Fire safety of Steel Building Structures[S].Beijing: China planning press, 2006. |
| [13] |
王卫永, 杨兴才, 王彬, 等.
轴心受压钢构件高温下的局部稳定试验研究[J]. 建筑结构学报, 2014, 35(11): 134–142.
WANG Weiyong, YANG xingcai, WANG Bin, et al. Experimental study on local stability of axially compressed steel members at elevated temperature[J]. Journal of building structures, 2014, 35(11): 134–142. (in Chinese) |
| [14] |
庄茁, 张帆. 基于abaqus的有限元分析和应用[M]. 北京: 清华大学出版社, 2009.
ZHUANG Zhuo, ZHANG Fan. Based on abaqus finite element analysis and application[M]. Beijing: Tsinghua university press, 2009. (in Chinese) |
| [15] |
陈骥. 钢结构稳定理论与设计[M]. 北京: 科学出版社, 2011.
CHEN Ji. Steel structure stability theory and design[M]. Beijing: Science press, 2011. (in Chinese) |
| [16] | WANG Yanbo, LI Guoqiangi, CHEN Suwen. Residual stresses in welded flame-cut high strength steel h-sections[J]. Journal of constructional steel research, 2012, 79: 159–165. DOI:10.1016/j.jcsr.2012.07.014 |
| [17] |
童乐为, 赵俊, 周锋, 等.
Q460高强度焊接H型钢残余应力试验研究[J]. 工业建筑, 2012, 42(001): 51–55.
TONG Lewei, ZHAO Jun, ZHOU Feng, et al. Experimental investigation on longitudinal residual stress of q460 high-strength steel welded h-section members[J]. Industrial Buildings, 2012, 42(001): 51–55. (in Chinese) |
| [18] |
班慧勇, 施刚, 石永久, 等.
超高强度钢材焊接截面残余应力分布研究[J]. 工程力学, 2008, 25(Sup02): 57–61.
BAN Huiyong, SHI Gang, SHI Yongjiu, et al. Study on the residual stress distribution of ultra high strength steel welded sections[J]. Engineering Mechanics, 2008, 25(Sup02): 57–61. (in Chinese) |
| [19] | Kwon Y B, Hancock G J. A nonlinear elastic spline finite strip analysis for thin-walled sections[J]. Thin-Walled Structures, 1991, 12(4): 295–319. DOI:10.1016/0263-8231(91)90031-D |
| [20] | Chen J, Young B, Uy B. Behavior of high strength structural steel at elevated temperatures[J]. Journal of Structural Engineering, 2006, 132(12): 1948–1954. DOI:10.1061/(ASCE)0733-9445(2006)132:12(1948) |
| [21] | Burgess I, Olawale A, Plank R. Failure of steel columns in fire[J]. Fire Safety Journal, 1992, 18(2): 183–201. DOI:10.1016/0379-7112(92)90037-D |
| [22] |
GB50205.钢结构工程施工质量验收规范[S].北京:中国计划出版社, 2002. GB50205-2001.Check & Accept Specification for Steel Structure Work[S].Beijing: China planning press, 2003. |
| [23] | Kaitila O. Imperfection sensitivity analysis of lipped channel columns at high temperatures[J]. Journal of Constructional Steel Research, 2002, 58(3): 333–351. DOI:10.1016/S0143-974X(01)00060-8 |
| [24] |
刘兵, 王卫永, 李国强, 等.
高强度H460钢柱抗火性能研究[J]. 土木工程学报, 20124, 45(9): 19–26.
LIU Bing, WANG Weiyong, LI Guoqiang., et al. Study of fire resistance of high strength Q460 steel columns[J]. Journal of civil engineering, 20124, 45(9): 19–26. (in Chinese) |
| [25] |
王卫永, 李国强, 戴国欣.
轴心受压高强度H型钢柱抗火性能[J]. 重庆大学学报, 2010, 33(10): 76–81.
WANG Weiyong, LI Guoqiang, DAN Guoxin. Fire-resistance performance of high-strength-steel H shaped columns under the axial compression[J]. Journal of Chongqing University, 2010, 33(10): 76–81. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38

