节点位置信息在无线传感器网络(wireless sensor network,WSN)的各种应用中占据着非常重要的位置。如目标的检测与跟踪、网络拓扑的自动配置[1]等。根据定位过程是否需要测距,目前的定位算法被分为基于测距和无需测距两大类[2]。基于测距的定位算法对传感器节点的硬件要求高,定位精度也高,典型的有RSSI,AOA,TOA,TDOA。无需测距的定位算法对传感器节点的硬件要求低,但定位精度较低,典型的算法有DV-Hop算法、质心算法、APIT算法等。由于后者成本低,无需额外硬件,因此,更适合于大规模无线传感器网络的实际应用[3]。
DV-Hop算法是无线传感器网络节点定位中应用最广泛的一种算法。但该算法定位精度较低,因此,很多学者对其进行了改进,Lu Qingling等人[4]提出了对平均每条距离进行加权处理;Li Wenwen等人[5]在DV-Hop算法的定位阶段引进差分进化算法来计算未知节点的位置;林金朝等人[6]等通过泰勒级数展开估算未知节点的位置;王颖等人[7]通过引入网络平均连通度来改进节点间的跳距;杨磊等人[8]等通过角度阀值的设置来筛选锚节点;冯江等人[9]等根据距离未知节点的跳数和环境影响因子对平均每跳距离进行加权处理;杨智锋等人[10]等利用代数重建法取代最小二乘法来计算未知节点的坐标位置。
针对DV-Hop算法中锚节点以及未知节点平均每跳距离引起的误差,结合遗传算法的基本原理,提出了一种基于遗传算法的DV-Hop (GADV-Hop)算法,该算法首先利用遗传算法对锚节点的平均每跳距离加以优化和改进,提高锚节点的平均每跳距离的准确度,然后利用跳数在3跳以内的锚节点的平均每跳距离对未知节点的平均每跳距离进行加权处理,通过提高未知节点平均每跳距离的精确度来提高算法定位的精度,仿真结果证明该算法具有较好的性能。
1 DV-Hop算法美国Niculescu等人[11-12]提出的DV-Hop算法,该算法通过跳数乘以平均跳距得到信标节点和未知节点之间的估算距离,再利用三边测量法估算出未知节点的坐标。定位过程如下
1)锚节点向邻居节点广播包含节点标识号,节点位置以及跳数值的分组{idi, xi, yi, hop}。邻居节点记录下各节点的标识号,坐标值,以及较小的跳数值。转发跳数值加1后的分组。通过此方式,所有节点均获得距离各锚节点的最小跳数。
2)利用式(1)计算各锚节点的平均每跳距离。
| $ {\rm{hopsiz}}{e_i} = \sum\limits_{j \ne i} {\sqrt {{{({x_i}-{x_j})}^2} + {{({y_i}-{y_j})}^2}} /} \sum\limits_{j \ne i} {{\rm{hop}}{s_j}} $ | (1) |
其中:(xi, yi),(xj, yj),hopsj分别表示信标节点i和j的位置以及二者之间的最小跳数。未知节点利用接收到距其最近的锚节点的hopsize乘以最小跳数值hops估算与各锚节点之间的距离。
3)未知节点利用3个或以上的锚节点距离估算自身坐标位置。
2 GADV-Hop算法 2.1 传统DV-Hop算法存在的不足传统DV-Hop算法定位过程实现简单,成本较低,但也存在较大的定位误差。平均每跳距离引起的误差是其中最重要的原因之一。
1)传统DV-Hop算法中计算锚节点平均每跳距离时,利用实际距离与跳数的比值得到。即直线距离表示跳段距离,当节点间跳数越多时,计算得到的跳段距离误差越大。传统DV-Hop并未对其误差进行分析处理,获取误差最小的跳段距离,从而导致跳段距离与实际值相差较大,即得到误差较大的锚节点平均每跳距离。未知节点利用误差较大的锚节点平均每跳距离进行估算节点间距离,从而导致较大的定位误差。
2)未知节点在估算与锚节点之间的距离时仅仅采用距离其最近的锚节点的平均每跳距离。而单个节点无法反映网络的整个属性,而且若该锚节点的平均每跳距离误差很大时,则估算出的与锚节点之间的距离值误差更大。
针对这2方面的不足,对锚节点和未知节点的平均每跳距离的计算方法进行改进。
2.2 遗传算法遗传算法模拟生物的遗传和进化过程[13],按照某种机制,从任一解出发,以一定的概率在整个求解空间中找出最优解,是一种自适应全局优化概率搜索方法。
式(2)的数学规划模型可描述一个求函数最小值的优化问题。
| $ \left\{ \begin{array}{l} \min f(\boldsymbol{X}), \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\boldsymbol{X} \in R, \\ R \subseteq U, \end{array} \right. $ | (2) |
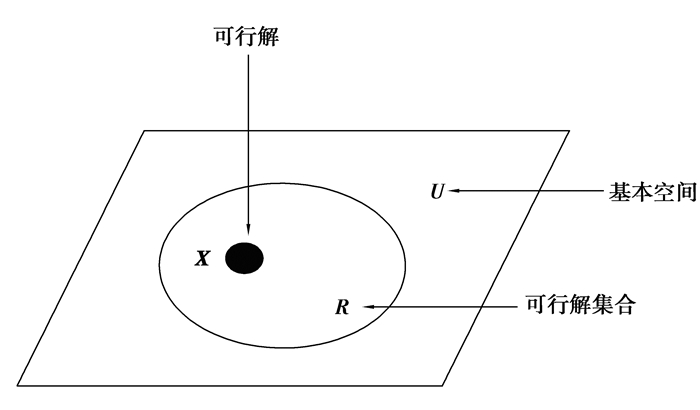
其中:X=[x1, x2, …xn]; T是决策变量; xi是遗传基因; X是一个染色体,由n个遗传基因组成。f(X)为目标函数,对各个XX,其适应度由特定规则制订,关联于X的目标函数值,越靠近目标函数的最优点,X适应度越大,反之亦然。U为基本空间,R为U的子集。
可行解指的是满足约束条件X的解,R为可行解集合,二者关系如图 1所示。问题的搜索空间由所有的染色体X组成。通过搜索染色体X得到问题的最优解。
|
图 1 可行解与可行解集合关系图 Figure 1 Relation schema of feasible solution and feasible solution set |
遗传算法主要由3种运算实现:
选择运算:按照一定的规则或方法,根据个体的适应度,从第t代群体P(t)中选择优良个体遗传至下一代群体P(t+1)中;
交叉运算:群体P(t)内的每个个体被随机搭配成对,每一对以交叉概率相互交换部分染色体;
变异运算:P(t)中所有个体以变异概率改变某个或某些基因座上的基因值。
搜索空间的全局搜索和局部搜索通过交叉运算和变异运算相互配合完成。
2.3 锚节点平均每跳距离的改进DV-Hop算法的定位精度主要取决与定位过程中平均每跳距离的准确度。目前,平均每跳距离的计算在很多改进的DV-Hop算法中均基于无偏估计准则。而嵇玮玮等人[13]计算平均每跳距离时基于均方误差准则,而且证明了该准则比无偏估计准则更为合理。因此,构造计算平均每跳距离的数学模型时基于最小均方误差准则,并利用遗传算法进行求解。
根据记录的节点位置信息,锚节点利用式(3)计算出锚节点i与j之间的实际距离
| $ {d_{tij}} = \sqrt {{{({x_i}-{x_j})}^2} + {{({y_i}-{y_j})}^2}} 。 $ | (3) |
锚节点i与j之间的估算距离等于第一阶段得到的最小跳数与利用式(1)得到的平均每跳距离相乘即可得到,即deij=hopsij×hopesizei。ε=|dtij-deij|为deij=hopsij×hopesizei引起的误差。合理的hopesizei应使ε最小,因此,hopesizei计算变成求最小值问题。数学模型如式(4)所示。
| $ \left\{ \begin{array}{l} {\rm{Min}}\;\;\;\varepsilon = \sum\limits_{i \ne j} {{{({d_{ij}}-{\rm{hopsiz}}{e_i} \times {\rm{ho}}{{\rm{p}}_{ij}})}^2}, } \\ s.t.\;\;\;\;0 \le {\rm{hopsiz}}{e_i} \le \max ({d_{ij}}), \end{array} \right. $ | (4) |
遗传算法中各个个体遗传机会的大小由个体适应度的大小来决定。在本算法中,目标函数以求函数最小值为优化目标且总取非负值,因此将目标函数值取作个体的适应度,采用式(5)作为遗传算法中的的适应度函数来求解锚节点i对应的平均每跳距离hopesizei。
| $ f({\rm{hopsiz}}{e_i}) = \sum\limits_{i \ne j} {{{({d_{ij}}- {\rm{hopsiz}}e \times {\rm{ho}}{{\rm{p}}_{ij}})}^2};} \;\;\;\;\;\;{\rm{hopsiz}}{e_i} \in [0, {\rm{max(}}{d_{ij}}{\rm{)}}]\;。 $ | (5) |
基于以上分析,锚节点的平均每跳距离hopesizei计算步骤如下
1) 在解空间[0, max (dij)]内随机生成初始种群(解集)t;
2) 利用式(4)评价种群中的所有个体(解);
3) 根据评估结果对被选种群进行升序排列,取前20%的最优个体进行单点交叉和基本位变异,从而得到更优的新种群t+1;
4) 若迭代次数达到了设定的最大次数或达到最小的错误,转向5),否则用新的种群t+1取代种群t,返回步骤2)继续执行;
5) 输出最优解到变量hopesizei。
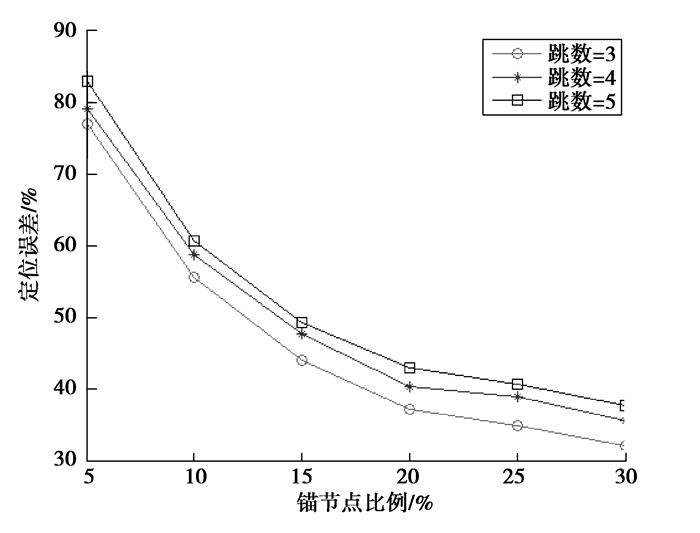
2.4 未知节点平均每跳距离的加权处理单个锚节点的平均每跳距离无法反映整个网络的真实属性。基于此,GADV-Hop算法在计算未知节点的平均每跳距离时,采用多个锚节点而不是单个锚节点的平均每跳距离计算其平均每跳距离,定位误差随着最小跳数的增加而增大[14],不同跳数对GADV-Hop算法影响如图 2所示。
|
图 2 跳数对定位误差的影响 Figure 2 The influence of jump number on the position error |
从图 2可以看出,当跳数为3时,GADV-Hop算法定位误差最小,因此,取跳数为3以内的锚节点平均跳距来加权处理未知节点的平均每跳距离。具体步骤如下:
1) 锚节点计算出最优的hopesizei后,在网络中广播分组{idi, hopesizei};
2) 未知节点对照表中记录的id以及对应的hop,仅记录下跳数小于等于3的锚节点的hopesizei;
3) 广播结束后,未知节点收到所有跳数小于等于3的锚节点的hopesizei;
4) 未知节点利用式(6)计算各锚节点的权值
| $ {w_i} = \frac{{\frac{1}{{{\rm{ho}}{{\rm{p}}_i}}}}}{{\sum\limits_{i = 1}^N {\frac{1}{{{\rm{ho}}{{\rm{p}}_i}}}} }}, $ | (6) |
式中:N为跳数小于等于3的锚节点个数,hopi为锚节点i与未知节点的最小跳数值。
5)利用式(7)加权处理未知节点的平均每跳距离,
| $ {\rm{avg\_hopsize = }}\sum\limits_{i = 1}^N {{\rm{hopsiz}}{e_i}{w_i}。} $ | (7) |
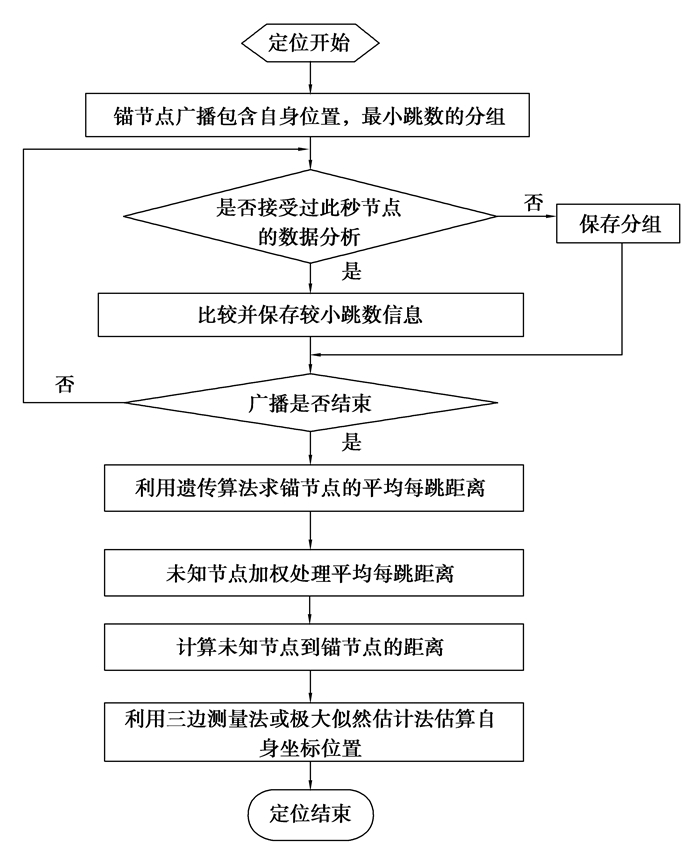
引进遗传算法计算锚节点平均每跳距离并对未知节点的平均每跳距离进行加权处理后,GADV-Hop算法定位流程如图 3所示。
|
图 3 GADV-Hop算法计算平均每跳距离的流程 Figure 3 Process of GADV-Hop algorithm for calculating the average distance per hop |
实验采用MATLAB7.0对算法进行仿真验证。锚节点和未知节点随机分布在区域为:[0, 100]×[0, 100]的网络中,初始节点分布如图 4所示。
|
图 4 节点初始分布图 Figure 4 Distribution map of node initial |
遗传算法中,初始的种群太小得不到可行解,太大会导致计算量的增加;交叉概率用于控制交叉操作的频率,太小导致搜索停滞,太大会破坏适应度高的个体;而变异概率太小不能生成新的个体,太大则搜索随机性过大。经过多次实验验证,初始种群选为50,交叉概率选为0.4,变异概率选为0.2,迭代次数为25时较为合理。
定位精度是衡量定位算法优劣的重要指标,本文通过定位误差和归一化定位误差两个方面,比较GADV-Hop算法与DV-Hop算法的定位精确度和稳定性。
定位误差[15]定义为
| $ {\rm{avg\_error}} = 100\% \times \frac{{\left| {{\boldsymbol{X}_i}-\boldsymbol{X}{\boldsymbol{'}_i}} \right|}}{R}, $ | (6) |
归一化定位误差定义为
| $ {\rm{error}} = \frac{{\sum\limits_{i = 1}^N {\left| {{\boldsymbol{X}_i}-\boldsymbol{X}{\boldsymbol{'}_i}} \right|} }}{{NR}}, $ | (7) |
式中:Xi,X′i分别代表节点i的实际坐标和计算出来的坐标,N为未知节点数,R为通信半径。
3.2 仿真结果分析针对不同的锚节点比例,不同节点总数和不同的通信半径3种情况下作仿真实验,比较改进算法(GADV-Hop)与传统DV-Hop算法的性能。
1)锚节点比例不同
在网络区域中分别随机分布200个节点,保持节点总数不变,锚节点的比例从5%逐渐增加至40%,通信半径取R=10 m,比较两种算法的定位误差,仿真结果如图 5所示。
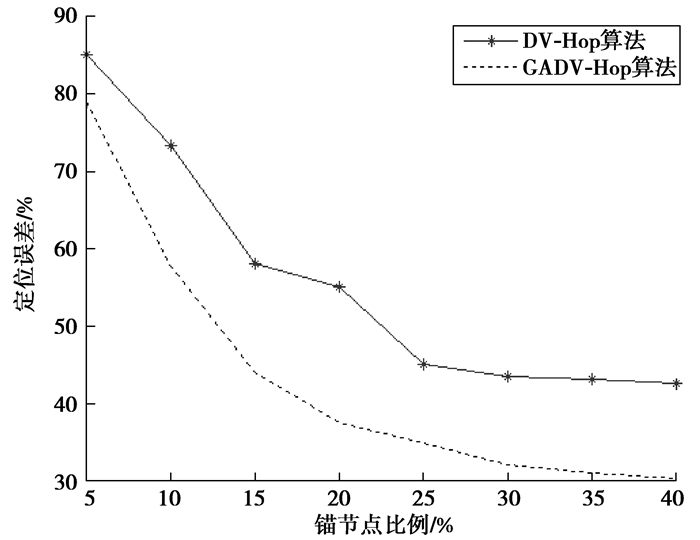
|
图 5 锚节点比例与定位误差比较 Figure 5 Comparison between anchor node proportion and position error |
从图 5中可以看出,在锚节点比例较少时,GADV-Hop算法比传统的DV-Hop算法定位误差小,但相差不是很大。随着锚节点比例的增加,两种算法的平均定位误差均逐渐降低,由于GADV-Hop算法引入遗传算法来计算平均每跳距离,并采用多个锚节点的平均每跳距离加权处理未知节点的平均每跳距离,减少了由平均每跳距离引起的误差,使未知节点与锚节点之间估算的距离更接近实际距离,因而,改进算法比传统的DV-Hop算法定位误差减少的幅度更大。很显然,改进算法的性能明显优于传统的DV-Hop算法,改进算法的定位误差比传统的DV-Hop算法平均降低了10.9%。
2)节点数量不同
在网络区域中分别随机分布200个节点,通信半径取R=10 m,锚节点比例为10%,通过改变节点数量,锚节点比例保持不变,比较GADV-Hop算法与传统DV-Hop算法2种算法的性能,仿真结果如图 6所示。
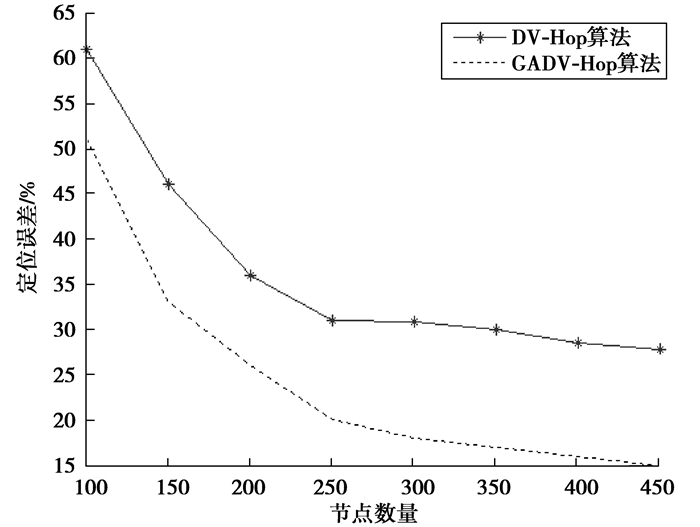
|
图 6 节点总数与定位误差比较 Figure 6 Comparison between total node number and positioning error |
从图 6中可以看出,随着节点数量的增加,两种算法的定位误差都在降低,在节点总数为300之后,误差趋向平稳,改变不大。但GADV-Hop算法定位精度明显优于传统DV-Hop算法,GADV-Hop算法定位精度比传统DV-Hop算法定位误差平均降低了13%。
3)通信半径不同
其它条件相同,通信半径发生改变的情况下,比较GADV-Hop算法与传统DV-Hop算法的性能。仿真结果如图 7、图 8所示。
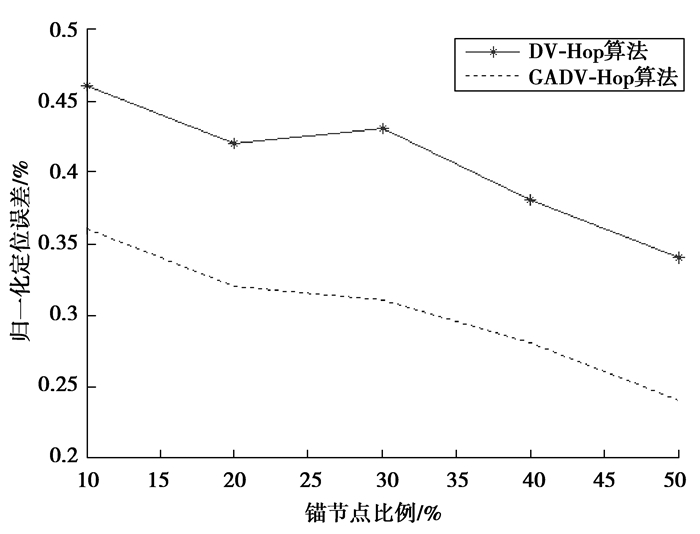
|
图 7 R=15 m归一化定位误差 Figure 7 R=15 m normalizad positioning error |
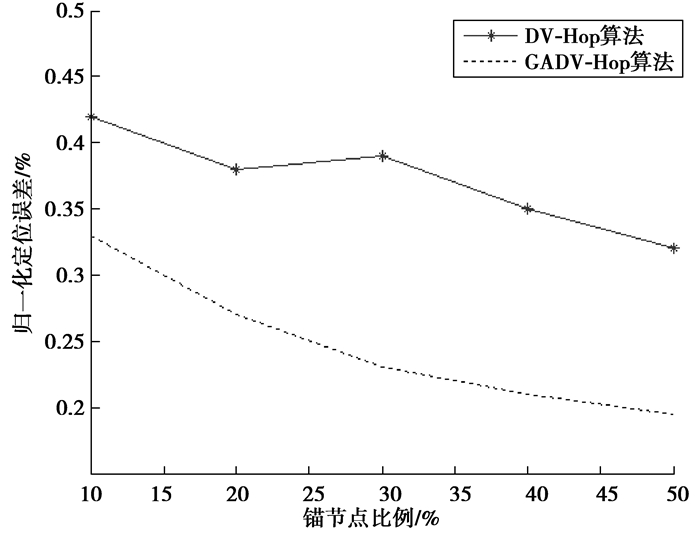
|
图 8 R=20 m归一化定位误差 Figure 8 R=20 m normalizad positioning error |
从图 7、图 8中可以看出,节点之间相互通信的概率随着通信半径的增加而增大,因此,两种算法的归一化定位误差均逐渐减低,但GADV-Hop算法由于改进了平均每跳距离的计算方法,在相同条件下,GADV-Hop算法性能明显优于DV-Hop算法,归一化定位误差比DV-Hop算法平均下降了7%~10%。
4)算法复杂度分析
表 1给出了GADV-Hop算法与传统DV-Hop算法在复杂度以及通信开销方面的性能比较。设网络中节点总数为K,信标节点数为N。通信半径为20 m,锚节点比例为15%时的数据,算法通信开销及复杂度如表 1所示。因为改进算法只是在锚节点计算平均每跳距离时采用GA算法进行,因此, 稍微增加了计算量,而数据包的传送路径、数据包的数量均未变化,因而通信开销没有增加。从表 1中可看出与传统DV-Hop算法相比,GADV-Hop算法在没有增加通信开销的情况下,以较小的计算量代价取得了更高的定位精度。
| 表 1 两种算法性能比较P Table 1 performance comparison oftwo algorithms |
根据实验结果可知,在相同的网络环境中,GADV-Hop算法的定位精确度得到了有效提高。而且该算法只是在计算平均每跳距离时引入了遗传算法,其余的定位过程与传统的DV-Hop算法一样,因此,实现比较简单,没有增加新的硬件,确保了较低的定位成本,适合用在大规模的无线传感器网络中。
4 结语综上所述,针对DV-Hop算法中平均每跳距离导致的定位误差问题,利用遗传算法的全局优化性能,对平均每跳距离的计算过程进行优化改进,在不增加硬件开销的情况下,提高各个锚节点平均每跳距离的精确度,从而使得未知节点与锚节点之间的估算距离更为准确,从而提高了算法的定位精度。仿真结果表明,改进算法能够有效提高算法的定位精确度,并具有较好的稳定性,算法性能良好, 由于引入了遗传算法,因此增加了一部分计算量,如何降低计算量带来的能耗将做进一步的研究。
| [1] | Chen T M, Sanchez J C, Buford J. Petri netmodeling of cyber-physical attacks on smart grid[J]. IEEE Transactions on Smart Grid, 2011, 2(4): 741–749. DOI:10.1109/TSG.2011.2160000 |
| [2] |
孙利民, 李建中, 陈渝, 等. 无线传感器网络[M]. 北京: 清华人学出版社, 2005: 148-149.
SHUN Limin, LI Jianzhong, CHEN Yu, et al. Wireless sensor network[M]. Beijing: Tsinghua University to Study Press, 2005: 148-149. (in Chinese) |
| [3] |
王福豹, 史龙, 任丰原.
无限传感器网络中的自身定位系统和算法[J]. 软件学报, 2003, 16(5): 857–868.
WANG Fubao, SHI Long, REN Fengyuan. Infinite own positioning system and the algorithm of sensor networks[J]. Journal of Software, 2003, 16(5): 857–868. (in Chinese) |
| [4] | Lu Q L, Bai M L, Zhang W, et al. A kind of improved DV-Hop algorithm[C]//Proceedings of the 2nd International Conference on Inteligent Control and Information Processing. Harbin, China:IEEE, Press, 2011:867-869. |
| [5] | Li W W, Zhou W N. Genetic algorithm base localization algorithm for wireless sensor network[C]//Proceedings of 2011 Seventh International Conference on Natural Computation.Shanghai, China, 2011:2096-2099. |
| [6] |
林金朝, 李小玲, 刘海波.
无线传感器网络DV-Hop算法改进与性能[J]. 重庆大学学报, 2010, 33(2): 127–132.
LIN Jinchao, LI Xiaoling, LIU Haibo. Wireless sensor network DV-Hop performance improvement and algorithm[J]. Journal of Chongqing University, 2010, 33(2): 127–132. (in Chinese) |
| [7] |
王颖, 石昊旸.
改进的无线传感器网络DV-Hop定位算法[J]. 计算机工程, 2012, 38(7): 66–69.
WANG Ying, SHI Haoyang. Improvement of DV-Hop wireless sensor network localization algorithm[J]. Computer Engineering, 2012, 38(7): 66–69. (in Chinese) |
| [8] |
杨磊, 张政保, 谢桂海, 等.
基于角度阈值的改进型DV-Hop定位算法[J]. 计算机工程, 2008, 34(20): 96–98.
YANG Lei, ZHANG Zhengbao, XIE Guihai, et al. Based on the modified threshold value from the Angle of DV-Hop localization algorithm[J]. Computer Engineering, 2008, 34(20): 96–98. (in Chinese) |
| [9] |
冯江, 朱强, 吴春春.
改进的DV-Hop定位算法研究[J]. 计算机工程, 2012, 38(19): 74–77.
FENG Jiang, ZHU Qiang, WU Chunchun. Improvement of DV-Hop localization algorithm study[J]. Computer Engineering, 2012, 38(19): 74–77. (in Chinese) |
| [10] |
杨智锋, 裴腾达, 裴炳南, 等.
基于代数重建法的DV-Hop定位算法[J]. 计算机工程, 2010, 36(15): 117–119.
YANG Zhifeng, PEI Tengda, PEI Bingnan, et al. DV-Hop positioning algorithm based on algebraic reconstruction technique[J]. Computer Engineering, 2010, 36(15): 117–119. (in Chinese) |
| [11] | Niculescu D, Nath B. DV based positioning in ad hoc networks[C]. Journal of Telecommunication Systems, 2003, 22 (1-4):267-280. |
| [12] | Vasconcelos J A, Ramirez J A, Takahashi R H C, et al. Improvements in genetic algorithms[J]. IEEE Trans on Magnetics, 2001, 37(5): 3414–3417. DOI:10.1109/20.952626 |
| [13] |
嵇玮玮, 刘中.
DV-Hop定位算法在随机传感器网络中的应用研究[J]. 电子与信息学报, 2008, 30(4): 970–974.
JI Weiwei, LIU Zhong. DV-Hop localization algorithm in the application of stochastic sensor network research[J]. Journal of Electronics & Information Technology, 2008, 30(4): 970–974. (in Chinese) |
| [14] |
周天绮, 姜凤茹.
基于MPSO-DV-Hop的无线传感器节点定位[J]. 计算机工程与应用, 2013, 49(23): 55.
ZHOU Tianqi, JIANG Fengru. Based on MPSO-DV-Hop of wireless sensor node localization[J]. Computer engineering and application, 2013, 49(23): 55. (in Chinese) |
| [15] |
王新生, 赵衍静, 李海涛.
基于DV-Hop定位算法的改进研究[J]. 计算机科学, 2011, 38(2): 76–78.
WANG Xinsheng, ZHAO Yanjing, LI Haitao. Based on DV-Hop localization algorithm to improve research[J]. Journal of Computer Science, 2011, 38(2): 76–78. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38

