汽车空气动力特性是汽车的重要特性之一,它直接影响汽车的动力性、燃油经济性、操纵稳定性、舒适性和安全性。改善汽车的空气动力性能不仅能提高汽车动力性,而且可以改善燃油经济性[1]。
应用仿生学原理,改变物体表面形态,通过改变附壁区流体的运动学和动力学特性,控制边界层的流场结构,减小能量的损耗,从而达到减小气动阻力的目的,不需要增加附加设备及能量消耗,也不会造成流体污染,因此,在车身气动减阻中引入表面非光滑形态结构减阻是一个值得深究的课题[2-5]。
目前常见的非光滑表面结构主要有3种:凹坑型非光滑单元体、凸包型非光滑单元体和沟槽型非光滑单元体[6]。但是非光滑单元体结构特征参数的设计缺少有效和可靠的方法,结合之前的研究,布置在MIRA阶梯背模型尾部的凹坑型非光滑单元体减阻效果明显。因此,文中选择在MIRA阶梯背模型尾部分别布置凹坑型、凸包型及沟槽型3种非光滑单元体,分析其减阻效果,并分别对3种非光滑单元体进行优化,以寻求更优的减阻效果,证明该优化设计方法的有效性和可靠性,为非光滑形态结构特征参数设计的后续理论研究和工程应用提供参考和方法依据。
1 非光滑单元体尺寸设计文中选用国际MIRA阶梯背标准模型进行研究,MIRA模型作为国际公认的标准模型,在进行基础研究时被广泛使用。其结构较为简单,车身没有复杂附件,底盘简化成为光滑的平板, 如图 1所示。

|
图 1 MIRA模型实体模型图 Figure 1 MIRA Model |
研究表明,气动阻力的产生与边界层厚度有关。由于非光滑表面对于流场的影响主要是在整个附面层内部,因此,非光滑表面尺寸参照车身边界层厚度来选取。平板模型湍流附面层厚度计算公式为δ(l)=0.035l/Re(l)1/7, 式中:δ(l)为附面层厚度;l为平板的长度;Re(l)为雷诺数,为Re(l)=Vl/ν, 来流速度V=40 m/s,运动粘度系数ν=0.072 2 m2/s。可以得出钝体模型车身尾部非光滑单元体的深度最大值为δ(l)=8.06 mm。因此,凹坑型非光滑单元体、凸包型非光滑单元体及沟槽型非光滑单元体的初始深度均设为4 mm。
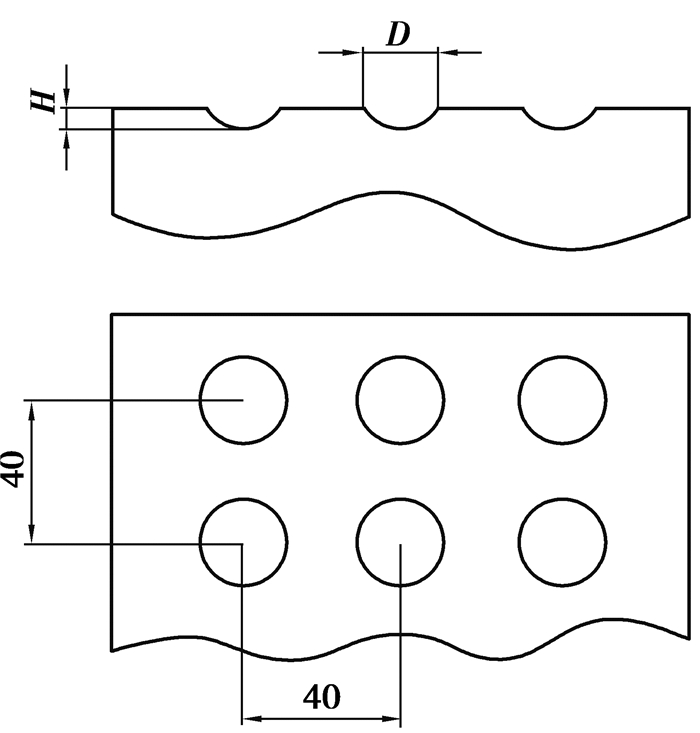
1.1 凹坑型非光滑单元体布置研究表明,矩形排布的非光滑结构减阻效果更为明显。因此,在凹坑单元体选择矩形排布时,凹坑结构为球冠形,其宽度D与深度S之比为1:4,单元体横向间距与纵向间距均为40 mm, 如图 2所示。
|
图 2 凹坑型非光滑单元体尺寸布局图 Figure 2 Pit Non-smooth Layout |
参照凹坑型非光滑单元体,凸包型非光滑单元体也采用矩形排布,结构为球冠形,其宽度D与深度S之比为1:4,单元体横向间距与纵向间距均为40 mm,如图 3所示。

|
图 3 凸包型非光滑单元体尺寸示意图 Figure 3 Convex Non-smooth Layout |
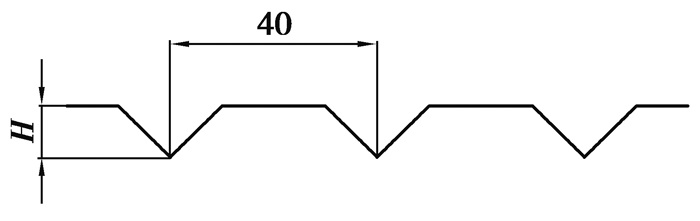
最初的沟槽类型主要包括V型、U型、矩形和三角形等,研究表明,对称V型沟槽具有最好的减阻效果,影响V型沟槽减阻效果的主要因素是排列方式和沟槽尺寸。一般来说,顺流向比垂直流向具有更明显的减阻效果。沟槽尺寸主要是指沟槽的高度和角度,如图 4所示。文中沟槽型非光滑单元体高度为4 mm,间距为40 mm,角度为90°[7]。
|
图 4 沟槽型非光滑单元体尺寸示意图 Figure 4 Groove Non-smooth Layout |
研究所使用的MIRA阶梯背模型在UG中按1:1比例建立,所研究的凹坑型非光滑表面、凸包型非光滑表面和沟槽型非光滑表面也均采用UG建模,如图 5所示。

|
图 5 非光滑单元体三维示意图 Figure 5 3d Model of Non-smooth structure |
数值模拟过程中,足够的流体区域是计算精度的重要保证。为使来流均匀稳定,尾流充分发展以避免产生回流,计算域尺寸如下:车前为3倍车长,车后为7倍车长,车顶上方为5倍车高,车左右均为5倍车宽,计算域的总长46 200 mm,总宽11 200 mm,总高7 000 mm,入口至车前长度12 600 mm,基本消除阻塞效应影响[8]。采用ANSYS-ICEM生成计算域网格,采用非机构化四面体网格划分,整体网格尺寸最大为256 mm,车身表面网格尺寸最大为32 mm,并在模型表面生成三棱柱网格模拟附面层效应,消除壁面函数的影响。同时,为了确保模型周围流场尤其是尾部流场的准确性,对模型周围一定区域内的网格进行加密。
2.3 边界条件设置采用ANSYS-FLUENT软件进行求解,湍流模型采用Realizable k-ε模型,运用二阶迎风格式进行离散求解,残差值设为0.000 001,迭代步数为3 000步,计算域温度设为常温,进行CFD稳态仿真计算,边界条件设置如表 1所示[9-10]。
| 表 1 边界条件设置 Table 1 Boundary Conditions |
将MIRA阶梯背光滑车身模型数值仿真结果与湖南大学风工程试验研究中心HD-2风洞试验已有测试结果进行对比。通过风洞试验测得光滑模型的气动阻力系数CD为0.324 2,通过数值仿真得到模型的气动阻力系数CD为0.317 7,风洞试验结果与仿真结果误差在工程允许误差的5%以内,文中所采用的数值仿真方法具有较高的可靠性。
对凹坑型、凸包型、沟槽型非光滑单元体结构分别进行数值仿真分析,仿真结果如表 2所示。可见,凹坑、凸包和沟槽3种形式的非光滑单元体都产生了显著的减阻效果。
| 表 2 数值仿真结果 Table 2 Numerical Simulation Results |
考虑到实验成本等诸多因素,只采用了凹坑型非光滑单元体结构。实验在湖南大学HD-2风洞实验中进行,将凹坑型非光滑单元体结构薄膜贴于MIRA模型尾部,如图 6所示。实验测定CD值为0.315 3,相比MIRA光滑模型CD值0.324 2,减阻率达到2.75%。同时,凹坑型非光滑单元体结构模型CFD仿真CD值为0.310 5,与试验测定值0.315 3相比,误差仅为1.52%,表明仿真结果精确度较高,仿真与实验结果都表明非光滑单元体结构具有良好的减阻效果。

|
图 6 非光滑模型风洞实验图 Figure 6 Wind Tunnel Test of Non-smooth Model |
非光滑单元体特征参数是影响其减阻效果的主要因素,如果按照传统的设计方法,需要大量的试验来确定合理的参数,但是试验成本高,耗时长[11]。随着计算机技术的快速发展,数值模拟提供了解决问题的方法:采用CFD数值仿真结合参数优化的方法对非光滑单元体特征参数进行优化设计。
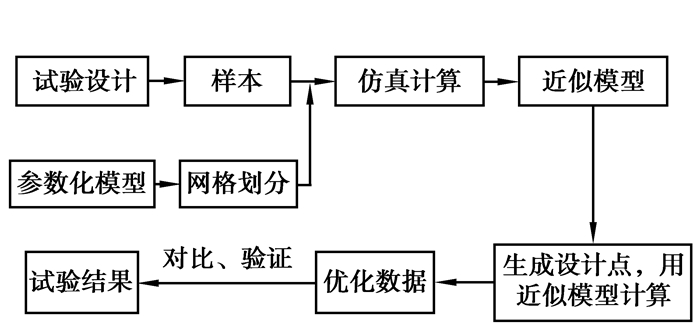
通过试验设计获取样本点,运用UG构建模型,ICEM划分网格,FLUENT求解计算,获得样本点的响应值,并以此构建近似模型,采用基于Pareto概念的带精英策略的非支配排序遗传算法进行优化设计,优化流程如图 7所示。
|
图 7 优化流程图 Figure 7 Optimization Flow Chart |
非光滑单元体结构的特征参数是影响其减阻效果的重要因素,对于文中凹坑型、凸包型和沟槽型非光滑单元体结构,其特征参数主要是指深度H(mm)和间距L(mm)。文中旨在寻求各因素之间的最优组合,以达到最大的减阻效果。优化问题描述如下:
| $\begin{array}{c} \min f = {C_{\rm{D}}};\\ K \in {X_1};\\ L \in {X_2}. \end{array}$ |
式中:f为目标评价函数; H、L分别表示设计变量; X1、X2分别为H和L的设计空间,X1、X2的取值范围分别是[0, 8]和[40, 80]。
3.2 实验设计根据设计变量的取值范围,采用拉丁超立方抽样方法[12-13]选取20组样本点,并分别对凹坑、凸包、沟槽型非光滑单元体结构进行CFD仿真计算,得到相应响应值CD1、CD2、CD3,如表 3所示。
| 表 3 样本点及其响应值 Table 3 Sample Points and Response Value |
根据样本点及其响应值建立设计变量与优化目标之间的Kriging近似模型[14-15],为检验近似模型的拟合精度,对随机五组变量进行验证,如表 4所示。由表可知近似模型与CFD仿真结果的误差都在3%以内,说明近似模型的精度较高,可以替代CFD仿真计算。
| 表 4 近似模型拟合精度检验 Table 4 Accuracy Test of Approximate Model |
采用基于Pareto概念的精英策略非支配排序遗传算法(NSGA-II)[16-19]。作为1994年发布的NSGA的改良版,由K.Deb和S.Agrawal等提出,该算法的准确性和分散性较好,且具有较高的计算效率和算法稳定性。根据Kriging近似模型进行优化,初始种群50个,迭代100代分别得到凹坑、凸包和沟槽非光滑单元体结构的最优解:H1=4.06 mm, L1=60.90 mm,CD1=0.289 0;H2=4.34 mm, L2=61.09 mm, CD2=0.299 7;H3=4.29 mm,L3=61.14 mm,CD3=0.3005。与优化前各非光滑单元体结构模型的CD值对比如表 5所示。可见,优化后模型的减阻效果明显,其中以凹坑型非光滑单元体结构减阻效果最好,达到6.92%。
| 表 5 优化前后阻力系数对比 Table 5 Drag Coefficient Contrast |
对优化后的凹坑、凸包和沟槽型非光滑单元体结构进行数值仿真计算,结果如表 6所示。从表中可以看出,利用Isight软件求得的最优解CD值与优化后CFD仿真CD值的误差均在工程误差允许值3%以内。同时,将优化后的凹坑型非光滑单元体薄膜贴于MIRA阶梯背模型尾部,在湖南大学HD-2风洞实验中进行, 测得该非光滑模型的气动阻力CD值为0.295 3,与优化后仿真CD值0.292 1相比误差为1.10%,与最优解CD值0.289 0相比误差为2.18%,仿真与实验结果均表明优化结果准确可靠。
| 表 6 优化结果验证 Table 6 Validation of Optimization Results |
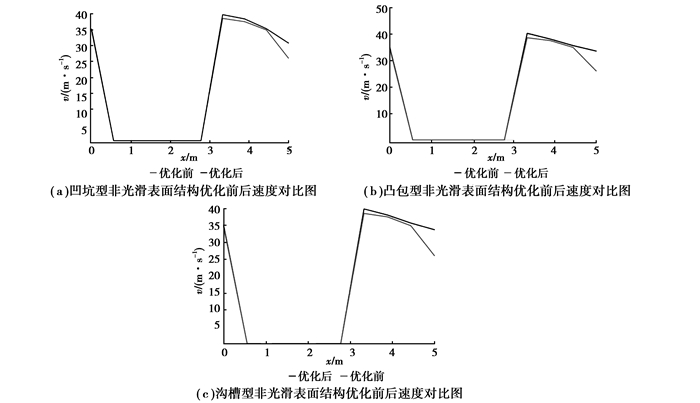
图 8(a)、(b)、(c)分别为凹坑型、凸包型与沟槽型非光滑表面结构优化前后速度对比图。从图中可以看出,优化前后模型前部的气流速度并无明显变化,但靠近模型尾部部分的气流速度明显不同,优化后的气流速度明显要大于优化前的气流速度。气流速度的增加说明凹坑型非光滑单元体改变了模型边界层气流的速度梯度,边界层内外动量交换减弱,动量的传递更加顺畅,从而减少了能量的耗散,减小了模型的气动阻力。
|
图 8 非光滑表面结构优化前后速度对比图 Figure 8 Velocity Contrast of Non-smooth Model before and after Optimization |
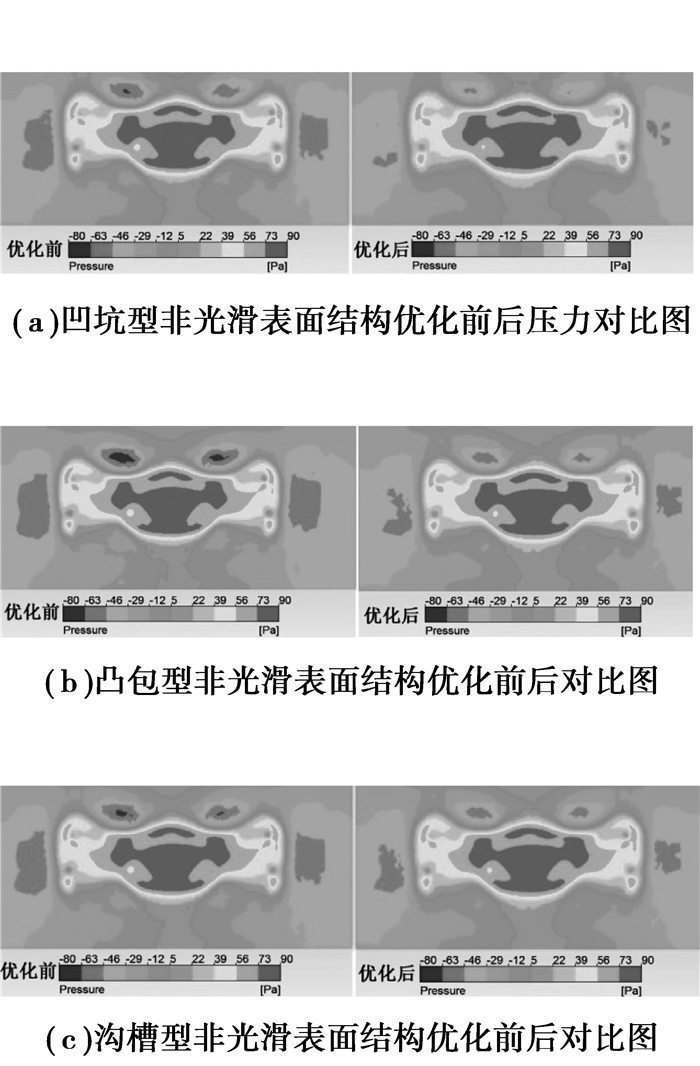
图 9(a)、(b)、(c)分别为凹坑型、凸包型和沟槽型非光滑表面模型优化前后距离尾部250 mm平面上的压力云图。众所周知,压差阻力约占汽车总气动阻力的50%~60%,是气动阻力的主要组成部分,要减小压差阻力,主要是减小汽车前部的正压区和后部的负压区。文中的非光滑单元体结构布置在模型尾部,对其前部的正压区不会产生影响,主要影响的是模型尾部的负压区。从图中可以看出,经过优化,凹坑型、凸包型和沟槽型非光滑单元体结构模型尾部的负压区面积都有所减小,说明尾部压力增大,压差阻力减小,从而减小了模型的气动阻力。
|
图 9 非光滑模型尾部250 mm平面优化前后压力云图 Figure 9 Pressure Contrast at 250 mm Plane away from Non-smooth Model's Rear |
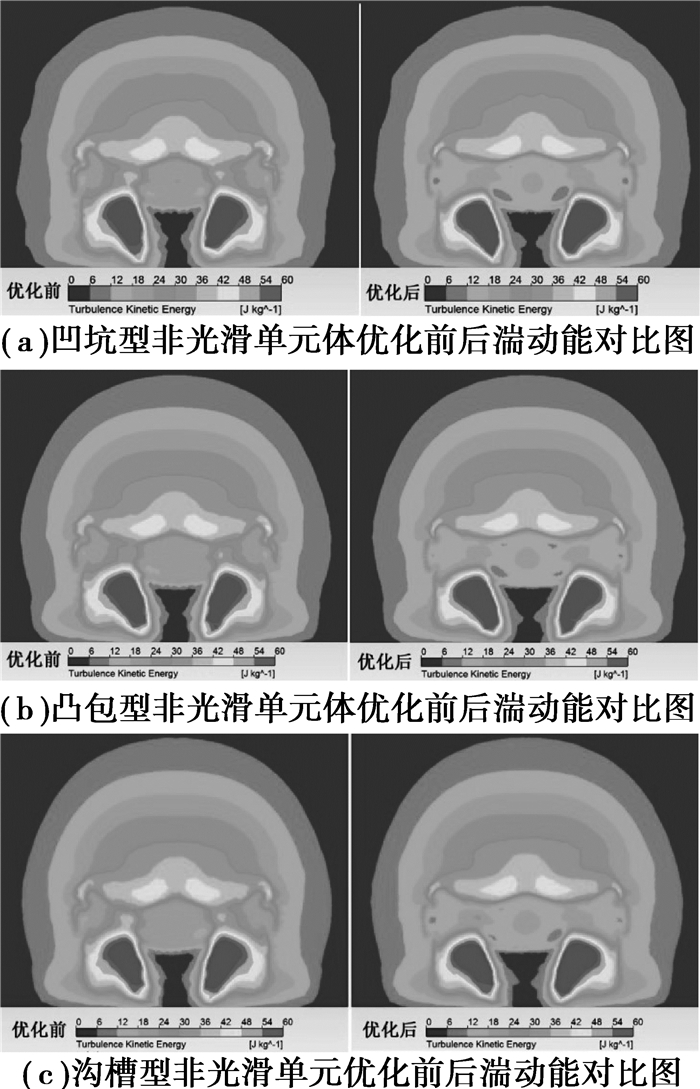
图 10(a)、(b)、(c)为凹坑型、凸包型和沟槽型非光滑表面结构模型尾部250 mm平面优化前后湍动能对比图。从图中可以看出,优化后的湍动能均比优化前有不同程度的减小。湍动能越小,说明气流流过模型时的能量耗散越小,因而优化后的非光滑表面结构模型比优化前的非光滑表面模型的气动阻力要小。
|
图 10 非光滑模型尾部250 mm平面湍动能云图 Figure 10 Turbulent Energy Contrast at 250mm Plane away from Non-smooth Model's Rear |
1) 非光滑单元体结构的特征参数是影响其减阻效果的重要因素,合理布置在MIRA模型尾部的凹坑型、凸包型和沟槽型非光滑单元体结构均能起到一定的气动减阻效果。
2) 布置在MIRA模型尾部的非光滑单元体结构主要影响模型尾部的气流速度和压力,以达到减阻效果,而对模型前部的影响可忽略不计。
3) 采用拉丁超抽样方法进行抽样设计,建立Kringing近似模型并检验近似模型的拟合精度,利用NSGA-II遗传优化算法对布置在MIRA模型尾部的凹坑型、凸包型和沟槽型非光滑单元体结构分别进行优化设计,优化后模型的气动阻力均进一步减小,减阻率分别达到6.92%、4.03%、4.24%。说明该优化设计方法可靠有效,为非光滑单元体结构特征参数的后续设计与研究提供方法参考。
4) 文中只做了凹坑型非光滑单元体结构模型的汽车风洞实验,在后续工作中有待开展不同非光滑表面结构形态模型的风洞实验,结合数值仿真计算方法,寻求更先进有效的优化设计方法。
| [1] |
谷正气. 汽车空气动力学[M]. 北京: 人民交通出版社, 2005.
GU Zhengqi. Automotive aerodynamics[M]. Beijing: China Communications Press, 2005. (in Chinese) |
| [2] |
谌可, 王耘, 曹开元, 等.
仿生非光滑汽车表面的减阻分析[J]. 中国机械工程, 2012(8): 1001–1006.
CHEN Ke, WANG Yun, CAO Kaiyuan, et al. Analysis of Aerodynamic Drag Reduction on Automobile by Using Bionic Non-smooth Surface[J]. China Mechanical Engineering, 2012(8): 1001–1006. (in Chinese) |
| [3] | Dong Y F, Peng S C, Yin X H, et al. Numerical Simulation and Drag Reduction Performance Analysis of Non-smooth Surface with Dimples in Air[J]. Journal of System Simulation, 2014, 26(6): 1191–1196. |
| [4] | Hu Y L, Zhu M L, Xiao J, et al. The Numerical Research of Drag Reduction over Bionic Fluctuation-Adaptive Non-Smooth Surface[J]. Advanced Materials Research, 2014, 939: 499–505. DOI:10.4028/www.scientific.net/AMR.939 |
| [5] | Bixler G D, Bhushan B. Shark skin inspired low-drag microstructured surfaces in closed channel flow[J]. Journal of Colloid and Interface Science, 2013, 393(3): 384–396. |
| [6] |
张成春.旋成体仿生非光滑表面流场控制减阻研究[D].吉林:吉林大学, 2007. ZHANG Chengchun.Drag Reduction of Bodies of Revolution by Flow Control Using Bionic Non-Smooth Surface[D].Jilin: Jilin University, 2007.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10183-2007095701.htm |
| [7] |
李文火.沟槽型非光滑车表汽车气动减阻特性研究[D].杭州:浙江大学, 2014. LI Wenhuo.Study of Aerodynamic Drag Reduction Feature on Automobile with Non-smooth Groove Surface[D].Hangzhou: Zhejiang University, 2014.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10335-1014173211.htm |
| [8] |
庞加斌, 刘晓晖, 陈力, 等.
汽车风洞实验中的雷诺数、阻塞和边界层效应问题综述[J]. 汽车工程, 2009, 31(7): 609–615.
PANG Jiabin, LIU Xiaohui, Chen Li, et al. A review on reynolds number, blockage and boundary layer effects in automotive wind tunnel tests[J]. Automotive Engineering, 2009, 31(7): 609–615. (in Chinese) |
| [9] |
何忆斌, 谷正气, 吴军, 等.
三方程在汽车外流场仿真计算中的应用[J]. 机械工程学报, 2008, 44(1): 184–189.
HE Yibin, GU Zhengqi, WU Jun, et al. Application of Three-equation Turbulence Model in Numerical Simulation of Vehicle External Flow Field[J]. Chinese Journal of Mechanical Engineering, 2008, 44(1): 184–189. DOI:10.3901/JME.2008.01.184 (in Chinese) |
| [10] |
谷正气, 姜乐华, 吴军, 等.
汽车绕流的数值分析及计算机模拟[J]. 空气动力学学报, 2000, 18(2): 3–4.
GU Zhengqi, JIANG Lehua, WU Jun, et al. The Numerical Analysis and Computer Simulation on Automobile Flowfield[J]. Acta Aerodynamica Sinica, 2000, 18(2): 3–4. (in Chinese) |
| [11] | Lietz R L.Vehicle aerodynamic shape optimization[C]//SAE paper 2011-01-0169.Chemical Engineering Science, 2004, 59:385-396. |
| [12] |
陈魁. 实验设计与分析[M]. 北京: 清华大学出版社, 2005: 97-100.
CHEN Kui. Design and Analysis of Experiment[M]. Beijing: Tsinghua University Press, 2005: 97-100. (in Chinese) |
| [13] | Park J, Lee K S, Kim M S, et al. Numerical analysis of a dual-fueled CI (compression ignition) engine using Latin hypercube sampling and multi-objective Pareto optimization[J]. Energy, 2014, 70(1): 278–287. |
| [14] | Soren N Lophaven, HansBruun Nielsen, Jacbo Sondergaard.DACE a matlab kriging toolbox[R].Technical Report.IMM-TR-2002-12, Denmark: Technical University of Denmark, 2002. |
| [15] | Li Y, Wu Y, Huang Z. An incremental kriging method for sequential optimal experimental design[J]. CMES: Computer Modeling in Engineering & Sciences, 2014, 97(4): 323–357. |
| [16] | Deb K, Agrawal S, Pratap A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-Ⅱ[J]. Lecture notes in computer science, 2000, 1917: 849–858. DOI:10.1007/3-540-45356-3 |
| [17] | Ippolito M G, Di Silvestre M L, Sanseverino E R, et al. Multi-objective optimized management of electrical energy storage systems in an islanded network with renewable energy sources under different design scenarios[J]. Energy, 2014, 64: 648–662. DOI:10.1016/j.energy.2013.11.065 |
| [18] | Chen H, Ooka R, Kato S. Study on optimum design method for pleasant outdoor thermal environment using genetic algorithms (GA) and coupled simulation of convection, radiation and conduction[J]. Building and Environment, 2008, 43(1): 18–30. DOI:10.1016/j.buildenv.2006.11.039 |
| [19] | Queipo N V, Haftka R T, Shyy W, et al. Surrogate-based analysis and optimization[J]. Aerospace Sciences, 2005, 41: 1–28. DOI:10.1016/j.paerosci.2005.02.001 |
 2015, Vol. 38
2015, Vol. 38

