由于内嵌管式辐射地板的传热是多维动态的, 加之形状不够规则, 很难通过解析方法求解其传热问题。目前已存在许多半解析模型[1-4], 但大部分模型都只能进行稳态求解[5]。关于内嵌管式辐射地板的动态传热模拟更多的是采用数值模型[6-7]。数值模型的精度取决于模型的阶数(划分网格单元的数量), 通常可以通过加密网格的方式获得足够准确的计算结果。以上关于内嵌管式辐射地板的传热研究都是在时间域里进行的, 目前关于内嵌管式辐射地板的频域传热特性的研究较少。建筑的传热过程呈现明显的周期型特征, 比如1天(24 h)为周期、1年(8 760 h)为周期等, 建筑的传热(假设其为线性系统)可以看成是不同周期谐波热扰作用效果的叠加[8]。在进行短周期的建筑传热计算模拟时, 时域数值方法可以很快地获得计算结果, 然而对于较长周期的计算模拟, 采用时域数值方法进行模拟并达到准稳定状态, 其计算量非常大, 这是由于时域数值方法通常需要给定计算域的初始值, 并通过数个周期的计算才能达到准稳态。与时域数值方法不同的是, 频域数值方法不需要初始值的设定也不需要进行数个周期的模拟而可以直接得出准确稳态下的计算结果。
有限元法结合了经典变分理论和有限差分法中的离散处理的特点, 克服了有限差分法只注重节点的作用而忽视单元本身特性的这一不足。以各单元的节点温度为基本的未知量, 将单元内的温度分布表示成关于节点温度的插值函数, 采用变分原理建立关于各个单元的节点温度的方程, 最后再合成为整体求解区域的有限元法方程组进行求解, 这就是有限元法的基本求解思路。相比于有限差分法, 有限元法具有任意布置节点和网格的特点, 在不规则结构的传热问题求解时表现出较大的适应性和灵活性[9]。
文中采用频域有限元法建立内嵌管式辐射地板的频域有限元模型以进行内嵌管式辐射地板的频域热特性分析。进一步采用ANSYS建立了该结构的热特性模型, 该模型的结果作为参考值用以评估该结构的频域有限元模型的计算结果的准确性。
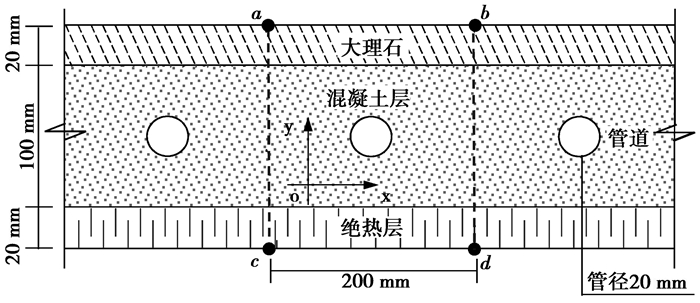
1 内嵌管式辐射地板物理模型简化选取的内嵌管式辐射地板的结构如图 1所示, 地板材料的热物性参数如表 1所示。根据内嵌管式辐射地板的结构特征, 可以取图 1中abcd部分所示的基本结构单元为研究对象。忽略沿管道方向水温的变化(一般沿管道方向的水温变化较小), 即将模型简化为二维模型, 忽略管壁的导热热阻, 不考虑水与管道内壁面的对流换热, 直接假设管道外壁面的温度等于管道中的水温。
|
图 1 内嵌管式辐射地板的结构示意图 Figure 1 Schematic diagram of pipe-embedded radiant floor |
| 表 1 内嵌管式辐射地板的热物性参数 Table 1 Thermo-physical parameters of pipe-embedded radiant floor |
内嵌管式辐射地板的二维导热微分方程如式(1)所示:
| $k\left( {\frac{{{\partial ^2}T}}{{\partial {x^2}}} + \frac{{{\partial ^2}T}}{{\partial {y^2}}}} \right) + {q_v}-\rho c\frac{{\partial T}}{{\partial t}} = 0, $ | (1) |
其中:T为温度变量, ℃; t为时间变量, s; qv为内热源, W/m2; ρ为密度, kg/m3; c为比热, J/kg·K。任意周期性变化的温度波都可以通过傅里叶变换展开成不同频率的温度谐波的叠加, 如式(2)所示。根据线性系统叠加性原理, 内嵌管式辐射地板的传热可以看成是由有限个温度谐波作用效果的叠加。对单一温度谐波作用的情况进行研究。温度变量如式(3)所示, 温度关于时间的导数如式(4)所示。将温度的复指数表达式(4)代入到式(1)中可以得式(5)。
| $T = \bar T + \sum\limits_{j = 1}^N {{{\hat T}_j}{{\rm{e}}^{\hat i\left( {\omega jt + \tilde \omega j} \right)}}, } $ | (2) |
| $T = \hat T{{\rm{e}}^{\hat i\left( {\omega t + \tilde \omega } \right)}} = \left( {u + \hat iv} \right){{\rm{e}}^{\hat i\omega t}}, $ | (3) |
| $\frac{{\partial T}}{{\partial t}} = \hat i\omega \hat T{{\rm{e}}^{\hat i\left( {\omega t + \tilde \omega } \right)}} = \left( {u + \hat iv} \right){{\rm{e}}^{\hat i\omega t}}, $ | (4) |
| $k\left( {\frac{{{\partial ^2}T}}{{\partial {x^2}}} + \frac{{{\partial ^2}T}}{{\partial {y^2}}}} \right) + {q_v}-\rho c\hat i\omega T = 0, $ | (5) |
其中:T为平均温度, ℃;
采用Galerkin法[9]推导得内嵌管式辐射地板平面温度场的频域有限单元法计算的基本方程, 如式(6)所示。该式可采用3种边界条件, 即第一类边界条件如式(7), 第二类边界条件如式(8), 第三类边界条件如式(9)。
| $\begin{array}{c} \frac{{\partial {J^D}}}{{\partial {T_l}}} = \mathop {\smallint \smallint }\limits_D \left[{k\left( {\frac{{\partial {W_l}}}{{\partial x}}\frac{{\partial T}}{{\partial x}} + \frac{{\partial {W_l}}}{{\partial y}}\frac{{\partial T}}{{\partial y}}} \right)-{q_v}{W_l} + \rho c{W_l}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} \omega T} \right]{\rm{d}}x{\rm{d}}y -\\ \oint\limits_\mathit{\Gamma } {{W_l}k\frac{{\partial T}}{{\partial n}}{\rm{d}}s} = 0\;\;\;\left( {l = 1, 2, \cdots, n} \right), \end{array}$ | (6) |
| $\oint\limits_\mathit{\Gamma } {{W_l}k\frac{{\partial T}}{{\partial n}}{\rm{d}}s = 0, } $ | (7) |
| $\oint\limits_\mathit{\Gamma } {{W_l}k\frac{{\partial T}}{{\partial n}}{\rm{d}}s} =-\oint\limits_\mathit{\Gamma } {{W_l}q{\rm{d}}s}, $ | (8) |
| $\oint\limits_\mathit{\Gamma } {{W_l}k\frac{{\partial T}}{{\partial n}}{\rm{d}}s} =-\oint\limits_\mathit{\Gamma } {{W_l}\alpha \left( {T-{T_f}} \right){\rm{d}}s}, $ | (9) |
其中:Wl为加权函数
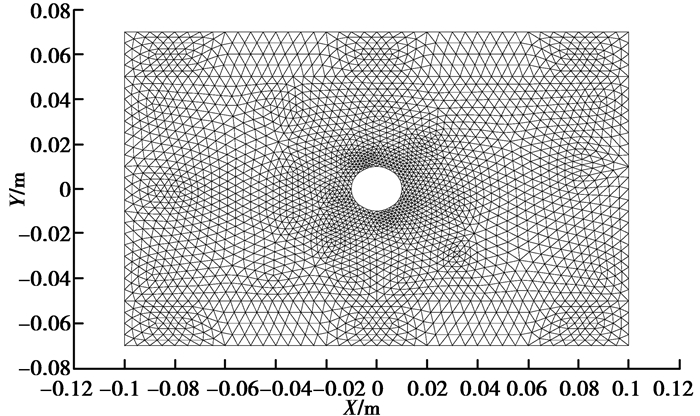
将区域D(即图 1所示的结构abcd)划分成E个单元和n个结点, 划分网格如图(2)所示。网格数量E为5 280, 节点数n为2 724。将温度场离散成T1, T2, …, Tn等n个结点的待定温度值, 这时对任意单元的变分计算如式(10)所示, 进一步可以得到总的合成方程组, 如式(11)所示。将单元的温度T的关于x, y的线性插值函数以及各结点的坐标值代入到总的合成方程(11)中, 就可以计算得到关于n个节点温度的代数方程组, 并写成矩阵形式, 如方程组(12)所示。方程(12)中的T项和
| $\begin{array}{c} \frac{{\partial {J^e}}}{{\partial {T_l}}} = \mathop {\smallint \smallint }\limits_e \left[{k\left( {\frac{{\partial {W_l}}}{{\partial x}}\frac{{\partial T}}{{\partial x}} + \frac{{\partial {W_l}}}{{\partial y}}\frac{{\partial T}}{{\partial y}}} \right)-{q_v}{W_l} + \rho c{W_l}{\rm{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }}\omega T} \right]{\rm{d}}x{\rm{d}}y -\\ \int\limits_{{\mathit{\Gamma }_e}} {{W_l}k\frac{{\partial T}}{{\partial n}}{\rm{d}}s} = 0\;\;\left( {l = i, j, m} \right), \end{array}$ | (10) |
| $\frac{{\partial {J^D}}}{{\partial {T_l}}} = \sum\limits_{e = 1}^E {\frac{{\partial {J^e}}}{{\partial {T_l}}} = 0\;\left( {l = 1, 2, 3 \cdots, n} \right), } $ | (11) |
| $\left[\boldsymbol{K} \right]\left\{ T \right\} + \left[\boldsymbol{N} \right]\left\{ {\partial T/\partial t} \right\} = \left\{ \boldsymbol{P} \right\}, $ | (12) |
| $\left[\boldsymbol{K} \right]\left\{ {u + {\rm{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} }}v} \right\} + \omega \left[\boldsymbol{N} \right]\left\{ { -v + {\rm{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over i} u}}} \right\} = 0, $ | (13) |
其中:矩阵[K]为温度的刚度矩阵;[N]为非稳态变温矩阵(热容矩阵);{P}为等式右端项组成的列向量, 内嵌管式辐射地板一般无内热源, 因此此项通常为0向量。
|
图 2 内嵌管式辐射地板结构的有限元网格划分 Figure 2 Meshing of the pipe-embedded radiant floor by using FEM |
对方程(13)进行求解就可以得到在任意频率ω下各个节点的频域温度响应(即各点频率相同、振幅和相位不同的温度谐波)。
3 特征热扰由文献[8]中关于板壁频域热响应的计算分析可知, 对于线性导热问题, 频域热响应(板壁对温度谐波热扰的衰减和时间延迟或者相角差)与温度谐波热扰的幅值和相角均无关。内嵌管式辐射地板的导热微分方程为线性方程, 地板各表面的频域热流响应的幅值与温度谐波热扰的幅值呈线性比例关系(该比例只与频率和该结构的热物性有关), 两者的相角差与温度谐波热扰的相角无关, 为了便于分析, 在计算内嵌管式辐射地板频域热流响应时, 温度谐波热扰均采用相角为0的单位温度谐波。内嵌管式辐射地板同时受到3个边界热扰(地板上表面、地板下表面以及管道表面)的作用, 特将其受到的热扰情况设置成3种特征热扰:1)地板上表面特征热扰, 即上表面受到频率为ω、幅值为1、相角为0的温度谐波扰动, 地板下表面和管道表面的热扰均为0;2)地板下表面特征热扰, 即地板下表面受到频率为ω、幅值为1、相角为0的温度谐波扰动, 地板上表面和管道表面的热扰均为0;3)管道表面特征热扰, 即管道表面受到频率为ω、幅值为1、相角为0的温度谐波扰动, 地板上表面和地板下表面的热扰均为0。由于地板下表面的温度波动一般较小, 加之地板绝热层对地板下表面的热扰向地板传递具有明显的抵抗作用, 因此文中只针对上表面特征热扰和管道表面特征热扰这2种情况进行研究分析。
4 ANSYS参考模型采用实验来验证理论研究结果往往需要消耗较多的人力、物力和时间成本, 随着计算机技术和数值计算理论的发展, 计算机数值模拟技术日趋成熟, 目前已有很多研究开始在实验条件不具备的情况下采用ANSYS软件搭建数值模拟的虚拟实验平台替代真实实验来对理论研究结果进行初步验证[10-11]。为了说明内嵌管式辐射地板频域有限元模型的准确性, 采用ANSYS软件建立了该结构的时域传热模型(即ANSYS模型)作为参考模型。给定ANSYS模型相应的边界条件(特征热扰), 热扰温度以正弦函数的形式给定, 对于任意频率ω, 热扰温度的周期为2π/ω。由于ANSYS模型无法直接计算得到内嵌管式辐射地板传热的准稳态计算结果, 因此需要进行多个周期的计算模拟直到前后2个周期的计算结果几乎没有差别为止(即达到准稳态)。由ANSYS模型的计算结果可以进一步得到频率为ω的单位谐波作用下地板各表面准稳态热流响应。
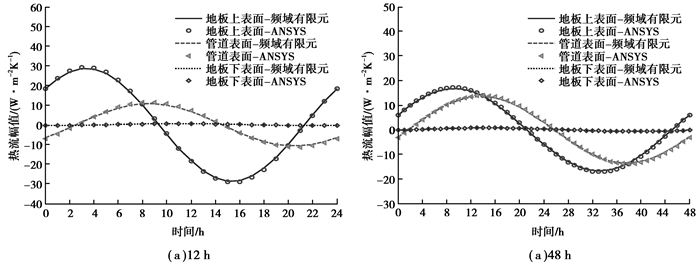
5 频域有限元模型准确性分析频域有限元模型和ANSYS模型均可以得到频率为ω的单位谐波作用下地板各表面准稳态热流响应, 通过将2个模型在一系列频率点(周期)的计算结果进行对比可以说明频域有限元模型的准确性。频域有限元模型可以得到地板各表面的热流谐波函数, 如式(14)所示。根据式(15)可以得到热流谐波函数的幅值q和相角φ。ANSYS计算结果为各个时间点上的地板各表面离散热流值。限于篇幅, 选取这2个模型在周期为12 h (对应的频率为1.45×10-4 rad/s)和48 h (对应的频率为3.64×10-5 rad/s)的计算结果进行比较。比较结果如图 3所示。
| $q = \hat q{{\rm{e}}^{\hat i\left( {\omega t + \tilde \omega } \right)}} = \left( {u + \hat iv} \right){{\rm{e}}^{\hat i\omega t}} = \bar q\sin \left( {\omega t + \tilde \omega } \right), $ | (14) |
| $\bar q = \sqrt {{u^2} + {v^2}}, \varphi = {\rm{atan}}\left( {v/u} \right).$ | (15) |
|
图 3 频域有限元模型与ANSYS模型(时域有限元模型)计算结果的对比 Figure 3 Comparison of the results calculated by Frequency-Domain Finite Element Model and ANSYS model (i.e. Time-Domain Finite Element Model) |
结果对比表明,内嵌管式辐射地板频域有限元模型和ANSYS模型计算结果吻合得非常好, 最大相对偏差为3%, 平均相对偏差为1.8%。说明2个模型都可以很准确地计算内嵌管式辐射地板的热特性, 采用频域有限元模型计算内嵌管式辐射地板的频域热特性是可靠的。
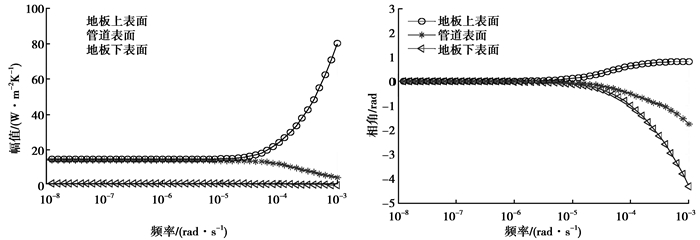
6 内嵌管式辐射地板频域热特性分析采用内嵌管式辐射地板的频域有限元模型计算该结构在不同频率的特征热扰作用下的各表面热流响应, 所选的频率范围为:10-8rad/s (周期19.8年)~10-3rad/s (周期1.74 h)[12]。图 4和图 5分别为地板上表面特征热扰和管道表面特征热扰作用下地板各表面的频域热流响应。
|
图 4 地板上表面特征热扰下地板各表面的频域热流响应 Figure 4 Frequency heat flux responses on different surfaces to the upper floor surface characteristic disturbance |

|
图 5 管道表面特征热扰下地板各表面的频域热流响应 Figure 5 Frequency heat flux responses on different surfaces to the pipe surface characteristic disturbance |
图 3和图 4的结果显示在低频区域内嵌管式辐射地板各表面的热流响应几乎不随频率变化, 且相角均接近于0, 说明在低频区域, 内嵌管式辐射地板的传热几乎不存在延迟, 接近于稳态传热, 且热流幅值基本不变。在高频区域内嵌管式辐射地板各表面的热流响应变化比较剧烈, 相位的延迟明显, 热流幅值变化明显。说明在高频区域内嵌管式辐射地板传热的动态特征非常明显, 地板中存在比较明显的蓄热过程, 这与地板自身材料的高蓄热特性相吻合。在实际的内嵌管式地板辐射系统中, 由于水温的波动以及房间内热扰波动(人员散热等)存在较多的高频成分, 如果采用稳态方法计算内嵌管式辐射地板的传热会造成较大的偏差, 因此在计算内嵌管式辐射地板的传热时, 应采用动态计算方法。
7 结论建立了内嵌管式辐射地板的频域有限元模型, 计算并分析了内嵌管式辐射地板的频域热特性。
1) 采用ANSYS软件建立了该结构的时域传热模型, 对比发现2个模型计算的地板各表面准稳态热流响应吻合得非常好,最大相对偏差为3%, 平均相对偏差为1.8%, 说明了文中建立的内嵌管式辐射地板的频域有限元模型具有较好的准确性且相关建模方法是合理的。
2) 在低频区域(频率低于5.0×10-5 rad/s, 周期大于34.9 h)内嵌管式辐射地板的频域热流响应基本不随频率变化,相位延迟保持为0,传热接近于稳态传热,在高频区域(频率高于5.0×10-5 rad/s, 即周期小于34.9 h)该结构的频域热流响应随频率的变化剧烈变化,在房间热扰波动具有较多的高频成分时,应采用动态计算方法来计算内嵌管式辐射地板的传热。
| [1] |
王立, 吴南路.
地板辐射供暖系统传热的简化解析计算[J]. 哈尔滨商业大学学报(自然科学版), 2003, 19(3): 347–349.
WANG Li, WU Nanlu. Study on simplified analytical calculation for heat transfer of floor panel heating system[J]. Journal of Harbin University of Commerce Natural (Sciences Edition), 2003, 19(3): 347–349. (in Chinese) |
| [2] |
胡孟娣, 彭钦磊.
内嵌管式辐射地板传热简化模型研究[J]. 建筑科学, 2012, 28(6): 106–109.
HU Mengdi, PENG Qinlei. Development of simplified thermal model of pipe-embedded radiant floors[J]. Building Science, 2012, 28(6): 106–109. (in Chinese) |
| [3] | ZHANG Z, PATE M B.A semi-analytical formulation for heat transfer from structures with embedded tubes[C].In: The 24th National Heat Transfer Conference, ASME-HTD, vol.78, Pittsburgh, Pennsylvania, August 9-12, 1987, 17-25. |
| [4] |
张伦, 刘晓华, 高志宏, 等.
辐射地板供冷量及表面温度分布的简化计算方法[J]. 暖通空调, 2012, 42(5): 41–46.
ZHANG Lun, LIU Xiaohua, GAO Zhihong, et al. Simplified calculation method for the cooling capacity and surface temperature distribution of floor panel[J]. Heating Ventilating and Air Conditioning, 2012, 42(5): 41–46. (in Chinese) |
| [5] |
徐新华, 谭蓉, 朱求源.
主动式利用低品位能的内嵌管道式建筑结构的传热模型研究进展[J]. 建筑科学, 2009, 25(12): 101–105.
XU Xinhua, TAN Rong, ZHU Qiuyuan. Research progress of thermal modeling of active pipe-embedded building structures for utilizing low-grade energy sources[J]. Building Science, 2009, 25(12): 101–105. (in Chinese) |
| [6] | Wang D, Liu Y, Wang Y, et al. Numerical and experimental analysis of floor heat storage and release during an intermittent in-slab floor heating process[J]. Applied Thermal Engineering, 2014, 62(2): 398–406. DOI:10.1016/j.applthermaleng.2013.09.028 |
| [7] | Jin X, Zhang X, Luo Y, et al. Numerical simulation of radiant floor cooling system: The effects of thermal resistance of pipe and water velocity on the performance[J]. Building & Environment, 2010, 45(11): 2545–2552. |
| [8] |
彦启森, 赵庆珠. 建筑热过程[M]. 北京: 中国建筑工业出版社, 1996: 57-63.
YAN Qiseng, ZHAO Qingzhu. Thernal process in buildings[M]. Beijing: China Architecture and Building Press, 1996: 57-63. (in Chinese) |
| [9] |
孔祥谦. 有限单元法在传热学中的应用[M]. 北京: 科学出版社, 1998.
KONG Xiangqian. The finite element method in heat transfer[M]. Beijing: Science Press, 1998. (in Chinese) |
| [10] |
谭伟, 闫增峰, 孙立新, 等.
利用ANSYS计算异型围护结构中的热桥线传热系数[J]. 建筑科学, 2008, 24(4): 62–66.
TAN Wei, YAN Zengfeng, SUN Lixin, et al. Calculation on linear heat transfer coefficient of thermal bridges in special shape building envelope by ANSYS[J]. Building Science, 2008, 24(4): 62–66. (in Chinese) |
| [11] |
袁艳平, 程宝义, 茅靳丰, 等.
ANSYS在浅埋工程围护结构传热模拟中的运用[J]. 解放军理工大学学报(自然科学版), 2004, 5(2): 52–56.
YUAN Yanping, Cheng Baoyi, Mao Jinfeng, et al. Application of ANSYS in simulation of heat transfer of shallow buried underground engineering[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2004, 5(2): 52–56. (in Chinese) |
| [12] | Wang S, Chen Y. Transient heat flow calculation for multilayer constructions using a frequency-domain regression method[J]. Building and Environment, 2003, 38(2): 45–61. |
 2015, Vol. 38
2015, Vol. 38


