2. 东南大学 交通学院,南京 210018
2. Transportation College, Southeast Universtiy, Nanjing 210018 P.R.China
预应力FRP (fiber reinforced polymer,FRP)增强混凝土结构技术具有显著的优点:限制被加固构件裂缝宽度,延缓构件开裂,增大被加固构件的刚度,改善正常使用性能[1-12]。预应力的施加方法有3种,即反拱法、先张法和后张法[13]。反拱法有效预应力较低,且对被加固构件的力学性能要求较高,因此很难在实际工程中推广应用。先张法设备相对复杂,需要有专门的抬升和张拉装置。后张法是将张拉和锚固装置锚固在被加固构件上,张拉FRP后,使用环氧树脂粘结在被加固构件表面上的一种方法。
一些学者采用后张法技术对预应力CFRP (carbon fiber reinforced polymer)加固混凝土梁的抗弯性能进行了研究,其中一项重要的研究内容是观测预应力损失。El-Hacha等进行了9根后张预应力碳纤维布加固T型预应力混凝土梁短期和长期的预应力损失试验。由于试验梁混凝土的养护龄期较短,且作用有外加的持续荷载,观测到短期预应力损失大约为CFRP布极限强度的16%,而长期预应力损失为CFRP布极限强度的11.3%[14]。Diab等[15]对锚固区的应力分布进行了短期和长期的观测,发现胶层的徐变显著影响锚固长度,是FRP-混凝土界面剥离的主要原因。Kim等[16]考虑界面针对后张法CFRP补强预应力混凝土梁的短期预应力损失,提出了一个闭合解。经过计算,发现短期预应力损失大约为初始应力的10%。
预应力损失可以分为瞬时损失和时间依存损失。瞬时损失[2]是指后张法预应力FRP放张后即刻产生的损失,可以分为预应力FRP回缩引起的损失(锚固损失σA)及预应力FRP合力作用点处混凝土弹性压缩引起的损失σES。在时间依存损失中,混凝土的收缩徐变引起的损失是相互影响的。对于预应力FRP加固的钢筋混凝土梁,胶层的徐变及界面的滑移将进一步增大预应力损失。文中考虑胶层的徐变、界面的滑移及混凝土收缩徐变的相互影响,建立了预应力FRP加固钢筋混凝土梁预应力长期损失的增量微分法,将计算结果与试验结果进行了比较分析。
1 分析模型时间依存损失是指后张法预应力FRP放张后随时间增加的损失,包括预应力FRP应力松弛引起的损失和混凝土收缩徐变引起的损失。
1.1 FRP松弛引起的损失σR该项预应力损失可下式计算[2]:
| $ {\sigma _R} = \frac{{1 - \beta }}{{100}}{f_{{\rm{pi}}}}, $ | (1) |
| $ \beta = 0.275\frac{{{f_{{\rm{pi}}}}}}{{{f_{\rm{u}}}}} - 0.083, $ | (2) |
式中:fpi为FRP初始预应力;fu为FRP极限抗拉强度。
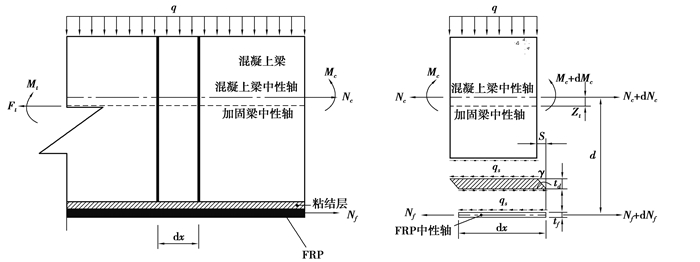
1.2 混凝土收缩徐变及胶层徐变引起的损失σCR在计算混凝土收缩徐变及胶层徐变引起的预应力损失时,可以认为钢筋混凝土梁是未开裂构件,如图 1所示。图 1中各项符号的下角标是一种通用表示方法,即“c”、“f”、“s”分别表示混凝土、FRP和界面剪应力。文中后面各节中公式下角标“t”、“tn-1”、“tn”分别表示t、tn-1、tn时刻。在任意时刻t时,根据截面内外力及微元体平衡可得:
|
图 1 预应力FRP加固混凝土内外力作用及微元体 Figure 1 External and internal forces on the infinitesimal element of prestressed FRP-strengthened beam |
| $ {M_t} = {M_{{\rm{ct}}}} - {N_{{\rm{ct}}}}d + {F_t}\left( {d - z} \right), $ | (3) |
| $ {F_t} = {N_{{\rm{ct}}}} + {N_{{\rm{ft}}}}, $ | (4) |
| $ N{'_{{\rm{ct}}}} = - {K_t}{s_t}, $ | (5) |
| $ {s_t} = {u_{{\rm{ft}}}} - {u_{{\rm{ct}}}} + w{'_t}d, $ | (6) |
式中:Mt为t时刻作用在截面上的外弯矩;Mct为t时刻作用在截面混凝土部分的弯矩;Nct为t时刻作用在截面混凝土部分的轴向力;Ft为t时刻作用在加固梁组合截面上的预应力;d为截面混凝土中性轴至FRP中性轴之间的距离;z为截面混凝土中性轴至加固梁组合截面中性轴距离;Kt是t时刻胶层的剪切刚度;st、uct、uft、wt分别是t时刻FRP-混凝土界面滑移、截面上混凝土部分轴向位移、截面上FRP部分轴向位移及加固梁竖向挠度。
将方程(3)~(6)改写为关于某一时间段[Δtn=tn-tn-1]内的增量形式:
| $ \Delta {M_n} = \Delta {M_{{\rm{c}}n}} - \Delta {N_{{\rm{c}}n}}d + \Delta {F_n}(d - z), $ | (7) |
| $ \Delta {F_n} = \Delta {N_{{\rm{c}}n}} + \Delta {N_{{\rm{f}}n}}, $ | (8) |
| $ \Delta N{'_{{\rm{c}}n}} = - {K_{{{\rm{t}}_{n - 1}}}}\Delta {s_n}, $ | (9) |
| $ \Delta {s_n} = \Delta {u_{{\rm{f}}n}} - \Delta {u_{{\rm{c}}n}} + \left( {\Delta {w_n}} \right)'d, $ | (10) |
| $ z = \frac{{{E_{\rm{f}}}{A_{\rm{f}}}}}{{E{A_0}}}d, $ | (11) |
式中:Af为FRP截面面积;EA0=Ec, tnAc·EfAf;Ec, tn是tn时刻混凝土有效弹性模量;Ef为FRP的弹性模量;Ac是混凝土截面面积;ΔMn为Δtn内外弯矩的增量,ΔMn=Mtn-Mtn-1;ΔMcn为作用在截面上混凝土部分弯矩增量,ΔMcn=Mc, tn-Mc, tn-1;ΔNcn为作用在截面上混凝土部分轴向力增量,ΔNcn=Nc, tn-Nc, tn-1;ΔNfn为作用在截面上FRP部分轴向力增量,ΔNfn=Nf, tn-Nf, tn-1;ΔFn为预应力增量;ΔSn为FRP-混凝土界面滑移增量;Δucn为截面上混凝土部分轴向位移增量;Δufn为截面上FRP部分轴向位移增量;Δwn为加固梁竖向挠度增量;Ktn-1为tn-1时刻胶层的剪切刚度。
在tn时刻,加固梁竖向挠度wtn与截面混凝土部分弯矩Mc, tn的关系为
| $ w'{'_{tn}} = - \frac{{{M_{{\rm{c}},{t_n}}}}}{{{E_{{\rm{c}},{t_n}}}{I_c}}} = - \frac{{{M_{{\rm{c}},{t_{n - 1}}}}}}{{{E_{{\rm{c}},{t_n}}}{I_c}}} - \frac{{\Delta {M_{{\rm{c}}n}}}}{{{E_{{\rm{c}},{t_n}}}{I_c}}}, $ | (12) |
式中:Ic为混凝土部分截面惯性矩;Mc, tn-1为tn-1时刻作用在截面上混凝土部分的弯矩;tn时刻混凝土的弹性模量可以采用有效模量法计算
| $ {E_{{\rm{c}},{t_n}}} = \frac{{{E_{{\rm{c}},{t_{n - 1}}}}}}{{1 + \chi \left( {{t_0},{t_n}} \right) \cdot \varphi \left( {{t_{n - 1}},{t_n}} \right)}}, $ | (13) |
| $ {E_{{\rm{c}},{t_n}}} = \frac{{{E_{{\rm{c}},{{\rm{t}}_0}}}}}{{1 + \chi \left( {{t_0},{t_n}} \right) \cdot \varphi \left( {{t_0},{t_n}} \right)}}, $ | (14) |
式中:Ec, t0为混凝土的初始弹性模量,即t0时刻的弹性模量;Ec, tn-1为tn-1时刻混凝土弹性模量;χ(tn-1, tn)为Δtn时间段内混凝土的老化系数,按照式(15)计算;φ(tn-1, tn)为Δtn时间段内混凝土的徐变系数,φ(tn-1, tn)=φ(t0, tn)-φ(t0, tn-1);φ(t0, tn)、φ(t0, tn-1)分别为tn、tn-1时刻混凝土的徐变系数;t0为考虑混凝土徐变时的混凝土龄期。
应用Dischinger方法[17],老化系数χ(tn-1, tn)为
| $ \chi \left( {{t_{n - 1}},{t_n}} \right) = \frac{1}{{1 - {e^{\varphi \left( {{t_{n - 1}},{t_n}} \right)}}}} - \frac{1}{{\varphi \left( {{t_{n - 1}},{t_n}} \right)}}, $ | (15) |
将式(13)和式(15)代入式(12),并注意到w″tn=w″tn-1+Δw″n,w″tn-1=
| $ \Delta w'{'_n} = - \frac{{{M_{{\rm{c}},{t_{n - 1}}}}\chi \left( {{t_{n - 1}},{t_n}} \right) \cdot \varphi \left( {{t_{n - 1}},{t_n}} \right)}}{{{E_{{\rm{c}},{t_{n - 1}}}}{I_c}}} - \frac{{\Delta {M_{{\rm{c}}n}}}}{{{E_{{\rm{c}},{t_n}}}{I_c}}}, $ | (16) |
联立式(7)和(16)可得:
| $ \Delta w'{'_n} = \frac{{\Delta {M_n} - \Delta {F_n}\left( {d - z} \right) + \Delta {N_{{\rm{c}}n}}d + {M_{{\rm{c}},{t_{n - 1}}}}\frac{{\chi \left( {{t_{n - 1}},{t_n}} \right) \cdot \varphi \left( {{t_{n - 1}},{t_n}} \right)}}{{1 + \chi \left( {{t_{n - 1}},{t_n}} \right) \cdot \varphi \left( {{t_{n - 1}},{t_n}} \right)}}}}{{{E_{{\rm{c}},{t_{n - 1}}}}{I_c}}}, $ | (17) |
对式(10)微分一次,可得:
| $ \Delta s{'_n} = \Delta u{'_{{\rm{f}}n}} - \Delta u{'_{{\rm{c}}n}} + \Delta w'{'_n}d, $ | (18) |
| $ \Delta u{'_{{\rm{f}}n}} = {\varepsilon _{{\rm{f}},{t_n}}} - {\varepsilon _{{\rm{f}},{t_{n - 1}}}} = \frac{{\Delta {N_{{\rm{f}}n}}}}{{{E_{\rm{f}}}{A_{\rm{f}}}}}, $ | (19) |
式中:εf, tn、εf, tn-1分别为tn及tn-1时刻FRP的轴向应变。
| $ \Delta u{'_{{\rm{f}}n}} = {\varepsilon _{{\rm{f}},{t_n}}} - {\varepsilon _{{\rm{f}},{t_{n - 1}}}} = \frac{{\Delta {N_{{\rm{c}}n}}}}{{{E_{{\rm{c}},{t_n}}}{A_{\rm{c}}}}} + \frac{{{N_{{\rm{c}},{t_{n - 1}}}}}}{{{E_{{\rm{c}},{t_{n - 1}}}}{A_{\rm{c}}}}}\chi \left( {{t_{n - 1}},{t_n}} \right) \cdot \varphi \left( {{t_{n - 1}},{t_n}} \right) - {\varepsilon _{{\rm{sh}}}}, $ | (20) |
式中:εc, tn、εc, tn-1分别为tn及tn-1时刻混凝土部分的轴向应变。
将式(17)、(19)和(20)代入式(18)并联立式(9)可得关于ΔNcn的微分控制方程:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\Delta N'{'_{{\rm{c}}n}} - {{\bar \alpha }^2}\Delta {N_{{\rm{c}}n}} = \bar \beta \Delta {M_n} - \bar \gamma \Delta {F_n} - {K_{{t_{n - 1}}}}{\varepsilon _{{\rm{sh}}}} + \\ {K_{{t_{n - 1}}}}\frac{{{N_{{\rm{c}},{t_{n - 1}}}}}}{{{E_{{\rm{c}},{t_{n - 1}}}}{A_{\rm{c}}}}}\chi \left( {{t_{n - 1}},{t_n}} \right) \cdot \varphi \left( {{t_{n - 1}},{t_n}} \right) + \bar \beta \Delta {M_{{\rm{c}},{t_{n - 1}}}}\frac{{\chi \left( {{t_{n - 1}},{t_n}} \right) \cdot \varphi \left( {{t_{n - 1}},{t_n}} \right)}}{{1 + \chi \left( {{t_{n - 1}},{t_n}} \right) \cdot \varphi \left( {{t_{n - 1}},{t_n}} \right)}}, \end{array} $ | (21) |
式中:α2=Ktn-1
文献[15]中认为胶层的徐变性能与混凝土类似,故胶层的剪切刚度为
| $ {K_{{t_{n - 1}}}} = \frac{{{b_{\rm{a}}}{G_{\rm{a}}}}}{{{t_{\rm{a}}}\left( {1 + {\chi _{\rm{a}}}{\varphi _{\rm{a}}}} \right)}}, $ | (22) |
式中:ba胶层的宽度;Ga胶层的剪切模量;ta胶层的厚度;χa为tn-1时刻胶层的老化系数,φa为tn-1时刻胶层的徐变系数。胶层的徐变系数和老化系数可参照混凝土相应系数的计算方法计算。
在均布荷载q作用下,加固梁跨中截面,作用在混凝土部分的轴向力增量最大值为
| $ \begin{array}{l} \Delta {N_{{\rm{cn,max}}}} = \lambda \frac{{q{L^2}}}{8}\frac{{{E_{{\rm{c}},{t_n}}}{I_c}}}{{E{I_{{t_n}}}}} + \frac{{q\lambda }}{{{{\bar \alpha }^2}d}}\left( {1 - \frac{{{E_{{\rm{c}},{t_n}}}{I_c}}}{{E{I_{{t_n}}}}}} \right)\left[ {1 - \frac{1}{{\cos \left( {\frac{{\bar \alpha L}}{2}} \right)}}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{K_{{t_{n - 1}}}}{\varepsilon _{{\rm{sh}}}}}}{{{{\bar \alpha }^2}}}\left[ {1 - \frac{1}{{\cos \left( {\frac{{\bar \alpha L}}{2}} \right)}}} \right] - \lambda \frac{{{M_{{\rm{c}}{t_{n - 1,{\rm{msx}}}}}}}}{d}, \end{array} $ | (23) |
式中:EItn=Ec, tnIc+
| $ \begin{array}{l} \Delta {N_{{\rm{cn,max}}}} = \lambda \frac{{q{L^2}}}{8}\frac{{{E_{{\rm{c}},{t_n}}}{I_c}}}{{E{I_{{t_n}}}}} + \frac{{q\lambda }}{{{{\bar \alpha }^2}d}}\left( {1 - \frac{{{E_{{\rm{c}},{t_n}}}{I_c}}}{{E{I_{{t_n}}}}}} \right)\left[ {1 - \frac{1}{{\cos \left( {\frac{{\bar \alpha L}}{2}} \right)}}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{K_{{t_{n - 1}}}}{\varepsilon _{{\rm{sh}}}}}}{{{{\bar \alpha }^2}}}\left[ {1 - \frac{1}{{\cos \left( {\frac{{\bar \alpha L}}{2}} \right)}}} \right] - \lambda \frac{{{M_{{\rm{c}}{t_{n - 1,{\rm{msx}}}}}}}}{d}, \end{array} $ |
对于没有发生端部锚固破坏的预应力CFRP布加固的钢筋混凝土梁,界面滑移较小,可以忽略不计。因此,认为胶层的剪切刚度很大,即Ktn-1→∞,公式(23)可以改写为
| $ \Delta {N_{{\rm{cn,max}}}} = \lambda \frac{{q{L^2}}}{8}\frac{{{E_{{\rm{c}},{t_n}}}{I_c}}}{{E{I_{{t_n}}}}} + \frac{{{\varepsilon _{{\rm{sh}}}}}}{{\frac{{E{A_{{t_n}}}}}{{E{A_0}}} + \frac{{{d^2}}}{{{E_{{\rm{c}},{t_n}}}{I_c}}}}} - \lambda \frac{{{M_{{\rm{c}}{t_{n - 1,{\rm{msx}}}}}}}}{d}, $ | (24) |
式中:EAtn=Ec, tnAc+EfAf。
假设ΔMn=0,ΔFn=0,则跨中截面混凝土部分在tn时刻的最大弯矩为
| $ {M_{{\rm{c}}{t_{n{\rm{,max}}}}}} = {M_{{\rm{c}}{t_{n - 1,{\rm{msx}}}}}} + \Delta {N_{{\rm{c}}n{\rm{ - 1,max}}}}d, $ | (25) |
在划分的每一个时间段内,重复公式(24)和(25)可得
| $ \Delta {N_{\rm{f}}} = - \Delta {N_{\rm{c}}} = \sum\limits_{i = 1}^n {\Delta {N_{{\rm{c}}n{\rm{,max}}}}} , $ | (26) |
则由混凝土收缩徐变和胶层徐变引起的预应力损失为
| $ {\sigma _{{\rm{CR}}}} = \frac{{\Delta {N_{\rm{f}}}}}{{{A_{\rm{f}}}}}, $ | (27) |
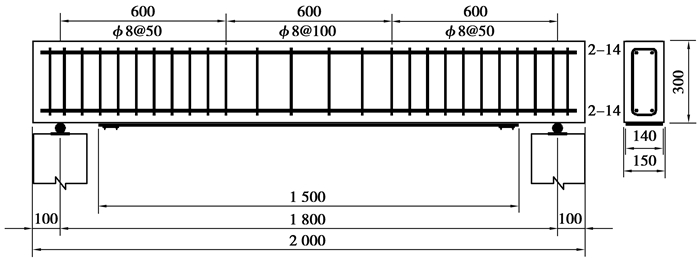
文献[2]进行了4根预应力CFRP布加固的钢筋混凝土梁预应力损失试验如图 2所示。试验梁为矩形截面钢筋混凝土梁,截面宽150 mm,高300 mm。受拉和受压区分别配置2根直径为14 mm的HRB335级钢筋,箍筋为直径8 mm的R235级钢筋,间距50 mm。试验梁长2 000 mm,净跨径为1 800 mm。使用的CFRP布宽度为140 mm,厚度为0.167 mm。粘贴的层数分别为1层、2层,施加的初始预应力大小为0.28~0.40倍CFRP布的极限抗拉强度。试验梁BPC-30-1、BPC-40-1及BPC-30-2预应力CFRP布在胶层胶体养护3 d后放张,而试验梁BPC-30-2a为张拉到设计初始预应力后即刻放张。
表 1给出了瞬时预应力损失、短期和长期预应力损失预测值与试验值的比较,表 2为材料力学性能。可以看出,对于文献[2]中的试验梁,瞬时预应力损失预测值与试验值最大差值仅为6.3 MPa,长期损失预测值与试验值最大差值为39.6 MPa,总损失预测值与试验值最大差值为45.9 MPa,占总损失实测值的20.3%。虽然出现一定的误差,但是在可接受的范围内,因此文中建立的模型可以用于预应力长期损失的预测。
| 表 1 预应力损失试验值与预测值的比较 Table 1 Comparisons between the predicted values and experimental ones of prestress losses |
| 表 2 材料力学性能表 Table 2 Mechanical propertiesof the material |
建立了考虑混凝土收缩徐变、胶层徐变及界面滑移的预应力CFPR布加固钢筋混凝土梁预应力长期损失微分增量方法。该方法将时间划分为有限个时间段,每个时间段内采用有效模量法,在给定的边界条件及荷载形式下,得到了预应力长期损失的闭合解。为验证建立的微分增量法的有效性,对相关文献中的试验梁进行了计算分析。计算结果表明,长期预应力损失计算值与试验值有差异,但是在可接受的范围之内,建立的微分增量模型可以用于预应力长期损失的预测。
| [1] |
王文炜. FRP加固混凝土结构技术及应用[M]. 北京: 中国建筑工业出版社, 2007.
WANG Wenwei. Technology and application of FRP reinforced concrete structure[M]. Beijing: China building industry press, 2007. (in Chinese) |
| [2] | Wang W W, Dai J G, Harries K A, et al. Prestress Losses and Flexural Behavior of Reinforced Concrete Beams Strengthened with Posttensioned CFRP Sheets[J]. American Society of Civil Engineers, 2014, 16(2): 207–216. |
| [3] | Wang W W, Dai J G, Harries K A. Intermediate crack-induced debonding in RC beams externally strengthened with prestressed FRP laminates[J]. Journal of Reinforced Plastics & Composites, 2013, 32(23): 1842–1857. |
| [4] |
王文炜, 戴建国, 张磊.
后张预应力碳纤维布加固钢筋混凝土梁预应力损失试验及计算方法研究[J]. 土木工程学报, 2012, 45(11): 88–94.
WANG Wenwei, DAI Jianguo, ZHANG Lei. Experimental study and anaytical modeling of prestress losses of reinforced concrete beams strengthened with post-tensioned CFRP sheets[J]. China Civil Engineering Journal, 2012, 45(11): 88–94. (in Chinese) |
| [5] | Kim Y J, Wight R G, Green M F. Flexural Strengthening of RC Beams with Prestressed CFRP Sheets:Development of Nonmetallic Anchor Systems[J]. Journal of Composites for Construction, 2008, 12(1): 35–43. DOI:10.1061/(ASCE)1090-0268(2008)12:1(35) |
| [6] | Xue W, Tan Y, Zeng L. Flexural response predictions of reinforced concrete beams strengthened with prestressed CFRP plates[J]. Composite Structures, 2010, 92(3): 612–622. DOI:10.1016/j.compstruct.2009.09.036 |
| [7] | Elhacha R, Wight R G, Green M F. Prestressed Carbon Fiber-Reinforced Polymer Sheets for Strengthening Concrete Beams at Room and Low Temperatures[J]. Journal of Composites for Construction, 2014, 8(1): 3–13. |
| [8] |
薛伟辰, 曾磊, 谭园.
预应力CFRP板加固混凝土梁设计理论研究[J]. 建筑结构学报, 2008, 29(4): 127–133.
XUE Weichen, ZENG Lei, TAN Yuan. Prestressed CFRP plate reinforced concrete beam design theory research[J]. Journal of Building Structures, 2008, 29(4): 127–133. (in Chinese) |
| [9] | Pellegrino C, Modena C. Flexural Strengthening of Real-Scale RC and PRC Beams with End-Anchored Pretensioned FRP Laminates[J]. Aci Structural Journal, 2009, 106(3): 319–328. |
| [10] | Quantrill R J, Hollaway L C. The flexural rehabilitation of reinforced concrete beams by the use of prestressed advanced composite plates[J]. Composites Science\s & \stechnology, 1998, 58(8): 1259–1275. |
| [11] | Woo S K, Nam J W, Kim J H J, et al. Suggestion of flexural capacity evaluation and prediction of prestressed CFRP strengthened design[J]. Engineering Structures, 2008, 30(12): 3751–3763. DOI:10.1016/j.engstruct.2008.06.013 |
| [12] | Meier. U.Strengthening of structures using carbon fibre/epoxy composites[J]. Construction and Building Materials, 1995, 9(6): 341–351. DOI:10.1016/0950-0618(95)00071-2 |
| [13] | El-Hacha R, Wight R G, Green M F. Prestressed fibre‐reinforced polymer laminates for strengthening structures[J]. Progress in Structural Engineering and Materials, 2001, 3(2): 111–121. DOI:10.1002/(ISSN)1528-2716 |
| [14] | El-Hacha R, Wight R G, Green M F. Innovative system for prestressing fiber-reinforced polymer sheets[J]. Aci Structural Journal, 2003, 100(3): 305–313. |
| [15] | Diab H, Wu Z, Iwashita K. Short and long-term bond performance of prestressed FRP sheet anchorages[J]. Engineering Structures, 2009, 31(5): 1241–1249. DOI:10.1016/j.engstruct.2009.01.021 |
| [16] | Kim Y J, Green M F, Wight R G. Bond and Short-term Prestress Losses of Prestressed Composites for Strengthening PC Beams with Integrated Anchorage[J]. Journal of Reinforced Plastics and Composites, 2010, 29(9): 1277–1294. DOI:10.1177/0731684409102751 |
| [17] |
项海帆. 高等桥梁结构理论[M]. 北京: 人民交通出版社, 2001.
XIANG Haifan. Advanced bridge structure theory[M]. Beijing: People's Traffic Press, 2001. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38