三维传感技术在物体形貌测量、物质表面特性检测以及医学等领域有广泛的应用前景,在诸多三维传感技术中,基于位相法的光学三维传感技术由于具有非接触、精度高、速度快等特点,是三维形貌测量的主要方法[1-5]。光学相位三维测量方法首先向被测物体投射影栅图案,通过比较影栅图案被调制前后的相位差分布重建物体表面三维信息。由于该方法得到的是(-π, π)之间的主值相位,需要采用适当的去包裹方法将其展开为连续相位。但是,实际的影栅条纹或干涉条纹面临断层、阴影区、各种系统噪声等干扰,传统解包裹方法会出现误差传播,无法得到正确的展开相位值,因此相位解包裹是光学相位三维测量方法的关键问题。为此,提出了各种相位解包裹方法[6-17],其中德国学者Huntley等提出的时间相位解包裹算法[14-15]沿时间轴对每个像素进行独立展开,从原理上避免了空间相位展开出现的拉线现象。文中在田劲东等[18]提出的广义时间相位解包裹方法的基础上,设计了1个三维形貌测量系统,并对其进行了实测实验。结果表明,该系统可以实现对物体形貌的快速、高效测量。
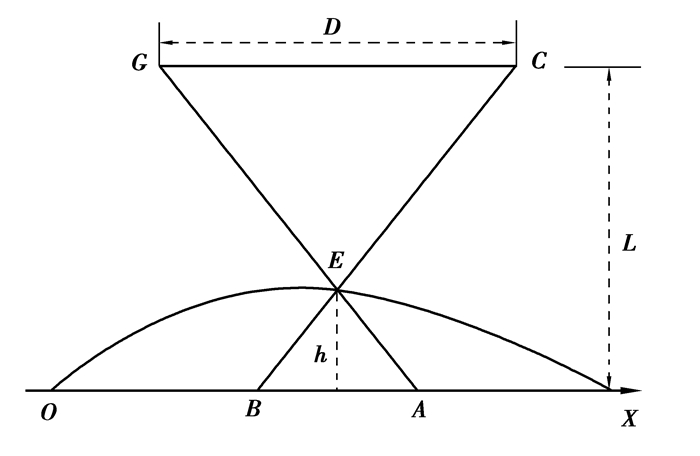
1 系统原理系统的光路原理图如图 1所示,G为投影仪, C为摄像机,CG的连线平行于参考平面OX,待测物体放置于参考平面上,从投影仪发出的余弦光栅投射于参考平面。投影仪G与摄像机C光心之间的距离为D,摄像机C到参考平面的距离为L。
|
图 1 系统光路原理 Figure 1 Principle of optical system |
令投射在平面OX上的光场分布为
| $ {I_1}\left( {x,y} \right) = a\left( {x,y} \right) + b\left( {x,y} \right)\cos \left[ {\varphi \left( {x,y} \right)} \right]。 $ | (1) |
放置物体后,由于物体表面形貌的调制,摄像机采集到的光场分布变为
| $ {I_2}\left( {x,y} \right) = a\left( {x,y} \right) + b\left( {x,y} \right)\cos \left[ {\varphi \left( {x,y} \right) + \Delta \varphi \left( {x,y} \right)} \right], $ | (2) |
式中, Δφ为放置物体前后的相位变化量。
若放置物体前光束投射于参考平面上A点,则放置物体后将投射到物体表面上的E点,其相位与参考平面上B点的相位相同,A、B两点之间的相位差即为Δφ。令影栅的频率为f0,A、B两点之间的距离为|AB|则
| $ \Delta \varphi = 2\pi {f_0}\left| {AB} \right|。 $ | (3) |
由于CG平行于参考平面,设物体在E点的高度为h,则由图 1的几何关系可得
| $ \left| {AB} \right| = \frac{h}{{L - h}}D, $ | (4) |
所以,
| $ \Delta \varphi = 2\pi {f_0}\frac{{hD}}{{L - h}}, $ | (5) |
| $ h = \frac{{L\Delta \varphi }}{{2\pi {f_0}D + \Delta \varphi }}。 $ | (6) |
因此,只要知道放置物体前后的相位差分布Δφ,即可测得物体表面形貌。
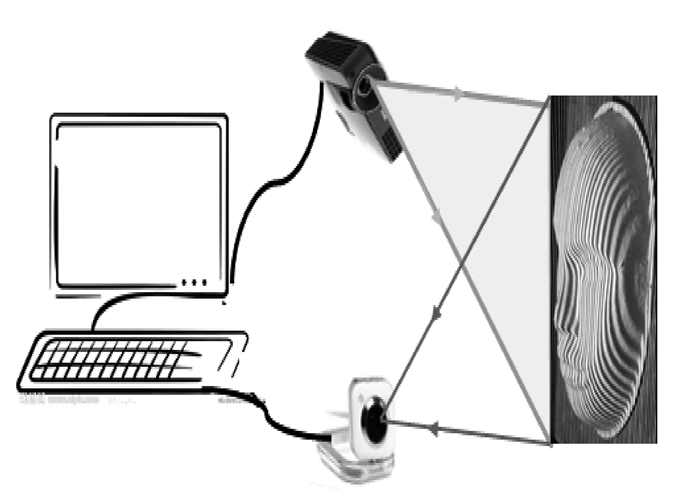
2 系统实现整个系统主要由载物台、投影仪、摄像机、计算机及软件组成,如图 2所示。计算机产生一定频率和相移量的余弦影栅图案条纹,经投影仪投射到载物台所在平面,摄像机对载物台上的影栅图案成像,并送入计算机,经系统处理分析后得到物体的三维形貌。
|
图 2 系统组成 Figure 2 System of shape measurement |
系统主要由影栅投影模块、图像采集模块、相位求解模块和三维重建模块等4个功能模块组成。投影模块的任务是按照一定空间的频率和相移量产生余弦影栅条纹并将其投射到放置在参考平面的物体表面,图像采集模块对调制后的影栅图进行采集,相位求解模块对采集到的图像进行相位分析以得到调制前后的相位差图,三维重建模块根据相位差图以及成像时的外部参数重建物体的三维表面形貌。在所有这些功能模块中,相位求解模块是能否准确重建物体形貌的关键,它包括获取主值相位图和相位解包裹等2个依序进行的环节。
2.1 四步相移法获取主值相位图影栅空间为f0时,计算机产生4幅相移量依次为0、π/4、π/2和3π/4、270°的余弦光栅。
| $ {I_1} = a\left( x \right) + b\left( x \right)\cos \left( {2\pi {f_0}x} \right), $ | (7) |
| $ {I_2} = a\left( x \right) + b\left( x \right)\cos \left( {2\pi {f_0}x + \frac{\pi }{4}} \right), $ | (8) |
| $ {I_3} = a\left( x \right) + b\left( x \right)\cos (2\pi {f_0}x + \frac{\pi }{2}), $ | (9) |
| $ {I_4} = a\left( x \right) + b\left( x \right)\cos (2\pi {f_0}x + \frac{{3\pi }}{4}), $ | (10) |
则空间某点(x, y)的相位为
| $ {\mathit{\Phi} _w} = 2\pi {f_0}x = {\tan ^{ - 1}}\frac{{{I_4} - {I_2}}}{{{I_1} - {I_3}}}。 $ | (11) |
利用上式得到的相位图的取值范围被包裹在(-π, π)之间,称为主值相位图。主值相位图是不连续的,需要通过解包裹方法将其变为连续分布的相位图,以反映真实的相位变化。
2.2 广义时间相位解包裹方法时间相位解包裹的基本思想是向参考平面投影多个空间频率的影栅图案,首先利用四步相移法计算出不同空间频率下的主值相位,然后在时间轴上按照频率由低到高依序进行解包裹处理,最后得到系统的解包裹相位图。
令投影到参考平面的影栅图案长度为W,定义影栅的空间频率为W长度内出现的影栅条纹数目,则频率为f时,沿垂直于栅线的x方向的相位分布为
| $ \varphi = \frac{{2\pi }}{w}fx,\left( {x = 0,1, \cdots ,W} \right)。 $ | (12) |
若f=1,则沿x方向的相位分布范围为(-π, +π),因此其解包裹相位和主值相位是一致的,即
| $ {\mathit{\Phi} _{\rm{u}}}\left( 1 \right) = {\Phi _w}\left( 1 \right), $ | (13) |
其中下标U表示解包裹相位。
若f2=kf1(k > 1),则相位解包裹可表示为
| $ {\mathit{\Phi} _{\rm{u}}}\left( {{f_2}} \right) = {\mathit{\Phi} _{\rm{w}}}\left( {{f_2}} \right) - 2\pi \times NINT\left( {\frac{{{\mathit{\Phi} _{\rm{w}}}\left( {{f_2}} \right) - k{\mathit{\Phi} _{\rm{u}}}\left( {{f_1}} \right)}}{{2\pi }}} \right)。 $ | (14) |
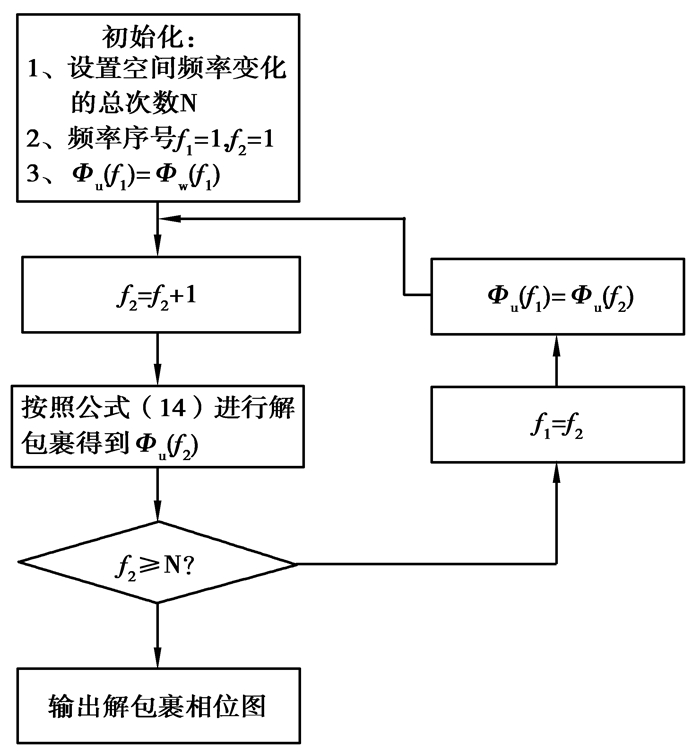
时间相位解包裹的具体流程如图 3所示。
|
图 3 时间相位解包裹流程 Figure 3 Chart of GPTU |
系统装置由LG HX300G投影仪、大恒HV1351UM型号CCD摄像机、载物台和相关软件系统组成,摄像机到投影仪光心间距D=350 mm,摄像机到参考平面的距离为750 mm,最大频率时的光栅常数T=5.5 mm,软件系统使用matlab2012b编写,使用levono thinkPad E430笔记本电脑,内存8 G,64位windows 7操作系统作为软件平台。英国学者David提出的机遇可靠度排序的解包裹算法是目前效果比较好的空间相位解包裹方法[11]。
将图 4所示的人脸面具垂直安置在载物平台上,图 5是某一空间频率的余弦影栅投影到面具上获取的被物体表面形貌调制后的影栅图。图 6是得到的包裹相位图,由于相位值被包裹在(-π,+π)之间呈不连续分布,因此无法反映真实相位分布。

|
图 4 被测物体 Figure 4 Object |

|
图 5 调制后的影栅图 Figure 5 The modulated fringe |

|
图 6 包裹相位图 Figure 6 Wrapped phase map |
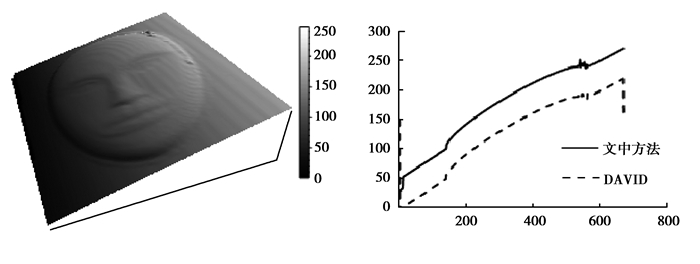
图 7是利用时间相位解包裹方法得到的解包裹相位图,为了更清楚地观察,采用立体投影方式显示,可见解包裹后能够真实地反映相位随物体表面形貌的分布。坐标图中实线部分是相位图中第150行的相位分布,虚线部分是david方法得到的结果。可以看出,2种方法都可以得到正确反映物体形貌的连续相位分布。区别在于,2种方法的结果相差一个常数,由于David方法无法有效处理边界附近的像素,因此其曲线两端出现了跳变。另外,在物体与参考平面的右交界处有一定的相位误差。
|
图 7 解包裹相位图 Figure 7 Unwrapped phase map |
图 8(a)和(b)是分别使用文中方法和David方法测得的物体形貌图。从图中可以清晰地观察到物体的眼眶、眼睛、鼻子和嘴巴等主要部位,物体的轮廓特征明显。也可以看到,在额头的右上方出现了明显的误差,这主要是由于光场是从右向左照射,该处由于高度剧烈变化导致局部欠采样所致,下一步拟采用旋转成像结合图像拼接的方法加以消除。图 8(c)是第150行的高度变化曲线对比,为了便于比较,将2条曲线作了一定的平移。可以看出,2条曲线的形状基本相同。物体鼻尖到参考平面的实际高度是68 mm,实测的高度是67.66 mm。上述对比实验说明,文中方法和David方法具有同样高的精度。

|
图 8 效果图对比 Figure 8 Results |
多次实测结果表明,使用David方法需要的平均运行时间在360~420 s,而采用文中方法平均需要4~6 s时间。因此,文中方法的运行效率明显优于David方法。
4 结束语设计实现了一种基于时间相位解包裹方法的三维形貌测量系统,重点介绍了基于时间相位解包裹方法的相位求解模块。对人脸面具的实测实验表明,该系统可以快速、准确地完成物体形貌测量。对于由于局部欠采样引起的实验误差,拟在以后的工作中通过旋转成像加图像拼接的方法加以改进。
| [1] | Zhong M, Chen W, Su X. Comparison of fringe pattern phase retrieval using 2D wavelet trasform and S-Transform[C]//Optical Fibre Technology, 2014 OptoElectronics and Communication Conference and Australian Conference on. IEEE, 2014:850-852. |
| [2] | Casavola C, Pappalettera G, Pappalettere C. Design of a fiber optics fringe projector for 3D reconstruction of dental elements[C]//Photonics Conference, 2014 Third Mediterranean. IEEE, 2014:1-3. |
| [3] |
王华荣, 李彬, 王志峰, 等.
基于条纹反射术的槽式抛物面单元镜面形测量[J]. 光学学报, 2013, 33(01): 130–133.
WANG Huarong, LI Bin, WANG Zhifeng, et al. Surface Measurement of Parabolic trough unit mirror based on fringe refelection[J]. Acta Optic Sinica, 2013, 33(01): 130–133. (in Chinese) |
| [4] | Zhong K, Li Z, Shi Y, et al. Fast phase measurement profilometry for arbitrary shape objects without phase unwrapping[J]. Optics and Lasers in Engineering, 2013, 51(11): 1213–1222. DOI:10.1016/j.optlaseng.2013.04.016 |
| [5] |
武子靖, 董萼良, 陈耀忠, 等.
基于栅线投影法对牙冠三维形貌的研究[J]. 东南大学学报(医学版), 2010(05): 494–497.
WU Zijing, DONG Eliang, CHEN Yaozhong, et al. Study on three-dimensional (3-D) profile measure of the dental crowns based on grating projection[J]. Journal of Southeast University (Medical Edition), 2010(05): 494–497. (in Chinese) |
| [6] |
王华英, 刘佐强, 廖薇, 等.
基于最小范数的四种相位解包裹算法比较[J]. 中国激光, 2014(2): 130–135.
WANG Huaying, LIU Zuoqiang, LIAO Wei, et al. Comparison of four phases unwrapping algorithm based on method of minimum norm[J]. Chinese Journal of Lasers, 2014(2): 130–135. (in Chinese) |
| [7] |
郭媛, 陈小天.
基于最小二乘相位解包裹改进算法的研究[J]. 中国激光, 2014(05): 195–200.
GUO Yuan, CHEN Xiaotian. Study of improved phase unwrapping algorithm based on least squares[J]. Chinese Journal of Lasers, 2014(05): 195–200. (in Chinese) |
| [8] |
廖薇, 刘佐强, 王华英, 等.
三种基于路径跟踪的位相解包裹算法比较[J]. 激光杂志, 2014(06): 32–34.
LIAO Wei, LIU Zuoqiang, WANG Huaying, et al. Comparison of the three phase unwrapping algorithm based on the algorithm of Path tracking[J]. Lasernal, 2014(06): 32–34. (in Chinese) |
| [9] | Liu G, Wang R, Deng Y, et al. A New Quality Map for 2-D Phase Unwrapping Based on Gray Level Co-Occurrence Matrix[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(2): 444–448. DOI:10.1109/LGRS.2013.2264857 |
| [10] | Zhong H, Tang J, Zhang S, et al. A Quality-Guided and Local Minimum Discontinuity Based Phase Unwrapping Algorithm for InSAR/InSAS Interferograms[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(1): 215–219. DOI:10.1109/LGRS.2013.2252880 |
| [11] | Herráez M A, Burton D R, Lalor M J, et al. Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path[J]. Applied Optics, 2002, 41(35): 7437–7444. DOI:10.1364/AO.41.007437 |
| [12] | Huntley J M, Ruiz P D. Full field measurements and identification in solid mechanics depth-resolved phase imaging[J]. Procedia IUTAM, 2012, 4(0): 82–91. |
| [13] | Davila A, Ruiz P D, Kaufmann G H, et al. Measurement of sub-surface delaminations in carbon fibre composites using high-speed phase-shifted speckle interferometry and temporal phase unwrapping[J]. Optics and Lasers in Engineering, 2003, 40(5/6): 447–458. |
| [14] | Huntley J M, Coggrave C R. Progress in phase unwrapping[C]//International Conference on Applied Optical Metrology. International Society for Optics and Photonics, 1998. |
| [15] | Saldner H O, Huntley J M. Shape measurement of discontinuous objects using projected fringes and temporal phase unwrapping[C]//3-D Digital Imaging and Modeling, 1997. Proceedings., International Conference on Recent Advances in. IEEE, 1997:44. |
| [16] |
陈小宁, 刘先勇, 姚一永, 等.
应用于三维测量的彩色编码相位求解技术[J]. 微计算机信息, 2010(28): 205–207.
CHEN Xiaoning, LIU Xianyong, YAO Yiyong, et al. A new unwrapping method combined with phase shift processing and color-coded light[J]. Micro Computer Information, 2010(28): 205–207. (in Chinese) |
| [17] | Chen F, Zhuang W. A Phase Unwrapping Algorithm for Discontinuous Object Measurement[C]//Photonics and Optoelectronic (SOPO), 2010 Symposium on. IEEE, 2010:1 -4. |
| [18] | Tian J D, Peng X, Zhao X B. A generalized temporal phase unwrapping algorithm for three-dimensional profilometry[J]. Optics and Lasers in Engineering, 2008, 46(4): 336–342. DOI:10.1016/j.optlaseng.2007.11.002 |
 2015, Vol. 38
2015, Vol. 38

