由于工程爆破具有快速、经济和安全等优点,所以随着国民经济的高速发展,工程爆破技术在矿山、水利水电、铁路、交通、建筑等各个领域得到了广泛的应用,并在其中起着举足轻重的作用。炸药爆炸使岩体类结构体发生破裂、破碎及抛掷,这是爆炸应力波和爆生气体膨胀共同作用的结果。爆破作用是一个瞬间完成的高温高压过程,岩石类材料本身具有非均匀性、非弹性和各向异性,这导致其在爆炸载荷作用下是一个复杂的物理、力学过程[1-2]。空气中和水下爆炸时的物理机制和介质运动已经研究的很全面和很详尽,相比之下岩石中地下爆炸的物理机制、介质的运动和破坏的研究还很不透彻[3-6]。
目前,对于岩石爆破的物理机制,国内外众多科研工作者从力学模型[7]、断裂损伤[7-12]、能量原理[2, 13-14]、数值计算[15]和实验[16-17]等方面进行了大量研究,但其成果与工程实际应用的需要相距甚远[18-19]。爆破应力波在工作介质中的传播规律是解决该问题的基础。根据应力波理论,应力波在介质中传播发生的衰减可分为几何衰减和物理衰减:几何衰减是因能量分布空间的增大而衰减;物理衰减是波在传播过程中与介质作用而导致其携带的能量转变为其它形式的能量,如形成新岩块表面的表面能,由耗散生成的热能等。对于球形药包爆破应力波理论,经过前苏联科学家的努力,已获得了广为大家接受的应力波方程。柱状药包与球形药包的爆破应力波在传播过程中,在相同距离的条件下,其分布空间是不同的,故衰减也不同[14]。因此,用球形药包理论来处理柱状药包问题在本质上是不合适的。这里采用系统的实验手段对柱状药包在混凝土试件中爆破应力波进行试验测试与分析。
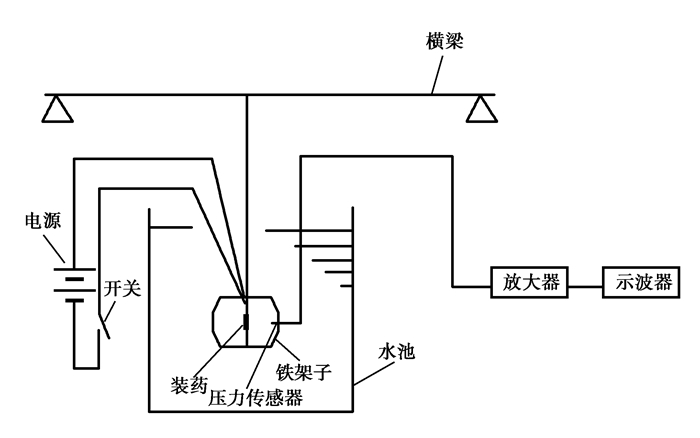
1 柱状药包参数的水下爆炸测试由于试验用的水泥砂浆试块体积不大,所需药量很小,炮孔直径也很小,只有几个毫米,所以使用工业炸药是不合适的。本试验采用的是二硝基重氮酚(DDNP)作为爆源,装药密度为ρ0=0.82 g/cm3,爆速为v=3 991 m/s。药包直径为3.5 mm。试验所用爆炸水池φ5.5 m、高3.62 m。为避免炸药爆炸后来自水面和水池底部冲击反射的干扰,将装药在水池中心三分之二深度处爆炸,以消除边界效应。水下爆炸测试系统如图 1所示。
|
图 1 实验装置示意图 Figure 1 Schematic diagram of experimental device |
根据P.库尔的研究[20],炸药水下爆炸冲击波压力计算公式
| Pm=k(W13R)α, | (1) |
式中: Pm为冲击波压力,MPa;W为标定药包的重量,kg;R为传感器至药包中心的距离,这里其为0.237 m;k、α为与实验有关系数和指数。
试验测试数据如表 1所示,采用最小二乘法对实验数据进行曲线拟合,得到k=41.45 MPa, α=1.235。
| 表 1 柱状药包水下爆炸压力试验数据 Table 1 Data of pressure of cylindrical charge blasting under water |
药包爆炸时在爆破工作面上产生的压力可达5~10万个大气压,爆炸载荷首先在炮孔附近区域形成冲击波。随着冲击波的传播,爆炸能量向四周扩散,岩石介质中产生短时间的高压和高温,其使得岩石中形成压碎圈。压碎圈的形成将消耗冲击波中很大一部分能量,导致冲击波衰减很快。因此,炸药爆破岩石的作用是先形成爆炸冲击波,而后其衰减成应力波。
关于爆炸应力波的研究较为成熟的是集中装药的球形药包,而在工程实践中,常采用等效球形药包理论的方法来计算柱状药包参数,即用集中药包的理论和公式计算柱状药包应力场参数,而后将其药量均匀拉长分布或乘以一经验系数来修正。关于柱状药包爆炸产生的冲击波在介质中的衰减规律一般用式(2)表示[21]。
| σr=σmˉrα, | (2) |
式中:
| 表 2 不同岩石爆破应力波衰减系数 Table 2 The attenuation parameters of explosive stress waves of different rocks |
当冲击波衰减为应力波后,若此时假定岩石为理想弹性介质,就可以由应力波理论推导出其传播方程。应力波在传播过程中,波阵面应满足质量守恒和动量守恒两定律,即运动学相容条件和动力学相容条件。柱状药包在弹性介质中爆炸激起的应力波应为柱面波或近似柱面波。
采用Lagrange柱坐标r, θ, z,其中只有径向位移ur(r, t)非零,且其只是r, t的函数。由动量守恒条件可得柱面波的径向运动方程:
| ∂σr∂r+σr−σθr=ρ0∂v∂t。 | (3) |
根据广义虎克定律可得到应力的表达式:
| σr=(λ+2G)θ2Gurr,σθ=λθ+2Gurr,σz=λθ. | (4) |
所以柱面波的波前应力为:
| σr=√r0rσm. | (5) |
显然,柱状药包的爆炸应力波在不同区域传播时衰减系数差异较大。在近中区,药包爆炸在介质中产生的是冲击波,衰减规律如式(2)所示,其衰减系数大于在1~3之间;在远区,产生的是弹性应力波,衰减规律如式(5)所示,其衰减系数是0.5。
3 柱状药包在砂浆试块中的爆炸测试砂浆试块配比为:水泥:黄沙:水=1:2:0.5。通过在材料试验机和CTS-25型非金属超声波检测仪进行测试,得到混凝土的物理力学参数,如表 3所示。
| 表 3 水泥砂浆试块物理力学参数 Table 3 Cement mortar specimen mechanical parameters |
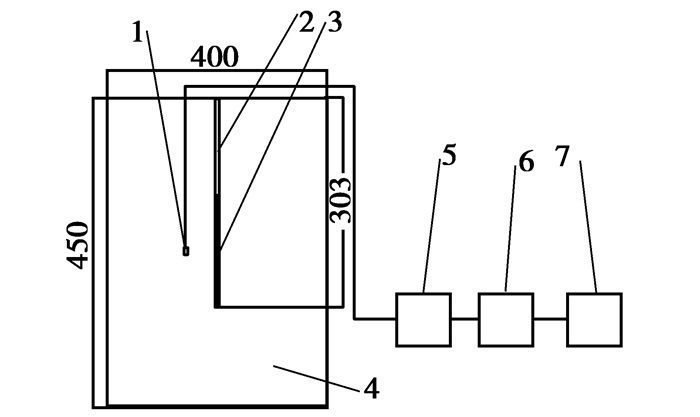
混凝土试件采用圆柱体,直径为400 mm, 高为450 mm。药包在水泥砂浆中爆破应变测试装置如图 2所示。预埋的应变砖所用的材料和配比与混凝土试件相同,以保证它们波阻抗相等。应变砖尺寸为180 mm×20 mm×10 mm,每块应变砖上布置4个测点,其到炮孔的距离分别为4,8,13,18 cm。
|
图 2 爆炸应变波测定装置示意图(单位:mm) Figure 2 Schematic diagram of blasting strain wave measuring device (Unit: mm) 1-应变砖;2-堵塞;3-柱状药包;4-水泥砂浆试块;5-SDY2107A型超动态应变仪;6-TST3406C动态测试分析仪;7-计算机 |
实验采用的是柱状药包,直径为3.5 mm,药量分别为:0.2,0.33,0.45,0.61,1.1 g。每一药量做2个为1组平行实验,根据前面的水下实验计算各种药量的药包其炮孔初始压力σm,如表 4所示。
| 表 4 混凝土试件炮孔中的初始爆炸应力 Table 4 The initial blasting stress of blast hole in concrete specimen |
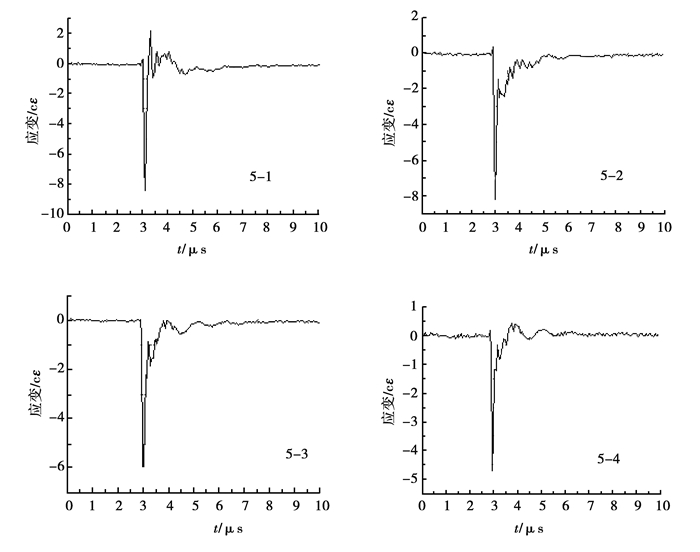
试验中没有发生应变砖被剥离的现象,这说明预埋的应变砖在试块中没有产生明显的界面效应,也证明这种预埋应变砖的方法是可行的。爆破的破碎块度较为均匀,以5号试块为例,其长径比是所有药包中最大的,其被爆破成完整的8块,如图 3所示。通过超动态应变仪测得的应变波形,如图 4所示。从所测波形图中得出,炸药在岩体中爆炸,在近区首先产生快速的压缩波,各测点应变急剧突跃,这时径向获得很大的负应变值。由于装药条件的不同,每组所测波形在细节上又各不相同。以5号试块为例,其应变波如图 4所示,由里向外依次为1、2、3、4号测点。5组试块测得的应变如表 5所示。

|
图 3 5#试块爆破效果图 Figure 3 The rendering of broken 5# specimen |
|
图 4 5#试块应变波图 Figure 4 Strain wave of 5# specimen |
| 表 5 混凝土试件中爆炸应变波测试结果 Table 5 Results of blasting strain wave in concrete specimen |
根据药包的水下测试得到炮孔的初始爆炸压力和混凝土的材料参数,对上表中数据进行拟合,得到爆炸应力波的衰减系数αi和平均衰减系数
试验结果与众多文献中给出的常见岩石中爆炸冲击波衰减系数相比偏小。试验所用的混凝土试块是水泥砂浆,没有粗骨料,浇注也是在实验室中完成的。试件的均匀性得到了保证,其致密性较好,微缺陷较少,所以其爆炸冲击波衰减系数比岩石的小,差异较大。
4 结论1)通过水下爆炸测试实验,得出了柱状药包的爆炸冲击波计算公式
2)通过预埋应变传感器方法,测得柱状药包在混凝土试件中的爆炸冲击波在混凝土介质中的衰减规律:
3)通过对应变波传播规律的实验数据的数值分析,得出了柱状药包在混凝土试件中衰减系数,其与爆炸冲击波在常见岩石中衰减系数有较大差异,对工程爆破实践有切实意义。
| [1] |
钱七虎.
岩石爆炸动力学的若干进展[J]. 岩石力学与工程学报, 2009, 28(10): 1945–1968.
QIAN Qihu. Some advances in rock blasting dynamics[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(10): 1945–1968. (in Chinese) |
| [2] | Sanchidrián J A, Segara P, Lopez L M. Energy components in rock blasting[J]. International Journal of Rock Mechanics and Mining Sciences, 2007(44): 130–147. |
| [3] |
范新, 王明洋, 谭可可.
爆炸荷载作用下深部块体变形运动规律研究[J]. 岩石力学与工程学报, 2007, 26(5): 1019–1025.
FAN Xin, WANG Mingyang, TAN Keke. Study on rule of block deformation and movement under explosion loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 1019–1025. (in Chinese) |
| [4] |
王明洋, 葛涛, 戚承志, 等.
爆炸荷载作用下岩石的变形与破坏研究(I)[J]. 防灾减灾工程学报, 2003, 23(2): 43–54.
WANG Mingyang, GE Tao, QI Chengzhi, et al. Study of deformation and failure of rock under explosion load (part I)[J]. Journal of Disaster Prevent and Mitigation Engineering, 2003, 23(2): 43–54. (in Chinese) |
| [5] |
王明洋, 王立云, 戚承志, 等.
爆炸荷载作用下岩石的变形与破坏研究(II)[J]. 防灾减灾工程学报, 2003, 23(3): 9–20.
WANG Mingyang, WANG Liyun, QI Chengzhi, et al. Study of deformation and failure of rock under explosion load (part II)[J]. Journal of Disaster Prevent and Mitigation Engineering, 2003, 23(3): 9–20. (in Chinese) |
| [6] |
王礼立.
爆炸与冲击荷载下结构和材料动态响应的新进展[J]. 爆炸与冲击, 2001, 21(2): 81–88.
WANG Lili. Progress in studies on dynamic response of structures and materials under explosive/impact loading[J]. Explosion and Shock Waves, 2001, 21(2): 81–88. (in Chinese) |
| [7] | Prasad U, Mohanty B, Nemes J A. Dynamic strength and fragmentation of selected rocks under impact loading [C]//4th North American Rock Mechanics Symposium, July 31-August 3, 2000, Seattle, Washiogton. Rotterdam: American Rock Mechanics Association, 2000: 577-82. |
| [8] |
李清.爆炸致裂的岩石动态力学行为与断裂控制试验研究[D].北京:中国矿业大学(北京), 2009. LI Qing. Experiment of fracture behaviors and control for crack propagation under blasting load[D]. Beijing: China University of Mining and Technology (Beijing), 2009. (in Chinese) http://www.cdmd.cnki.com.cn/Article/CDMD-11413-2009263111.htm |
| [9] |
张志呈.
定向断裂控制爆破机理综述[J]. 矿业研究与开发, 2000, 20(5): 40–42.
ZHANG Zhicheng. Summary of the mechanism of directional fracture controlled blasting[J]. Mining Research and Development, 2000, 20(5): 40–42. (in Chinese) |
| [10] | Hudaverdi T, Kulatilake P H S W, Kuzu C. Prediction of blast fragmentation using multivariate analysis procedures[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(12): 1318–33. DOI:10.1002/nag.v35.12 |
| [11] | Hamdi E, Bouden Romdhane N, du Mouza J, et al. Fragmentation energy in rock blasting[J]. Geotechnical and Geological Engineering, 2008, 26(2): 133–46. DOI:10.1007/s10706-007-9153-4 |
| [12] | Rinehart J S. Dynamic fracture strength of rocks[C]//Proceedings of the seventh symposium on rock mechanics. Pennsylvania: University Park, 1965. |
| [13] |
赵阳升, 冯增朝, 万志军.
岩体动力破坏的最小能量原理[J]. 岩石力学与工程学报, 2003, 22(11): 1781–1783.
ZHAO Yangsheng, FENG Zengchao, WAN Zhijun. Least energy principle of dynamical failure of rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(11): 1781–1783. (in Chinese) |
| [14] |
颜事龙.集中药包与条形药包爆破能量分布的研究[D].北京:铁道部科学研究院, 1994. YAN Shilong. Distribution of the explosive energy studied by concentrated charge and cylindrical charge[D]. Beijing: MOR Science Research Institute, 1994. (in Chinese) http://industry.wanfangdata.com.cn/yj/Detail/Thesis?id=Thesis_Y204988 |
| [15] |
王志亮, 郑明新.
基于TCK损伤本构的岩石爆破效应数值模拟[J]. 岩土力学, 2008, 29(1): 230–234.
WANG Zhiliang, ZHENG Mingxin. Numerical simulation of effect of rock blasting based on TCK damage constitutive model[J]. Rock and Soil Mechanics, 2008, 29(1): 230–234. (in Chinese) |
| [16] |
王伟, 李小春.
不耦合装药下爆炸应力波传播规律的试验研究[J]. 岩土力学, 2010, 31(6): 1723–1728.
WANG Wei, LI XiaoChun. Experimental study of propagation law of explosive stress wave under condition of decouple charge[J]. Rock and Soil Mechanics, 2010, 31(6): 1723–1728. (in Chinese) |
| [17] |
曾新华.岩石爆破损伤影响范围研究[D].天津:天津大学, 2003. ZEN Xinhua. Damage range studying of rock blasting[D]. Tianjin: Tianjin University, 2003.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10056-2004075489.htm |
| [18] |
黄文尧, 穆朝民, 宗琦, 等.
水胶药柱深孔预裂爆破弱化综采面硬岩断层分析[J]. 重庆大学学报, 2013, 36(7): 102–107.
HUANG Wenyao, MU Chaomin, ZONG Qi, et al. Analysis on weakening hard rock used by long-hole presplitting blasting fully mechanize coal face with water-gel explosive grain[J]. Journal of Chongqing University, 2013, 36(7): 102–107. (in Chinese) |
| [19] |
郭长宝, 张永双, 孙东生, 等.
挤压和剪切构造环境下深埋隧道岩爆对比研究[J]. 地质学报, 2011, 85(1): 66–77.
GUO Chang-bao, ZHANG Yong-shuang, SUN Dong-sheng, et al. Comparison study of rock bursts of deep buried tunnels in the shear and compression tectonic environments[J]. Acta Geologica Sinica, 2011, 85(1): 66–77. DOI:10.1111/acgs.2011.85.issue-1 (in Chinese) |
| [20] |
P库尔.水下爆炸[M].罗耀杰, 韩泽润, 官信, 等译.北京:国防工业出版社, 1960. Cole P. Underwater explosion[M]. LUO Yaojie, HAN Zerun, GUAN Xin, et al. trans. Beijing: National Defense Industry Press, 1960. (in Chinese) |
| [21] |
杨善元. 岩石爆破动力学基础[M]. 北京: 煤炭工业出版社, 1991: 74-78.
YANG Shanyuan. Dynamics base of rock blasting[M]. Beijing: China Coal Industry Publishing House, 1991: 74-78. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38


