在无线传感器网络中,节点的位置信息对传感器网络的监测活动至关重要。事件发生的位置和获取信息的节点位置是传感器节点监测消息中所包含的重要信息。因此, 设计适合无线传感器网络自身特点的定位系统和算法已成为无线传感器网络研究领域的热点。
传感器节点的定位就是根据少数已知位置的节点,按照某种定位机制确定自身的位置。根据定位过程中是否需要测量节点之间的距离或角度,现有的定位算法可分为两类:基于测距(range-based)的定位算法和无需测距的定位算法。基于测距的定位算法通常需要传感器网络中增加额外的硬件,如定时器、信号强度接收器、天线阵等来获取节点间传播时间、时间差、相关角度或者估计距离等,从而进一步对未知节点进行定位。常见的此类算法包括有RSSI (received signal strength indicator)[1-2]、TOA (time of arrival)[3]、TDOA (time difference on arrival)[4-5]、AOA (angel of arrival)[6-7]等。这类定位算法精度高,但是额外的硬件结构带来的高成本开销、高能量消耗与无线传感器网络对硬件的低要求和低功耗需求相悖。
而无需测距的定位算法不需要实际测量节点间的绝对距离和角度,依靠传感器节点和固定参考节点之间的连通性和网络拓扑结构来估算距离。参考节点已知自身位置,在进行周期性广播信息时,会广播他们的位置信息等。此类算法包括质心算法[8]、DV-Hop算法[9]、APIT算法[10]等。这类算法不需要额外的硬件,节点成本和功耗比较低,但是节点密度对定位精度影响很大,在节点分布不甚均匀时,精确度远不如基于测距的算法。由于此类算法与传感器网络低功耗等特点相适应,发展前景良好,近几年人们更多地关注于这类算法。但是,无需测距型算法的定位精度低于基于测距型算法,因此,很多研究致力于如何控制误差和提高算法的精确度。
现有的典型无需测距算法中,DV-Hop算法较易实现,国内外有很多研究对DV-Hop算法做出了改进[11-15]。文献[11]提出根据未知节点在一段时间内接收到锚节点信息的多少确定优先级,按照优先级高低决定锚节点定位顺序的先后。文献[14]在算法的第二阶段,运用数学工具修正了平均跳距的误差。文献[15]提出了2种新的算法并整合在一起,算法1用于节省能量消耗,当锚节点发生意外时,算法2用RSSI技术测量节点距离。就这些已改进的算法而言,文献[11]以增加锚节点为代价,文献[14]以增加计算量的能量消耗为代价,文献[15]以增加对无线传感器网络的依赖性为代价,来获取算法指标的提高。
这些改进和尝试重点集中于DV-Hop算法的前两步,例如当系统遭遇突发情况时使用RSSI技术来测量2点间距[15]和对平均距离的加权因子做出估计。在现有算法中,对于第三阶段的改进还不多,大多数研究采用数学理论优化节点位置坐标的计算[12]。但这些优化过程不是有一定的局限性,就是计算相对复杂,增加了节点的能量消耗。如文献[12]在算法的第三阶段,基于遗传算法,以网络的容错性和覆盖性为约束条件,以部署的成本为目标函数进行优化计算得到节点位置。但是这种改进要求预先计算节点位置并部署,在实际中,节点位置一般不能预先得到,而且基于遗传算法的计算过程相对复杂。为了尽量降低算法局限性,简化计算过程,提出了一种新的基于DV-Hop的改进算法,该算法不仅在算法第三阶段,构造了目标函数,利用非线性共轭梯度法得到未知节点的可能位置,而且综合了RSSI算法和无需测距算法的优点,即若存在一个未知节点,在一定范围内存在至少3个锚节点,那么在这个距离范围内,可以利用RSSI技术得到未知节点与每个锚节点的距离,并根据三边测量法得到未知节点的位置坐标,那么此后该未知节点便可以当做锚节点来使用。文中分析并改进了DV-Hop算法,致力于降低定位误差,提高定位精度,最后通过仿真验证改进算法可以有效提高定位精度。
1 系统模型 1.1 网络模型把传感器网络模拟为一个无向图,在这个图中,每个顶点v∈V代表一个传感器节点,V表示传感器节点集合。在本文中,假设每个传感器节点的通信半径都是相同的。顶点m和n构成的无序对(m, n)表示两个顶点间的一条边e=(m, n),意味着顶点m和n所代表的传感器节点都在对方的通信半径内。
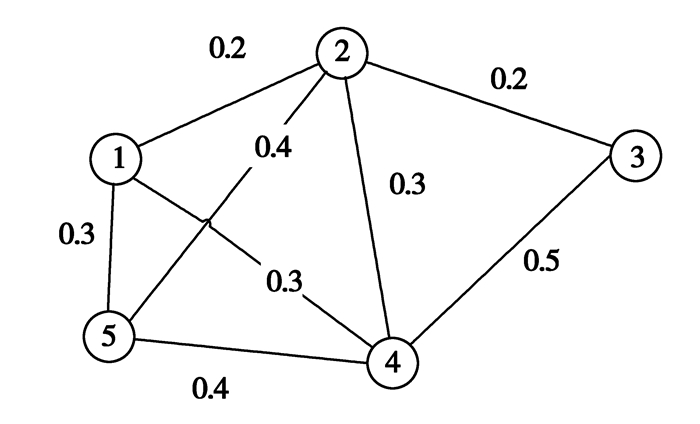
如图 1所示,此无向图中有5个顶点,8条边。其中,顶点1、2、4、5相互连接,顶点3仅与顶点2、4相连。
|
图 1 由5个顶点、8条边组成的网络拓扑图 |
在一个n维空间中对传感器节点进行定位,可以看作为一个(n+1)维的矢量(ID, t1, …tr, …tn),其中:ID是n维坐标系中每个节点特有的标示符;tr是r维坐标系中传感器节点对应的坐标。为了简化模型,假设所有节点都分布在二维空间中,每个节点用(ID, x, y)来定位,且每个节点的坐标为(x, y),所有节点构成了一个无线传感器网络。
在这个无线传感器网络中,假设所有节点被随机部署在一个L×L的区域内,且所有节点都是静止的。传感器节点包括两类,一类是锚节点,这些节点可以通过全球定位系统(GPS)精确地获取自己的位置坐标;另一类是未知节点,这类节点不知道自己的位置信息。锚节点会定时广播其位置信息。
2 DV-Hop算法DV-Hop定位算法分为以下3个阶段:
1)确定未知节点与每个锚节点的最小跳数。
首先,使用典型的距离矢量交换协议,锚节点向相邻节点广播自身位置信息的分组包括跳段数,初始化为0。然后,接收节点记录到每个锚节点的最小跳数,并忽略来自于同一锚节点的较大跳数的分组,然后将跳数值加1并转发给邻居节点。通过这个方法网络中所有节点可以记录到每个锚节点的最小跳数。
2)计算未知节点与锚节点的实际跳段距离。
每个锚节点根据第一阶段中记录的其他锚节点的位置信息和相距跳数,利用下式估算平均每跳的实际距离
| $ {\rm{hopsize = }}\frac{{\sum\limits_{j \ne i} {\sqrt {{{\left( {{x_i}-{x_j}} \right)}^2} + {{\left( {{y_i}-{y_j}} \right)}^2}} } }}{{\sum\limits_{j \ne i} {{h_{ij}}} }}, $ | (1) |
其中:(xi, yi), (xj, yj)是锚节点i,j的坐标;hij是锚节点i与j(i≠j)的跳段数。
接着,锚节点将计算的平均每跳距离用带有生存期字段的分组广播到网络中,未知节点仅记录接收到的第一个每跳平均距离,并将其转发给相邻节点。
未知节点接受到平均跳距后,用平均跳距乘以第一阶段记录的最小跳数,得到了到每个锚节点之间的距离。
3)未知节点自身位置的计算。
未知节点利用记录的到各个锚节点的跳段距离值,采用三边测量法或极大似然估计法计算未知节点的坐标。
当所有锚节点到未知节点P的距离d已知时,可按式(2)进行计算
| $ \left\{ \begin{array}{l} {\left( {{x_1} - x} \right)^2} + {\left( {{y_1} - y} \right)^2} = d_1^2,\\ \;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\; \vdots \\ {\left( {{x_n} - x} \right)^2} + {\left( {{y_n} - y} \right)^2} = d_n^2. \end{array} \right. $ | (2) |
同时式(2)可以表示为
| $ \left\{ \begin{array}{l} x_1^2-x_n^2-2\left( {{x_1}-{x_n}} \right)x + y_1^2 - y_n^2 - 2\left( {{y_1} - {y_n}} \right)y\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ x_{n - 1}^2 - x_n^2 - 2\left( {{x_{n - 1}} - {x_n}} \right)x + y_{n - 1}^2 - y_n^2 - 2\left( {{y_{n - 1}} - {y_n}} \right)y = \\ d_1^2 - d_n^2, \\ \vdots \;\;\;\;\;\;\; \vdots \;\; = \\ d_{n - 1}^2 - d_n^2. \end{array} \right. $ | (3) |
式(3)的线性方程表示方式为
| $ \mathit{\boldsymbol{AX}}{\rm{ = }}\mathit{\boldsymbol{B}}, $ | (4) |
式中
| $ \begin{array}{l} \mathit{\boldsymbol{A}} = \left[{\begin{array}{*{20}{c}} {2\left( {{x_1}-{x_n}} \right)}&{2\left( {{y_1}-{y_n}} \right)}\\ \vdots & \vdots \\ {2\left( {{x_{n-1}} - {x_n}} \right)}&{2\left( {{y_{n - 1}} - {y_n}} \right)} \end{array}} \right], \\ \mathit{\boldsymbol{B = }}\left[{\begin{array}{*{20}{c}} {x_1^2-x_n^2 + y_1^2-y_n^2 + d_n^2-d_1^2}\\ \vdots \\ {x_{n - 1}^2 - x_n^2 + y_{n - 1}^2 - y_n^2 + d_n^2 - d_{n - 1}^2} \end{array}} \right], \\ \mathit{\boldsymbol{X = }}\left[\begin{array}{l} x\\ y \end{array} \right]。 \end{array} $ | (5) |
对式(4)使用标准的最小均方差估计方法得到未知节点P的坐标为
| $ \mathit{\boldsymbol{X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{-1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{B}}。 $ | (6) |
将结合RSSI测距技术对DV-Hop算法中未知节点坐标的计算方式进行改进。
RSSI测距技术[16]是根据路径损耗模型将传输损耗转化为距离,用此计算出节点间的距离。路径损耗模型通常分为两种:经验模型和理论模型。
其中,理论模型是在大量经验模型的基础上总结而成。典型的理论模型比较多,考虑到实际环境中的多径、绕射、障碍物等,通常采用如下对数-常态分布为
| $ {P_{\rm{r}}}\left( d \right) = {P_{\rm{r}}}\left( {{d_0}} \right)-10{\rm{lg}}\left( {\frac{d}{{{d_0}}}} \right) + {X_\sigma }, $ | (7) |
式中:Pr(d)是距离发射处d接收到的信号功率,即RSSI值;Pr(d0)是距离发射处d0接收到的信号功率,n为路径衰减因子;Xσ是均值为0、标准差为σ的高斯分布。在实际计算中,d0通常取1 m,Pr(d0)通常取d0为1 m处的信号强度。则上式可化简为
| $ {P_{\rm{r}}}\left( d \right) = {P_{\rm{r}}}\left( 1 \right)-10n\lg \left( d \right) + {X_\sigma }。 $ | (8) |
目前的传感器控制芯片中通常有内置的接收信号强度指示器。例如,在常用的TI公司芯片CC2430中,有
| $ RSS{I_{{\rm{VAL}}}} = {P_{\rm{r}}}\left( d \right) + RSS{I_{{\rm{OFFEST}}}}, $ | (9) |
式中,RSSIOFFEST是一个系统开发期间得到的来自前端增益的经验值,近似值为-45。RSSIVAL是从节点的RSSI寄存器读到的数据,Pr(d)是输入的RSSI强度,即节点接收到的RSSI强度。
根据公式(6)和(7),可以得出
| $ RSS{I_{{\rm{VAL}}}} = A-10n\lg d + {X_\sigma }, $ | (10) |
式中:A=P(1)+RSSIOFFEST。系数A可以通过采集数据进行拟合得到,n的取值与环境影响因子有关,根据不同建筑物的平均路径损耗指数[17],当建筑物为草地时,n取3.6,则可以根据读取的RSSIVAL算出对应的距离d。在文献[18]中,当n取3.6时,实测数据表明,10 m以内RSSI测距误差为0.5 m,15 m以内误差为2 m,超过15 m以后,RSSI的值与距离失去较好的线性。因此,相对于DV-Hop算法估测位置,在10 m以内RSSI测距技术显然更精确。
由上可知,目前的传感器节点的通信控制芯片中,通常提供有检测信号强度的方法,可以在接收数据的同时完成对RSSI的测量,无需增加额外的硬件成本。而在传感器网络的节点定位过程中,锚节点占总节点数的比例越大,则定位精度越高。基于以上考虑,对DV-Hop算法做了如下改进:
在算法的第一阶段,当所有未知节点都已经记录下到每个锚节点的最小跳数后,若未知节点到3个锚节点D1、D2、D3的一跳距离均小于10 m,则表示该未知节点位于RSSI高精度测量的范围内,根据这3个锚点的坐标利用三边测量法计算出该未知节点的位置坐标,此时,此未知节点已相当于锚节点,便可行使锚节点的功能,即升级为锚节点,再进行一次广播。
3.2 对计算出的未知节点坐标进行优化在本小节,引入“可能存在区域”以便于对计算出的未知节点坐标进行优化。
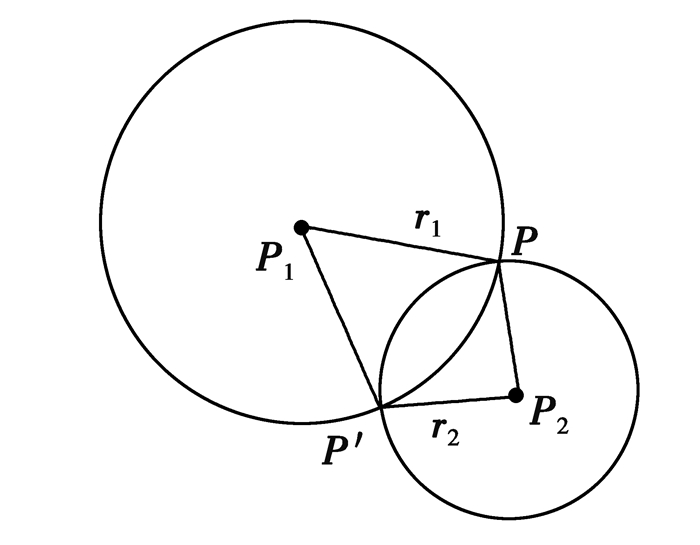
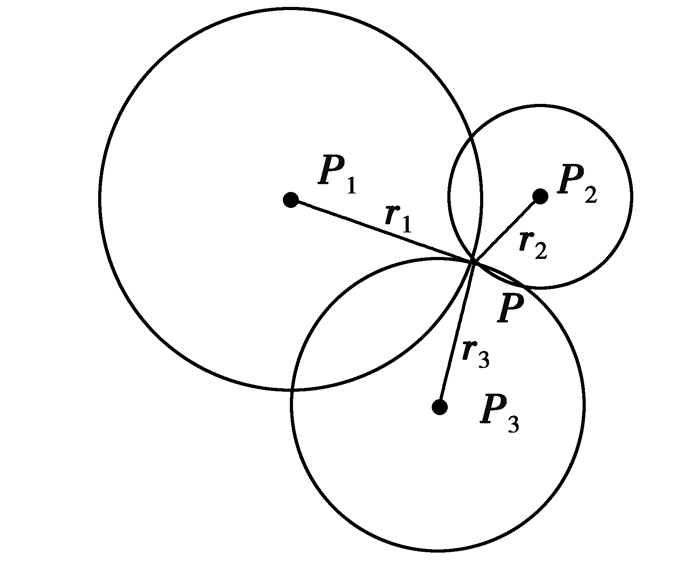
3.2.1 “可能存在区域”的定义在二维空间中节点定位可以通过节点之间的距离计算,如图 2用2个已知节点P1、P2去确定P的位置,每个节点构成一个圆,2个圆的交点有2个,不能唯一确定未知节点的位置,会产生P和P′2种情况。因此,至少需要3个已知节点P1、P2、P3才能唯一确定未知节点P的位置,如图 3所示。在定位过程中,若3个锚节点是在一条直线上的,则此时无法确定未知节点的位置。因此,在锚节点的布置和选取过程中,要尽量避免任意3个锚节点与目标节点在一条直线上,让无法定位的直线尽可能的少。虽然可以在锚节点的部署中减少此问题的出现,但是不能完全避免。
|
图 2 定位不确定性 Figure 2 Localization with uncertainty |
|
图 3 定位唯一确定性 Figure 3 Localization with unique certainty |
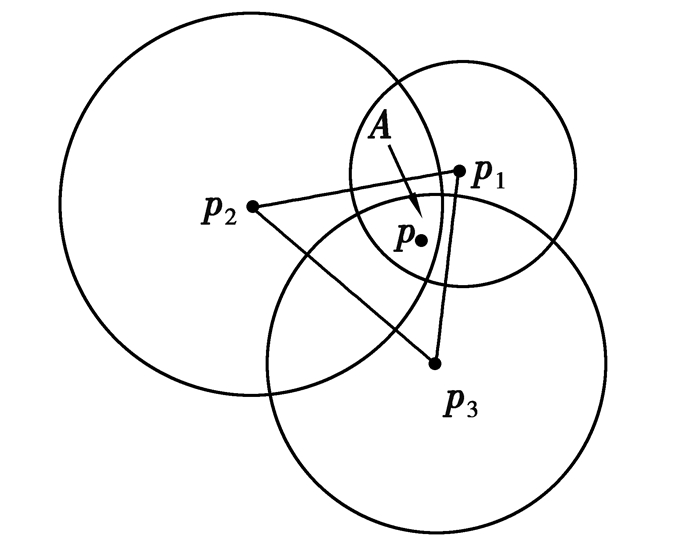
已知在二维空间中节点定位具有唯一确定性,此时节点间的距离即r1、r2、r3是固定不变的,即定位没有误差。而在实际的传感网中,定位误差是不可避免的。假定误差的范围是(0, ε),即当两个节点之间的距离为r时,定位距离的真实值范围是(r, r+ε)。图 4中3个圆围成的小区域就代表节点可能存在的位置,误差的大小就是该小区域面积的大小[19]。笔者希望在该小片区域中,找到未知节点P最可能落脚的位置。
|
图 4 带“可能存在区域”的三点定位 Figure 4 Localization with region of existence possibility |
由此,引入了“可能存在区域”的定义,即如图 4所示,3个任意半圆两两相交,3个圆重合区域是A。区域A的面积用S表示。
根据文献[19],“可能存在区域”A的面积S可表示为
| $ S = 2{\varepsilon ^2}\left( {\tan \frac{{{\alpha _{1, 2}}}}{2} + \tan \frac{{{\alpha _{2, 3}}}}{2} + \tan \frac{{{\alpha _{3, 1}}}}{2}} \right), $ | (11) |
式中:α1, 2、α2, 3、α3, 1分别ΔP1P2P3中的∠P1、∠P2、∠P3,其中,对于α1, 2、α2, 3和α3, 1有
| $ {\alpha _{1, 2}} + {\alpha _{2, 3}} + {\alpha _{3, 1}} = {\rm{ \mathsf{ π} }}{\rm{.}} $ | (12) |
ε是定位误差,
在传统DV-Hop第3阶段,未知节点通过平均每跳距离和到锚节点的估计距离之后,采用最大似然估计法进行位置估计。即对方程AX=B可用标准的最小二乘法求解X=(ATA)-1ATB。但在某些特殊情况下,逆矩阵(ATA)-1无法得到,该方法就变得无效。这些特殊情况包括:
1)在未知节点的通信半径内,有少于3个锚节点,则无法定位。
2)在未知节点的通信半径内有3个锚节点,但3个锚节点在一条直线上。
因此,使用共轭梯度法来对未知节点坐标进行优化。
共轭梯度法(conjugate gradient)是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,不仅克服了最速下降法收敛慢的缺点,而且又避免了牛顿法需要存储和计算Hessen矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性优化最有效的算法之一[20]。
以提出的“可能存在区域”A的面积S作为目标函数构建最优化问题,即
| $ f\left( {x, y} \right) = 2\left[{{{\left( {x-{x_0}} \right)}^2} + {{\left( {y-{y_0}} \right)}^2}} \right]\left( {\tan \frac{{{\alpha _{1, 2}}}}{2} + \tan \frac{{{\alpha _{2, 3}}}}{2} + \tan \frac{{{\alpha _{3, 1}}}}{2}} \right). $ | (13) |
当f(x, y) < δ时,取得最优解,δ是一个极小数,趋近于0。
采用非线性共轭梯度法求解最优解的步骤是:
步骤1:取初始值x(0)=(x0, y0),d(0)=-▽f(x(0)),精度δ>0, k=0,其中▽f(x(0))表示目标函数在点x(0)处的梯度;
步骤2:若‖▽f(x(k))‖≤δ,则算法终止,得到问题的解x(k);否则,转步骤3。
步骤3:由线性搜索确定步长αk。
步骤4:令x(k+1)=x(k)+αkd(k)。
步骤5:由
为了检验算法的性能,对DV-Hop算法和改进算法进行了仿真对比。
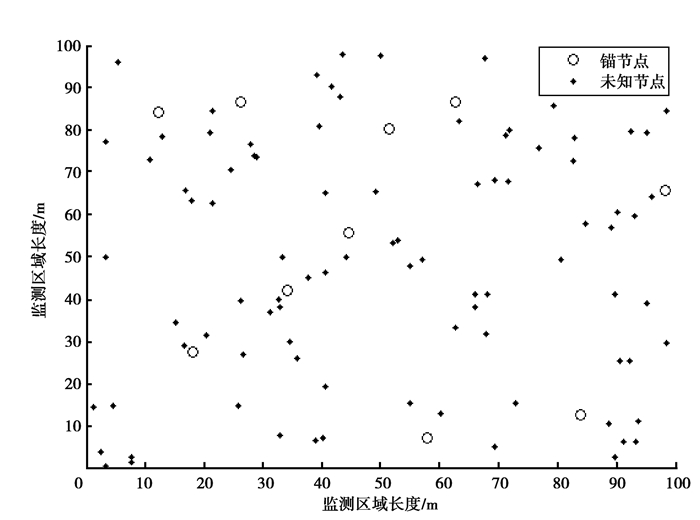
在100 m×100 m的二维区域内随机布置100个传感器节点,锚节点比例为10%,如图 5所示。每个传感器节点的通信半径为20 m,路径衰减因子n取3.6,信号发射功率为10 mW。
|
图 5 节点随机分布图 Figure 5 Random distribution diagram of nodes |
该传感网络具有以下特点:
1)所有节点部署后不再移动,每次实验仿真环境的网络区域、节点总数等网络环境参数都相同。
2)采用分簇路由协议[21],所有节点能量消耗相同。
3)锚节点已知自身信息,未知节点不知道自身信息,所有节点具有相同的能力并具有聚合数据的能力。
4)所有节点初始能量相同,并可以调整无线发射功率的大小。
5)信道符合对称性,若已知对方发射功率,节点可根据信号强度RSSI判断对方到自己的近似距离。
对于算法的性能主要从定位误差进行分析,运行算法程序50次取平均值。平均定位误差公式为
| $ {\rm{error = }}\frac{{\sum\limits_{i = m + 1}^N {\sqrt {{{\left( {x_{{\rm{est}}}^i-x_{{\rm{true}}}^i} \right)}^2} + {{\left( {y_{{\rm{est}}}^i-y_{{\rm{true}}}^i} \right)}^2}} } }}{R}, $ | (14) |
式中:(xest, yest)为节点估计坐标;(xtrue, ytrue)为节点真实坐标;m为锚节点数量;N为节点总数;R为通信半径。
如图 6所示,其中的一个点代表一个通信节点,2点间的连线代表 2个节点在彼此的通信半径范围内,可以进行通信。在非测距定位算法中,定位精度与节点分布密度相关,在节点较密集的区域,定位精度较高,在节点分布稀疏的区域,节点的可连接节点比较少,这些节点就很可能存在较大的误差。

|
图 6 节点分布网络拓扑图 Figure 6 Network topology of node distribution |
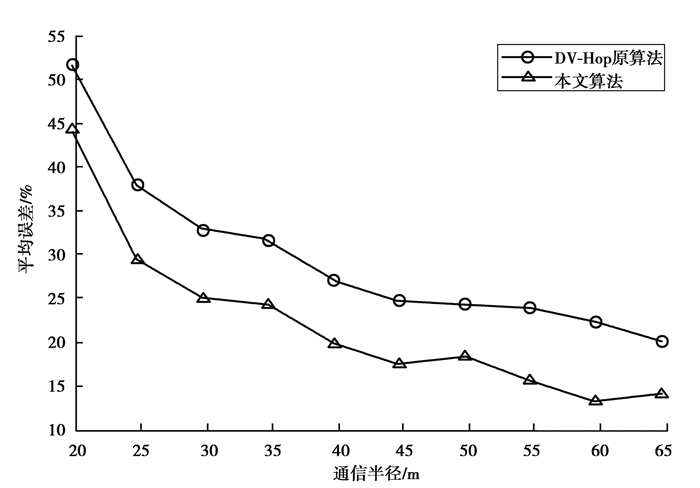
图 7比较了不同的通信半径R对定位误差的影响。将通信半径R依次选取20、25、30、35、40、45、50、55、60、65,从图中可以看出,在通信半径较小的时候,存在着更大的定位误差,例如在原算法中R为20时,定位误差为52.77%,当通信半径增大,定位误差有了明显的改善,当R为30时,定位误差已经降到33.84%。随着通信半径的增加,定位误差持续下降,而当通信半径增大到一定程度时,定位误差趋于稳定。例如在原算法中当R超过50 m后,定位误差基本稳定在25%。在本文的改进算法中,当R超过45 m时,定位误差稳定在16%。
|
图 7 定位误差与节点通信半径的关系 Figure 7 Relationship between localization errors and node communication distance |
在相同的条件下,改进算法与原算法的定位误差都随着通信半径的增大而下降,改进算法定位误差比传统DV-Hop算法的定位误差平均减小5%~10%,例如在通信半径为55 m时,原定位算法定位误差为24.76%,改进算法定位误差为16.92%,定位误差减小7.84%;当通信半径为30 m时,原算法定位误差为33.84%,改进算法定位误差为25.48%,定位误差减小8.36%。总体来说,算法的定位误差相对于原算法有明显减小,定位性能明显优于传统定位算法。
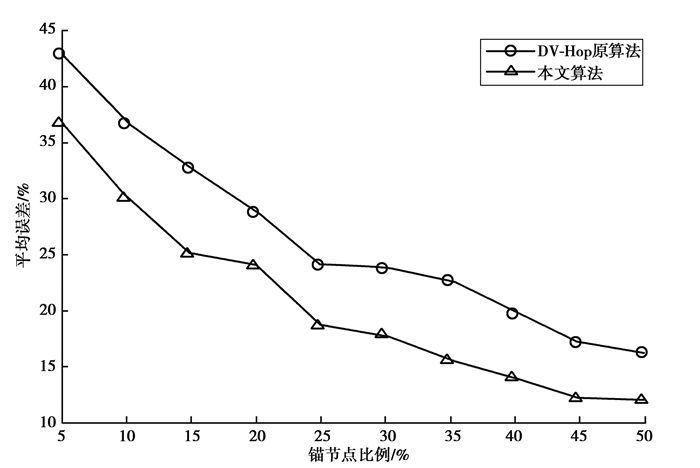
4.2.2 锚节点比例对定位误差的影响图 8是在节点数量保持不变的情况下,锚节点比例分别取0.05、0.10、0.15、0.20、0.25、0.30、0.35、0.40、0.45、0.50,通信半径R为20 m时定位误差随锚节点比例变化的曲线图。从图中可以看出,当锚节点比例较低时,定位误差更加明显。例如,当锚节点比例为5%时,原算法定位误差为42.88%。当锚节点比例增大,定位误差明显呈下降趋势,例如在原算法中,锚节点比例为10%时,定位误差下降为36.79%;当锚节点比例为15%时,定位误差降为32.73%。而当锚节点到达一定比例,定位精度趋于稳定,例如在原算法中,锚节点比例为35%时,定位误差为24.59%;锚节点比例为40%时,定位误差为19.78%;锚节点比例为45%时,定位误差为16.25%,定位误差在稳定在18%左右。
|
图 8 定位误差与锚节点比例的关系 Figure 8 Relationship between localization errors and the ratios of anchor points |
在相同仿真环境条件下,本文算法与原算法的定位误差都随着锚节点比例的增加而下降,但本文改进算法的定位误差要明显低于原DV-Hop算法,例如在锚节点比例为30%时,原算法定位误差为23.80%,本文算法定位误差为17.02%,定位误差下降6.78%;当锚节点比例为25%时,原算法定位误差为24.06%,本文算法定位误差为18.69%,定位误差下降5.37%,算法比原DV-Hop算法定位误差平均减小5%~9%,定位性能明显优于原算法。
5 结语针对无线传感器网络定位DV-Hop算法定位误差较大的问题,提出了结合RSSI定位技术的改进算法,引入非线性共轭梯度法对节点位置坐标进行优化,并详细描述了改进后的模型和算法。进而,对改进后的DV-Hop算法与原位DV-Hop算法从节点通信半径和锚节点比例两个方面对定位误差的影响进行了仿真比较和分析,仿真结果表明,在相同的网络参数下,改进后的算法定位误差平均减小了5%~10%。改进算法适用于大规模的无线传感器网络,系统的精确度和稳定性得到提高。
| [1] | Oliveira L, Li H, Almeida L, et al. RSSI-based relative localisation for mobile robots[J]. Ad Hoc Networks, 2014, 13: 321–335. DOI:10.1016/j.adhoc.2013.07.007 |
| [2] | Sahu P K, Wu E H K, Sahoo J. DuRT: dual RSSI trend based localization for wireless sensor networks[J]. Sensors Journal on IEEE, 2013, 13(8): 3115–3123. DOI:10.1109/JSEN.2013.2257731 |
| [3] | Wang Y, Ma S, Chen C L P. TOA-based passive localization in quasi-synchronous networks[J]. Communications Letters on IEEE, 2014, 18(4): 592–595. DOI:10.1109/LCOMM.2014.021214.132662 |
| [4] |
马赛, 邓冬虎, 褚一凡, 等.
基于民用移动通信信号的经典TDOA定位算法分析[J]. 现代电子技术, 2013, 36(13): 16–20.
MA Sai, DENG Donghu, CHU Yifan, et al. Analysis of classic TDOA location algorithm based on civil mobile communication signals[J]. Modern Electronics Technique, 2013, 36(13): 16–20. (in Chinese) |
| [5] | Gholami M R, Gezici S, Strom E G. Improved position estimation using hybrid TW-TOA and TDOA in cooperative networks[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3770–3785. DOI:10.1109/TSP.2012.2194705 |
| [6] | Brida P, Machaj J, Benikovsky J. Wireless sensor localization using enhanced DV-AoA algorithm[J]. Turkish Journal of Electrical Engineering and Computer Science, 2014, 22(3): 679–689. |
| [7] | Shao H J, Zhang X P, Wang Z. Efficient closed-form algorithms for AOA based self-localization of sensor nodes using auxiliary variables[J]. IEEE Transactions on Signal Processing, 2014, 62(10): 2580–2594. DOI:10.1109/TSP.2014.2314064 |
| [8] |
衣晓, 王梓有, 薛兴亮.
一种基于次锚节点的无线传感器网络质心定位算法[J]. 计算机应用与软件, 2013, 30(6): 116–120.
YI Xiao, WANG Ziyou, XUE Xingliang. A centroid localisation algorithm based on secondary anchor for wireless sensor network[J]. Computer Applications and Software, 2013, 30(6): 116–120. (in Chinese) |
| [9] | Niculescu D, Nath B. DV based positioning in ad hoc networks[J]. Telecommunication Systems, 2003, 22(1-4): 267–280. |
| [10] | Zhang A, Ye X, Hu H. Point in triangle testing based trilateration localization algorithm in wireless sensor networks[J]. KSII Transactions on Internet and Information Systems (TIIS), 2012, 6(10): 2567–2586. |
| [11] |
王颖, 石昊阳.
基于DV-Hop的无线传感器网络定位算法[J]. 仪表技术与传感器, 2012(4): 97–99.
WANG Ying, SHI Haoyang. Localization algorithm based on DV-Hop for wireless sensor networks[J]. Instrument Technique and Sensor, 2012(4): 97–99. (in Chinese) |
| [12] |
李明, 石为人.
异构传感器网络成本最优节点部署机制[J]. 重庆大学学报, 2012, 35(2): 55–59.
LI Ming, SHI Weiren. Optimal sensor deployment scheme for heterogeneous wireless sensor networks[J]. Journal of Chongqing University, 2012, 35(2): 55–59. (in Chinese) |
| [13] | Wang X S, Zhao Y J, Li H T. Improved study based on DV-Hop localization algorithm[J]. Computer Science, 2011, 38(2): 76. |
| [14] | Pan W, Liu X. Wireless sensor networks based on the DV-Hop localization algorithm[C]//Computational and Information Sciences (ICCIS), 2012 Fourth International Conference on IEEE, 2012: 1073-1075. |
| [15] | Zhang Z, Gou X, Li Y, et al. DV-hop based self-adaptive positioning in wireless sensor networks[C]//Wireless Communications, Networking and Mobile Computing, 2009. WiCom'09. 5th International Conference on IEEE, 2009: 1-4. |
| [16] | Blumrosen G, Hod B, Anker T, et al. Enhanced calibration technique for RSSI-based ranging in body area networks[J]. Ad Hoc Networks, 2013, 11(1): 555–569. DOI:10.1016/j.adhoc.2012.08.002 |
| [17] | Beck A, Eldar Y C. Strong duality in nonconvex quadratic optimization with two quadratic constraints[J]. SIAM Journal on Optimization, 2006, 17(3): 844–860. DOI:10.1137/050644471 |
| [18] |
彭建盛, 李兴, 秦志强.
三维立体空间定位算法的研究与实现[J]. 传感器与微系统, 2012, 31(7): 33–35.
PENG Jiansheng, LI Xing, QIN Zhiqiang. Research and implementation of three-dimensional spatial localization algorithm[J]. Transducer and Microsystem Technologies, 2012, 31(7): 33–35. (in Chinese) |
| [19] |
韩光洁. 智能空间中传感器网络节点精确定位与路径规划[M]. 北京: 科学出版社, 2013.
HAN Guangjie. Precise localization and path planning of wireless sensor networks in intelligent space[M]. Beijing: Science Press, 2013. (in Chinese) |
| [20] |
李董辉, 童小娇, 万中. 数值最优化算法与理论[M]. 北京: 科学出版社, 2010.
LI Donghui, TONG Xiaojiao, WANG Zhong. Numerical optimization algorithm and theory[M]. Beijing: Science Press, 2010. (in Chinese) |
| [21] |
韩万强, 刘云.
WSN中基于分簇的改进路由协议[J]. 计算机工程, 2012, 38(5): 105–107.
HAN Wanqiang, LIU Yun. Improved routing protocol based on clustering in WSN[J]. Computer Engineering, 2012, 38(5): 105–107. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38


