2. 航天恒星科技有限公司,北京 100086
2. Space Star Technology CO., LTD., Beijing 100086, P. R. China
在卫星通信和导航中,由于接收信号非常微弱,很容易受到强同频信号干扰。为此,各种抗干扰技术不断发展,比如扩频通信牺牲频带利用率抑制干扰[1],自适应阵列天线利用期望和干扰信号的空间不同特性实现抗干扰[2]。另一种抗干扰方法则是在采用极化敏感阵列前提下,利用信号和干扰不同的极化方式,即使二者波达方向相同,通过改变阵元加权系数,调整天线极化匹配因子,完成抗干扰[3]。虽然极化敏感阵列下的最优权矢量解是确定的,但可以被工程实现所采用的自适应滤波算法仍有待研究。针对卫星导航的应用环境,传统的调零天线是功率倒置准则下的LMS自适应滤波,其仅仅考虑空域特性[4]。把极化敏感阵列天线设计和传统调零天线LMS自适应滤波算法相结合,可以集合二者优点,但目前该方法的研究不够深入。该算法无需信号空间信息,具有稳健性,同时,由于每个阵元是2个自由度,抗干扰个数可以大于阵元个数。
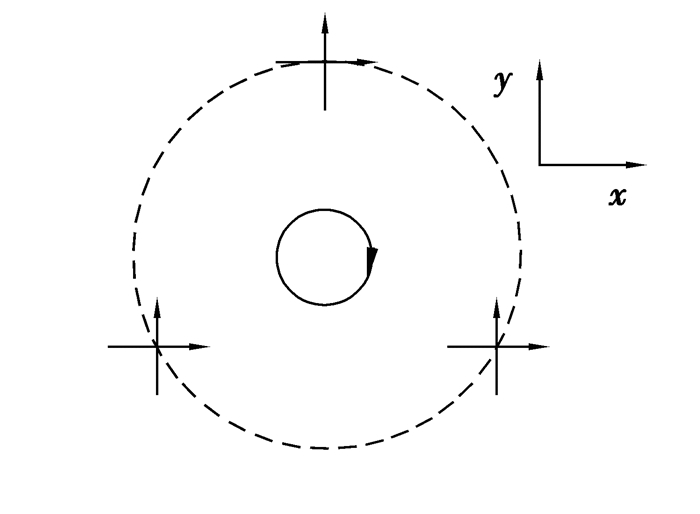
1 阵面设计阵面是由4个阵元构成的圆阵,布局如图 1所示。其中,1个阵元为右旋圆极化,位于圆心位置,其余3个阵元为正交双极化阵元,均匀分布在半径为r的圆周上。圆极化阵元接收信号作为自适应滤波的空间参考信号,之所以为右旋圆极化,是因为卫星信号是该极化方式。正交线极化阵元2个线极化分量分别与x轴和y轴平行,也可以设置为径向和圆周切向。对于前者,当多个干扰信号具有相同的方位角情况下,自由度小于后者,但为描述简单,采用x-y方向。
|
图 1 阵面布局图 Figure 1 The allocation of array antenna |
假设空间远场一电磁波入射到阵面,入射方位角、俯仰角为(φ, θ),极化参数用相位描述子为(γ, η),其原点位置电场分量为
| $ E\left( t \right) = A{{\rm{e}}^{{\rm{j}}wt}}。 $ | (1) |
根据天线基本理论,圆心位置圆极化阵元接收信号与上述电磁波关系为
| $ {r_0}\left( t \right) = E\left( t \right) \cdot {\alpha _0}{\beta _0}, $ | (2) |
式中:α0为阵元方向图因子,与信号入射角度相关;β0则是入射信号与阵元的极化匹配因子,决定于二者的极化状态和入射角度。
为了表述正交双极化阵元接收信号,首先把电场在x轴和y轴方向进行分解,此时,不考虑z轴分量情况。根据坐标变换关系,该电场分量[5]为
| $ \left[\begin{array}{l} {E_x}\\ {E_y} \end{array} \right] = E\left( t \right)\left[{\begin{array}{*{20}{c}} {-\sin \varphi }&{\cos \theta \cos \varphi }\\ {\cos \varphi }&{\cos \theta \sin \varphi } \end{array}} \right]\left[\begin{array}{l} \cos \gamma \\ \sin \gamma {e^{j\eta }} \end{array} \right] = E\left( t \right)\left[\begin{array}{l} {\beta _x}\\ {\beta _y} \end{array} \right]。 $ | (3) |
由于阵元2个极化分量为线极化,而且平行于x轴和y轴,则此时为完全匹配。但考虑到阵元并不位于圆心,电磁波到达各个阵元所经历的波程差产生相对时延,第i个阵元接收信号表示为
| $ \left[\begin{array}{l} {r_{xi}}\left( t \right)\\ {r_{yi}}\left( t \right) \end{array} \right] = E\left( t \right) \cdot {{\rm{e}}^{ - jw\tau i}} \cdot \left[\begin{array}{l} {\beta _x}\\ {\beta _y} \end{array} \right] \odot \left[\begin{array}{l} {\alpha _{xi}}\\ {\alpha _{yi}} \end{array} \right] = E\left( t \right){v_i}, $ | (4) |
式中:αxi和αyi分别为第i个阵元x方向和y方向方向图因子;βx和βy分别为极化匹配因子;τi为该阵元接收信号相对于原点信号的延时;符号⊙则表示Hadamard积。根据阵列几何位置关系,延时
| $ {\tau _i} = \frac{{{\mathit{\boldsymbol{a}}^{\rm{T}}}{\mathit{\boldsymbol{p}}_i}}}{c}, $ | (5) |
式中:c为光速;pi为阵元i的坐标矢量;a为信号入射角度定义的单位矢量,即
| $ {\mathit{\boldsymbol{p}}_i} = {\left[{\begin{array}{*{20}{c}} {{p_{xi}}}&{{p_{yi}}}&{{p_{zi}}} \end{array}} \right]^{\rm{T}}}, $ | (6) |
| $ \mathit{\boldsymbol{a = }}{\left[{\begin{array}{*{20}{c}} {-\sin \theta \cos \varphi }&{-\sin \theta \sin \varphi }&{-\cos \varphi } \end{array}} \right]^{\rm{T}}}。 $ | (7) |
对于卫星导航应用,具有如下一些特点:一是信号链路是空空或者空地,无需考虑多径影响;二是接收信号中,卫星信号经过扩频以后,功率往往比噪声还小20 dB,可以忽略,相反,干扰信号由于传播距离短,功率远高于噪声[6]。借鉴空域滤波中的功率倒置准则,可以把该算法应用于极化自适应抗干扰天线中。
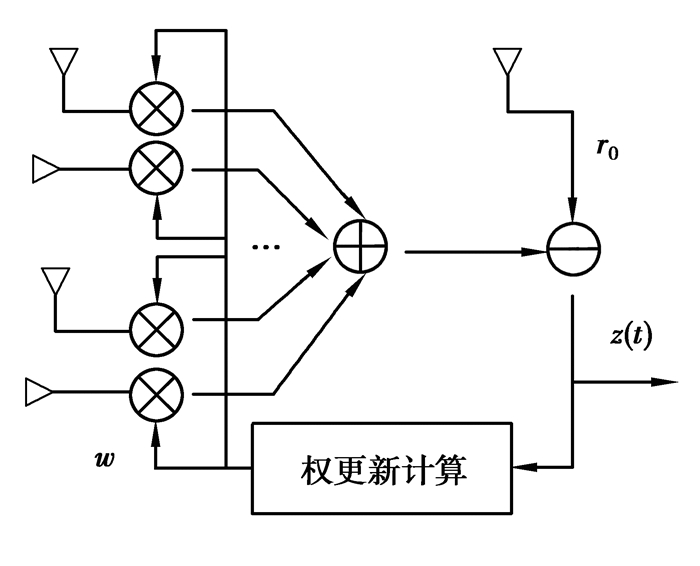
3.2 功率倒置准则阵列虽然仅仅包含4个阵元,但由于正交线极化阵元有2个馈点,实际接收信号为7路。把圆极化阵元接收的信号作为参考信号d(t),加权因子约束为1,通过调整其他6个权值构成的矢量w,并进行加权求和,使得参考信号与合成信号之差功率最小,即与输入信号功率成“倒置”状态。系统结构如图 2所示。
|
图 2 系统框图 Figure 2 Diagram of system |
定义输入信号矢量
| $ \mathit{\boldsymbol{r = }}{\left[{\begin{array}{*{20}{c}} {{r_{x1}}}&{{r_{y1}}}&{{r_{x2}}}&{{r_{y2}}}&{{r_{x3}}} \end{array}} \right]^{\rm{T}}} = E\left( t \right)\mathit{\boldsymbol{v, }} $ | (8) |
矢量v是一个由方向图、极化、信号波达方向和阵元位置决定的矢量,为
| $ \mathit{\boldsymbol{v = }}{\left[{\begin{array}{*{20}{c}} {{v_{1x}}}&{{v_{1y}}}&{{v_{2x}}}&{{v_{2y}}}&{{v_{3x}}} \end{array}} \right]^{\rm{T}}}。 $ | (9) |
干扰抑制后的输出为
| $ z\left( t \right) = d\left( t \right)-{\mathit{\boldsymbol{w}}^{\rm{H}}}\left( t \right)r\left( t \right), $ | (10) |
其中
| $ d\left( t \right) = {r_0}\left( t \right), $ | (11) |
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_w \left\{ {z{z^{\rm{H}}}} \right\}, \\ s.t.\left\| w \right\| = 1. \end{array} \right. $ | (12) |
最优权矢量为
| $ {\mathit{\boldsymbol{w}}_{opt}} = {\left[{\begin{array}{*{20}{c}} {{w_{x1}}}& \cdots &{{w_{y3}}} \end{array}} \right]^{\rm{T}}} = \mu {\mathit{\boldsymbol{R}}^{ -1}}{\mathit{\boldsymbol{v}}_0}, $ | (13) |
其中,μ为常数;R为接收信号协方差矩阵;v0为如式(9)定义的期望信号方向矢量。
3.3 权矢量计算方法根据最优权矢量表达式,由于存在矩阵求逆运算,采用直接矩阵求逆的开环自适算法实现并不现实。而由于导航中干扰信号远大于期望信号的条件,可以采用LMS自适应滤波算法。LMS算法虽然收敛速度有限,但实现非常简单,稳态误差也可以通过调整步长参数进行优化。算法迭代计算方法为
| $ \mathit{\boldsymbol{w}}\left( {k + 1} \right) = \mathit{\boldsymbol{w}}\left( k \right) + \kappa {z^*}\left( k \right)r\left( k \right)。 $ | (14) |
算法实现步骤为:
第一步,设置步长κ和权矢量初始值w(0);
第二步,根据当前输入信号快拍,按照式(10)计算该时刻的误差信号,即阵列输出z(k);
第三步,按照式(14)进行权矢量更新;
第四步,重复执行第二步和第三步,得到阵列输出z(k)。
根据LMS自适应滤波算法基本理论,上述实现方法的性能主要包括收敛时间和稳态误差。迭代步长越大,收敛越快,稳态误差越大;干扰功率越大,收敛越快,输出失调越大,即输出信号z(k)功率越大。需要特别指出,虽然干扰功率大时,z(k)功率增加,但z(k)的干噪比却比小功率信号时更小。原因在于,实际情况下参考信号本身包括了噪声,即
| $ d\left( t \right) = {r_0}\left( t \right) + n\left( t \right), $ | (15) |
干扰功率大时,参考信号更为准确。所以,干扰功率越大,自适应抗干扰天线对干扰抑制效果越好。
3.4 权矢量对天线极化影响根据权矢量和算法实现方法,把式(2)、(8)代入到式(10),可得阵列输出为
| $ z\left( t \right) = E\left( t \right){\alpha _0}{\beta _0}-E\left( t \right){\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{v, }} $ | (16) |
由于方向矢量
| $ \mathit{\boldsymbol{v = }}\left[\begin{array}{l} {\alpha _{x1}}\\ {\alpha _{y1}}\\ {\alpha _{x2}}\\ {\alpha _{y2}}\\ {\alpha _{x3}}\\ {\alpha _{y3}} \end{array} \right] \times \left[\begin{array}{l} {\beta _x}\\ {\beta _y}\\ {\beta _x}\\ {\beta _y}\\ {\beta _x}\\ {\beta _y} \end{array} \right] \times \left[\begin{array}{l} {e^{-jw\tau 1}}\\ {e^{-jw\tau 1}}\\ {e^{-jw\tau 2}}\\ {e^{ - jw\tau 2}}\\ {e^{ - jw\tau 3}}\\ {e^{ - jw\tau 3}} \end{array} \right], $ | (17) |
为了分析天线极化状态,假设各个阵元均是全向天线,则
| $ {\alpha _{xi}} = {\alpha _{\beta i}} = {\alpha _0} = 1, $ | (18) |
式(16)可以进一步化简为
| $ z\left( t \right) = E\left( t \right)\left[{{\beta _0}-\sum\limits_{i = 1}^3 {{{\rm{e}}^{-jw\tau i}}\left( {w_{xi}^*{\beta _{xi}} + w_{yi}^*{\beta _{yi}}} \right)} } \right]。 $ | (19) |
根据天线基本理论[9],上式中的第二个因子为该阵列天线的等效极化因子,即
| $ \rho = {\beta _0}-\sum\limits_{i = 1}^3 {{{\rm{e}}^{-jw\tau i}}\left( {w_{xi}^*{\beta _{xi}} + w_{yi}^*{\beta _{yi}}} \right)} 。 $ | (20) |
从该表达式可以看出,极化匹配因子同诸多因素有关,包括阵元极化匹配因子,信号波达方向,权矢量取值。通过调整权矢量,就可以改变等效极化匹配因子,进而等效改变阵列在信号波达方向上的等效极化状态。
4 仿真和实验假设GPS导航信号采用L1频段[9],即1 575.42 MHz,阵列布局如图 1所示,阵列半径等于信号半波长,卫星信号的SNR为-30 dB,方位角和俯仰角分别为(100°, 30°)。空间存在干扰信号,方位角和俯仰角分别为(100°, 30°)、(250°, 70°),干扰信号INR分别为20 dB和25 dB,极化方式分别为线极化和圆极化,为了不形成相干信号,载频分别取1 574.42 MHz和1 576.42 MHz。算法采用所述的基于功率倒置准则的LMS自适应滤波算法,无需信号波达方向信息,中心阵元信号作为参考信号。
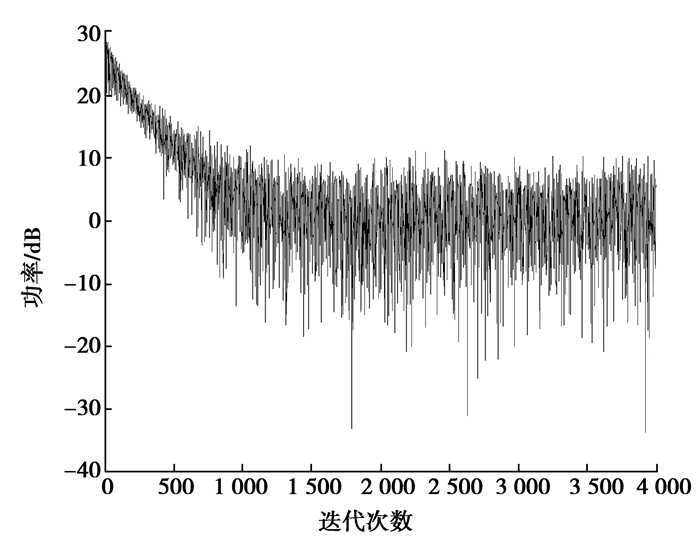
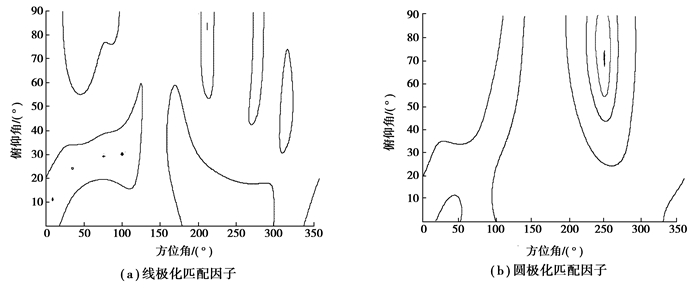
图 3展示了迭代过程中,输出信号z(t)的瞬时功率变化曲线,图 4则是收敛后,阵列等效极化匹配因子曲线,图 4(a)对应线极化,而图 4(b)对应圆极化。图中可以看出,收敛后的信号能量接近噪声功率,说明干扰信号得到了有效抑制。而匹配因子在角度等于干扰信号角度的位置,是一个非常小的值,说明阵列通过控制不同角度极化状态,实现干扰抑制。而在期望信号角度(100°, 30°)上,线极化出现了零点而圆极化没有,说明线极化干扰被抑制,而圆极化期望信号被保留。
|
图 3 2个干扰时输出信号瞬时功率 Figure 3 The instantaneous power of the output signal in the case of 2 jams |
|
图 4 2个干扰时等效极化匹配因子图 Figure 4 The equivalent polarimetric match factor in the case of 2 jams |
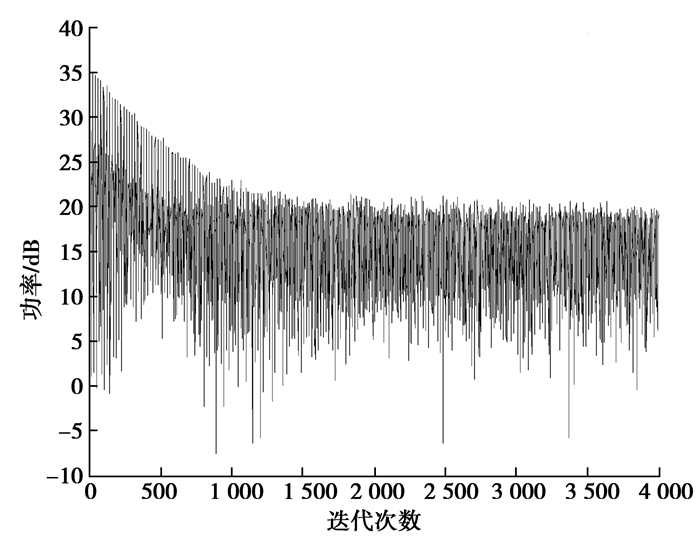
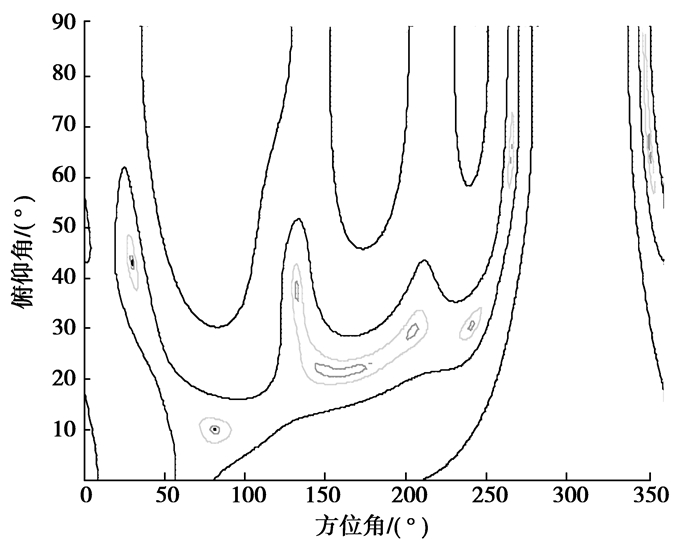
采用阵列有6个自由度,最多可以抗6个干扰,大于阵元个数。仿真假设空间存在6个干扰,极化均为线极化,所有干扰INR均等于20 dB,信号频率彼此相差500 kHz,范围为1 574.42~1 576.92 MHz。干扰信号角度分别为(80°, 10°)、(160°, 20°)、(240°, 30°)、(30°, 40°)、(200°, 30°)、(350°, 70°)。同样采用功率倒置准则下的LMS算法,输出信号z(t)瞬时功率曲线和收敛后的等效极化匹配因子分别如图 5和图 6所示。从图 5可以看出,相对于2个干扰情况,由于信号多,协方差矩阵非零特征值多,收敛后的失调较大,即输出信号功率较大[10]。但图 6表明,在干扰信号角度,极化匹配因子远小于1,干扰得到了抑制,阵列可以抗6个干扰。另外,由于图 6仅仅是在1 575.42 MHz频点的图形,所以,某些角度同设置并不完全一致。
|
图 5 6个干扰时输出信号瞬时功率 Figure 5 The instantaneous power of the output signalin the case of 6 jams |
|
图 6 6个干扰时等效极化匹配因子图 Figure 6 The equivalent polarimetric match factorin the case of 6 jams |
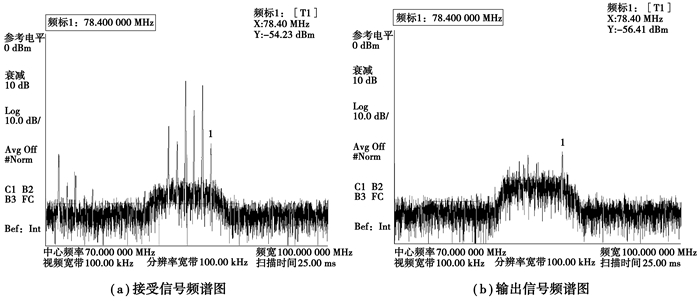
在进行仿真的同时进行了实际测试,通过频谱仪的测试结果如图 7所示。干扰信号为6个不同圆极化点频信号,从不同方向入射阵面。其中,图 7(a)为阵面接收到的中频信号频谱图,图 7(b)为经自适应滤波后输出的中频信号频谱图。对比两图可以看出干扰信号得到了有效抑制,验证了空域极化域联合抗干扰调零天线的抗干扰性能。相对于单个干扰信号50 dB动态,从图 7(b)可以看出有部分干扰信号残留,此时的干扰信号动态范围有所下降,能够达到40 dB。
|
图 7 实测的6个干扰时中频信号频谱图 Figure 7 The measured spectrum of IF signalin the case of 6 jams |
针对卫星导航和卫星通信的抗干扰要求,设计了4阵元阵列。阵元为正交双极化,算法采用功率倒置准则的LMS自适应滤波。从理论分析和实验结果可以看出,新算法结合了空域和极化域资源,提高了天线自由度,使得4个阵元天线可以抗6个干扰。
| [1] |
杨小牛, 楼才义, 徐建良. 软件无线电原理与应用[M]. 北京: 电子工业出版社, 2001: 23-55.
YANG Xiaoniu, LOU Caiyi, XU Jianliang. Software radio principle and application[M]. Beijing: electronic industry press, 2001: 23-55. (in Chinese) |
| [2] | Ulversoy T. Software defined radio: challenges and opportunities[J]. IEEE Communications Surveys & Tutorials, 2010, 12(4): 531–550. |
| [3] | Chastellain F, Botteron C, Farine P. Looking inside modern receivers[J]. IEEE Microwave Magazine, 2011, 12(2): 87–98. DOI:10.1109/MMM.2010.940105 |
| [4] | Zeng W, Wang L, Wang Y, et al. Joint polarized and spatial domain anti-jamming method for GNSS[C]//Signal Processing, Communication and Computing (ICSPCC), 2013 IEEE International Conference on.[s. n.]: IEEE, 2013:1-5. |
| [5] | Munoz-Ferreras J M, Gómez-García R, Pérez-Martínez F. RF front-end concept and implementation for direct sampling of multiband signals[J]. Circuits & Systems II Express Briefs IEEE Transactions on, 2011, 58(3): 129–133. |
| [6] | Psiaki M L, Powell S P, Jung H, et al. Design and practical implementation of multifrequency RF front ends using direct RF sampling[J]. IEEE Transactions on Microwave Theory & Techniques, 2005, 53(10): 3082–3089. |
| [7] | Li Q, Wang W, Xu D, et al. A robust anti-jamming navigation receiver with antenna array and gps/sins[J]. IEEE Communications Letters, 2014, 18(3): 467–470. DOI:10.1109/LCOMM.2014.012314.132451 |
| [8] |
蔺晓龙, 何文涛, 徐建华, 等.
卫星导航接收机中窄带干扰抑制算法[J]. 计算机仿真, 2014, 31(1): 72–75.
LIN Xiaolong, HE Wentao, XU Jianhua, et al. An improved gps receiver anti-jammer algorithm based on space-time adaptive processing[J]. Computer Simulation, 2014, 31(1): 72–75. (in Chinese) |
| [9] |
郭崇贤. 相控阵雷达接收技术[M]. 北京: 国防工业出版社, 2009.
GUO Chongxian. Phased array radar receiver technology[M]. Beijing: National Defence Industry Press, 2009. (in Chinese) |
| [10] | Wang T, Wang D, Hurst P J, et al. A level-crossing analog-to-digital converter with triangular dither[J]. IEEE Transactions on Circuits and Systems, 2009, 56(9): 2089–2099. DOI:10.1109/TCSI.2008.2011586 |
 2015, Vol. 38
2015, Vol. 38

