高炉炼铁工艺是冶金工业中最为重要的工艺之一,炉内多种相态共同存在、物理化学现象交错耦合,单靠传统的经验预测的方式已经无法满足目前炼铁工艺的发展需求。通过建立数学模型来模拟高炉内部现象的技术不仅能对实际生产中的高炉冶炼状态进行精细、有效地预报和反映,而且能够对高炉炼铁新工艺的研发提供有效的指导。因此,对高炉内状态进行建模和仿真十分必要[1-2]。
网格生成(grids-generation)技术是数值模拟过程中重要的前处理过程,是模拟计算的先决条件[3-7]。模型的求解以网格为框架,所有的物理量都是在此网格上进行离散和求解的,网格的质量直接影响模型计算的精度和效率以及方程计算的收敛性。因此,网格质量的好坏对高炉数学模型的求解意义重大[8-9]。目前,在各类网格生成方法中,通过求解偏微分方程获得的适体坐标(body-fitted coordinates,BFC)网格的方法应用最为广泛。与传统的直角网格相比,通过计算的方法来构造的适体坐标系能够与模拟区域的不规则边界更好地适应,取得更好的模拟结果,并且在达到同等精度的条件下,适体坐标网格生成技术所需网格量少,计算时间短并且对计算机内存容量的要求更低[10]。目前,在高炉数学模拟中,对高炉区域BFC网格生成技术的研究还很少。笔者采用椭圆型微分方程法,以Matlab软件作为平台,对适用于高炉数学模型的网格生成程序进行了研究和开发,以期为高炉数学模型的发展做出贡献。
1 BFC网格生成技术 1.1 概述BFC网格生成技术其实是一种将物理平面上的不规则区域转变成计算平面上的规则区域的坐标转换方法,坐标系中计算平面的点和物理平面的点一一对应。由于实际求解区域多为不规则区域,利用BFC网格生成法可以将偏微分方程的离散转移到矩形网格上,从而在很大程度上降低计算难度。BFC网格的生成大致可分为3大类:代数变换法、保角变换法(又称复变函数法)和微分方程变换法。
微分方程变化法是目前应用最为广泛的BFC网格生成方法[4],通过求解这组方程获得物理平面和计算平面内部节点之间的对应关系,从而将不规则的物理区域转变成规则的计算区域。其中,椭圆型偏微分方程法应用最广,该法适应性好,生成的网格质量高、稳定,文中采用椭圆型偏微分方程法来生成BFC网格。
1.2 网格的疏密和正交性控制优质的网格应该能够根据变化的剧烈程度来控制网格的疏密,计算区域中变化剧烈处网格较密,变化缓慢处网格较疏,合理分布网格的疏密能够提高计算精度,并且节省计算资源。除此之外,网格还要具有较好的正交性,尤其是边界处的网格正交性,较好的正交性便于控制方程边界条件的设置,提高控制方程准确性。
为了改善所生成网格的性能,对网格的疏密度和正交性进行控制,在拉普拉斯方程的基础上增加源项P、Q,即通过求解泊松方程来生成BFC网格。通过选取合适的源项,能够有效地改善网格的质量。设(x, y)为物理平面坐标系,(ξ, η)为计算平面坐标系,计算平面坐标系到物理平面坐标系的变换关系采用的泊松方程为
| $ \left\{ \begin{align} &\frac{{{\partial }^{2}}\xi }{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}\xi }{\partial {{y}^{2}}}=P\left(\xi, \eta \right), \\ &\frac{{{\partial }^{2}}\eta }{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}\eta }{\partial {{y}^{2}}}=Q\left(\xi, \eta \right).\\ \end{align} \right. $ | (1) |
泊松方程法在提出后得到了广泛的应用,同时,研究人员也开发出了多种源项控制函数的构造方法。文中采用魏文礼等[11-15]建立的计算形式,为
| $ \left\{ \begin{align} &P\left(x, y \right)=\phi/\left[{{\left(\frac{\partial x}{\partial \xi } \right)}^{2}}+{{\left(\frac{\partial y}{\partial \xi } \right)}^{2}} \right], \\ &Q\left(x, y \right)=\psi/\left[{{\left(\frac{\partial x}{\partial \eta } \right)}^{2}}+{{\left(\frac{\partial y}{\partial \eta } \right)}^{2}} \right], \\ \end{align} \right. $ | (2) |
式中,边界上的ϕ,ψ的计算公式为
| $ \left\{ \begin{align} &\phi=-\frac{\frac{\partial x}{\partial \xi }\frac{{{\partial }^{2}}x}{\partial {{\xi }^{2}}}+\frac{\partial y}{\partial \xi }\frac{{{\partial }^{2}}y}{\partial {{\xi }^{2}}}}{{{\left(\frac{\partial x}{\partial \xi } \right)}^{2}}+{{\left(\frac{\partial y}{\partial \xi } \right)}^{2}}}+\frac{\frac{\partial x}{\partial \xi }\frac{{{\partial }^{2}}x}{\partial {{\eta }^{2}}}+\frac{\partial y}{\partial \xi }\frac{{{\partial }^{2}}y}{\partial {{\eta }^{2}}}}{{{\left(\frac{\partial x}{\partial \eta } \right)}^{2}}+{{\left(\frac{\partial y}{\partial \eta } \right)}^{2}}}, \\ &\psi=-\frac{\frac{\partial x}{\partial \eta }\frac{{{\partial }^{2}}x}{\partial {{\eta }^{2}}}+\frac{\partial y}{\partial \eta }\frac{{{\partial }^{2}}y}{\partial {{\eta }^{2}}}}{{{\left(\frac{\partial x}{\partial \eta } \right)}^{2}}+{{\left(\frac{\partial y}{\partial \eta } \right)}^{2}}}+\frac{\frac{\partial x}{\partial \eta }\frac{{{\partial }^{2}}x}{\partial {{\xi }^{2}}}+\frac{\partial y}{\partial \eta }\frac{{{\partial }^{2}}y}{\partial {{\xi }^{2}}}}{{{\left(\frac{\partial x}{\partial \xi } \right)}^{2}}+{{\left(\frac{\partial y}{\partial \xi } \right)}^{2}}}.\\ \end{align} \right. $ | (3) |
求得边界上的ϕ,ψ后,通过线性插值的方法得到内部各节点的ϕ,ψ值,进而获得各节点的源项值P、Q。
2 高炉求解区域的划分采用微分方程变换法划分BFC网格时,需要设定方程的第一类边界条件,即物理平面和计算平面在边界上的坐标对应关系。对于高炉求解区域,首先要确定4条逻辑边界,文中将高炉料面作为上边界,炉缸内渣面为下边界,高炉中轴线作为左边界,炉壁作为右边界,然后再确定需要划分的网格数和边界上的节点坐标。边界上节点坐标的确定有等间距法、等角度法、等差数列等多种方法,根据高炉4条逻辑边界的具体情况采用不同的方法确定节点坐标。
需要指出的是,在高炉数学模型中,死料区仅气、液两相可以通过,下降到该区域的固相只能沿其表面向风口回旋区运动,因此,死料区的上边界也要作为控制方程求解的边界条件。为了便于求解,网格走向需要沿着死料区的边界,即将死料区边界也作为一条逻辑边界。高炉物理平面和计算平面的对应关系如图 1所示。
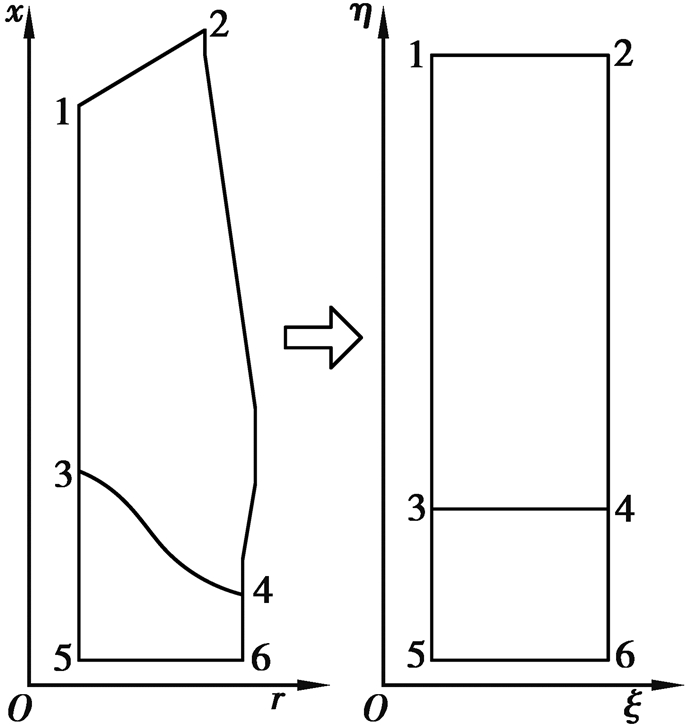
|
图 1 高炉物理平面和计算平面的对应关系 Figure 1 The Schematic diagram ofrelationship between the Blast Furnacephysical plane and the computing plane |
由于高炉求解区域为单连通区域,并且逻辑边界是比较规则的平面,因此,采用等间距法确定边界上的坐标即可满足要求。高炉料面和出铁口为规则的平面,根据需要划分的网格数,直接采用等间距法确定边界坐标值。死料区边界3-4将高炉分为两个区域,并将逻辑边界1-5和逻辑边界2-6分为上下两个部分,由于划分网格数的不同,两个部分需要单独采用等间距法确定边界坐标值。因此,在确定边界条件前,要先确定高炉的死料区边界的位置。
根据矶部浩一等[16]的试验结果和理论分析,死料区的表面轮廓可表示为
| $ \frac{\text{d}r}{\text{d}x}=\tan \left(\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+0.5\times {{\tan }^{-1}}\left(0.8271\times \frac{r}{R} \right)\right). $ | (4) |
式中:r,x分别为料面点的径向坐标和轴向坐标,m;R为炉缸半径,m。
3 BFC网格的求解 3.1 椭圆型方程的转换泊松方程需要在物理平面(x, y)内求解偏微分方程和其边界条件构成的定解问题,但是物理平面的边界是任意的,不规则边界的泊松方程求解是很困难的,因此,将泊松方程反变换至计算平面(ξ, η)进行求解。泊松方程反变换后的方程为
| $ \left\{ \begin{align} &\alpha \frac{{{\partial }^{2}}x}{\partial {{\xi }^{2}}}-2\beta \frac{{{\partial }^{2}}x}{\partial \xi \partial \eta }+\gamma \frac{{{\partial }^{2}}x}{\partial {{\eta }^{2}}}=-{{J}^{2}}\left(P\frac{\partial x}{\partial \xi }+Q\frac{\partial x}{\partial \eta } \right), \\ &\alpha \frac{{{\partial }^{2}}y}{\partial {{\xi }^{2}}}-2\beta \frac{{{\partial }^{2}}y}{\partial \xi \partial \eta }+\gamma \frac{{{\partial }^{2}}y}{\partial {{\eta }^{2}}}=-{{J}^{2}}\left(P\frac{\partial y}{\partial \xi }+Q\frac{\partial y}{\partial \eta } \right), \\ \end{align} \right. $ | (5) |
式中,
| $ \left\{ \begin{align} &J=\frac{\partial x}{\partial \xi }\frac{\partial x}{\partial \eta }-\frac{\partial x}{\partial \eta }\frac{\partial y}{\partial \xi }, \\ &\alpha={{\left(\frac{\partial x}{\partial \eta } \right)}^{2}}+{{\left(\frac{\partial y}{\partial \eta } \right)}^{2}}, \\ &\beta=\frac{\partial x}{\partial \xi }\frac{\partial x}{\partial \eta }-\frac{\partial y}{\partial \xi }\frac{\partial y}{\partial \eta }, \\ &\gamma={{\left(\frac{\partial x}{\partial \xi } \right)}^{2}}+{{\left(\frac{\partial y}{\partial \xi } \right)}^{2}}.\\ \end{align} \right. $ | (6) |
采用“中心差分法”对主方程(5)、(6)进行离散,网格节点按从左至右、从上至下进行编号。设定δξ=δη=1,整理得到x(i, j)和y(i, j)的迭代格式为
| $ x\left( {i,j} \right) = \frac{1}{{2\left[ {\alpha \left( {i,j} \right) + \gamma \left( {i,j} \right)} \right]}}\left\{ \begin{array}{l} \alpha \left( {i,j} \right)\left[ {x\left( {i + 1,J} \right) + x\left( {i - 1,j} \right)} \right] - \\ \frac{{\beta \left( {i,j} \right)}}{2}\left[ \begin{array}{l} x\left( {i + 1,j - 1} \right) - x\left( {i + 1,j + 1} \right)\\ + x\left( {i - 1,j + 1} \right) - x\left( {i - 1,j - 1} \right) \end{array} \right] + \\ \gamma \left( {i,j} \right)\left[ {x\left( {i,j - 1} \right) + x\left( {i,j + 1} \right)} \right] + \\ \frac{1}{2}{J^2}\left( {i,j} \right)\frac{{\varphi \left( {i,j} \right)}}{{\gamma \left( {i,j} \right)}}\left[ {x\left( {i + 1,j} \right) - x\left( {i - 1,j} \right)} \right] + \\ \frac{1}{2}{J^2}\left( {i,j} \right)\frac{{\psi \left( {i,j} \right)}}{{\alpha \left( {i,j} \right)}}\left[ {x\left( {i,j - 1} \right) - x\left( {i,j + 1} \right)} \right] \end{array} \right\}, $ | (7) |
| $ y\left( {i,j} \right) = \frac{1}{{2\left[ {\alpha \left( {i,j} \right) + \gamma \left( {i,j} \right)} \right]}}\left\{ \begin{array}{l} \alpha \left( {i,j} \right)\left[ {y\left( {i + 1,J} \right) + y\left( {i - 1,j} \right)} \right] - \\ \frac{{\beta \left( {i,j} \right)}}{2}\left[ \begin{array}{l} y\left( {i + 1,j - 1} \right) - y\left( {i + 1,j + 1} \right) + \\ y\left( {i - 1,j + 1} \right) - y\left( {i - 1,j - 1} \right) \end{array} \right] + \\ \gamma \left( {i,j} \right)\left[ {y\left( {i,j - 1} \right) + y\left( {i,j + 1} \right)} \right] + \\ \frac{1}{2}{J^2}\left( {i,j} \right)\frac{{\varphi \left( {i,j} \right)}}{{\gamma \left( {i,j} \right)}}\left[ {y\left( {i + 1,j} \right) - y\left( {i - 1,j} \right)} \right] + \\ \frac{1}{2}{J^2}\left( {i,j} \right)\frac{{\psi \left( {i,j} \right)}}{{\alpha \left( {i,j} \right)}}\left[ {y\left( {i,j - 1} \right) - y\left( {i,j + 1} \right)} \right] \end{array} \right\}, $ | (8) |
其中,
| $ \left\{ \begin{align} &\alpha \left(i, j \right)=0.25\times {{\left[x\left(i, j-1 \right)-x\left(i, j+1 \right)\right]}^{2}}+0.25\times {{\left[y\left(i, j-1 \right)-y\left(i, j+1 \right)\right]}^{2}}, \\ &\beta \left(i, j \right)=0.25\times \left[x\left(i+1, j \right)-x\left(i-1, j \right)\right]\times \left[x\left(i, j-1 \right)-x\left(i, j+1 \right)\right]+\\ &\ \ \ \ \ \ \ \ \ \ \ \ \ 0.25\times \left[y\left(i+1, j \right)-y\left(i-1, j \right)\right]\times \left[y\left(i, j-1 \right)-y\left(i, j+1 \right)\right], \\ &\gamma \left(i, j \right)=0.25\times {{\left[x\left(i+1, j \right)-x\left(i-1, j \right)\right]}^{2}}+0.25\times {{\left[y\left(i+1, j \right)-y\left(i-1, j \right)\right]}^{2}}, \\ &J\left(i, j \right)=0.25\times \left[x\left(i+1, j \right)-x\left(i-1, j \right)\right]\times \left[y\left(i, j-1 \right)-y\left(i, j+1 \right)\right]- \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ 0.25\times \left[x\left(i, j-1 \right)-x\left(i, j+1 \right)\right]\times \left[y\left(i+1, j \right)-y\left(i-1, j \right)\right].\\ \end{align} \right. $ | (9) |
由式(2)可知,计算P、Q,首先要计算ϕ、ψ值。根据边界上设定的坐标对应关系,计算边界上的ϕ、ψ值,进而根据边界上的ϕ、ψ值线性插值得到中间节点的ϕ、ψ值。根据式(2)得到各节点P、Q的值,有
| $ \left\{ \begin{align} &P\left(i, j \right)=\frac{4\times \phi \left(i, j \right)}{{{\left[x\left(i+1, j \right)-x\left(i-1, j \right)\right]}^{2}}+{{\left[y\left(i+1, j \right)-y\left(i-1, j \right)\right]}^{2}}}, \\ &Q\left(i, j \right)=\frac{4\times \psi \left(i, j \right)}{{{\left[x\left(i, j-1 \right)-x\left(i, j+1 \right)\right]}^{2}}+{{\left[y\left(i+1, j \right)-y\left(i-1, j \right)\right]}^{2}}}.\\ \end{align} \right. $ | (10) |
计算程序用MATLAB编制,程序流程图如图 2所示。设定的网格点数为16×71=1 136,迭代精度为10-5。
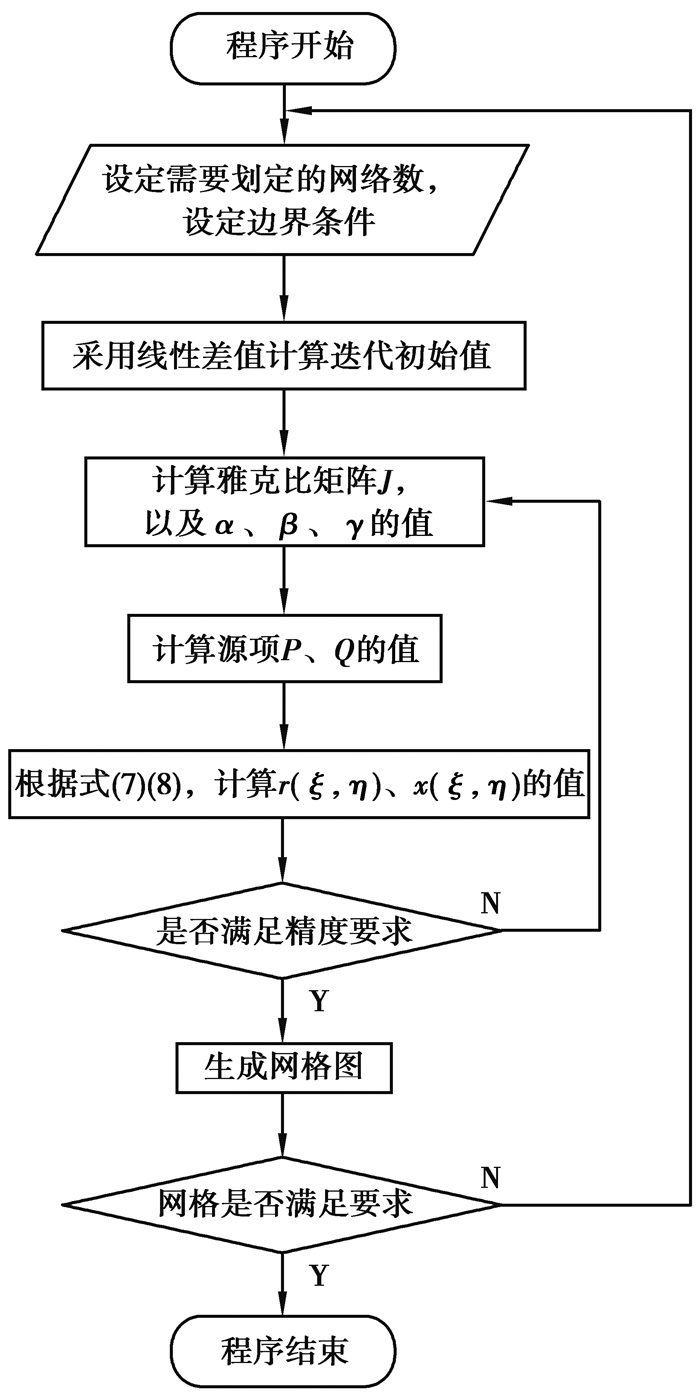
|
图 2 BFC网格生成流程图 Figure 2 The flowchart of BFC Grid generation |
算例所参考的炉型结构为:炉喉半径3.5 m;炉腰半径5.45 m;炉缸半径4.875 m;炉喉高1.85 m;炉身高15.3 m;炉腰高2 m;渣面到炉腰底部5 m;渣面到风口中心2 m;风口回旋区深度1.13 m。根据文中提出的方法,对料面到渣面之间的高炉的数值模拟区域进行适体坐标系网格的生成,结果令人满意。如图 3所示,网格内点和边界处的网格线正交性良好,计算速度和收敛速度也比较快,生成的网格能够满足高炉数学模型的要求。
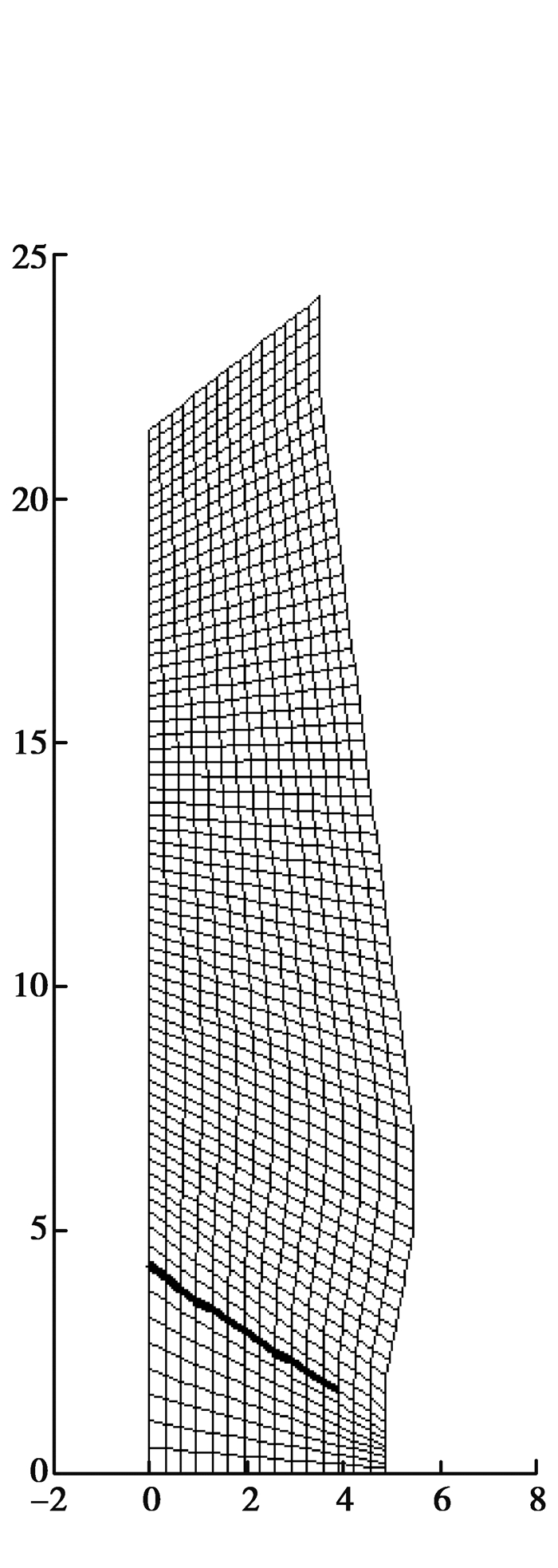
|
图 3 高炉模拟区域的BFC网格 Figure 3 The BFC grid of BlastFurnace simulation zone |
在高炉数学模型BFC网格生成过程中,首先根据死料区边界的计算结果将高炉计算区域分为两个部分,高炉数学模型中涉及的反应主要分布在死料区边界上方部分,而死料区边界下方部分涉及的反应较少,因此死料区边界下方的网格较上方稀疏一些。计算时,死料区边界也作为椭圆方程求解时的边界条件,两部分分别生成BFC网格,在处理两部分区域连接断面时, 将已计算出的分区曲线网格的边界断面作为下一个分区的边界条件处理,保证了整个网格的连续性。
5 结语生成BFC网格是高炉数学模型前处理的重要组成部分,合格的BFC网格不仅能够有效提高数学模型的求解精度,提高求解效率,而且还能够加速方程的收敛。文中采用椭圆型方程变换法生成BFC网格,在划分求解区域时,除了料线、墙体、渣面和中心轴线等边界之外,还将死料区的轮廓作为BFC网格计算的边界条件,以简化数学模型的求解过程。采用带有源项的泊松方程作为变换方程,网格的正交性和疏密程度便于控制,结合具体的算例可以看出,该网格生成算法原理简单,易于编程,网格生成效率高,并且收敛性好,生成的网格能够满足高炉数学模型求解的要求。
| [1] |
储满生, 郭宪臻, 沈峰满, 等.
多流体高炉数学模型的开发和应用[J]. 钢铁, 2007, 42(12): 11–15.
ZHU Mansheng, GUO Xianzhen, SHEN Fengman, et al. Development and application of the blast furnace mathematical model more fluid[J]. Iron and Steel, 2007, 42(12): 11–15. (in Chinese) |
| [2] |
史岩彬.基于CFD/NHT分析技术的高炉炼铁过程建模与仿真研究[D].济南:山东大学, 2006. SHI Yanbin.Study based on CFD/NHT analysis technology of blast furnace ironmaking process modeling and simulation[D].Jinan:Shandong University, 2006.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10422-2006168680.htm |
| [3] |
阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006.
YAN Chao. Computational fluid dynamics method and its application[M]. Beijing: Beijing University of Aeronautics and Astronautics press, 2006. (in Chinese) |
| [4] |
陶文栓. 计算传热学的近代进展[M]. 北京: 科学出版社, 2000.
TAO Wenshuan. Recent progress of computational heat transfer[M]. Beijing: Science Press, 2000. (in Chinese) |
| [5] |
李林波, 曾文斌, 朱军, 等.
CFD数值模拟技术在冶金中的应用[J]. 钢铁研究学报, 2011, 23(12): 1–4.
LI Linbo, ZENG Wenbin, ZHU Jun, et al. CFD numerical simulation technology application in metallurgy[J]. Journal of Iron and Steel Research, 2011, 23(12): 1–4. (in Chinese) |
| [6] |
刘厚林, 董亮, 王勇, 等.
流体机械CFD中的网格生成方法进展[J]. 流体机械, 2010, 38(4): 32–37, 22.
LIU Houlin, DONG Liang, WANG Yong, et al. Fluid machinery CFD method of grid generation progress[J]. Journal of Fluid Mechanics, 2010, 38(4): 32–37, 22. (in Chinese) |
| [7] |
张志荣, 冉景煜, 张力, 等.
内燃机缸内气体CFD瞬态分析中动态网格划分技术[J]. 重庆大学学报, 2005, 28(11): 97–100.
ZHANG Zhirong, RAN Jingyi, ZHANG Li, et al. Gas in cylinder of internal combustion engine in the CFD transient analysis dynamic meshing technique[J]. Journal of Chongqing University, 2005, 28(11): 97–100. (in Chinese) |
| [8] |
张潮.贴体坐标转换在河冰模拟中的应用研究[D].合肥:合肥工业大学, 2007. ZHANG Chao.Stick put oneself in coordinate transformation in the application of the river ice simulation study[D].Hefei:Hefei University of Technology, 2007.(in Chinese) http://www.cnki.com.cn/Article/CJFDTOTAL-BCDT201206011.htm |
| [9] |
茅泽育, 张磊, 王永填, 等.
采用适体坐标变换方法数值模拟天然河道河冰过程[J]. 冰川冻土, 2003, 25(S2): 214–219.
MAO Zeyu, ZHANG Lei, WANGN Yongtian, et al. Adopt suitable body coordinate transformation method for numerical simulation of river river ice process[J]. Journal of Ice Frozen Soil, 2003, 25(S2): 214–219. (in Chinese) |
| [10] | Thompson J F, Thames F C, Martin C W. Automatic numerical generation of body-fitted curvilinear coordinate system for field containing any number of arbitrary two dimensional bodies[J]. Journal of Computational Physics, 1974, 15: 299–319. DOI:10.1016/0021-9991(74)90114-4 |
| [11] |
魏文礼, 王玲玲, 金忠青.
曲线网格生成技术研究[J]. 河海大学学报, 1998, 26(3): 92–96.
WEI Wenli, WANG Lingling, JIN Zhongqing. Curve grid generation technology research[J]. Journal of Hohai University, 1998, 26(3): 92–96. (in Chinese) |
| [12] |
何红雨, 保宗悌.
方形同轴电位数值计算的MATLAB实现[J]. 云南师范大学学报:自然科学版, 2003, 23(4): 42–46.
HE Hongyu, BAO Zongti. Square coaxial potential numerical calculation of MATLAB[J]. Journal of Yunnan Normal University:natural science, 2003, 23(4): 42–46. (in Chinese) |
| [13] |
王军, 张潮, 倪晋.
二维贴体网格生成方法[J]. 合肥工业大学学报, 2006, 23(12): 1549–1551.
WANG Jun, ZHANG Chao, NI Jin. Stick put oneself in two-dimensional grid generation method[J]. Journal of Hefei University of Technology, 2006, 23(12): 1549–1551. (in Chinese) |
| [14] |
蒋丽丽, 孙建国.
基于Poisson方程的曲网格生成技术[J]. 世界地质, 2008, 30(5): 298–305.
JIANG Lili, SUN Jianguo. Based on Poisson equation curve grid generation technique[J]. Geology in the world, 2008, 30(5): 298–305. (in Chinese) |
| [15] | Brown P R. A interactive method for the automatic genetation of finite element meshes using the Schwarz-Christoffel transformation[J]. Computer Methods in Applied Mechanics and Engineering, 1981, 25(1): 101–126. DOI:10.1016/0045-7825(81)90071-2 |
| [16] | 矶部浩一, 桑守原, 鞭岩. 高炉下部における固体粒子运动のシミュレーション[J]. 铁と钢, 1981, 67(4): S53. |
 2015, Vol. 38
2015, Vol. 38


