细小颗粒通过填充介质的渗流行为是工业生产中常见的物理现象,在诸如粉末技术、药物学、农业甚至钢铁冶金等行业中扮演重要角色。其中,高炉炼铁过程炉身上部较小球团矿/烧结矿渗流进入大颗粒焦炭层的运动行为已引起学者们的关注[1-3]。而另一新兴炼铁工艺COREX的炉顶布料过程[4-6],炉内物料下行[7]等固相运动过程均包括多元尺寸颗粒的混合,细小颗粒在填充大颗粒中自发的渗流行为则是颗粒混合过程中常见的现象。渗流行为的发生可一定程影响床层的整体运动状态,例如床层中某一区域渗流作用强烈,颗粒高温发粘引起的表面摩擦系数增大等可导致渗流颗粒在床层空隙中沉积堵塞,降低该区域的空隙度,影响气流分布和物料运动。因此,为探索COREX过程中渗流颗粒的运动行为特别是其上部竖炉的渗流沉积现象,有必要对填充床中细小颗粒的渗流行为进行基础性研究,为下一步的研究提供相应的理论依据。
根据填充床中细小颗粒渗流行为的研究方法,可将其分成两大类:物理实验研究和数值模拟。Bridgwate等[8-9]通过物理实验研究了细小颗粒的渗流速度、停留时间、径向扩散等的渗流行为。Li[10]、Richard等[11]利用蒙特卡洛法描述细小颗粒的渗流行为。而近年来,随着计算机能力的大幅提升,基于拉格朗日坐标系考虑颗粒与颗粒/壁面相互作用的离散单元法(DEM)可从颗粒尺度描述细小颗粒在填充床中的渗流行为,已引起学者的广泛关注[12-15]。笔者采用离散单元法建立填充床中细小颗粒渗流的数学模型,考察不同颗粒直径比、不同阻尼系数、不同滑动摩擦系数条件下细小颗粒的渗流速度、停留时间、径向扩散、运动轨迹等信息。
1 数学模型 1.1 DEM模型的建立细小颗粒在填充床渗流过程中,颗粒受自身重力及颗粒与颗粒/壁面之间作用力,同时,颗粒还受到切向力扭矩和滚动摩擦扭矩作用,使颗粒产生平移运动和转动。根据牛顿第二定律,颗粒运动的控制方程可描述为
| $ {m_i}\frac{{({\rm{d}}{v_i})}}{{{\rm{d}}t}} = \sum\limits_{j = 1}^{ki} {({F_{{\rm{cn, }}ij}} + {F_{{\rm{dn, }}ij}} + {F_{{\rm{ct, }}ij}} + {F_{{\rm{dt, }}ij}}) + {m_i}g}, $ | (1) |
| $ {\boldsymbol{I}_i}\frac{{{\rm{d}}{\omega _i}}}{{{\rm{d}}t}} = \sum\limits_{j = 1}^{ki} {({\boldsymbol{T}_{ij}} + {\boldsymbol{M}_{ij}}), } $ | (2) |
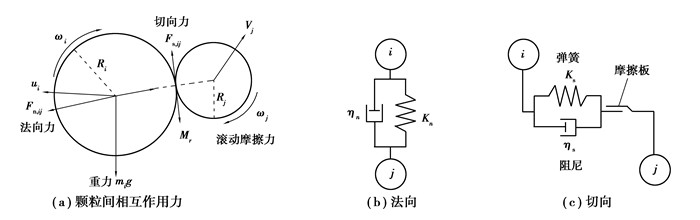
式中:mi为颗粒i的质量,kg;Ii为转动惯量,kg·m2;vi为平动速度,m/s;ωi为转动速度,r/s;mig为i颗粒所受重力;Fcn, ij,Fct, ij为颗粒间法向、切向接触力,N;Fdn, ij,Fdt, ij为颗粒间法向、切向阻尼力,N;Tij,Mij分别为颗粒所受切向力扭矩和滚动摩擦扭矩,N·m;ki为与i颗粒相接触颗粒数目。本文颗粒间相互作用力模型采用如图 1所示的线性“弹簧-阻尼-摩擦板”模型。颗粒所受接触力、阻尼力、摩擦力及扭矩如表 1所示[4, 6, 7, 16]。
|
图 1 颗粒间相互作用力模型 Figure 1 Model of interaction force between two particles |
| 表 1 i颗粒所受作用力及力矩 Table 1 Forces and torques of particle i |
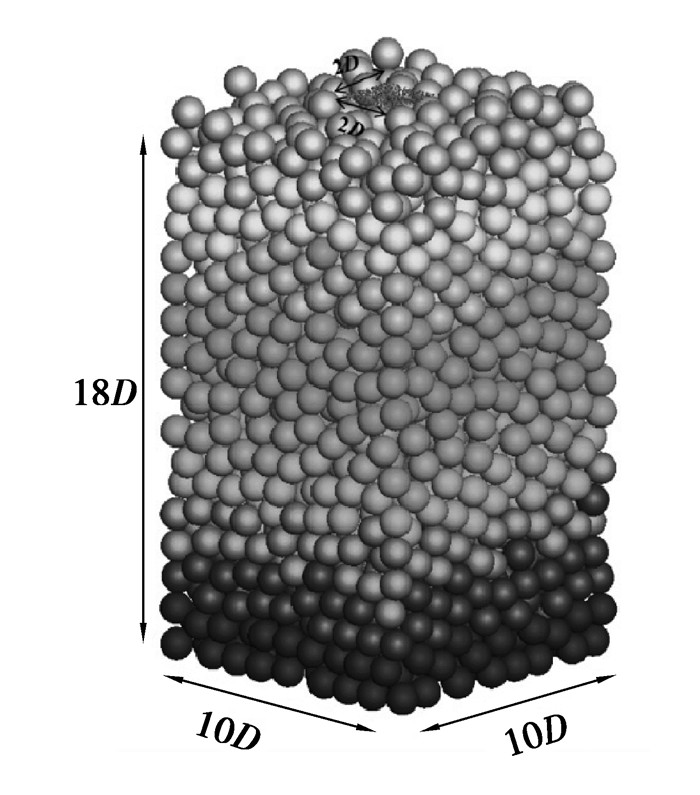
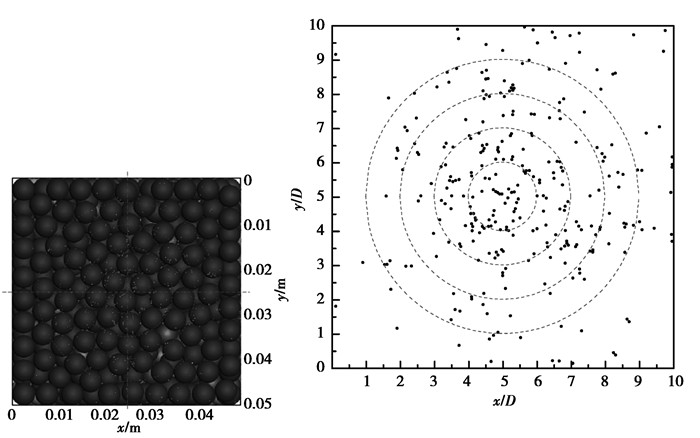
本模型为10D×10D×18D的矩形填充床,如图 2所示。填充床中初始堆积直径D的填充颗粒,当填充床层形成后渗流小颗粒在床层顶部中心2D×2D矩形框中形成。细小颗粒在重力作用下渗流通过填充床到达床层底部。本模型中填充颗粒和渗流小颗粒拥有相同的物理性质,同时,颗粒墙之间的碰撞与颗颗粒之间的碰撞一致,只是墙不会产生位移。模拟参数如表 2所示。
|
图 2 填充床几何结构图 Figure 2 Geometry of the packed bed |
| 表 2 模拟参数 Table 2 Simulation parameters |
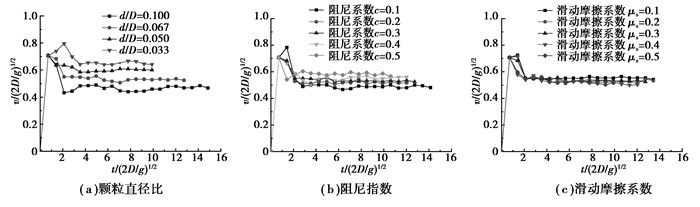
图 3为不同模拟参数下细小颗粒的平均渗流速度。由图 3可知,不同参数条件下,细小颗粒穿过填充床层呈现相同规律。在模拟开始阶段,由于细小颗粒的自由落体运动,颗粒速度迅速增加。当细小颗粒进入填充床后,渗流颗粒与填充颗粒发生碰撞并沿床层空隙向下运动,其渗流速度降低并逐渐达到稳定状态。学者们[9, 12-14]通过物理模拟和数值分析亦发现细小颗粒通过随机排列填充床时其渗流速度为一定值。图 3(a)为颗粒直径比对渗流速度的影响,随着颗粒直径比的减小,渗流速度逐渐增加。主要原因是大颗粒直径比会增加渗流颗粒与填充颗粒的碰撞频率,增加渗流颗粒下降的阻力,从而导致渗流速度的降低。图 3(b)为阻尼系数对细小颗粒渗流速度的影响,由图可知,随着阻尼系数的减小,细小颗粒渗流速度逐渐减小。该现象可解释为在颗粒杨氏模量确定条件下,阻尼系数的减小反应颗粒恢复系数的增大,因此,较小阻尼系数条件下,渗流颗粒与填充颗粒碰撞前后的速度改变量较小,渗流颗粒易于在床层径向上发展,导致竖直方向的渗流速度减小。图 3(c)为不同滑动摩擦系数下颗粒渗流速度的变化。由图可知滑动摩擦系数对细小颗粒的渗流速度影响较小。滑动摩擦系数对颗粒运动的影响主要体现在当颗粒间相互接触并作用相当长时间时,对颗粒运动的平移动能及线性动量的改变,而渗流过程中,细小颗粒与填充颗粒相互碰撞后立即弹开,相互接触作用时间短,因此, 滑动摩擦系数对细小颗粒的渗流速度影响较小。
|
图 3 不同模拟参数下细小颗粒平均渗流速度 Figure 3 The mean percolation velocity of percolating particles under different simulation parameters |
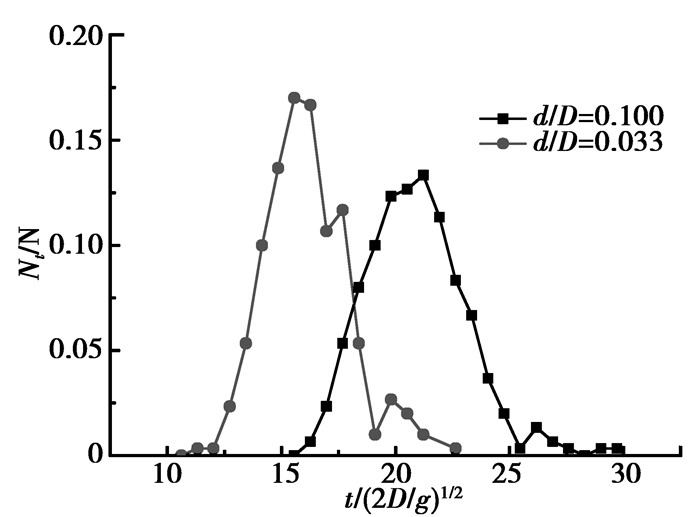
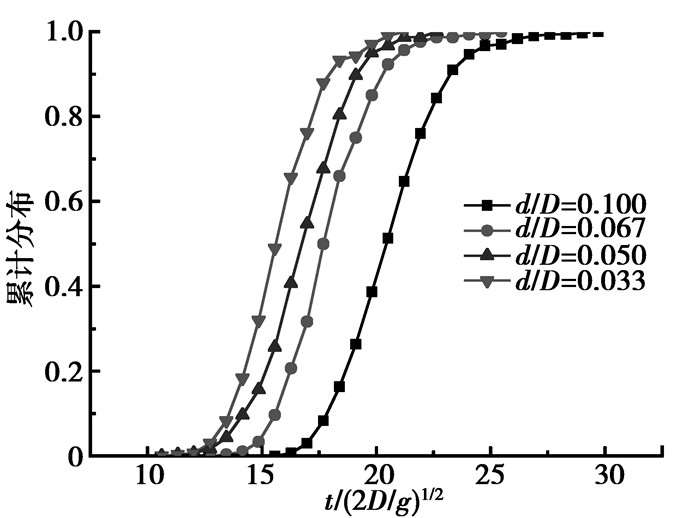
细小颗粒的停留时间分布是描述其在填充床中渗流行为的重要特征参数。Bridgwater等[9]物理实验发现细小颗粒渗流过程中的停留时间分布类似于正态分布。相同的趋势同样可在本文中得到,如图 4所示。由图 4可知,随着颗粒直径比的增大,停留时间分布曲线向右移动,分布变宽。主要原因是大的颗粒直径比,细小颗粒的渗流速度变小,颗粒需要更长时间到达床层底部。图 5为不同直径比下细小颗粒的累计停留时间分布,随着颗粒直径比的增大,累计停留时间分布曲线向右移动,细小颗粒的平均停留时间逐渐增长。
|
图 4 不同颗粒直径比下停留时间分布 Figure 4 Distributions of residence time for different diameter ratios of percolating to packing particles |
|
图 5 不同颗粒直径比下累计停留时间分布 Figure 5 Cumulative distribution of residence time for different diameter ratios of percolating to packing particles |
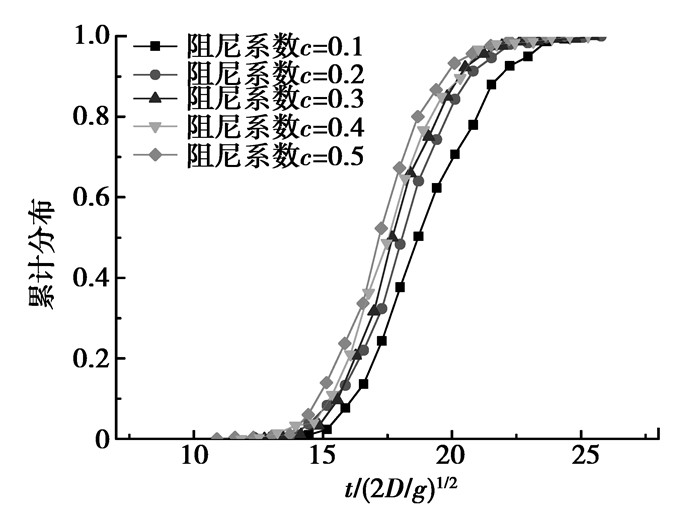
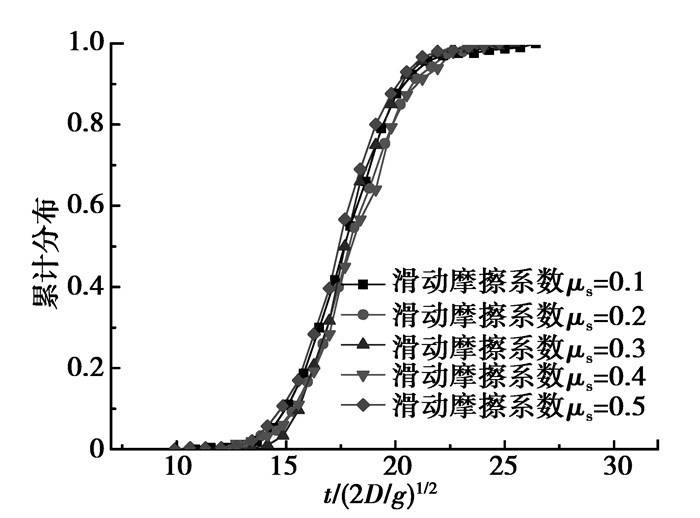
图 6为不同阻尼系数下细小颗粒的累计停留时间分布,由图可知,随着阻尼系数的增大,细小颗粒的累计停留时间分布向左移动,主要是由于阻尼系数的增大,颗粒渗流速度逐渐增大,颗粒在床层中停留时间变小。图 7为不同滑动摩擦系数下细小颗粒的累计停留时间分布,由于渗流过程中滑动摩擦系数对颗粒的平移动能及线性动量影响较小,因此, 不同滑动摩擦系数时,细小颗粒在床层中的停留时间相差不大。
|
图 6 不同阻尼系数下累计停留时间分布 Figure 6 Cumulative distribution of residence time for different damping coefficients |
|
图 7 不同滑动摩擦系数下累计停留时间分布 Figure 7 Cumulative distribution of residence time for different sliding friction coefficients |
渗流过程中细小颗粒的径向弥散是一个较为复杂的运动过程。Bridgwater等[8]通过物理实验提出了描述颗粒径向弥散的理论模型,可描述为
| $ \frac{r}{{4{E_{\rm{r}}}t}} = \ln \left( {\frac{N}{{N-{N_{\rm{r}}}}}} \right), $ | (3) |
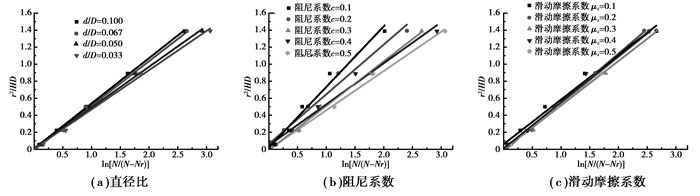
式中:Er为径向弥散系数;r为床层中心半径;t为时间;N为细小颗粒总数;Nr为t时刻距床层中心r内细小颗粒数量。渗流过程细小颗粒径向弥散的示意图如图 8所示。图 9(a)为不同直径比下细小颗粒的径向弥散。由图可知,随颗粒直径比的增加,径向弥散程度增大。主要原因是随着颗粒直径比的增大,细小颗粒通过床层空隙的相对通道面积变小,细小颗粒与填充颗粒碰撞的频率增加,细小颗粒趋于径向运动,所以其径向弥散程度增大。
|
图 8 径向弥散示意图 Figure 8 Schematic diagram of the radial dispersion |
|
图 9 不同参数下细小颗粒的径向弥散 Figure 9 The radial dispersion of percolating particles under different simulation parameters |
图 9(b)为阻尼系数对细小颗粒径向弥散的影响。由图可知,随着阻尼系数的变小,细小颗粒的径向弥散逐渐变大。主要原因是颗粒间阻尼系数直接影响颗粒间的阻尼力,而阻尼力的主要作用是消除颗粒间的相对动能。渗流过程中,细小颗粒在重力作用下向下运动穿透床层,细小颗粒与填充颗粒碰撞过程会引起相对速度的改变,而颗粒间的相互阻尼力直接影响速度改变量的大小。因此,较小的阻尼系数,引起颗粒间相对速度变化小,细小颗粒趋于向径向方向发展,其径向弥散程度变大。滑动摩擦系数对细小颗粒径向弥散的影响如图 9(c)所示。由于渗流过程中颗粒间的相互接触时间较短,滑动摩擦系数对细小颗粒的径向弥散影响较小。
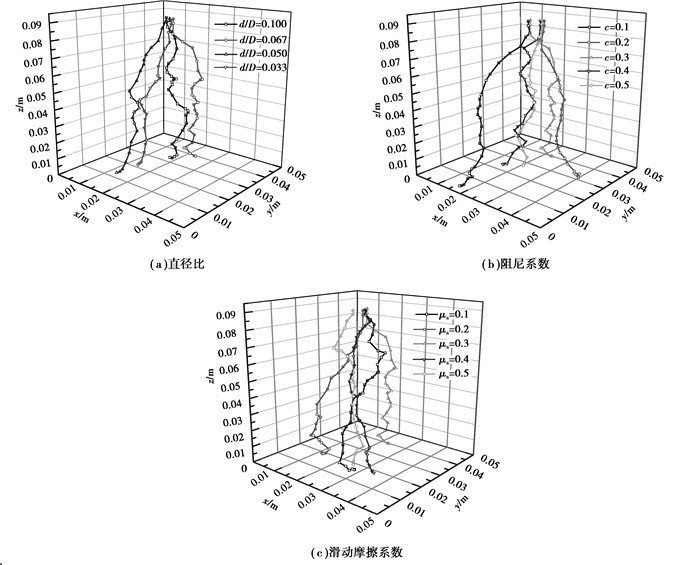
2.4 渗流颗粒运动轨迹DEM模拟方法可从颗粒尺寸角度描述渗流过程中的运动信息,例如可精确得到细小颗粒在填充床中的运动轨迹。图 10为不同操作条件下,某一渗流颗粒在填充床中的运动轨迹。本文描述颗粒轨迹为其停留时间等于该模拟条件平均停留时间时的颗粒。图 10(a)为不同直径比下渗流颗粒的运动轨迹。d/D=0.1时,渗流颗粒平均停留时间最长,从图 10(a)可看出,该颗粒运动轨迹出现急剧变化的转角,导致该颗粒的停留时间变长,主要原因是由于渗流颗粒直径变大,颗粒在空隙下降过程时会在某些细小空隙中缓慢移动,甚至趋于静止并沉积在填充介质中,因此, 渗流颗粒的停留时间会变长。图 10(b)为不同阻尼系数下渗流颗粒的运动轨迹。由图 10(b)可知,随着阻尼系数的减小,细小颗粒趋于向床层边缘运动,颗粒偏离床层中心程度变大,渗流颗粒在床层中运动路程增大,这也可解释随着颗粒间阻尼系数的降低,渗流颗粒停留时间变长。图 10(c)为滑动摩擦系数对渗流颗粒运动轨迹的影响。由于滑动摩擦系数对渗流过程中渗流颗粒的运动行为影响较小,所以, 相同停留时间条件下,不同滑动摩擦系数时,渗流颗粒的差别不大,颗粒偏离中心距离亦相差不大。
|
图 10 不同模拟参数下渗流颗粒运动轨迹 Figure 10 The trajectory of a percolating particle under different simulation parameters |
对填充床中细小颗粒渗流行为进行了DEM模拟,考察了不同模拟参数对渗流速度、停留时间、径向弥散等渗流行为的影响,特别是对颗粒的运动轨迹进行了描述。模拟结果如下:
1) 渗流过程中细小颗粒的平均渗流速度为一定值。随着颗粒直径比的增加,颗粒平均渗流速度逐渐减小,停留时间逐渐增加,颗粒的径向弥散逐渐增加。
2) 随着颗粒间阻尼系数的增加,颗粒渗流速度逐渐增加,停留时间逐渐减小,径向弥散逐渐变小。滑动摩擦系数对细小颗粒的渗流行为影响较小。
3) 颗粒直径比d/D=0.1时,颗粒运动轨迹出现急剧变化的转角,颗粒的停留时间变长,颗粒在某些细小空隙中缓慢移动,甚至趋于静止,易导致颗粒沉积行为的发生。
4) 随着颗粒间阻尼系数变小,颗粒运动轨迹向填充床边缘发展,偏离床层中心, 渗流颗粒在床层中运动路程增大。滑动摩擦系数对细小颗粒渗流过程的运动轨迹影响不大。
| [1] | Kajiwara Y, Inada T, Tanaka T. Two dimensional analysis on the formation process of burden distribution at blast furnace top[J]. Transactions of the Iron and Steel Institute of Japan, 1988, 28(11): 916–925. DOI:10.2355/isijinternational1966.28.916 |
| [2] | Yu Y W, Westerlund A, Paananen T, et al. Inter-particle percolation segregation during burden descent in the blast furnace[J]. ISIJ International, 2011, 51(7): 1050–1056. DOI:10.2355/isijinternational.51.1050 |
| [3] | Yu Y W, Saxén H. Effect of DEM parameters on the simulated inter-particle percolation of pellets into coke during burden descent in the blast furnace[J]. ISIJ International, 2012, 52(5): 788–796. DOI:10.2355/isijinternational.52.788 |
| [4] | Li H F, Luo Z G, Zou Z S, et al. Mathematical simulation of burden distribution in COREX melter gasifier by discrete element method[J]. Journal of Iron and Steel Research, International, 2012, 19(9): 36–42. DOI:10.1016/S1006-706X(13)60006-0 |
| [5] | Kou M Y, Wu S L, Du K P, et al. DEM simulation of burden distribution in the upper part of COREX shaft furnace[J]. ISIJ international, 2013, 53(6): 1002–1009. DOI:10.2355/isijinternational.53.1002 |
| [6] | Li Q, Feng M X, Zou Z S. Validation and calibration approach for discrete element simulation of burden charging in pre-reduction shaft furnace of COREX process[J]. ISIJ International, 2013, 53(8): 1365–1371. DOI:10.2355/isijinternational.53.1365 |
| [7] | Han L H, Luo Z G, Zhou H, et al. Influence of cohesive zone shape on solid flow in COREX melter gasifier by discrete element method[J]. Journal of Iron and Steel Research, International, 2015, 22(4): 304–310. DOI:10.1016/S1006-706X(15)30004-2 |
| [8] | Bridgwater J, Sharpe N W, Stocker D C. Particle mixing by percolation[J]. Transactions of the Institution of Chemical Engineers, 1969, 47: 114–119. |
| [9] | Bridgwater J, Ingram N D. Rate of spontaneous inter-particle percolation[J]. Transactions of the Institution of Chemical Engineers, 1971, 49: 163–169. |
| [10] | Li J Z.Computer simulation of particle packing and percolation[D].Sydney:The University of New South Wales, 1998. |
| [11] | Richard P, Oger L, Lemaȋtre J, et al. Application of the Voronotessellation to study transport and segregation of grains inside 2D and 3D packings of spheres[J]. Granular Matter, 1999, 1(4): 203–211. DOI:10.1007/s100350050026 |
| [12] | Lominé F, Oger L. Transport of small particles through a 3D packing of spheres:experimental and numerical approaches[J]. Journal of Statistical Mechanics:Theory and Experiment, 2006, 2006(4): 327–332. |
| [13] | Rahman M, Zhu H, Yu A, et al. DEM simulation of particle percolation in a packed bed[J]. Particuology, 2008, 6(6): 475–482. DOI:10.1016/j.partic.2008.07.016 |
| [14] | Zhu H P, Rahman M, Yu A B, et al. Effect of particle properties on particle percolation behaviour in a packed bed[J]. Minerals Engineering, 2009, 22(11): 961–969. DOI:10.1016/j.mineng.2009.03.002 |
| [15] | Li J, Yu A B, Bridgwater J, et al. Spontaneous inter-particle percolation:A kinematic simulation study[J]. Powder Technology, 2010, 203(2): 397–403. DOI:10.1016/j.powtec.2010.05.037 |
| [16] | Zhu H P, Yu A B. The effects of wall and rolling resistance on the couple stress of granular materials in vertical flow[J]. Physical A:Statistical Mechanics and its Applications, 2003, 325(3): 347–360. |
 2015, Vol. 38
2015, Vol. 38


