钢帘线盘条是一种高端线材产品，是生产钢帘线的必备原材料，是发展现代汽车工业的重要原材料之一。钢帘线是以高强度极细钢丝按一定结构捻制成的钢丝束，主要用于生产汽车子午线轮胎。采用钢帘线作为骨架材料的汽车子午线轮胎具有使用寿命长、安全性能好、节能环保、耐穿刺、弹性好等特点，在发达国家的使用率已经很高。钢帘线也称钢丝帘线，其质量问题主要是钢中的脆性夹杂物经常导致盘条在拉拔成钢丝过程中断裂^[1]。因此，在出钢过程中采用无铝脱氧，在精炼过程中通过变渣工艺来降低钢液中酸溶铝含量和总氧含量，最终减少钢中的脆性夹杂物^[2-4]。精炼中的变渣工艺就是在精炼初期造白渣将碱度调至2.0左右，目的是充分脱氧与脱硫，达到目标值后加硅砂调渣，将碱度降至0.7~1.0；在碱度降低情况下，钢液不可避免地会产生回硫，同时，FeO对钢液回硫也有着一定的影响。FeO带入Fe²⁺和O^2-，但它们对脱硫反应有相反的作用，O^2-浓度增加，使硫在渣-钢中的分配系数(L_S)增加，但Fe²⁺浓度增加，则使L_S降低，因为渣中Fe²⁺的增多使钢液的w(O)增加，因此FeO活度低时，L_S才有较高的值。通过建立活度计算模型开展含FeO多元渣系的热力学研究，探究FeO活度的影响因素，为进一步分析和控制FeO对于回硫的影响提供理论指导。文中基于熔渣结构的分子离子共存理论^[5]，建立了SiO₂-Al₂O₃-CaO-MgO-FeO-MnO六元渣系的活度计算模型。

1 熔渣活度计算模型

共存理论模型最初由前苏联的丘依柯^[6]提出，后经张鉴^[5]修正，成为一套完整的模型体系。其主要内容是基于溶液中同时存在离子和分子的事实，建立离子、简单分子和复合分子之间的化学平衡关系。根据已有的化学平衡热力学数据计算组元的作用浓度，并以其表征组元活度。共存理论已在冶金炉渣中取得了良好的应用效果。文中根据熔渣结构的分子离子共存理论，建立了SiO₂-Al₂O₃-CaO-MgO-FeO-MnO六元渣系的活度计算模型。

1.1 结构单元

根据分子离子共存理论, 查阅CaO-Al₂O₃-SiO₂、CaO-MgO-SiO₂、MgO-Al₂O₃-SiO₂、CaO-SiO₂、MgO-SiO₂、Al₂O₃-MnO-FeO等相图^[7]，确定1 550~1 650 ℃时本渣系的结构单元如下：

简单离子：Ca²⁺、Fe²⁺、Mg²⁺、Mn²⁺、O^2-；

分子化合物：SiO₂, Al₂O₃，3CaO^·Al₂O₃, 12CaO·7Al₂O₃, CaO·Al₂O₃, CaO·2Al₂O₃, CaO·6Al₂O₃, CaO·SiO₂, 3CaO·2SiO₂, 2CaO·SiO₂, 3CaO·SiO₂, 3Al₂O₃·2SiO₂, 2MgO·SiO₂, MgO·SiO₂, MgO·Al₂O₃·2FeO·SiO₂, FeO·Al₂O₃, MnO·SiO₂, 2MnO·SiO₂, 2CaO·Al₂O₃·SiO₂, CaO·Al₂O₃·2SiO₂, 2CaO·MgO·2SiO₂, 3CaO·MgO·2SiO₂, CaO·MgO·iO₂, CaO·MgO·2SiO₂。

1.2 模型的建立

确定熔渣的结构单元后，依据共存理论可建立反应的平衡常数方程。

设：a=SiO₂, b=Al₂O₃, c=CaO, d=MgO, e=FeO, f=MnO，N₁=SiO₂，N₂=Al₂O₃，N₃=CaO，N₄=MgO，N₅=FeO，N₆=MnO，N₇=3CaO·Al₂O₃，N₈=12CaO·7Al₂O₃，N₉=CaO·Al₂O₃，N₁₀=CaO·2Al₂O₃，N₁₁=CaO·6Al₂O₃，N₁₂=CaO·SiO₂，N₁₃=3CaO·2SiO₂，N₁₄=2CaO·SiO₂，N₁₅=3CaO·SiO₂，N₁₆=3Al₂O₃·2SiO₂，N₁₇=2MgO·SiO₂，N₁₈=MgO·SiO₂，N₁₉=MgO·Al₂O₃，N₂₀=2FeO·SiO₂，N₂₁=FeO·Al₂O₃，N₂₂=MnO·SiO₂，N₂₃=2MnO·SiO₂，N₂₄=2CaO·Al₂O₃·SiO₂，N₂₅=CaO·Al₂O₃·2SiO₂，N₂₆=2CaO·MgO·2SiO₂，N₂₇=3CaO·MgO·2SiO₂，N₂₈=CaO·MgO·SiO₂，N₂₉=CaO·MgO·2SiO₂。

其中a, b, c, d, e, f为反应前SiO₂，Al₂O₃，CaO，MgO，FeO，MnO物质的量(设总物质的量为1)。N_i(i=1, 2，…，29)为平衡时熔渣中各组元的有效浓度，即定义为各组元的活度。

该模型所涉及的化学反应式、吉布斯自由能变、以及复杂分子有效浓度的表达式，如表 1所示^[8-12]。其中K_i(i=1, 2, …, 33)为各个反应的平衡常数，由ΔG求得。根据炉渣内各物质的质量平衡关系，可建立熔渣的活度计算模型如下式(1)-(6)。

$\begin{array}{l} {N_{\rm{1}}}{\rm{ + }}{N_{\rm{2}}}{\rm{ + }}{{\rm{N}}_{\rm{3}}}{\rm{ + }}{N_{\rm{4}}}{\rm{ + }}{N_{\rm{5}}}{\rm{ + }}{N_{\rm{6}}}{\rm{ + }}{N_{\rm{7}}}{\rm{ + }}{N_{\rm{8}}}{\rm{ + }}{N_{\rm{9}}}{\rm{ + }}{N_{{\rm{10}}}}{\rm{ + }}{N_{{\rm{11}}}}{\rm{ + }}{N_{{\rm{12}}}}{\rm{ + }}{N_{{\rm{13}}}}{\rm{ + }}{N_{{\rm{14}}}}{\rm{ + }}{N_{{\rm{15}}}}{\rm{ + }}{N_{{\rm{16}}}}{\rm{ + }}{N_{{\rm{17}}}}\\{\rm{ + }}{N_{{\rm{18}}}} {\rm{ + }}{N_{{\rm{19}}}}{\rm{ + }}{N_{{\rm{20}}}}{\rm{ + }}{N_{{\rm{21}}}}{\rm{ + }}{N_{{\rm{22}}}}{\rm{ + }}{N_{{\rm{23}}}}{\rm{ + }}{N_{{\rm{24}}}}{\rm{ + }}{N_{{\rm{25}}}}{\rm{ + }}{N_{{\rm{26}}}}{\rm{ + }}{N_{{\rm{27}}}}{\rm{ + }}{N_{{\rm{28}}}}{\rm{ + }}{N_{{\rm{29}}}}{\rm{ = 1, }} \end{array}$

(1)

$\begin{array}{l} b \times ({N_1} + {N_{12}} + 2 \times {N_{13}} + {N_{14}} + {N_{15}} + 2 \times {N_{16}} + {N_{17}} + {N_{18}} + {N_{20}} + {N_{22}} + {N_{23}} + {N_{24}}\\ + 2 \times {N_{25}} + 2 \times {N_{26}} + 2 \times {N_{27}} + {N_{28}} + 2 \times {N_{29}}) = a \times ({N_2} + {N_7} + 7 \times {N_8} + {N_9} + \\2 \times {N_{10}} + 6 \times {N_{11}} + 3 \times {N_{16}} + {N_{19}} + {N_{21}} + {N_{24}} + {N_{25}}), \end{array}$

(2)

$\begin{array}{l} c \times ({N_2} + {N_7} + 7 \times {N_8} + {N_9} + 2 \times {N_{10}} + 6 \times {N_{11}} + 3 \times {N_{16}} + {N_{19}} + {N_{21}} + {N_{24}} + {N_{25}}) \\= b \times ({N_3} + 3 \times {N_7}+ 12 \times {N_8} + {N_9} + {N_{10}} + {N_{11}} + {N_{12}} + 3 \times {N_{13}} + \\2 \times {N_{14}} + 3 \times {N_{15}} + 2 \times {N_{24}} + {N_{25}} + 2 \times {N_{26}} + 3 \times {N_{27}} + {N_{28}} + {N_{29}}), \end{array}$

(3)

$\begin{array}{l} d \times ({N_3} + 3 \times {N_7} + 12 \times {N_8} + {N_9} + {N_{10}} + {N_{11}} + {N_{12}} + 3 \times {N_{13}} + 2 \times {N_{14}} + 3 \times {N_{15}} +\\ 2 \times {N_{24}} + {N_{25}} + 2 \times {N_{26}} + 3 \times {N_{27}} + {N_{28}} + {N_{29}}) \\= c \times ({N_4} + 2 \times {N_{17}} + {N_{18}} + {N_{19}} + {N_{26}} + {N_{27}} + {N_{28}} + {N_{29}}), \end{array}$

(4)

$f \times ({N_4} + 2 \times {N_{17}} + {N_{18}} + {N_{19}} + {N_{26}} + {N_{27}} + {N_{28}} + {N_{29}}) = d \times ({N_6} + {N_{22}} + 2 \times {N_{23}}),$

(5)

$e \times ({N_6} + {N_{22}} + 2 \times {N_{23}}) = f \times ({N_5} + 2 \times {N_{20}} + {N_{21}})。$

(6)

式(1)-(6)及表 1中的质量作用浓度的表达式即为渣系SiO₂-Al₂O₃-CaO-MgO-FeO-MnO的活度计算模型。

使用商业软件Matlab对模型进行编程计算，计算过程采用迭代算法。将现场冶炼帘线钢的炉渣平均成分(如表 2所示)代入模型进行计算。

模型中温度分别设置为T=1 500、1 550、1 600 ℃，由此可计算出不同温度条件下六元渣系中各组元的活度值以及总的平均摩尔分数$\sum n$，如表 3所示。

由表 3可以看出，在炼钢温度下酸性精炼渣中SiO₂、FeO、MgO、MnO的活度较大，CaO次之，而Al₂O₃的活度较小。这主要是由于炉渣中Al₂O₃除少部分Al₂O₃的简单分子形式存在外，绝大部分与CaO、FeO等物质相结合形成复合分子，所以，其简单分子的活度较小。炉渣内CaO和FeO由于与多种酸性氧化物和两性氧化物反应生成了复合分子，从而使得熔渣中CaO、FeO的活度对其他组元活度产生了较大的影响。熔渣中FeO主要赋存物相为FeO·Al₂O₃，FeO的活度随着温度的上升而增加，而主要赋存物相FeO·Al₂O₃的活度随着温度的上升则有所减小。通过以上分析可以看出，表 2渣系在炼钢温度下，FeO主要以FeO·Al₂O₃的形式存在，其次是2FeO·SiO₂。因此，其活度受熔渣中Al₂O₃和SiO₂含量的影响较大。

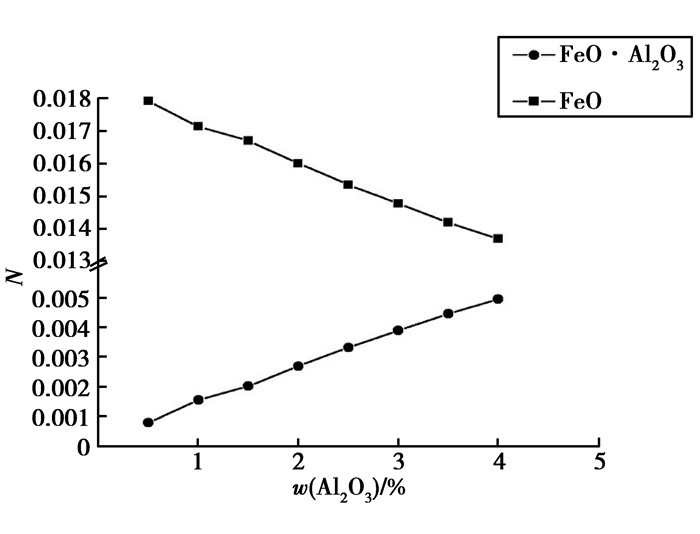
2 结果和讨论 2.1 熔渣中Al₂O₃含量对FeO相关组元活度的影响

在模型计算条件下，当碱度为1时、MgO质量分数为5%、MnO含量为0.5%和FeO质量分数为1%时，计算得到1 823 K时熔渣中与FeO相关组元的活度随w(Al₂O₃)的变化曲线如图 1所示。由图 1可知，炉渣中的FeO活度随着Al₂O₃质量分数的升高而降低，而FeO·Al₂O₃的活度增加。这是由于随着Al₂O₃质量分数的增加，一方面CaO的质量分数会减少，生成的硅钙化合物减少，SiO₂和FeO生成2FeO·SiO₂增加，导致FeO活度减少；另一方面增加的Al₂O₃也会与FeO开始反应生成FeO·Al₂O₃，并逐渐增多，导致FeO活度减少。因此，呈现出FeO的活度减小，而FeO·Al₂O₃的活度增加。

2.2 熔渣中FeO质量分数对FeO活度的影响

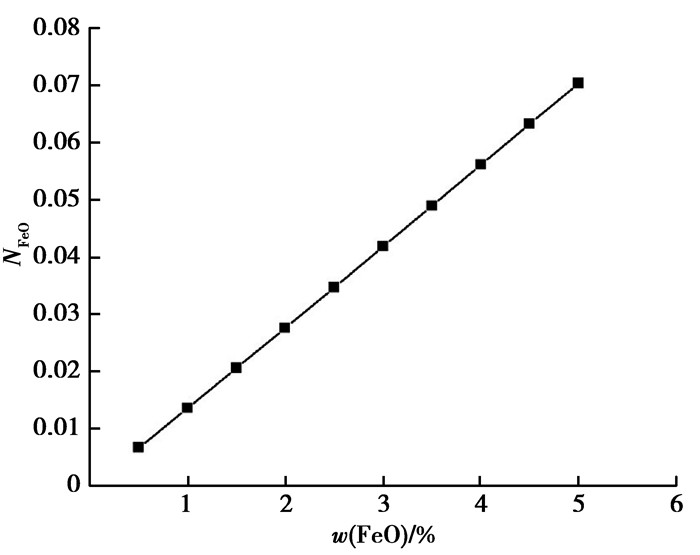
当SiO₂-Al₂O₃-CaO-MgO-FeO-MnO渣系二元碱度为1、Al₂O₃质量分数为4%、MgO质量分数为5%和MnO含量为0.5%时，计算得1 823 K时炉渣FeO活度受渣中FeO质量分数的影响如图 2所示。由图 2可知，随渣中FeO质量分数的增加，炉渣FeO活度增加，且近似呈线性增长趋势。这说明，在其他条件不变时，渣中FeO质量分数增加，渣中Fe²⁺和O^2-增多，即渣中自由FeO的浓度增大，从而使FeO活度增大，与此同时，可以看出FeO质量分数越大，对FeO活度影响越显著。

2.3 熔渣碱度对FeO活度的影响

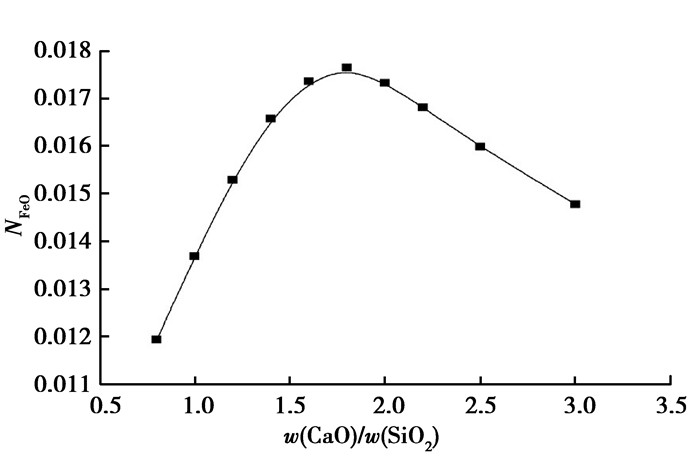
在本模型计算条件下，当Al₂O₃含量为4%、MgO含量为5%、MnO含量为0.5%和FeO含量为1%时，计算得到1 823 K时炉渣中FeO活度随炉渣二元碱度的变化见图 3。由图 3可知，随着二元碱度的增加，FeO活度呈现出先增加后减小的趋势。这是由于CaO比FeO有较强的碱性，因而它与SiO₂结合，致使熔渣中自由FeO增多，熔渣对理想溶液形成正偏差，γ_FeO=1。随着碱度的不断增加，带入的CaO不断与SiO₂形成复杂化合物，致使自由FeO量增多，FeO活度也就不断增加。当碱度达到1.8时，FeO活度达到很高的值。之后碱度再增加，FeO活度则有所下降，这是因为有铁酸钙复合化合物的形成，使自由FeO的含量下降，从而FeO活度的减小。从离子理论的观点^[13]，可认为FeO-SiO₂内有较为复杂的Si_xO_y^z-。当碱度提高，O^2-数增加时，一方面使Si_xO_y^z-解体，成为比较简单的结构；另一方面，与Fe²⁺形成强离子对Fe²⁺·O^2-, 而Ca²⁺则存在于解体后形成的比较简单的络离子周围，成为弱离子对，如Ca²⁺·Si₂O₇^6-等，因此FeO活度增加。当碱度达到1.8时，络离子以最简单的SiO₄^4-形式存在，这时进入的O^2-不再被消耗于络离子的解体，Fe²⁺·O^2-离子浓度达到最大值，而FeO活度也达到最大值。当碱度再提高时，熔渣中有近似铁酸钙组成的铁氧络离子FeO₂^-形成，因而Fe²⁺和O^2-浓度下降，从而FeO活度降低。

3 结论

1) 根据分子离子共存理论，建立了SiO₂-Al₂O₃-CaO-MgO-FeO-MnO渣系的活度计算模型，计算结果表明在炼钢温度下酸性精炼渣中SiO₂、FeO、MgO、MnO的活度较大，CaO次之，而Al₂O₃的活度较小；熔渣中FeO主要赋存物相为FeO·Al₂O₃，FeO的活度随着温度的上升而增加，而主要赋存物相FeO·Al₂O₃的活度随着温度的上升则有所减小。

2) 当碱度w(CaO)/w(SiO₂)=1、MgO含量为5%、MnO含量为0.5%和FeO含量为1%时，FeO的活度随着w(Al₂O₃)的增加而减小。

3) 当SiO₂-Al₂O₃-CaO-MgO-FeO-MnO渣系二元碱度为1、Al₂O₃含量为4%、MgO含量为5%和MnO含量为0.5%时，FeO的活度随着w(FeO)的增加呈线性增加。

4) 当Al₂O₃含量为4%、MgO含量为5%、MnO含量为0.5%和FeO含量为1%时，FeO的活度随着碱度的增加而先增加后减小，在碱度为1.8时，达到最大值。