2. 东北大学 材料与冶金学院,沈阳 110004
2. School of Materials and Metallurgy, Northeast University, Shenyang 11004, P.R.China
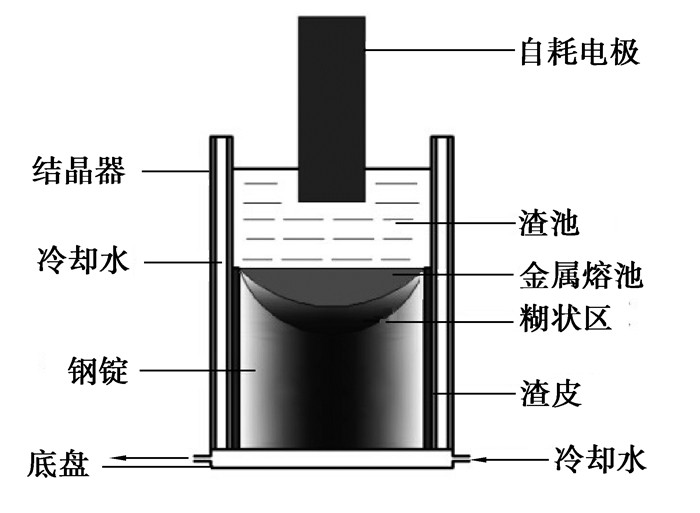
电渣重熔(Electroslag remelting)是将由一般方法生产出来的钢进行再精炼的特种冶金工艺,可以生产洁净钢和超合金钢,熔渣有助于去除钢中夹杂物和有害元素,而且,在渣池的保护作用下,可以避免钢锭再氧化,从而提高钢锭的质量。电渣重熔是将作为原料的自耗电极一端插入熔渣内,当电流流过电阻较高的渣池时,渣池内会产生大量的焦耳热将自耗电极熔化,熔融金属在外力的作用下汇聚成熔滴,发生滴落并穿过渣池,通过渣金界面形成金属熔池,在冷却水的作用下,逐渐凝固形成钢锭,电渣重熔过程示意图如图 1所示。
|
图 1 电渣重熔过程示意图 Figure 1 Schematic diagram of the Electroslag Remelting |
电渣重熔过程伴随着流体流动,传热和传质以及凝固熔化等复杂的物理现象,还涉及电磁场、流场和温度场之间的相互作用,通过实验的方法很难定量分析操作参数对重熔过程的影响;而通过数值模拟研究操作参数对重熔过程及钢锭质量的影响是一种科学而有效的方法[1]。
Choudhary等[2]采用二维轴对称模型,分析了工艺参数对金属熔池的形状、速度场和温度场的影响,但其模型并未考虑熔滴对过程的影响。Kelkar等[3-4]通过二维轴对称稳态数学模型模拟了不同熔化速率下的电渣重熔过程以及重熔过程的不同时期钢锭逐渐形成的行为变化。Li等[5-6]采用三维有限元模型对电渣重熔过程中的电磁场和温度场以及金属熔池的形状变化进行了研究分析。Jeff等[7]通过数值模拟的方法,预测了不同操作条件下的熔化速率和金属熔池形状变化,并与实验测量值做出了比较。Weber[8]建立了能够考虑电磁、流体流动、传热和相变现象的二维轴对称数学模型,主要是对金属熔池形状做出了比较。魏季和等[9]建立了电渣重熔过程渣池磁场和流场数学模型,但忽略了热浮力对渣池流动行为的影响。刘福斌等[10]采用ANSYS对电渣重熔过程渣池流场进行了数学模拟。刘艳贺等[11]通过ANSYS计算电磁场,以稳态形式加入FLUENT中作为计算的初始条件建立了三维数学模型,但加入稳态磁场相当于对实际过程做了简化处理,不能体现熔滴滴落过程中电流及电磁场的变化。王晓花等[12]通过数学模型分析了电渣重熔工艺(电极形貌、插入深度和电流强度)对渣池磁流体力学行为的影响规律,但其模型也不能考虑流动对电磁场的影响。总的来说,虽然有不少研究者都通过建立数学模型研究了工艺参数对重熔过程的影响,但其模型未能同时考虑电磁与流体的相互作用,或未能考虑重熔过程的三维性,笔者则希望通过已建立的三维耦合电磁流体的模型来研究工艺参数的影响。
在电渣重熔过程中,提高冶炼速度往往是通过增加电流来实现的,这会使得金属熔池的深度增加,影响结晶线的形状进而影响铸坯的质量。因此,熔化速率是关键操作参数,它对生产出的钢锭质量有着重要的影响,通过研究熔化速率对重熔过程的影响,比较并分析不同熔化速率下的各物理场变化情况及分布情况,进而优化工艺参数。
1 数学模型选取了3个不同的电压值,以此来控制其熔化速率的大小,具体的几何参数见表 1;渣和钢锭的物性参数以及过程参数如表 2和表 3所示。
| 表 1 几何参数 Table 1 Geometrical parameters |
| 表 2 渣和钢锭的物性参数 Table 2 Physical property of the metal and slag |
| 表 3 过程参数 Table 3 Process parameters |
1) 模型简化
为了简化计算过程,做出如下的假设:
a.忽略电极的运动,入口条件设为质量入口;
b.金属的热导率和熔渣的密度随着温度的变化而变化[1],其余物性参数均设为常数;
c.对于凝固过程,不考虑凝固收缩[5];
d.熔渣的粘度设为常数。
2) 控制方程
描述电渣重熔过程所用到的基本控制方程包括质量守恒方程、动量守恒方程和能量守恒方程以及Maxwell方程组
基本控制方程包括质量守恒方程、动量守恒方程和能量守恒方程以及Maxwell方程组。
| $ \nabla \bullet (\rho \boldsymbol{u}) = 0, $ | (1) |
| $ \frac{\partial }{{\partial t}}(\rho \boldsymbol{u}) + \nabla \bullet (\rho \boldsymbol{uu}) =-\nabla p + \mu {\rm{_{eff}}}{\nabla ^2}\boldsymbol{u} + \rho \boldsymbol{g} = {\boldsymbol{F}_{\rm{e}}}, $ | (2) |
| $ \frac{\partial }{{\partial t}}(\rho E) + \nabla \bullet \rho \boldsymbol{u}E = \nabla \bullet ({k_{{\rm{eff}}}}\nabla T) + {Q_{{\rm{Joule}}}}{\rm{。}} $ | (3) |
基于Maxwell方程组求解电磁场
| $ \nabla \times \boldsymbol{E} =-\frac{{\partial \boldsymbol{B}}}{{\partial t}}, $ | (4) |
| $ \nabla \bullet \boldsymbol{j} = 0, $ | (5) |
| $ \boldsymbol{E} =-\nabla \varphi-\frac{{\partial \boldsymbol{A}}}{{\partial t}}。 $ | (6) |
通过方程(4)和(6),可导出
| $ \boldsymbol{B} = \nabla \times \boldsymbol{A}, $ | (7) |
| $ {{\vec F}_{\rm{e}}} = \boldsymbol{j} \times \boldsymbol{B}, $ | (8) |
| $ {Q_{{\rm{Joule}}}} = \frac{1}{\sigma }\boldsymbol{j} \bullet \boldsymbol{j}, $ | (9) |
式中:ρ为密度;u为速度矢量;p为静压;μeff有效黏度系数;g为重力加速度;E为总能量;keff为导温系数;T为温度;E为电场强度向量;φ为标量势;A为矢量势;j为电流密度向量;B为磁感应强度向量;Fe为电磁力;QJoule为焦耳热;σ为电导率。
考虑到电渣重熔过程的流动特点,采用VOF模型对渣金界面进行追踪。对于钢锭的熔化凝固,使用FLUENT中的凝固熔化模型,为使两相界面更明晰,糊状区的参数设为107;凝固熔化问题采用焓-多孔介质的方法求解;采用电势法求解电磁场,通过用户自定义函数定义源项求解出电磁力,然后加载到动量方程中,焦耳热则作为源项加载到能量方程中。
3) 参数设置
电渣的密度采用Boussinesq模型描述,即只考虑温度变化引起的密度变化,且密度的变化并不显著改变流体的性质;金属的热导率通过Piecewise-Polynomial模型描述,即采用分段多项式的方式将液固相热导率区分开。
4) 边界条件
进出口的边界条件设定为质量入口和流量出口,出口处电势为零。壁面采用无滑移边界条件,渣池和空气的接触面采用零剪切应力边界条件,换热方式为对流和辐射换热。
所采用的数学模型已经由实验验证,所研究对象的详细参数可参见文献[13]。
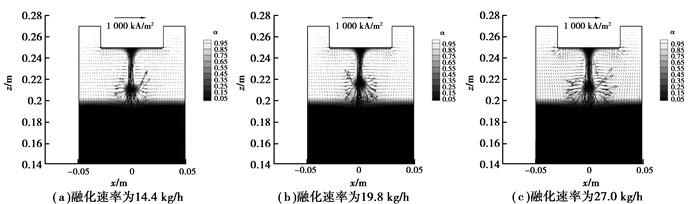
2 模拟结果与讨论 2.1 电磁场分析图 2是不同熔化速率下的电流密度分布情况,如图所示,电流密度随着熔化速率的增大而显著提高,在其他工艺参数都相同的情况下,熔化速率越高,入口的电流越大,相应的电流密度也会越大;同时,在电极逐渐熔化的过程中,电流集中于熔滴周围区域,这主要是由于金属的电导率相对较大,大部分电流都将从熔滴通过,因此,该区域的电流密度较大。
|
图 2 不同熔化速率下的电流密度分布 Figure 2 Current density distribution for different melting rate |
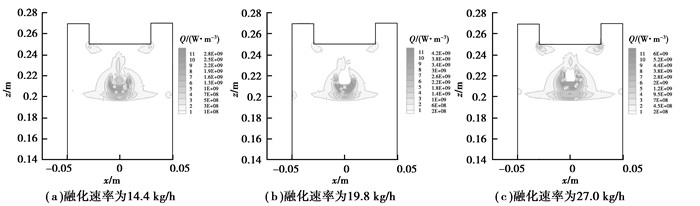
不同熔化速率下的焦耳热分布情况如图 3所示,焦耳热是熔化电极的热源,它与电流密度的变化趋势基本一致,也随熔化速率的增大而增大,与电流密度出现最大值的位置相同。
|
图 3 不同熔化速率下的焦耳热场分布 Figure 3 Joule heat distribution for different melting rate |
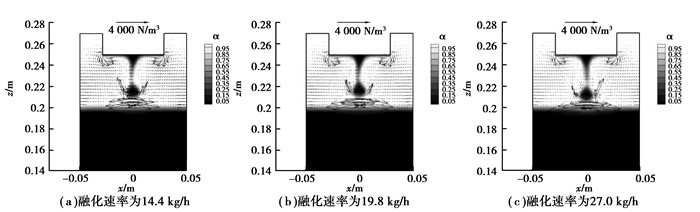
图 4是不同熔化速率下的电磁力分布情况,随着熔化速率的增大,电磁力变大;从图中可以看出,电磁力的方向与熔滴的运动方向相反,在熔滴形成过程中,随着熔滴质量的增大,作用在熔滴上的电磁力也越来越大,使其克服表面张力和重力的作用,产生颈缩效应,熔滴将发生滴落。
|
图 4 不同熔化速率下的电磁力分布 Figure 4 Electromagnetic force distribution for different melting rate |
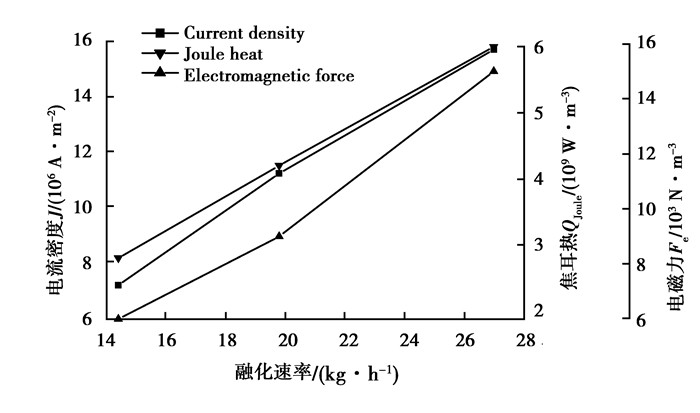
电流密度、焦耳热和电磁力均随着熔化速率的增大而增大,如图 5所示。当熔化速率为14.4 kg/h时,电流密度、焦耳热和电磁力的最大值依次是7.13×106 A/m2,2.8×109 W/m3,6×103 N/m3;当熔化速率为27.0 kg/h时,其最大值依次是1.57×107 A/m2,6×109 W/m3,1.5×104 N/m3;增大比例分别为120.20%,114.3%,150%;其根本原因在于电流的增大导致电流密度的增大,焦耳热和电磁力的分布与电流密度的分布直接相关。
|
图 5 不同熔化速率下的电流密度和焦耳热以及电磁力的变化 Figure 5 Variation of current density and joule heat and electromagnetic force for different melting rate |
为观察电渣重熔过程的温度和湍动能的变化情况,本文选取了距电极端头中心下方30 mm处为监测点,该点距渣金界面20 mm,属于渣池中心偏下的位置,能够反映出熔滴滴落过程的温度和湍动能的变化。
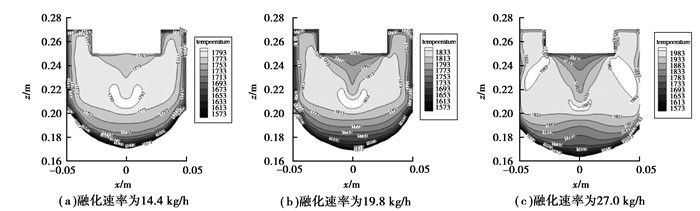
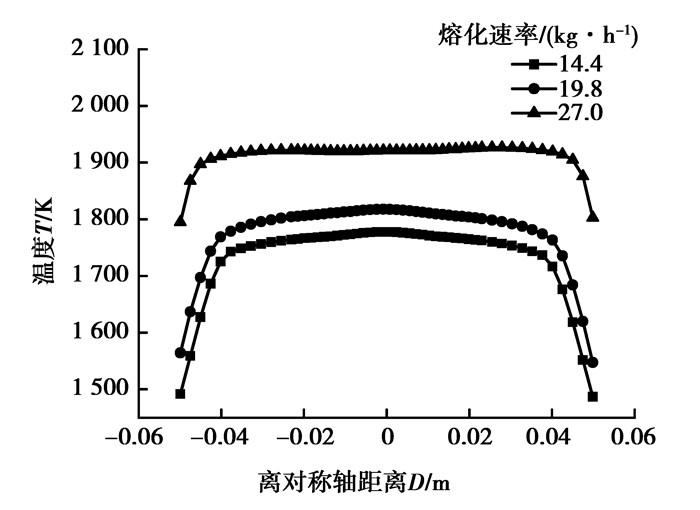
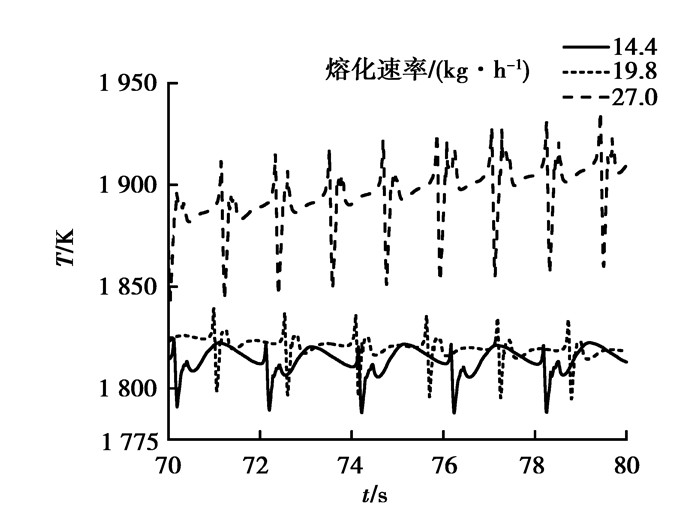
图 6给出了不同熔化速率下的温度分布情况,电渣重熔体系的温度值与熔化速率成正相关,这是因为熔化速率越大,其电流密度越大,而焦耳热是主要的热源,它的增大必然导致温度值变大,最大值分别为1 793,1 833,1 983 K,增大幅度分别为2.23%和8.18%。图 7是渣金界面处的温度比较,如图所示,渣金界面的温度也是呈增大趋势,渣金界面处的温度最大值分别是1 775,1 815,1 924 K,增大幅度分别为2.25%和6.01%。在熔滴滴落过程中,温度会发生波动,如图 8所示。在熔化速率大的情况下,监测点的温度相对较高,而且温度出现最大值的时间间隔变短,熔滴从渣池中带走的热量就会相对较多,经过渣金界面时,会使渣金界面的温度升高,通过渣金界面后,会将热量带入到金属熔池。
|
图 6 不同熔化速率下的温度分布 Figure 6 Temperature field distribution for different melting rate |
|
图 7 不同熔化速率下的渣金界面处温度比较 Figure 7 comparison of temperature of slag-metal interface for different melting rate |
|
图 8 不同熔化速率下的监测点的温度变化 Figure 8 Variation of the temperature at monitor point for different melting rate |
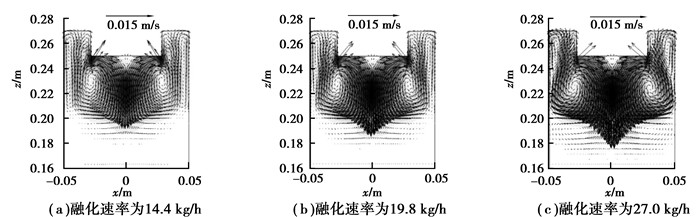
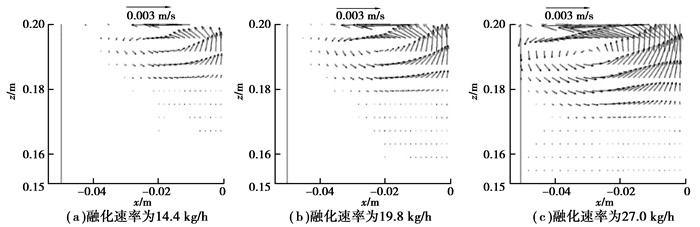
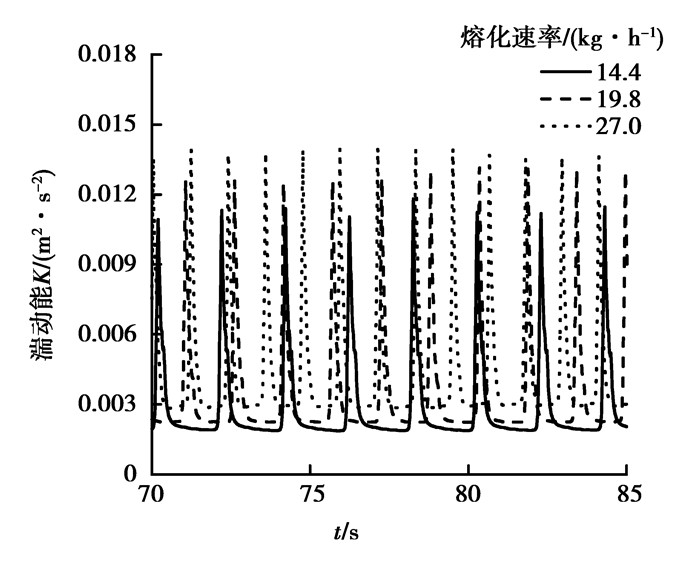
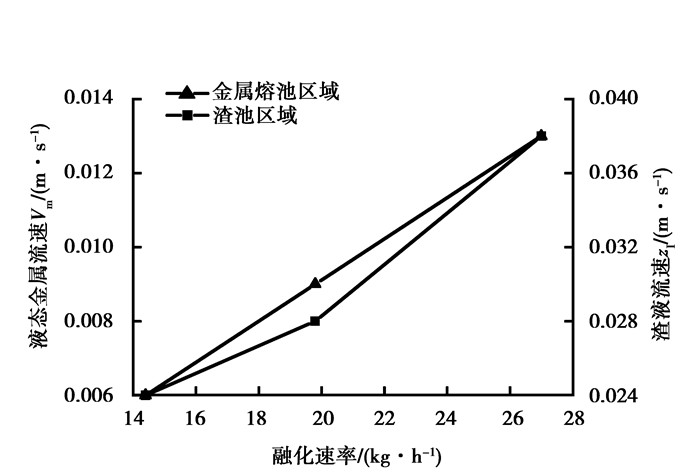
图 9和图 10分别为渣池区域和金属熔池区域的速度分布。电渣重熔体系的速度分布受电磁力、浮力、熔滴滴落以及冷却水的影响。渣池区域存在着两对涡,在电磁力和熔滴运动的作用下产生逆时针环流,位于渣池的中心位置;在浮力的作用下产生顺时针环流,位于结晶器侧壁附近。此外,随着熔化速率的增加,渣池中心的流动变得更强,速度值越来越大。监测点的湍动能变化如图 11所示,明显可以看到,受熔滴滴落的影响,监测点的湍动能呈现周期性振荡,但随着熔化速率的增大,湍动能的平均值在增大,振荡周期在变短。金属熔池区域的速度分布主要受浮力的影响,与渣池区域的速度值相比较小。图 12是2个区域速度最大值的变化曲线,渣池区域的速度最大值分别是0.024,0.028,0.038 m/s,增大幅度分别为16.7%和35.7%;金属熔池区域的速度场最大值分别是0.006,0.009,0.013 m/s,增大幅度分别为50%和44.4%。
|
图 9 不同熔化速率下的渣池区域速度场分布 Figure 9 Velocity field distribution of slag region for different melting rate |
|
图 10 不同熔化速率下的金属熔池区域速度场分布 Figure 10 Velocity field distribution of metal pool region for different melting rate |
|
图 11 不同熔化速率下的监测点的湍动能变化 Figure 11 Variation of the turbulent kinetic energy at monitor point for different melting rate |
|
图 12 不同熔化速率下的速度最大值比较 Figure 12 Comparison of maximum temperature for different melting rate |
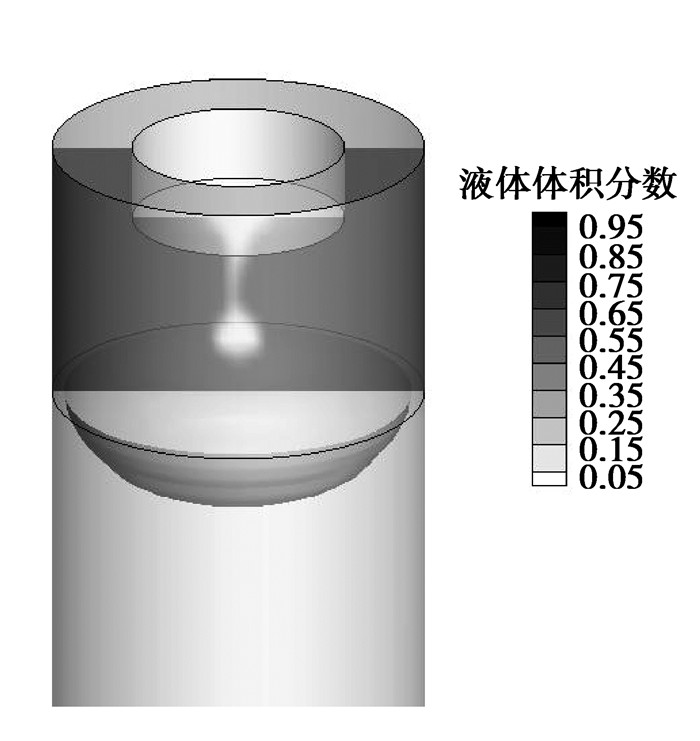
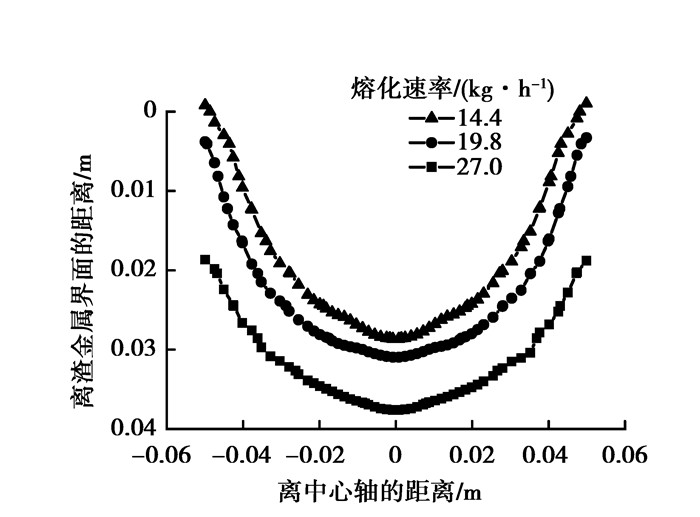
图 13给出了熔速为14.4 kg/h时金属熔池的三维形状。而图 14则对比了熔化速率对金属熔池形状的影响。随着熔化速率的增大,金属熔池更加浅平而且深度在增加,这是因为熔化速率的增大,等同于在相同的时间内,电极熔化的比例增加,金属熔池的容量势必会增大。熔滴作为热量的载体,进入金属熔池之后,会带入更多的热量,随着热量的不断增大,在相同的水冷条件下,结晶器内的冷却水并未能将热量及时带走,从图 6中的温度场分布情况可以看出,在大的熔化速率下,温度值相对较高,无论是在渣金界面以上区域还是以下区域,液态金属凝固将发生延迟现象,使金属熔池更加的浅平。另一方面,作为动量载体的熔滴,进入金属熔池之后,会产生扰动作用,从图 12中可以看出,渣池和金属熔池的速度值都随着熔化速率的增大而增大,熔滴携带的动能也会越大,这将使得熔池内的流动加强,促使熔池的深度增加。三种熔化速率下的金属熔池深度分别为27,31,38 mm。这三种熔化速率下,结晶前沿轮廓基本上呈现抛物面形状,由于柱状晶垂直于固液相界面生长,柱状晶方向与液面上升方向夹角小于45°,这对于铸坯的质量是很有利的。由于本文所研究的铸坯半径为28.5 mm,只有当熔速14.4 kg/h时,金属熔池的形状能够满足霍伊尔[14]提出的熔池深度等于或小于铸坯半径以及熔池上部圆柱形段高度小于10 mm的要求,这样才能更好地保证铸坯的凝固质量和表面光洁度。
|
图 13 金属熔池的形状 Figure 13 Metal melting pool shape |
|
图 14 不同熔化速率下的金属熔池形状比较 Figure 14 comparison of metal melting pool shape for the different melting rate |
为研究熔炼速度对电渣重熔过程的影响,本文建立了能够考虑电磁现象并耦合动量和热量传输的三维瞬态数学模型,对不同熔炼速度下的重熔过程做了的定量比较分析,得出如下结论:
1) 电流密度、焦耳热和电磁力都随着熔化速率的增大而增大,当熔化速率由14.4 kg/h增加到27.0 kg/h,各场值的增大比例分别为120.20%,114.3%,150%。
2) 随着熔化速率的增大,对温度最大值的影响远小于对速度最大值的影响;只有当熔速14.4 kg/h时,金属熔池的形状能够满足熔池深度等于或小于铸坯半径以及熔池上部圆柱形段高度小于10 mm的要求,以更好地保证铸坯的凝固质量和表面光洁度。
| [1] | Choudhary M, Szekely J. The modeling of pool profiles, temperature profiles and velocity fields in esr systems[J]. Metallurgical Transactions B, 1980, 11(3): 439–453. DOI:10.1007/BF02676888 |
| [2] | Choudhary M, Szekely J. The effect of temperature dependent electrical conductivity on flow and temperature fields in slags in esr systems[J]. Metallurgical Transactions B, 1981, 12(2): 418–421. DOI:10.1007/BF02654479 |
| [3] | Kelkar K M, Patankar S V, Mitchell A.Computational modeling of the electroslag remelting (esr) process used for the production of ingots of high-performance alloys[C]//Proceeding in International Symposium on Liquid metal Processing and Casting.USA, 2005:137-144. |
| [4] | Kelkar K M, Patankar S V, Srivatsa S K, et al.Computational modeling of electroslag remelting (esr) process used for the production of high-performance alloys[C]//Proceedings of the 2013 International Symposium on Liquid Metal Processing and Casting.USA, 2013:1-12. |
| [5] | Li B K, Wang F, Fumitaka T. Current magnetic field and joule heating in electroslag remelting processes[J]. The Iron and Steel Institute of Japan International, 2012, 52(7): 1289–1295. DOI:10.2355/isijinternational.52.1289 |
| [6] | Li B K, Wang B, Fumitaka T. Modeling of electromagnetic field and liquid metal pool shape in an electroslag remelting process with two series-connected electrodes[J]. Metallurgical and Materials Transactions B, 2014, 45(3): 1122–1132. DOI:10.1007/s11663-013-9996-4 |
| [7] | Jeff Y, Kyle F, Mike F, et al.Predictinig melting behavior of an industrial electroslag remelting ingot[C]//Proceedings of the 2013 International Symposium on Liquid Metal Processing and Casting.USA, 2013:47-55. |
| [8] | Weber V, Jardy A, Dussoubs B, et al. A comprehensive model of the electroslag remelting process:Description and Validation[J]. Metallurgical and Materials Transactions B, 2009, 40(3): 271–280. DOI:10.1007/s11663-008-9208-9 |
| [9] |
魏季和, 任永莉.
电渣重熔体系内熔渣流场的数学模拟[J]. 金属学报, 1994, 30(11): 481–490.
WEI Jihe, REN Yongli. Mathematical modelling of slag flow field in ESR systme[J]. Acta Metallurgica Sinica, 1994, 30(11): 481–490. (in Chinese) |
| [10] |
刘福斌, 姜周华, 藏喜民, 等.
电渣重熔过程渣池流场的数学模拟[J]. 东北大学学报(自然科学版), 2009, 30(7): 1013–1017.
LIU Fubin, JIANG Zhouhua, ZANG Ximin, et al. Mathematical modeling of flow field in slag bath during elecroslag remelting[J]. Jounal of Northeastern University (Natural Science), 2009, 30(7): 1013–1017. (in Chinese) |
| [11] |
刘艳贺, 贺铸, 刘双, 等.
电渣重熔过程电磁, 流动和温度场的数值模拟[J]. 过程工程学报, 2014, 14(1): 16–22.
LIU Yanhe, HE Zhu, LIU Shuang., et al. Numerical simulation of electromagnetic, flow and temperature fields in electroslag remelting process[J]. The Chinese Journal of Process Engineering, 2014, 14(1): 16–22. (in Chinese) |
| [12] |
王晓花, 厉英.
电渣重熔过程渣池磁流体力学行为数值模拟[J]. 东北大学学报(自然科学版), 2014, 35(11): 1561–1564.
WANG Xiaohua, LI Ying. Numerical simulation of magnetohydrodynamic behavior of ESR slag[J]. Jounal of Northeastern University (Natural Science),, 2014, 35(11): 1561–1564. (in Chinese) |
| [13] |
刘双, 贺铸, 王强, 等.
电渣重熔过程中熔滴形成与滴落过程的数值模拟[J]. 过程工程学报, 2014, 14(5): 86–93.
LIU Shuang, HE Zhu, WANG Qiang, et al. Numerical simulation of the formation and dripping of the melt droplet in the electroslag remelting process[J]. The Chinese Journal of Process Engineering, 2014, 14(5): 86–93. (in Chinese) |
| [14] | Hoyle G. Electroslag processes:principles and practice[J]. Applied Science Sole Distributor in the Usa & Canada Elsevier Science, 1983: 62–63. |
 2015, Vol. 38
2015, Vol. 38

