结晶器是连铸机非常重要的组成部分,结晶器冷却水将钢液的绝大部分热量带出,使钢液形成一定厚度的凝固壳[1]。坯壳厚度太薄或者不均匀容易引起裂纹甚至导致漏钢等严重事故[2],因此掌握凝固壳厚度分布情况非常有必要。
测量结晶器内坯壳厚度除利用漏钢坯壳外,研究者较常采用的还有添加同位素和添加硫等方法[3]。然而同位素带有放射性,危害人体健康,并且成本高昂,现已普遍不再使用。数值模拟不受实验环境、实验材料和实验仪器等限制,能模拟真实的连铸环境条件,可以对多种复杂工况下的连铸过程进行模拟仿真[4],已经在结晶器凝固壳厚度监测上得到广泛运用。
蔡兆镇[5-6]等采用顺序耦合法,建立了描述板坯连铸结晶器内,钢液凝固过程过热行为的二维瞬态二维瞬态热/力耦合有限元分析模型。基于此模型对某高强船板钢凝固过程的热行为进行计算。
然而由于二维模型控制方程中不包括对流项,液穴中存在的对流传热效应通过人为增大导热系数的方法计算,并将各处的导热系数取为同一常数,所以对结晶器内流场和温度场计算精度较差[7]。而三维模拟方法可以同时考虑钢液的流动传热和凝固行为,是目前研究结晶器凝固过程的主流方法。
于海岐等[8]研究表明钢液的大部分耗热发生在结晶器窄面的钢液冲击点附近,但并未深入研究钢液冲击对坯壳厚度的影响。杨静波等[9]研究表明结晶器表面的流速受多种因素的影响,包括侵入式水口的形状、水口浸入深度等。因此笔者重点考虑钢液流场对坯壳厚度的影响。
虽然关于结晶器凝固壳的三维数值模拟研究较多[10-11],但一般研究均取结晶器宽面中心和窄面中心两个特征点进行讨论,还未见结晶器三维凝固壳的详细分析。此外,关于二维切片法与考虑流动的三维模拟计算的凝固壳的差异,也未见相关报道。
笔者针对断面1 780 mm×225 mm的板坯,考虑钢液流场与温度场的相互作用,利用FLUENT软件模拟结晶器内流场、温度场,计算整个结晶器内的三维凝固壳分布特征,从而对比不同水口下结晶器凝固形貌,并与二维切片法的凝固壳分布进行对比。
1 数学模型的建立结晶器内钢液涉及到流动、传热(包括凝固)等现象,实际情况极为复杂。为了能够便于计算,有必要在数值模拟中进行一定的假设和简化。
1.1 模型假设及简化本文对于钢液在结晶器内冷却凝固过程作了以下假设和简化[12]:
1) 认为结晶器内部流场和温度场对称,因此仅计算整个结晶器的1/4;
2) 忽略结晶器液面的传热;
3) 忽略结晶器振动对于流场和温度场的影响;
4) 钢液进行的流动为不可压缩的牛顿流体的稳态流动;
5) 结晶器内钢液按匀相介质处理;
6) 由于钢的相变潜热远小于凝固潜热,故忽略固态相变过程的影响。
1.2 主要方程结晶器内钢液的流动行为综合了流动、传热以及凝固现象。因此涉及到的方程有质量守恒方程、凝固方程、能量守恒方程、动量守恒方程以及标准k-ε双方程[13-14]。
1) 质量守恒方程。
任何流体的流动都必须满足质量守恒定律。据此,可以得到钢液稳态流动的质量守恒微分方程为
| $ \nabla \cdot \left( {\rho \boldsymbol{v}} \right) = {S_{{\rm{mass}}}}, $ | (1) |
式中:ρ为流体密度;v为流体速度;Smass为源项。
2) 凝固方程。
FLUENT软件以焓多孔介质模型来处理凝固过程。钢液中的热量用焓H包含了显热h和潜热ΔH,采用热焓法处理钢液的潜热[15],即
| $ H = h + \Delta H, $ | (2) |
| $ h = {h_{{\rm{ref}}}} + \int_{{T_{{\rm{ref}}}}}^T {{c_p}{\rm{d}}T}, $ | (3) |
式中:H为钢液的焓;ΔH为钢液潜热;h为钢液显热;href为参考焓;Tref为参考温度;cp为定压比热容。
3) 能量守恒方程。
能量守恒方程是含有热交换的流动体系都必须满足的基本方程。可表示为
| $ \nabla \cdot \left( {\rho \boldsymbol{v}H} \right) = \nabla \cdot \left( {{K_{{\rm{eff}}}}\nabla T} \right) + {S_{\rm{E}}}, $ | (4) |
式中:Keff为钢液的导热系数;SE为流体内热源及由于粘性力作用下机械能转换为热能的部分。
4) 动量守恒方程。
动量守恒定律也是任何流动体系都必须满足的定律。可表述为微元体中流体动量对时间的变化率等于外界作用在该微元体上的各种力之和,表达式为
| $ \nabla \cdot \left( {\rho \boldsymbol{vv}} \right) =-\nabla p + \nabla \overline{\overline \tau } + \rho \boldsymbol{g} + \boldsymbol{F}, $ | (5) |
式中:p为压强,
5) 标准k-ε双方程。
紊流是自然界的普遍流动状态,其速度和压力等物理量在空间和时间上均具有随机性质的脉动性。直接求解动量方程对计算要求极高,目前工程中还无法采用这种方法。对瞬态的动量守恒方程做时间平均处理,另外补充了反应湍流特性的湍动能方程k和湍动能耗散率方程,便形成了双方程模型[16]。
| $ \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{{\partial \left[{\left( {\mu + {\mu _t}/{\sigma _k}} \right)\left( {\partial k/\partial {x_j}} \right)} \right]}}{{\partial {x_j}}} + {G_k} + {G_b} -\rho \varepsilon -{Y_M} + {S_k}, $ | (6) |
| $ \frac{{\partial \left( {\rho {u_i}\varepsilon } \right)}}{{\partial {x_i}}} = \frac{{\partial \left[{\left( {\mu + {\mu _t}/{\sigma _\varepsilon }} \right)\left( {\partial \varepsilon /\partial {x_j}} \right)} \right]}}{{\partial {x_j}}} + {G_1}\varepsilon \left( {{G_k} + {C_3}{G_b}} \right)/k -{G_2}\rho {\varepsilon ^2}/k + {S_\varepsilon }, $ | (7) |
式中:ui为在i点的动力粘性系数;YM为可压缩湍流中脉动扩张的贡献,对于不可压缩流体他们的值为0;C1、C2、σk和σε均为常数,取值为C1=1.44,C2=1.92,σk=1.0,σε=1.3;Gk为由于平均速度梯度引起的湍动能产生项;Gb为由于浮力引起的湍动能生产项;Sk和Sε为源项。
1.3 边界条件1) 入口边界条件。
入口定义在浸入式水口的入口处,设置为速度进口(velocity-inlet)边界条件。入口的速度根据连铸机的拉速和质量守恒共同决定,同时假定入口截面上的速度分布是相同的。入口湍动能k和湍动能耗散率ε均为1×10-5[17]。
2) 出口边界条件。
出口定义在结晶器计算区域的底部,出口边界定义为出流(outflow)。适用于出口处的流动是完全发展的情况,即出口处与入口处质量守恒。
3) 壁面边界条件。
结晶器宽面和窄面静止且无滑移,热边界条件选择对流传热边界条件模型(Convection),并设置自由温度为300 K,传热系数的计算式[3]为
| $ $ | (8) |
式中z为距弯月面距离。
4) 结晶器自由液面和对称面。
结晶器自由液面和水口内壁设定为壁面,垂直于壁面的速度分量为零。由于结晶器内钢液的流动行为具有对称性,分别在宽面和窄面中心设定两个对称面,并且设定各物理量在对称面上的梯度为零。
1.4 物性参数本文中的网格采取疏密的全六面体网格,即在窄面表面20 mm以内网格宽度为2 mm,其他区域网格宽度为10 mm。根据参考文献[18],整理钢的物性参数见表 1。此外,使用的板坯结晶器尺寸及相关工艺参数如表 2所示。
| 表 1 钢的物性参数 Table 1 The physical properties of steel |
| 表 2 结晶器尺寸及相关工艺参数 Table 2 The technological parameter of casting |
基于表 1和表 2所列的条件,计算了4种条件下(凹底水口、平底水口、凸底水口以及无水口条件)结晶器内钢液的流场和温度场。
2 结果与讨论对不同水口的流场和温度场进行计算,可以得到凹底水口、平底水口、凸底水口以及无水口条件下,在宽面和窄面上的凝固壳厚度三维分布特征。并选取了3个不同的高度位置,结合钢液的流场对凝固壳的厚度分布进行分析。文中高度均以拉坯方向为正方向;宽面和窄面均以角部为原点,分别以指向宽面中心和窄面中心为正方向。
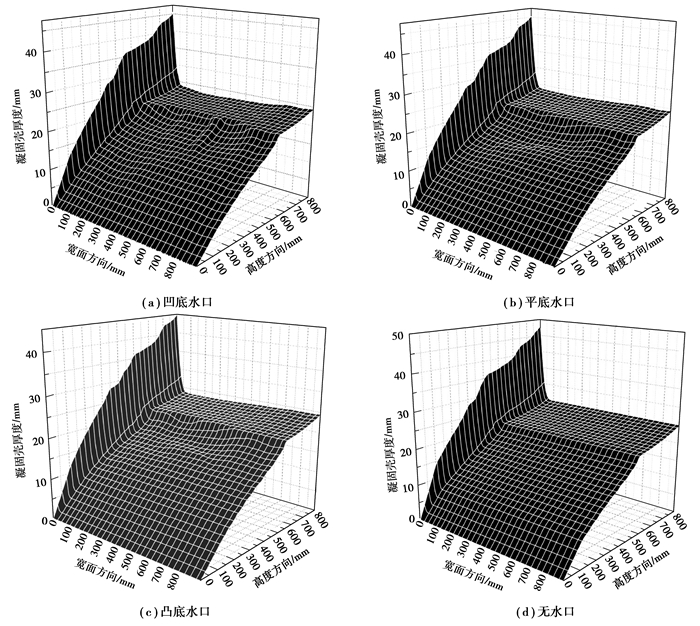
2.1 结晶器内三维凝固壳分布特征图 1和图 2分别表示在不同水口条件下,宽面和窄面凝固壳厚度分布的情况。从图中可以得到,在同一高度下角部是凝固壳厚度最大的位置;从结晶器上部至结晶器出口处,凝固壳凝固整体呈上升的趋势。但在结晶器下部区域出现了一个明显的平台,这是由于近壁面20 mm区域网格为2 mm,其他位置网格为10 mm造成的。
|
图 1 不同水口条件下的凝固壳宽面厚度的分布 Figure 1 The distribution of shell thickness in the wideside under different nozzles |
|
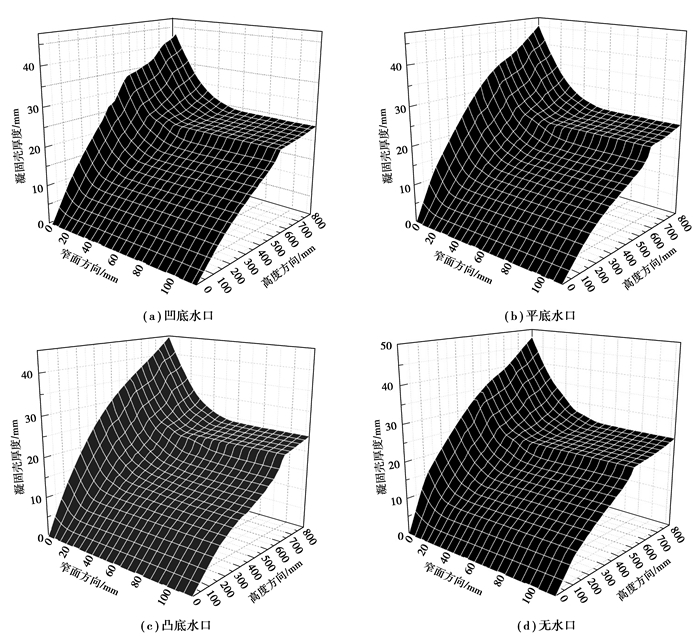
图 2 不同水口条件下的凝固壳窄面厚度的分布 Figure 2 The distribution of shell thickness in the narrowside under different nozzles |
在三维图中可以得出,凝固壳厚度在结晶器出口的角部位置达到最大。在有水口的条件下(包括凹型水口、平型水口和凸型水口)凝固壳厚度最大值约为45 mm;无水口条件下达到约47 mm。从宽面三维图中可以看到,有水口的条件下,在距离角部300 mm,顶部400 mm的区域,凝固壳分布曲面上都存在约2.5 mm的塌陷,而无水口条件下则没有。这是由于钢液出水口后流股逐渐扩散,流动对宽面该区域凝固壳的冲刷作用造成的。这种凹陷可能对铸坯的质量产生一定的影响。
而窄面之所以这种局部塌陷不明显,是因为窄面距离水口较远,流股扩散后覆盖了整个窄面,使得凝固坯壳不会受到强烈冲刷。
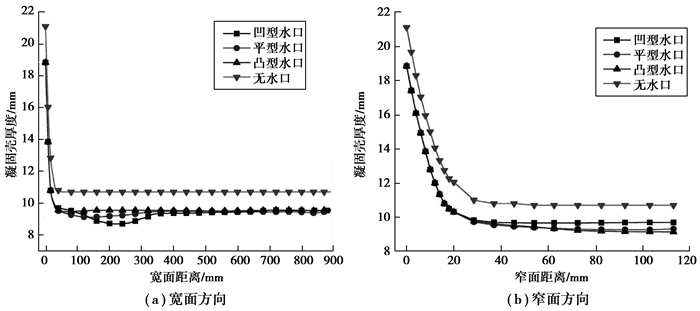
2.2 3个特征高度下的凝固壳厚度图 3、图 4和图 5分别是高度在200、500和800 mm,4种水口条件下结晶器横截面凝固壳的分布对比图。
|
图 3 高度为200 mm的横截面处凝固壳厚度分布 Figure 3 The shell thickness distribution of 200 mm below meniscus |
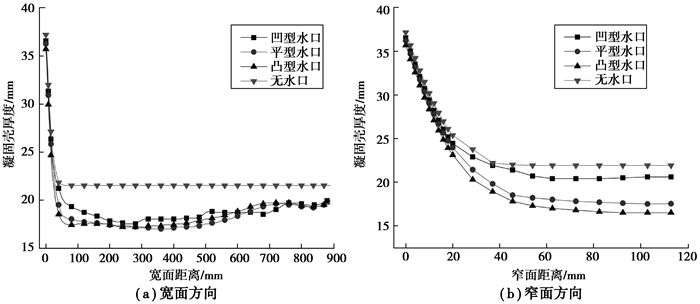
|
图 4 高度为500 mm的横截面处凝固壳厚度分布 Figure 4 The shell thickness distribution of 500 mm below meniscus |
|
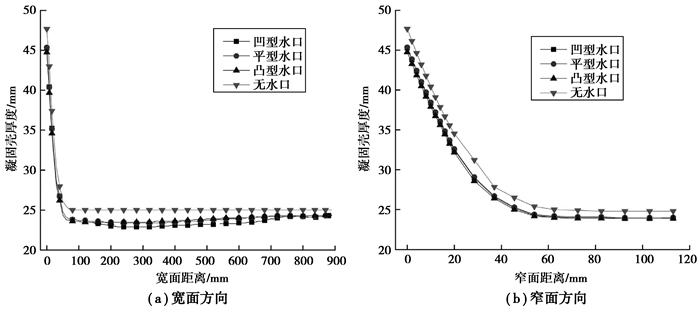
图 5 高度为800 mm的横截面处凝固壳分布 Figure 5 The shell thickness distribution of 800 mm below meniscus |
从3个高度的凝固壳厚度分布对比图可以看到:无水口条件下,凝固壳厚度明显大于有水口条件。这说明钢液冲刷对凝固壳厚度有明显的作用。
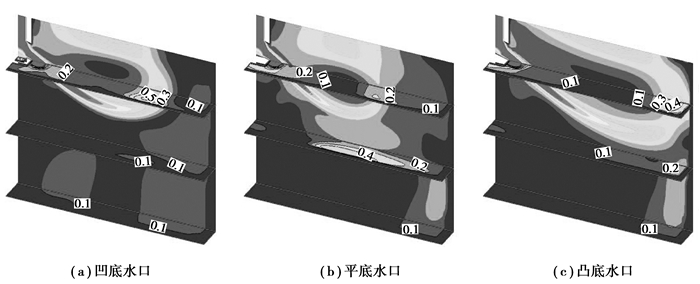
为了进一步考察钢液流动对凝固壳生长的影响,笔者详细比较了3种水口的流场对比图(图 6)。一个纵向的剖面为结晶器宽面对称面,3条横向的剖面分别对应于高度为200、500和800 mm。从流场图中可以得到,在凹型水口下,流股撞击水口底部,损失了很大一部分能量,导致出口流股的动能减小;在其他条件相同的情况下,使用平底水口时结晶器液面的活跃度比凹底水口强。对凸型水口,水口内的流股出水口时损失的能量很小,所以液面活跃度最大。
|
图 6 3种水口条件下的流场图 Figure 6 The flow flied graph in 3 different nozzles |
1) 高度为200 mm处凝固壳的厚度分布。
从图 3(a)上看,凹型水口在距离宽面200 mm区域的凝固壳比其他两种水口更薄,约1 mm。分析图 6在高度为200 mm处的流场可知,凹型水口在200~300 mm处流场强度比另外两种水口明显强一些,导致比另外两种水口的厚度要薄。
从窄面的流场看,显然凸型水口在窄面上的流场最强,平型次之,凹型水口在窄面的流场最弱。这与窄面凝固壳厚度出现的无水口最厚,其次凹型水口,再次平型水口,最薄是凸型水口非常吻合。因此说明所采用的流场冲刷影响凝固壳厚度是很明显的。但是由于钢液的扩散,对整个窄面都存在一定的冲刷,只是对窄面中心区域更强,因此窄面中心的凹陷仅有0.6 mm。
2) 高度为500 mm处凝固壳的厚度分布。
从图 4(a)中可以得到,在有水口的情况下,宽面中心的凝固壳厚度最大,而在宽面和角部之间有一个明显的减小(约2.5 mm),这就是图 1宽面的凹陷。这3种水口中,凹底的凝固壳厚度相对较大,而图 3中凹底还是最小的,这说明铸坯从200 mm运动到500 mm的过程中,凹底水口时,该区域的凝固壳受到冲刷较小,因而生长速度较快;而从流场图可以看出,平底水口在500 mm处的钢液流速很大,凸底水口在200~500 mm区间存在一个明显的高速冲刷区。
从流场的窄面上看,显然凸型水口在窄面上的流场最强,平型次之,凹型水口在窄面的流场最弱。这与窄面凝固壳厚度出现的无水口最厚,其次凹型水口,再次平型水口,最薄是凸型水口非常吻合。并且冲刷造成凝固壳厚度差异约2.5 mm。
3) 高度为800 mm处凝固壳厚度分布。
从宽面上看,在500 mm处3种水口下凝固壳的生长比较接近,从500~800 mm这段区域流场强度已经明显减弱,仅凹底水口的流场比其他两种水口略强,因此最终3种水口的凝固壳厚度相差甚微,凹底水口所对应的凝固壳厚度略低于其他两种水口。对于每一种水口,宽面中心并非凝固壳最薄的位置,是因为宽面中心虽然在水口处流场很强,但在后面的区域其流场弱于其他位置,受到的冲刷积累并不多。
从窄面上看,不同水口凝固壳厚度相差不大,约25 mm。主要原因是本文的网格采取的是疏密网格,在窄面表面有厚度为25 mm的区域为细网格,在粗细网格相交的地方部分数据有跳跃变化,产生较大的误差。
3 结论1) 无水口计算出的凝固壳厚度大于有水口的,并且结晶器凝固壳厚度从上到下逐渐增加,从角部到宽面和窄面中心减小,在角部位置为最大。在有水口的条件下(包括凹型水口、平型水口和凸型水口),角部位置凝固壳厚度最大值为约45 mm,宽面中心和窄面中心的凝固壳厚度为24 mm,无水口条件下凝固壳厚1~2 mm。
2) 钢液冲击凝固壳速度越大,对应位置的凝固壳越薄。钢液在结晶器高度为200~500 mm区域的冲刷最大;钢液流动和扩散会对在距离结晶器角部300 mm和顶部400 mm的宽面区域形成约2.5 mm的明显凹陷;同时钢液会冲刷结晶器整个窄面的凝固壳,以窄面中心最严重。
| [1] | Janik M, Dyja H, Janik M, et al. Modelling of three-dimensional temperature field inside the mould during continuous casting of steel[J]. Journal of Materials Processing Technology, 2004, 157(51): 177–182. |
| [2] |
刘青, 张建峰, 张晓峰, 等.
合金弹簧钢连铸坯高温力学性能分析[J]. 重庆大学学报, 2013, 36(3): 44–50.
LIU Qing, ZHANG Jianfeng, ZHANG Xiaofeng, et al. Analysis on high temperature mechanical properties of alloy spring steel billet[J]. Journal of Chongqing University, 2013, 36(3): 44–50. (in Chinese) |
| [3] |
蔡开科. 浇注与凝固[M]. 北京: 冶金工业出版社, 1987.
CAI Kaike. Pouring and solidification[M]. Beijing: Metallurgical Industry Press, 1987. (in Chinese) |
| [4] |
刘增勋.
方坯结晶器内气隙分布的数值分析[J]. 中国冶金, 2012, 22(5): 13–17.
Liu Zengxun. Numerical analysis on air-gap distribution in billet mould[J]. China Metallurgy, 2012, 22(5): 13–17. (in Chinese) |
| [5] | Cai Z. Simulation of thermal behavior during steel solidification in slab continuous casting mold i. mathematical model[J]. Acta Metallurgica Sinica, 2011, 47(6): 671–677. |
| [6] | Cai Z. Simulation of thermal behavior during steel solidification in slab continuous casting mold Ⅱ. model verification and results analysis[J]. Acta Metallurgica Sinica, 2011, 47(6): 678–687. |
| [7] | Mazumdar D. A Consideration about the concept of effective thermal conductivity in continuous casting[J]. The Iron and Steel Institute of Japan International, 1989, 29(6): 524–528. DOI:10.2355/isijinternational.29.524 |
| [8] |
于海岐, 朱苗勇.
板坯连铸结晶器内钢液过热消除过程的数值模拟[J]. 金属学报, 2009, 45(4): 476–484.
YU Haiqi, ZHU Miaoyong. Numerical simulation of liquid steel superheat removal in slab continous casting mold[J]. Acta Meatallurgica Sinaca, 2009, 45(4): 476–484. (in Chinese) |
| [9] |
杨静波, 李京社, 张江山.
板坯连铸结晶器内钢液流动的数值模拟[J]. 北京科技大学, 2014(36): 98–103.
YANG Jingbo, LI Jingshe, ZHANG Jiangshan. Simulation on fluid flow in a slab continous casting mould[J]. Journal of University of Science and Technology Beijing, 2014(36): 98–103. (in Chinese) |
| [10] | Vakhrushev A, Wu M, Ludwig A, et al. Numerical investigation of shell formation in thin slab casting of funnel-type mold[J]. Metallurgical & Materials Transactions B, 2014, 45(3): 1024–1037. |
| [11] | ZHANG De, SONG Lei, SHAN Zeng, et al. Thermo-mechanical modeling in continuous slab casting mould and its application[J]. The Iron and Steel Institute of Japan International, 2014, 54(2): 336–341. DOI:10.2355/isijinternational.54.336 |
| [12] |
钟宏.板坯连铸结晶器内凝固壳形成及厚度分布的数值模拟[D].重庆:重庆大学, 2010. ZHONG Hong.Slab continuous casting crystallizer in numerical simulation of solidification shell formation and thickness distribution[D]. Chongqing: Chongqing University, 2010.(in Chinese) |
| [13] | Shen J L, Chen D F, Xie X, et al. Influences of SEN structures on flow characters, temperature field and shell distribution in 420 mm continuous casting mould[J]. Ironmaking & Steelmaking, 2013, 40(4): 263–275. |
| [14] |
王成善, 李丹丹, 时艳文, 等.
扩散方程的稳态近似分析:Ⅰ.稳态近似法处理过程[J]. 重庆大学学报, 2014, 37(5): 53–63.
WANG Chengshan, LI Dandan, SHI Yanwen, et al. Analysis of diffusion equation based on steady state assumption Ⅰ. The process of steady state approximation[J]. Journal of Chongqing University, 2014, 37(5): 53–63. (in Chinese) |
| [15] |
杨权, 张真. 金属凝固与铸造过程数值模拟[M]. 杭州: 浙江大学出版社, 1996.
YANG Quan, ZHANG Zhen. Numerical simulation of metal solidification and casting process[M]. Hangzhou: Zhejiang University Press, 1996. (in Chinese) |
| [16] |
张兆顺, 崔桂香. 流体力学[M]. 北京: 清华大学出版社, 2006.
ZHANG Zhaoshun, CUI Guixiang. Fluid mechanics[M]. Beijing: Tsinghua University Press, 2006. (in Chinese) |
| [17] | Chaudhary R, Lee G G, Thomas B G, et al. Transient mold fluid flow with well-and mountain-bottom nozzles in continuous casting of steel[J]. Metallurgical & Materials Transactions B, 2008, 39(6): 870–884. |
| [18] | Meng Y, Thomas B G. Heat-transfer and solidification model of continuous slab casting: CON1D[J]. Metallurgical & Materials Transactions B, 2003, 34(5): 685–705. |
 2015, Vol. 38
2015, Vol. 38

