2. 中冶长天国际工程有限责任公司,长沙 410007
2. Zhongye Changtian International Engineering Co., Ltd., Changsha 410007, P.R.China
随着浅地表资源的不断开发利用,深凹露天矿的开采成为世界露天矿山开采发展的趋势,如美国的Bingham Canyon copper mine形成的深凹露天坑宽4.0 km,深1.2 km,边坡高达1.2 km。在深凹开采过程中随着开采深度的不断增加,边坡的安全性和稳定性越来越差。然而,对于深凹露天矿来说提高边坡角又是充分回收资源、降低开采成本和提高经济效益的重要手段。据相关研究,大型深凹露天矿边坡角提高一度,可节省剥岩费用数以千万乃至亿元。因此,深入开展深凹露天矿山边坡稳定性研究,对防治高边坡引起的地质灾害、提高矿山经济效益有着重要的理论与现实意义[1-4]。
边坡稳定性分析方法包括:工程地质分析法、极限平衡分析法、数值分析法等。传统的分析方法不能直接显示滑动面的发展过程,更不能显示滑面的受力、变形、破坏过程;强度折减法通过不断降低岩土强度使边坡逐渐达到极限破坏状态,直接得出滑面位置与安全系数,比较贴近工程实际。蔡文等[5]提出了二分法试算强度折减系数、破坏区域土体转化为坡面荷载方法、折减系数逐次变小的控制要求等概念来模拟计算边坡稳定性,验证了强度折减法的可行性,但没有给出明确的边坡失稳的判定准则。钟志辉等[6]提出采用局部强度折减法,将折减系数-位移曲线划分为匀速变形、加速变形、失稳3个变形阶段,匀速变形与加速变形交点处的位移确定为预警位移,加速变形与失稳阶段交点处的位移确定为极限位移,计算了边坡的位移,但没有提出边坡破坏准则和安全系数。邓华锋、任高峰等[7-8]采用了三维分析方法对大型边坡进行了稳定性分析研究,但均限于整体稳定性,没有给出每个单元的安全状态等。曾维国等[9]采用了Bishop法对露天矿山边坡稳定性进行了分析,却忽略了边坡空间形态对稳定性的影响。边坡越凹,破坏的可能性越大,边坡曲率半径、边坡高度和边坡角度对边坡稳定性都能产生较大影响,单纯的二维边坡稳定性分析得出的结论与实际情况相差很大,因此,对于深凹露天坑中的弧状边坡设计存在较大的优化空间。
笔者在研究和总结前人经验的基础上,引入安全度概念,获得每个计算单元的安全度,从而了解到边坡局部安全性,局部单元安全度与整体安全系数结合,更加合理地描述了边坡的安全稳定状态。
最后以某铁矿西南弧状边坡为例,采用Micromine、Dimine软件,创建边坡真三维模型[10],以FLAC3D为平台,采用FISH语言编制有限差分强度折减法、计算单元安全度和失稳准则等相关程序,较合理地分析了边坡的安全稳定性。
1 有限差分强度折减法原理显式有限差分法多用于多种材料模型和复杂边界连续介质力学问题的求解,与有限元法相比,在求解场的控制微分方程时,不需要形成庞大的刚度矩阵,具有计算速度快、求解量小、不存在计算收敛性的优点,对于非线性、大变形问题的求解更加有效,岩土质边坡具有大变形特征和材料的极不均一性,属于典型的高度非线性问题,因此,采用有限差分法分析边坡问题较有限元法具有很强的优势。
强度折减系数是指在施加载荷恒定的情况下,边坡内岩土体所发挥的最大抗剪强度与外荷载在岩土体内产生的剪应力的比值。从本质上来看,强度折减系数与极限平衡法中采用的边坡安全系数是一致的。
强度折减法[7-8]是将岩土体的抗剪强度指标C和φ,用一个折减系数Fs,如式(1)和式(2)所示的形式进行折减,然后,用折减后的抗剪强度指标CF和φF代替原来的抗剪强度指标C和φ,如式(3)所示。
| $ {C_F} = C/{F_s}, $ | (1) |
| $ {\varphi _F} = {\tan ^{-1}}(({\rm{tan}}\varphi )/{F_s}), $ | (2) |
| $ {\tau _{fF}} = {C_F} + \sigma {\rm{tan}}{\varphi _F}, $ | (3) |
式中:CF表示折减后岩土粘聚力,φF表示折减后岩土体内摩擦角,τfF表示折减后抗剪强度。
为了保证计算模型在开始计算时近似于弹性求解,折减系数Fs初始值通常取得足够小。此后不断增大折减系数Fs,使得折减后的抗剪强度指标不断减小,直至某个抗剪强度下边坡发生失稳破坏,发生失稳前所采用的折减系数即为边坡整体稳定系数。
2 失稳判据影响有限差分强度折减法分析边坡稳定性精确度的主要因素之一是失稳判据的选择[11-14],对于边坡达到极限平衡状态的判据,到目前为止并没有统一,主要有3种:①计算不收敛;②限定最大不平衡力与荷载的比值;③潜在滑移面塑性区贯通。其中:判据①②,在计算之前必须指定一定的迭代次数或比值,而迭代次数和比值的选择依赖于研究者的经验;判据③塑性区贯通的判据指标虽然直观,且力学意义明确,但如果塑性区贯通但节点速度不为零就不能判定边坡失稳,加之塑性区贯通很难从客观上确定,只能通过人的主观去判断,从而会导致结果存在一定的人为性。因此判据往往作为其他判据的补充。
文中提出采用最大节点位移时步曲线的收敛性作为边坡失稳的判据,当曲线不收敛时意味着边坡发生失稳,计算中对边坡材料强度逐步进行折减,直到曲线不收敛时的折减系数即为安全系数。计算的时长主要取决于安全系数折减的步长,即安全系数取值的精度。
3 单元安全度通常情况下,常用的计算程序只能分析出每个计算单元进入或没有进入塑性屈服阶段,但对于那些没有进入塑性屈服的单元,它的抗屈服能力无法获知。文中引入单元安全度从本质上能够表征每个单元与屈服面偏离的程度,可以表示单元材料抵抗进入塑性屈服的能力,加之文中前述有限差分强度折减法通过材料强度的折减找到最危险或最先破坏面,只能得到一个整体的边坡安全系数,对于边坡局部的情况无法获知,采用单元安全度与强度折减相结合的技术来分析边坡稳定性能够弥补强度折减法的不足,从而使分析的结果更加准确、全面。
研究采用摩尔库伦准则,它的屈服函数为
| $ f = {\sigma _1}-{\sigma _3}-({\sigma _1} + {\sigma _3}){\rm{sin}}\varphi-2c\cos \varphi {\rm{ = 0, }} $ | (4) |
定义单元的安全度为
| $ I = \frac{{({\sigma _1} + {\sigma _3}){\rm{sin}}\varphi + 2c\cos \varphi }}{{{\sigma _1}-{\sigma _3}}}, $ | (5) |
式中,f为屈服函数,σ1、σ3分别表示单元最大、最小主应力,c、φ分别表示岩土体的粘聚力、内摩擦角。
采用FISH语言根据安全度定义编制相应的程序,获取每个单元的最大、最小主应力、粘聚力和内摩擦角,计算出每个单元的安全度。当I>1时,单元处于安全状态,当I=1时,单元处于临界屈服状态,当I < 1时,单元进入塑性屈服状态。
4 实例分析 4.1 工程概况某铁矿属大型露天钒钛磁铁矿,设计规模1 000万t/a,露天开采终了境界在5~21勘探线之间,采场底标高1 320 m,最高采场台阶标高2 058 m (南帮),最大垂高738 m,采场上部尺寸2 000 m×1 600 m,下部尺寸800 m×90 m,1 650 m以上台阶高度为12 m,1 650 m以下台阶高度为15 m,台阶坡面角表土层为40°,矿、岩为65°。按3个一组设置最终边平台,每隔2个安全平台设置1个清扫平台,平台宽度在土层中为6 m、6 m、10 m,在矿岩中为4 m、4 m、10 m,边帮上运输平台宽度17 m。露天采场最终边坡角在土层中28°~31°,在矿岩中44°~47°。此露天矿开采形成的最终边坡属高陡露天坡,合理设置边坡参数对提高边坡的稳定性和降低采矿成本意义重大。
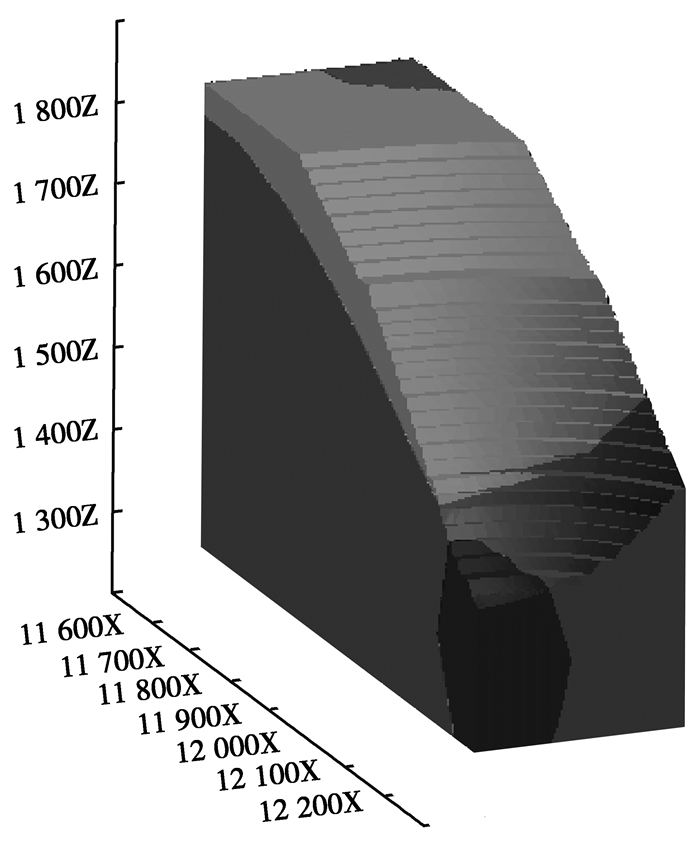
4.2 力学参数根据室内岩石力学试验,并经过相应力学参数工程处理,得到研究范围内岩体的物理力学参数指标,见表 1[15-16]所示。第四系表土层主要分布在边坡上部,垂直标高范围为1 650 m以上,辉长岩分布在整个第四系表土层以下的除矿体以外的所有区域,铁矿石未开采前从地表延伸至地下,开采后在露天坑1 350 m台阶向下延伸,详见图 2所示。
| 表 1 矿体及围岩物理力学参数 Table 1 Physical and mechanical parameters of ore and rock |
|
图 2 边坡三维地质体模型图 Figure 2 Three-dimensional geological model of slope |
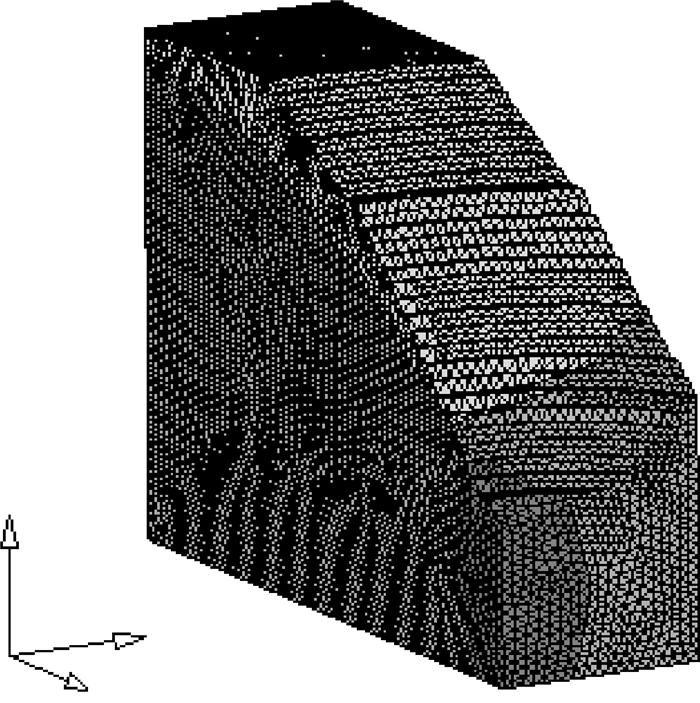
以FLAC3D为计算平台,采用DIMINE软件建立露天坑三维实体模型,见图 1所示。由图可见,露天坑形成的边坡大多为弧形边坡,对于弧形边坡采用三维分析稳定性的结果较二维分析结果更加接近实际,由于受计算机硬件的影响,本次计算模型为弧形边坡局部,加之四面体单元与六面体单元相比能够更精确地拟合边坡三维实体,因此,采用四面体对实体模型进行网格划分,三维实体弧形边坡分析力学计算部分见图 2所示,四面体划分网格后的模型见图 3所示。边坡模型长710 m,宽70 m,高750 m,创建后共形成273 684个单元和52 518个节点,模型底部及四周进行位移约束,边坡面和地表为自由面。

|
图 1 终了露天坑三维模型图 Figure 1 Three dimensional modal of open pit final boundary |
|
图 3 边坡三维四面体网格图 Figure 3 Grid map of 3D tetrahedron |
采用第2小节中讨论的失稳判据,结合FISH语言编制最大节点位移与折减系数计算程序,FISH语言编制的部分强度折减计算代码如下:
def SSR //定义了SSR函数,用来FLAC3D调用
ait1=0.02 //定义计算的精度
k11=1.00 //定义安全系数上限值
k12=3.50 //定义安全系数下限值
ks=(k11+k12)/2
loop while (k12-k11)>ait1
coh1=55.48e6/ks
coh2=5.29e6/ks
coh3=5.45e6
fri1=(atan ((tan (26.81*pi/180))/ks))*180/pi
fri2=(atan ((tan (38.8*pi/180))/ks))*180/pi
fri3=(atan ((tan (42.23*pi/180))/ks))*180/pi
command
model mohr
prop bulk 0.3e9 shear 1.8e8 coh coh1 fri fri1 ten 1e6 range group 1
prop bulk 44.4e9 shear 18.5e9 coh coh2 fri fri2 ten 20e6 range group 2
prop bulk 50.0e9 shear 20.83e9 coh coh3 fri fri3 ten 12.4e6 range group 3
fix x range x 11514.111516.1
fix x range x 12229.112231.1
fix y range y 87784.187786.1
fix y range y 88007.188009.1
fix z range z 1249.1 1251.1
ini dens 1810 range group 1
ini dens 2670 range group 2
ini dens 4100 range group 3
set grav 0 0-9.8
set mech ratio 9.8e-6
solve step 40000
endcommand
if mech_ratio < 1.0e-5
k11=ks
k12=k12
else
k12=ks
k11=k11
endif
ks=(k11+k12)/2
endloop
fosfile0=string (size1)+'_'+string (size2)+'_fos'+'.sav'
command
save fosfile0
endcommand
end
SSR
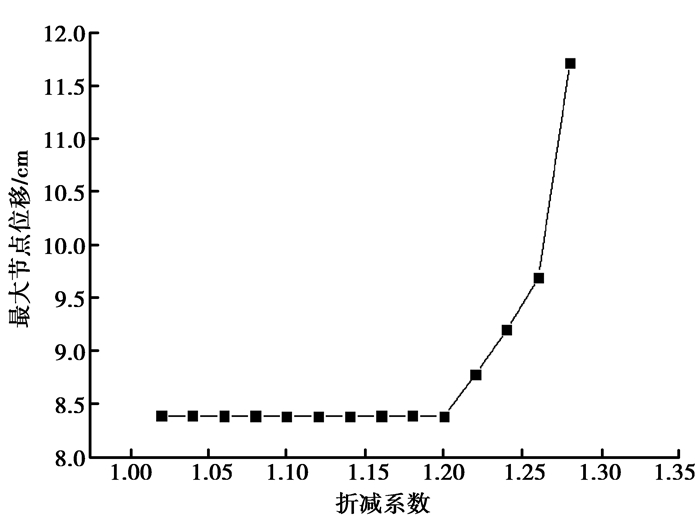
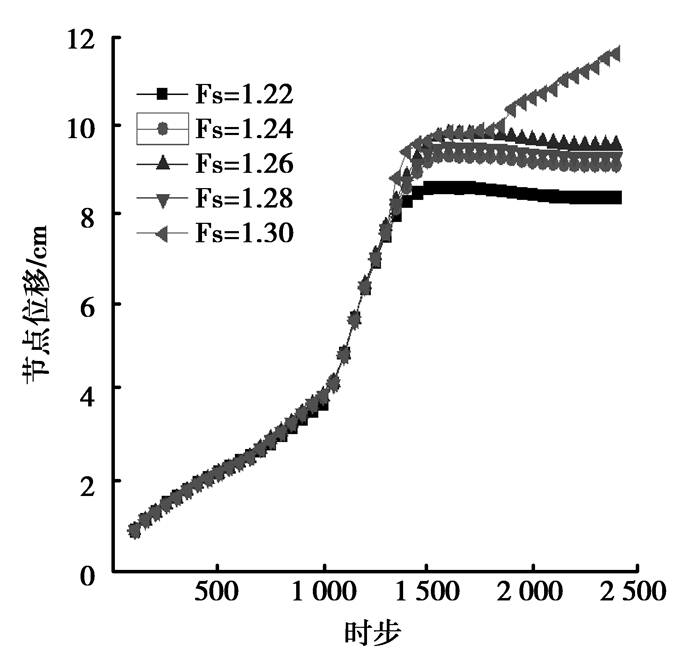
如图 4给出了折减系数从1.00~1.35之间的最大节点位移与折减系数的关系曲线,当折减系数在1.00~1.20范围内变化时,节点最大位移变化不大,当折减系数大于1.20时,最大节点位移变化较大,甚至发生不收敛现象。边坡的稳定性直接由最大节点位移的收敛性反映,如果位移收敛,边坡稳定,当折减系数大于某个值时,位移不收敛,边坡将发生失稳。图 4给出了折减系数的范围,针对范围内一定间隔的折减系数分别进行计算,得出图 5的结果,由图 5容易得出折减系数为1.30时,节点最大位移将随着计算时步不断加速增大,不再收敛,边坡发生失稳,由此得出该边坡整体稳定性系数为1.28(前述时步反映的是差分法迭代的过程,而不是物理上的时间)。此外,折减系数的精确度取决于迭代的间隔,间隔越小,精度越高。从图中可以看出最大节点位移-折减系数曲线发生了明显的突变,其原因是因为在某一个折减后的强度下,边坡发生了破坏失稳,导致最大节点位移迅速增加。
|
图 4 最大节点位移-折减系数关系图 Figure 4 Variation of maximum nodal displacementwith strength reduction factor |
|
图 5 节点最大位移-时步曲线 Figure 5 Nodal displacement with time steps |
得出边坡整体稳定性系数之后,根据单元安全度算法计算,得到图 6所示边坡的安全度分布图,边坡大部分计算单元安全度大于1,但在坡面局部出现了小于1的单元,这些地方包括:标高1 600 m至地表部分的南部台阶坡面、边坡顶部地表及境界底部坡角。对安全度小于1的单元进行显示,如图 7所示,坡顶位置处最小单元全度为0.823 77,在露天采矿过程中应针对安全度小于1的坡面位置采取合理的加固措施,根据边坡地质资料,出现安全度小于1的区域为边坡的第四系表土层,在以后设计过程中可优化表土层的坡面角。

|
图 6 单元安全度云图 Figure 6 The unites safety contours |

|
图 7 单元安全度小于1的云图 Figure 7 The contours unites safety less than 1 |
根据折减系数和单元安全度,从整体上分析出边坡的安全系数为1.28,能够满足采矿工程对边坡的安全要求,但局部坡面尤其是表土坡面局部单元安全度小于1,存在局部滑坡的可能。
5 结论1) 采用三维边坡计算模型能够解决二维边坡计算方法在圆弧状边坡计算中误差较大的问题,三维计算结果较符合实际。
2) 采用有限差分强度折减法计算三维边坡稳定性,与极限平衡法相比不需要事先假设滑动圆弧,而是通过逐渐折减边坡岩土材料强度参数,最终求得边坡整体的稳定性。
3) 每个计算单元引入安全度概念,分别计算各单元的安全度,从而能够得到整个边坡体安全度等值线,从安全度的角度能够获得边坡局部范围的安全可靠程度,弥补了采用有限差分强度折减法可能计算出三维边坡整体稳定而局部失稳的不足。
4) 采用最大节点位移时步曲线是否收敛作为边坡失稳的判据,能够简单、准确、唯一地得出边坡安全系数,弥补了采用其他判据由于人为指定容差所引起的较大误差。参考文献:
| [1] |
杨天鸿, 张锋春, 于庆磊, 等.
露天矿高陡边坡稳定性研究现状及发展趋势[J]. 岩土力学, 2011, 32(5): 1437–1452.
YANG Tianhong, ZHANG Fengchun, YU Qinglei, et al. Research situation of open pit mining high and steep slop stability and its developing trend[J]. Rock and Soil Mechanics, 2011, 32(5): 1437–1452. (in Chinese) |
| [2] | Šňupárek R, Konečný P. Stability of roadways in coalmines alias rock mechanics in practice[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2010, 2(3): 281–288. DOI:10.3724/SP.J.1235.2010.00281 |
| [3] | Ataei M, Bodaghabadi S. Comprehensive analysis of slope stability and determination of stable slopes in the Chador-Malu iron ore mine using numerical and limit equilibrium methods[J]. Journal of China University of Mining and Technology, 2008, 18(4): 487–493. |
| [4] | Zheng H. Eigenvalue problem from the stability analysis of slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2009, 135(5): 674–656. |
| [5] |
蔡文, 曹洪, 罗彦, 等.
强度折减有限元法模拟边坡牵引式破坏过程[J]. 岩石力学与工程学报, 2011, 30(S2): 3529–3533.
CAI Wen, CAO Hong, LUO Yan, et al. Simulation of retrogressive landslide fail use process by strength reduction fem[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 3529–3533. (in Chinese) |
| [6] |
钟志辉, 杨光华, 张玉成, 等.
基于局部强度折减法的土质边坡位移研究[J]. 岩土工程学报, 2011, 33(1): 196–201.
ZHONG Zhihui, YANG Guanghua, ZHANG Yucheng, et al. Displacement of soil slops based on local strength reduction method[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 196–201. (in Chinese) |
| [7] |
邓华锋, 李建林, 王乐华, 等.
基于强度折减法的库岸滑坡三维有限元分析[J]. 岩土力学, 2010, 31(5): 1604–1608.
DENG Huafeng, LI Jianlin, WANG Yuehua, et al. 3D finite element analysis of reservoir bank landside based on strength reduction method[J]. Rock and Soil Mechanics, 2010, 31(5): 1604–1608. (in Chinese) |
| [8] |
任高峰, 钱兆明, 闫振雄, 等.
基于轴比论的椭圆形深凹露天矿稳定性边坡形状确定方法研究[J]. 岩石力学与工程学报, 2012, 31(4): 675–680.
REN Gaofeng, QIAN Zhaoming, YAN Zhenxiong, et al. Study of determination method of stable slop shape for oval deep furrow open pits based on axial ratio theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(4): 675–680. (in Chinese) |
| [9] |
曾维国, 车兆学, 李旭, 等.
基于Bishop法的露天矿边坡稳定分析与实现[J]. 采矿与安全工程学报, 2012, 29(2): 265–288.
ZENG Weiguo, CHE Zhaoxue, LI Xu, et al. Analysis and implementation of surface mine slope stability based on bishop method[J]. Journal of Mining & Safety Engineering, 2012, 29(2): 265–288. (in Chinese) |
| [10] |
房智恒, 王李管, 熊张友.
基于Micromine-FLAC3D耦合技术的金属矿采矿扰动影响分析[J]. 采矿与安全工程学报, 2012, 29(6): 871–875.
FANG Zhiheng, WANG Liguan, XIONG Zhangyou. Mining disturbance analysis in metal mine based on micromin-FLAC3D coupling technology[J]. Journal of Mining & Safety Engineering, 2012, 29(6): 871–875. (in Chinese) |
| [11] |
翟友成, 曹文贵, 王江营, 等.
基于不确定型层次分析法的边坡稳定性模糊评判方法[J]. 岩土力学, 2011, 32(2): 539–543.
ZHAI Youcheng, CAO Wengui, WANG Jiangying, et al. Fuzzy evaluation method of slope stability based on uncertain analytic hierarchy process[J]. Rock and Soil Mechanics, 2011, 32(2): 539–543. (in Chinese) |
| [12] |
吴振君, 王水林, 葛修润.
LHS方法在边坡可靠度分析中的应用[J]. 岩土力学, 2010, 31(4): 1047–1054.
WU Zhenjun, WANG Shuilin, GE Xiurun. Application of Latin hypercube sampling technique to slope reliability analysis[J]. Rock and Soil Mechanics, 2010, 31(4): 1047–1054. (in Chinese) |
| [13] |
张菊连, 沈明荣.
水电边坡岩体稳定性分级系统研究[J]. 岩石力学与工程学报, 2011, 30(2): 3482–3490.
ZHANG Julian, SHEN Mingrong. Study of hydropower slope rockmass stability classification system[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 3482–3490. (in Chinese) |
| [14] |
夏世友, 张电吉, 夏亮, 等.
有限差分强度折减法求解边坡安全系数[J]. 武汉工程大学学报, 2012, 34(4): 19–26.
XIA Shiyou, ZHANG Dianji, XIA Liang, et al. Strength reduction finite difference method for solving safety factor of slope[J]. Journal of Wuhan Institute of Technology, 2012, 34(4): 19–26. (in Chinese) |
| [15] |
王旭春, 管晓明, 王晓磊, 等.
露天矿边坡稳定性与岩体参数敏感性研究[J]. 煤炭学报, 2011, 36(11): 1806–1811.
WANG Xucun, GUAN Xiaoming, WANG Xiaolei, et al. Study on stability of open-pit mine slope and sensitivity of rock mass parameters[J]. Journal of China Coal Society, 2011, 36(11): 1806–1811. (in Chinese) |
| [16] |
唐晓松, 郑颖人, 唐辉明.
边坡变形破坏演化特征的数值分析[J]. 重庆大学学报, 2013, 36(10): 101–113.
TANG Xiaosong, ZHENG Yingren, TANG Huiming. Numerical analysis on the evolutionary features of deformation and failure modes of slopes[J]. Journal of Chongqing University, 2013, 36(10): 101–113. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38

