2. 神华准能公司 黑岱沟露天煤矿,内蒙古 准格尔 010300
2. HeidaigouSurface Coal Mine, Shenhua Zhungeer Energy Corp., Jungar 010300, Inner Mongolia, P.R.China
大型煤田露天开采时通常采用分区开采,相邻采区间合理内排压帮高度及重复剥离深度的确定极为重要,严重影响内排运距、运输成本、内排空间、总体经济效益[1-4]。
露天矿分区开采时,相邻采区间必然存在公共边帮。为了缩短排土运距、减少外排征地、降低采矿成本,会在当前生产采区揭露最下层煤底板后开始内排,同时对相邻采区间公共边帮进行压帮。当剥采工程过渡到下一采区时,为回收相邻采区交接处的三角煤,需要对压帮量重复剥离[5-7]。不同的压帮高度,对应的重复剥离深度亦不同,故确定内排压帮高度的同时,也必须确定出重复剥离深度。
国内学者对露天矿内排压帮高度及重复剥离深度研究不是很多,曾有顾正洪等[4]采用相关费用最小法,得出了不同条件下最佳压帮高度的取值范围,对压帮高度的研究程度较为全面,未设计重复剥离深度;赵俊等[8]分析了近水平露天矿分区开采时全压帮、半压帮以及全留沟内排的特点,通过模型得到最佳留沟深度,其模型较为简单,未设计重复剥离深度;周伟等[9]考虑了一元三次函数两个极值点的特性,推导出了最佳压帮高度计算公式,得到端帮帮坡角与最佳压帮高度曲线,未设计重复剥离深度;赵彦合等[5]通过定义三角煤剥采比,建立了三角煤最佳采深的计算模型,确定平朔东露天矿全压帮内排条件下三角煤回收的最佳采深,但未设计内排压帮高度。笔者旨在建立简单且可靠的数学模型,采用费用补偿法及最小重复剥采比法对露天矿相邻采区间内排压帮高度及重复剥离深度进行综合优化。
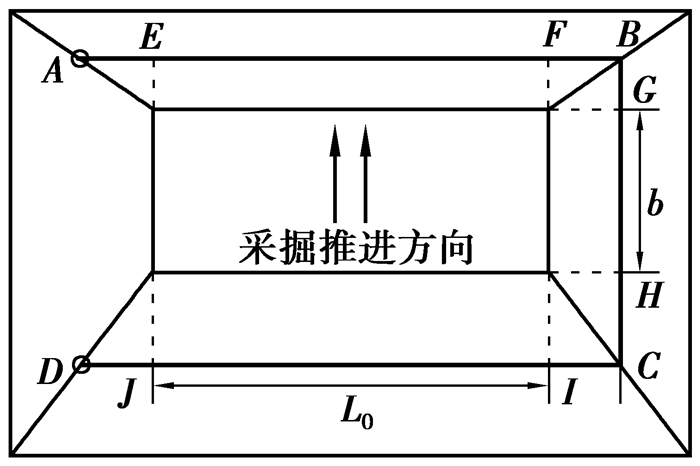
1 内排运距运距采用期望值法计算,即某水平内排运距等于该水平最长运距与最短运距的平均值[10-11]。露天矿内排方式根据运输线路分为单翼内排(俗称“单环”)和双翼内排(俗称“双环”),如图 1、2所示。
|
图 1 单翼内排运距示意图 Figure 1 Inner dumping haul distances of single circle |
|
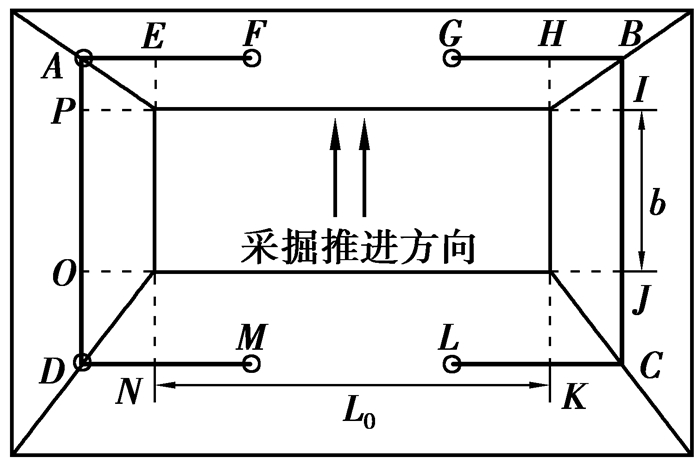
图 2 双翼内排运距示意图 Figure 2 Inner dumping haul distances of double circle |
单翼内排运距如图 1所示。最长运距(图 1中A→B→C→D)
所以,单翼内排运距
| $ {{L}_{\text{D}}}\text{=}\frac{1}{2}({{L}_{\text{Dc}}}+{{L}_{\text{Dd}}})={{L}_{0}}+b+\frac{1}{2}H(\text{cot}\ \alpha +\text{cot}\ \beta +2\text{cot}\ \gamma ), $ | (1) |
式中:LDc为最长单翼内排运距,m;LDd为最短单翼内排运距,m;LD为单翼内排运距,m;H为露天矿开采深度,m,H=hs+hc(hs为覆盖层平均厚度,hc为煤层平均厚度);L0为采掘或内排工作线长度,m;b为采掘工作帮与内排工作帮的坡底距离,m;α为采掘工作帮坡角,(°);β为内排工作帮坡角,(°);γ为端帮帮坡角,(°)。
1.2 双翼内排运距计算双翼内排运距如图 2所示。最长运距(图 2中G→B→C→L)
所以,双翼内排运距
| $ {L_{\rm{S}}}{\rm{ = }}\frac{1}{2}({L_{{\rm{Sc}}}} + {L_{{\rm{Sd}}}}) = \frac{1}{2}{L_0} + b + \frac{1}{2}H({\rm{cot}}\;\alpha + {\rm{cot}}\;\beta + {\rm{cot}}\;\gamma ), $ | (2) |
式中:LSc为最长双翼内排运距,m;LSd为最短双翼内排运距,m;LS为双翼内排运距,m;其他参数同上。
2 内排压帮高度所谓压帮是指露天矿相邻采区间的内排程度[8, 12]。压帮高度最小值为0 m,即全留沟;最大值为露天矿采深H m,即全压帮;压帮高度在0~H m之间时为半压帮。
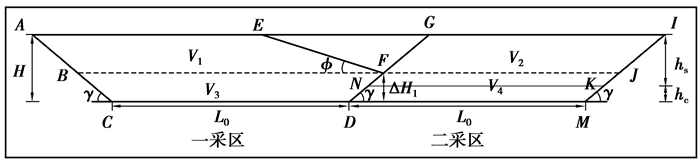
压帮的特点:压帮高度越大,内排空间越大,外排费用越低;压帮水平以上单翼运输内排运距大,压帮水平以下双翼运输内排运距小,故压帮高度越大,内排运距越短;转向过渡至新采区时,需要对压帮量重复剥离,故压帮高度越大,重复剥离量越大,重复剥离费越高。因此,需要综合优化确定经济效益最优的内排压帮高度[9, 13]。相邻采区各工程关系示意如图 3所示。
|
图 3 相邻采区工程关系示意图 Figure 3 Engineering relationship in adjacent mining area ΔH1-内排压帮高度, m; φ-压帮帮坡角, (°) |
压帮内排时,需单翼运输量有:一采区内排压帮水平以上内排量V1(四边形AEFB,m3),二采区内排压帮水平以上剥离量V2(四边形GIJF,m3);需双翼运输量有:一采区内排压帮水平以下内排量V3(四边形BFDC,m3),二采区内排压帮水平以下剥离量V4(四边形FJKN,m3)。
V1、V2、V3、V4计算公式:
| $ {{V}_{i}}={{S}_{i}}\cdot a,i=1~\sim 4 $ | (3) |
计算只用到V1和V2:
| $ \begin{array}{l} {V_1} = {S_1} \cdot a = \frac{1}{2}[({L_0} + \Delta {H_1} \cdot 2{\rm{cot}}\;\gamma + {L_0} + H \cdot 2{\rm{cot}}\;\gamma ) \times (H-\Delta {H_1})-\\ {(H-\Delta {H_1})^2}({\rm{cot}}\;\gamma + {\rm{cot}}\;\varphi )] \cdot a, \end{array} $ | (4) |
| $ {V_2} = {S_2} \cdot a = {L_0}(H-\Delta {H_1}) \cdot a。 $ | (5) |
全压帮时,V1对应内排量可采用双翼内排,运距为LS1(m),
所以,V1采用单翼运输相对双翼运输多增加运距为ΔL1(m),
| $ {L_1} = {L_{{\rm{D1}}}}-{L_{{\rm{S1}}}} = \frac{1}{2}{L_0} + \frac{1}{2}(H-\Delta {H_1}){\rm{cot}}\;\gamma 。 $ | (6) |
V2采用单翼运输相对双翼运输多增加运距为ΔL2(m),
| $ \Delta {L_2} = {L_{{\rm{D2}}}}-{L_{{\rm{S}}2}} = \frac{1}{2}{L_0} + \frac{1}{4}(H-\Delta {H_1}) \times ({\rm{cot}}\;\gamma + {\rm{cot}}\;\varphi )。 $ | (7) |
费用补偿法,是指半压帮相对全压帮所产生的运距增加值,能否通过减少重复剥离费及重复剥离运输费的折现得以补偿。
费用补偿法优点:1)消去计算压帮高度的非直接影响因素,简化计算公式;2)费用补偿法较相关费用最小法的最直接优点是进行两方案(半压帮与全压帮)对比,可信度更高。
通过计算费用补偿最小值求得内排压帮高度ΔH1,
| $ {\rm{min}}\;{F_{\rm{T}}} = {\rm{min}}\;f(\Delta {H_1}) = {\rm{min}}\;[{F_1} + ({F_2}-{F_3}-{F_4}){(1 + i)^{-t}}], $ | (8) |
式中:ΔH1∈[0,H];FT为费用补偿值,元;i为资金折现率,%;t为重复剥离时间,a。
若min FT>0,则此压帮高度条件下所产生的运距增加值,不能通过减少重复剥离费及重复剥离运输费的折现得以补偿,即全压帮更合理;若min FT=0,则此压帮高度条件下所产生的运距增加值,恰好能够通过减少重复剥离费及重复剥离运输费的折现得以补偿;若min FT < 0,则此压帮高度条件下所产生的运距增加值,足以通过减少重复剥离费及重复剥离运输费的折现得以补偿,为最优压帮高度。
全压帮重复剥离量
半压帮重复剥离量
| $ \begin{array}{l} {V_{\rm{R}}}({{\rm{m}}^3}), {V_{\rm{R}}} = \frac{1}{2}[{(H-\Delta {H_2})^2}({\rm{cot}}\;\tilde \omega + {\rm{cot}}\;\gamma )-{(H-\Delta {H_1})^2}, \\ ({\rm{cot}}\;\varphi + {\rm{cot}}\;\gamma )] \cdot a = \frac{1}{2}({\rm{cot}}\;\varphi + {\rm{cot}}\;\gamma ) \times [{(H-\Delta {H_2})^2}-{(H-\Delta {H_1})^2}] \cdot a。 \end{array} $ |
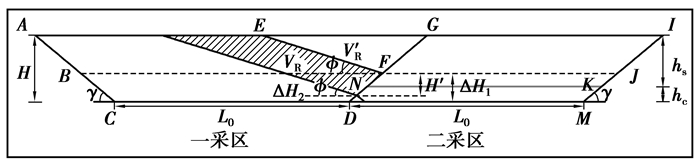
半压帮重复剥离量示意如图 4所示。
|
图 4 半压帮重复剥离量示意图 Figure 4 Repeated stripping amount of half covering H'1-内排压帮高度, m; Δh2-留三角煤高度, m |
半压帮相对全压帮减少的重复剥离量V′R(m3),
| $ V{'_{\rm{R}}} = {V_{{\rm{R}}0}}-{V_{\rm{R}}} = \frac{1}{2}{(H-\Delta {H_1})^2}({\rm{cot}}\;\phi + {\rm{cot}}\;\gamma ) \cdot \alpha 。 $ | (9) |
| $ {F_1} = \frac{{{V_1} \cdot \Delta {L_1} \cdot J}}{{1\;000}}。 $ | (10) |
将公式(4)、(6)代入计算得
| $ {F_1} = {A_1}\Delta H_1^3 + {B_1}\Delta H_1^2 + {C_1}\Delta {H_1} + {D_1}, $ | (11) |
式中:
| $ \begin{array}{l} {A_1} = - \frac{1}{{4\;000}}(3{\rm{cot}}{\;^2}\gamma + {\rm{cot}}\;\gamma {\rm{cot}}\;\varphi ) \cdot J \cdot a;\\ {B_1} = \frac{1}{{2\;000}}( - \frac{1}{2}H{\rm{cot}}{\;^2}\gamma + \frac{1}{2}H{\rm{cot}}\;\gamma {\rm{cot}}\;\varphi - \frac{5}{2}{L_0}{\rm{cot}}\;\gamma - \frac{1}{2}{L_0}{\rm{cot}}\;\varphi ) \cdot J \cdot a;\\ {C_1} = \frac{1}{{2\;000}}(\frac{3}{2}{H^2}{\rm{cot}}{\;^2}\gamma + \frac{1}{2}{H^2}{\rm{cot}}\;\gamma {\rm{cot}}\;\tilde \omega + H{L_0}{\rm{cot}}\;\gamma + H{L_0}{\rm{cot}}\;\tilde \omega - L_0^2) \cdot J \cdot a;\\ {D_1} = \frac{1}{{2\;000}}(H{L_0} + \frac{1}{2}{H^2}{\rm{cot}}\;\gamma - \frac{1}{2}{H^2}{\rm{cot}}\;\varphi )({L_0} + H\;{\rm{cot}}\;\gamma ) \cdot J \cdot a。 \end{array} $ |
| $ {F_2} = \frac{{{V_2} \cdot \Delta {L_2} \cdot J}}{{1\;000}}。 $ | (12) |
将式(5)、(7)代入计算得
| $ {F_2} = {A_2}\Delta H_1^3 + {B_2}\Delta H_1^2 + {C_2}\Delta {H_1} + {D_2}, $ | (13) |
式中:
| $ {F_3} = V{'_{\rm{R}}} \cdot {J_{\rm{R}}}。 $ | (14) |
将式(9)代入计算得
| $ {F_3} = {A_3}\Delta H_1^3 + {B_3}\Delta H_1^2 + {C_3}\Delta {H_1} + {D_3}, $ | (15) |
式中:
减少重复剥离量的运距LR(m),
| $ {L_{\rm{R}}}{\rm{ = }}\frac{1}{2}{L_0} + \frac{1}{2}b + \frac{1}{4}(H-\Delta {H_1}) \times ({\rm{cot}}\;\alpha + {\rm{cot}}\;\beta + 3{\rm{cot}}\;\varphi )。 $ | (16) |
| $ {F_4} = \frac{{V{'_{\rm{R}}} \cdot {L_{\rm{R}}} \cdot J}}{{1\;{\rm{000}}}}。 $ | (17) |
将式(9)、(16)代入计算得
| $ {F_4} = {A_4}\Delta H_1^3 + {B_4}\Delta H_1^2 + {C_4}\Delta {H_1} + {D_4}, $ | (18) |
式中:
| $ \begin{array}{l} {A_4} = - \frac{1}{{8\;000}}({\rm{cot}}\;\gamma + {\rm{cot}}\;\varphi ) \times ({\rm{cot}}\;\alpha + {\rm{cot}}\;\beta + {\rm{cot}}\;\varphi ) \cdot J \cdot a;\\ {B_4} = \frac{1}{{4\;000}}[({L_0} + b)({\rm{cot}}\;\gamma + {\rm{cot}}\;\varphi ) + \frac{3}{2}H({\rm{cot}}\;\gamma + {\rm{cot}}\;\varphi ) \times \\ ({\rm{cot}}\;\alpha + {\rm{cot}}\;\beta + {\rm{cot}}\;\varphi )] \cdot J \cdot a;\\ {C_4} = - \frac{1}{{4\;000}}[ - \frac{1}{2}{H^2}({\rm{cot}}\;\gamma + {\rm{cot}}\;\varphi ) \times ({\rm{cot}}\;\alpha + {\rm{cot}}\;\beta + {\rm{cot}}\;\varphi )\\ - H({\rm{cot}}\;\gamma + {\rm{cot}}\;\varphi )(2{L_0} + 2b)] \cdot J \cdot a;\\ {D_4} = \frac{1}{{8\;000}}[{H_2}({\rm{cot}}\;\gamma + {\rm{cot}}\;\varphi )({L_0} + b) + \\ \frac{1}{2}{H^3}({\rm{cot}}\;\gamma + {\rm{cot}}\;\varphi ) \times ({\rm{cot}}\;\gamma + {\rm{cot}}\;\beta + {\rm{cot}}\;\varphi )] \cdot J \cdot a \end{array} $ |
以上公式中,S1为V1所对应的剖面面积,m2;S2为V2所对应的剖面面积,m2;a为年推进度,m/a;J为单位运输成本,元/(m3·km);JR为重复剥离成本,元/m3;LR为减少重复剥离量的运距,m;F1为V1对应的运距增加费,元;F2为V2对应的运距增加费,元;F3为半压帮相对全压帮减少的重复剥离费,元;F4为半压帮相对全压帮减少的重复剥离量运输费,元;其他参数同上。
2.2.5 费用补偿值各项费用矩阵表示为
| $ \left( {\begin{array}{*{20}{c}} {{A_1}}&{{B_1}}&{{C_1}}\\ {{A_2}}&{{B_2}}&{{C_2}}\\ {{A_3}}&{{B_3}}&{{C_3}}\\ {{A_4}}&{{B_4}}&{{C_4}} \end{array}} \right)\left( \begin{array}{l} \Delta H_1^3\\ \Delta H_1^2\\ \Delta {H_1} \end{array} \right) = \left( \begin{array}{l} {F_1}-{D_1}\\ {F_2}-{D_2}\\ {F_3}-{D_3}\\ {F_4} - {D_4} \end{array} \right). $ | (19) |
所以,费用补偿值FT容易写成
| $ {F_{\rm{T}}} = {A_{\rm{T}}}\Delta H_1^3 + {B_{\rm{T}}}\Delta H_1^2 + {C_{\rm{T}}}\Delta {H_1} + {D_{\rm{T}}}。 $ | (20) |
FT是以ΔH1为自变量一元三次函数[14-15]。可利用一元三次函数图像及性质分析计算,求得FT的增减区间,进而得到FT取最小值时的内排压帮高度ΔH1。
由以上公式可以看出,影响FT结果的因素众多,包括:工作线长度,采掘工作帮坡角,内排工作帮坡角,端帮帮坡角,重复剥离帮坡角,采深,采场坑底宽度,吨公里运费,重复剥离费,重复剥离间隔年限,年水平推进度等。所以,各露天矿需针对其各项参数计算求得该矿最优的内排压帮高度。
3 重复剥离深度相邻采区间实行压帮内排,当新采区开采时必然存在二次剥离[5]。
重复剥采比(nR)是指露天矿相邻采区间采用压帮内排,当转向过渡至新采区时,需要重复剥离先前的压帮排弃量,而要回采重复剥离量所影响的煤炭时所必须的剥离量与这部分煤量的比值。即
| $ {n_{\rm{R}}} = \frac{{{S_{\rm{R}}} + {S_{\rm{n}}}}}{{{S_{\rm{c}}}}}, $ | (21) |
式中:nR为重复剥离剥剥采比,m3;SR为重复剥离量面积,m2;Sn为回采重复剥离影响的煤量时二采区的剥离量面积,m2;Sc为回采重复剥离影响的煤量面积,m2。
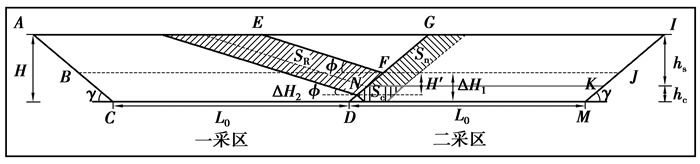
重复剥离剥剥采比各参数示意以及H′与ΔH1和Δh2关系如式(22)和图 5所示。
| $ H' = \Delta {H_1}-\Delta {H_2}。 $ | (22) |
|
图 5 重复剥离剥剥采比各参数示意图 Figure 5 Various parameters of repeated stripping ratio H'1-重复剥离深度, m; Δh2-留三角煤高度, m |
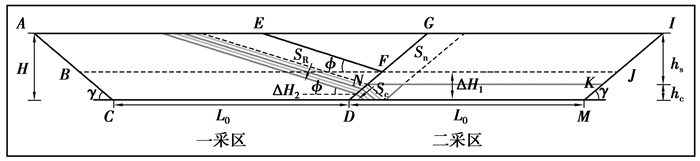
当重复剥离深度至煤层顶板,虽SR最少,但采区交接处留三角煤量最大,资源损失量最多,且此时nR不是最小,故经济效益不是最优;当重复剥离深度至煤层底板时,虽没有三角煤损失,可以回采重复剥离影响的全部煤量,但此时SR最大,nR不是最小,故经济效益也不是最优;当重复剥离深度至煤层顶、底板之间时,由图 6可以看出,随着重复剥离深度的增加,损失三角煤逐渐较少,Sc逐渐增加,SR也逐渐增加,Sn不变,nR处于变化中,因此,要使nR最小,需要采用数学模型计算确定。
|
图 6 不同重复剥离深度方案的煤、岩量变化示意图 Figure 6 Amount of coal and rock change by different repeated stripping depth |
重复剥离面积
| $ {S_{\rm{R}}} = \frac{1}{2}[{(H-\Delta {H_2})^2}-{(H-\Delta {H_1})^2}] \times ({\rm{cot}}\;\varphi + {\rm{cot}}\;\gamma )。 $ | (23) |
重复剥离影响煤量对应的二采区剥离面积
| $ {S_{\rm{n}}} = 2{h_{\rm{c}}}{h_{\rm{s}}}\cot \;\gamma 。 $ | (24) |
重复剥离影响的煤量面积
| $ {S_{\rm{c}}} = 2h_{\rm{c}}^2\cot \;\gamma-\frac{1}{2}\Delta H_2^2 \cdot 2\cot \;\gamma 。 $ | (25) |
所以,将式(23)、(24)、(25)代入式(21)计算得
| $ \begin{array}{l} {n_{\rm{R}}}{\rm{ = }}\left[ {\begin{array}{*{20}{l}} {\frac{1}{2}(\cot \;\gamma + \cot \;\varphi )\Delta H_2^2 - H(\cot \;\gamma + \cot \;\varphi )\Delta {H_2} + }\\ {\left( {H\Delta {H_1} - \frac{1}{2}\Delta H_1^2} \right)(\cot \;\gamma + \cot \;\varphi ) + 2{h_{\rm{c}}}{h_{\rm{s}}}\cot \;\gamma } \end{array}} \right]\\ /( - \cot \;\gamma \Delta H_2^2 + 2h_{\rm{c}}^2\cot \;\gamma ) \end{array} $ | (26) |
将nR对Δh2一阶导数得
| $ \begin{array}{l} n{'_{\rm{R}}} = \frac{{d({n_{\rm{R}}})}}{{d(\Delta {H_2})}} = \left[ {\begin{array}{*{20}{l}} { - H\cot \;\gamma (\cot \;\gamma + \cot \;\tilde \omega )\Delta H_2^2 + }\\ {2\cot \;\gamma [(H\Delta {H_1} - \frac{1}{2}\Delta H_1^2)(\cot \;\gamma + \cot \;\varphi ) + }\\ {h_{\rm{c}}^2 + 2{h_{\rm{c}}}{h_{\rm{s}}}\cot \;\gamma ]\Delta {H_2} - 2h_{\rm{c}}^2H\cot \;\gamma (\cot \;\gamma + \cot \;\varphi )} \end{array}} \right]\\ /{( - \cot \;\gamma \Delta H_2^2 + 2h_{\rm{c}}^2\cot \;\gamma )^2} \end{array} $ | (27) |
即
| $ n{'_{\rm{R}}} = A\Delta H_2^2 + B\Delta {H_2} + C。 $ | (28) |
n′R是以Δh2为自变量的一元二次函数。可利用一元二次函数图像及性质分析计算求得n′R的正负区间,即nR的增减区间,进而得到最小nR时的留三角煤高度Δh2,及重复剥离深度H′。
4 实例分析神华准格尔能源有限公司黑岱沟露天煤矿为大型近水平露天矿,采用分区开采,二采区和三采区为相邻采区。通过查看设计及咨询矿山技术员综合得出计算所需参数:煤层平均厚度hc=30 m,覆盖层厚度hs=110 m,采深H=140 m,采掘工作帮坡角α=5°,内排工作帮坡角α=16°,端帮帮坡角γ=35°,重复剥离帮坡角φ=20°,年推进度a=320 m/a,重复剥离时间t=17 a,单位运输成本J=1.93元/(km·m3),重复剥离成本JR=15元/m3,为采掘工作帮与内排工作帮的坡底距离b=100 m,工作线长度L0=2 150 m。
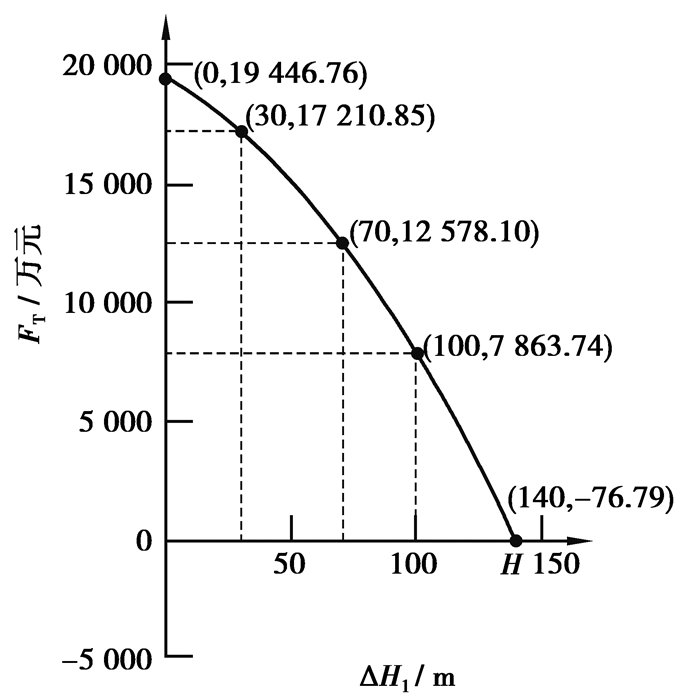
4.1 二采区内排压帮高度ΔH1将黑岱沟露天矿参数代入式(8)计算,绘制FT与压帮高度变化曲线如图 7所示,利用一元三次函数图像及性质分析得:FT图像的极大值与极小值均不在有效区间内,故在ΔH1∈(0,H)范围内为单调减区间,当ΔH1=135 m时,FT=0,此时,所产生的运距增加值恰好能够通过减少重复剥离费及重复剥离运输费的折现得以补偿;当ΔH1=140 m时,min FT为-76.79万元,所以,最合理压帮高度为ΔH1=140 m。
|
图 7 FT与压帮高度变化曲线 Figure 7 Curve of FT and covering height |
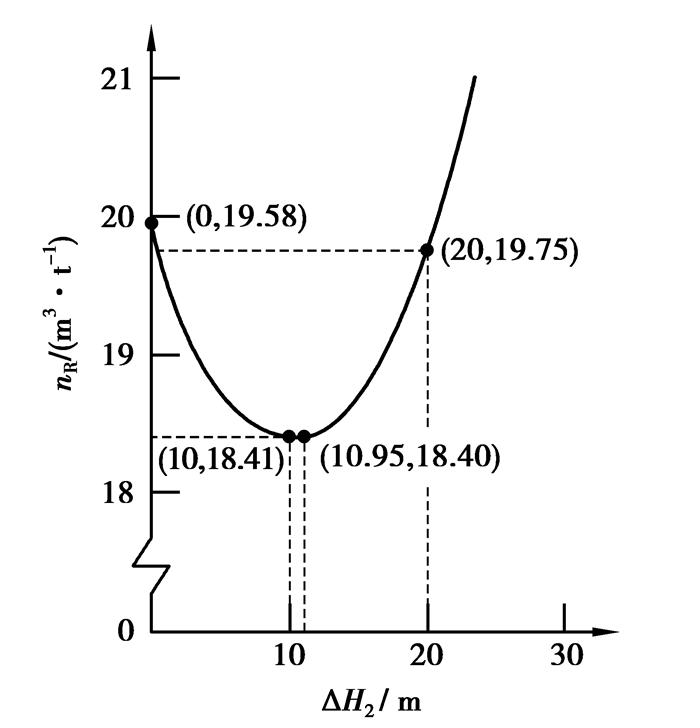
将黑岱沟露天矿参数代入式(21)计算,利用一元二次函数图像及性质求得nR最小值时的留三角煤高度Δh2=10.95 m,重复剥离深度H′=120.05 m。nR与留三角煤高度变化曲线如图 8所示。
|
图 8 nR与留三角煤高度变化曲线 Figure 8 Curve of nR and triangular coal height |
1)分析不同内排压帮方式内排运距的特点及计算原理,完成各项计算公式的推导;
2)分别建立内排压帮高度及重复剥离深度的数学模型。采用压帮水平以上单翼运输较双翼运输的运费增加值能否通过半压帮所减少的重复剥离费及重复剥离量运输费的折现值得以补偿作为确定压帮高度的有效判据,通过分析一元三次函数图像及性质,确定最优压帮高度ΔH1;定义重复剥采比nR,分析nR构成,利用一元二次函数图像及性质,确定nR最小值时的重复剥离深度H′及留三角煤高度Δh2。
3)绘制黑岱沟露天矿FT-ΔH1变化曲线及nR-Δh2变化曲线,确定最优内排压帮高度140 m,留三角煤高度10.95 m,重复剥离深度120.05 m。
| [1] |
才庆祥, 姬长生.
大型露天煤矿采区转向方式研究[J]. 中国矿业大学学报, 1996, 25(4): 45–49.
CAI Qingxiang, JI Changsheng. Research on min ing area steering mode of large opencast coal mine[J]. Journal of China University of Mining & Technology, 1996, 25(4): 45–49. (in Chinese) |
| [2] |
顾正洪, 李曙光.
近水平缓倾斜露天矿开采程序探讨[J]. 化工矿山技术, 1993, 22(1): 10–13.
GU Zhenghong, LI Shuguang. Research on min ing sequence for flat or gentle inclined surface mines[J]. Industrial Minerals & Processing, 1993, 22(1): 10–13. (in Chinese) |
| [3] |
曹博.复杂条件露天矿釆区转向及运排系统工程优化研究与应用[D].北京:中国矿业大学, 2012. CAO Bo.The optimization research and application of surface mine transition alternative mode of min ing area and transportation dumping engineering under complicated geological conditions[D].Beijing:China University of Mining ƃ Technology, 2012.(in Chinese) http://www.oalib.com/references/16329607 |
| [4] |
顾正洪, 查振高.
近水平矿床内排重要技术参数的确定[J]. 中国矿业大学学报, 1996, 25(3): 38–42.
GU Zhenghong, ZHA Zhengao. Decision of important technological parameters for in-pit waste dump in surface mine with a flat deposit[J]. Journal of China University of Mining & Technology, 1996, 25(3): 38–42. (in Chinese) |
| [5] |
赵彦合, 刘维玉, 陈杰, 等.
平朔东露天矿相邻采区重复剥离采深优化[J]. 露天采矿技术, 2012(S1): 59–60.
Zhao Yanhe, Liu Weiyu, Chen Jie., et al. Optimization on re-stripping depth of adjacent min ing area in Pingshuo East Open-pit Mine[J]. Opencast Coal Mining Technology, 2012(S1): 59–60. (in Chinese) |
| [6] |
才庆祥, 周伟, 车兆学, 等.
近水平露天煤矿端帮靠帮开采方式与剥采比研究[J]. 中国矿业大学学报, 2007, 36(6): 743–746.
CAI Qingxiang, ZHOU Wei, CHE Zhaoxue, et al. Research on the min ing method and stripping ratio of steep end-slope min ing in surface coal mines with flat coal deposit[J]. Journal of China University of Mining & Technology, 2007, 36(6): 743–746. (in Chinese) |
| [7] |
高鹏.
深凹露天矿实现内部排土提高经济效益[J]. 露天采矿技术, 2007(5): 7–8.
GAO Peng. Deep concave open-pit achieve inner dumping to raise economic benefit[J]. Opencast Coal Mining Technology, 2007(5): 7–8. (in Chinese) |
| [8] |
赵俊, 尚涛, 刘记鹏, 等.
近水平露天矿内排重复剥离量及留沟深度[J]. 金属矿山, 2012(2): 54–56.
ZHAO Jun, SHANG Tao, LIU Jipeng, et al. Inner dumping re-stripping volume and groove depth in near horizontal surface mine[J]. Metal Mine, 2012(2): 54–56. (in Chinese) |
| [9] |
周伟, 才庆祥, 李玉鹏, 等.
大型近水平露天煤矿内排压帮高度研究[J]. 煤炭科学技术, 2009, 37(1): 53–55.
ZHOU Wei, CAI Qingxiang, LI Yupeng, et al. Study on inner dumping covering height in large near horizontal surface mine[J]. Coal Science and Technology, 2009, 37(1): 53–55. (in Chinese) |
| [10] |
张幼蒂, 李克民. 露天开采优化设计理论与应用[M]. 徐州: 中国矿业大学出版社, 2000.
ZHANG Youdi, LI Kemin. Open-pit min ing optimization design theory and application[M]. Xuzhou: China Mining University Press, 2000. (in Chinese) |
| [11] |
于汝绶, 张瑞新, 王宝庭, 等. 露天采矿优化理论与实践[M]. 北京: 煤炭工业出版社, 2005.
YU Rushou, ZHANG Ruixin, WANG Baoting, et al. Open-pit min ing optimization theory and practice[M]. Beijing: Coal Industry Publishing House, 2005. (in Chinese) |
| [12] |
高永涛, 吴顺川. 露天采矿学[M]. 长沙: 中南大学出版社, 2010.
GAO Yongtao, WU Shunchuan. Open-pit min ing engineering[M]. Changsha: Central South University Press, 2010. (in Chinese) |
| [13] |
顾正洪, 李曙光, 张幼蒂.
近水平矿床留帮扩采方式的研究[J]. 中国矿业大学学报, 1995, 24(2): 59–63.
GU Zhenghong, LI Shuguang, ZHANG Youdi. Study of remained-slope min ing in surface mines with a flat-buried deposit[J]. Journal of China University of Mining & Technology, 1995, 24(2): 59–63. (in Chinese) |
| [14] |
罗永高, 陈一波.
三次函数的三大性质[J]. 中学数学杂志(高中版), 2005(3): 18–19.
LUO Yonggao, CHEN Yibo. The three Gunas of cubic function[J]. Middle School Mathematics Magazine (High School Edition), 2005(3): 18–19. (in Chinese) |
| [15] |
张国坤.
一元三次函数的图象和性质[J]. 中国数学教育, 2011(9): 39–42.
ZHANG Guokun. The image and properties for cubic functions of one variable[J]. Journal of Chinese Mathematics Education, 2011(9): 39–42. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38


