2. 辽宁久安安全技术咨询有限公司,沈阳 110027
2. Liaoning Safety Technology Consulting Co. Ltd., Shenyang 110027, P.R. China
中国许多煤田的水文地质条件十分复杂,在煤层开采过程中收到多种水体的威胁。近年来,随着矿井向深部延伸,华北地区开采煤层所承受的岩溶含水层水压越来越大,受底板突水的威胁也将更加严重,影响了矿井的安全生产[1]。底板突水事故是受隔水层厚度、水压、底板破坏深度等多种因素共同作用引起的[2]。在底板含水层水压、底板破坏深度等因素相同条件下,突水发生的危险会随着底板隔水层厚度的减小而增大;在隔水层厚度、底板破坏深度等因素相同条件下,突水发生的危险会随水压的增加而增大;在隔水层厚度和含水层水压等因素相同条件下,底板突水危险随底板破坏深度的增加而增大。在煤炭开采前,确定底板破坏深度,针对底板破坏深度与隔水层厚度和含水层水压的关系,设计合理的底板防水煤岩柱,可以预防底板突水事故的发生。
国内外许多学者采用现场测试法[3]、数值模拟法[4-5]、神经网络法[6]、多元线性回归法[7]、趋势面等方法对煤层底板破坏深度进行分析与预测的研究,如Tan等[3]通过对工作面底板离层的监测确定了底板破坏深度;段宏飞等[4]和Nemcik等[5]采用数值模拟方法分析确定了煤层底板的破坏特征和范围;Wang等[6]采用神经网络预测模型对采场底板破坏深度进行预测。上述模型和方法具有一定的优点,但也不同程度地存在不足,如:现场探测法耗费大量人力、物力;数值模拟法受参数的选择影响明显;BP神经网络法预测结果易陷入局部最优。上述方法不能很好的应用于工程实践,还需要探索出更加科学和使用的方法。
煤层底板破坏深度受多种因素共同影响,各因素之间又存在复杂的非线性关系,采用支持向量机(support vector machine, SVM)可以很好地解决这种非线性问题。在利用SVM进行预测的过程中,SVM参数C和g的选择对预测结果具有至关重要的影响。因此,笔者提出了一种人工蜂群算法(artificial bee colony algorithm, ABCA)和支持向量机相结合的底板破坏深度预测模型,该模型利用人工蜂群算法对SVM参数自动搜索和确定,以提高预测的效果。
1 煤层底板破坏深度影响因素如前所述,在隔水层厚度和含水层水压等因素相同条件下,底板突水危险随底板破坏深度的增加而增大,因此,下面的分析将不再考虑隔水层厚度和含水层水压的影响。煤层开采后,底板岩体受到采动影响,在工作面前方的底板受集中应力作用,集中应力超过底板岩体极限强度,引起底板破坏。底板破坏深度受应力条件、围岩性质和地质构造等共同影响,具体影响因素有:
1)开采深度。随着开采深度的增长,煤层的原岩应力变大,工作面开采后底板的应力集中更加明显,底板的破坏深度也就越大,呈现正比例关系[8]。
2)煤层倾角。煤层倾角影响着底板应力分布情况和应力集中程度,进而影响底板的破坏深度。据实测统计可知,倾角在4°~30°范围时,随倾角的增大底板破坏深度增大。
3)煤层开采厚度。煤层开采厚度越大,工作面的支撑压力就越大,底板的破坏深度也就越大。
4)工作面斜长。在一定范围内,工作面的斜长越长,顶板发生移动的岩层范围越大,矿山压力显现就越强烈。从国内众多学者的研究结果看,底板的破坏深度与工作面斜长呈线性或非线性关系,工作面越长,底板破坏深度越大。
5)底板抗破坏能力。在同样的条件下,底板的抗破坏能力越强,底板的破坏深度就越小。该指标是底板原生裂隙发育情况、岩层组合和岩石强度的综合体现。该指标按式(1)计算
| $ D = {R_{\rm{c}}} \cdot {C_1} \cdot \frac{{{C_2}}}{{15}}, $ | (1) |
式中:D为底板抗破坏能力;Rc为岩石抗压强度;C1为节理裂隙影响系数;C2为分层厚度影响系数。
6)断层。在断层附近,受到采用影响后,会使断层附近裂隙活化,增加底板破坏深度[9]。
2 SVM基本理论SVM是基本思路是将低维输入空间线性不可分的样本通过非线性映射算法转化至高维特征空间使其线性可分,进而对转化后的样本进行线性分析[10-11]。
假设样本为(x1, y1), (x2, y2), …(xk, yk)∈RN×R, 其中x1为输入参数,yk∈R为相应的输出参数,k为样本个数。支持向量机回归就是建立一个非线性映射θ,将数据x映射到高维特征空间F, 进而进行线性回归,回归函数为:f(x)=[ω·θ(x)]+b,其中b是阀值,ω是权值矢量。
根据统计理论[12-13],可通过以下目标数极小化确定支持向量机回归函数
| $ \begin{array}{l} R(\boldsymbol{\omega }) = {\rm{min}}\left[{\frac{1}{2}{\boldsymbol{\omega }^2}{\rm{ + }}C\sum\limits_{i = 1}^n {({\xi _i} + \xi _i^*)} } \right], \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l} {y_i} -f({x_i}) \le \varepsilon + {\xi _i}, \\ f({x_i}) -{y_i} \le \varepsilon + \xi _i^*, \\ {\xi _i}, \xi _i^* \ge 0. \end{array} \right. \end{array} $ | (2) |
式中,C为惩罚因子,其作用是对经验风险和模型复杂度进行折中;ξ和ξ*为非负松弛变量;ε为不敏感损失函数参数。
利用拉格朗日方法求解上述约束最优化问题,将原问题转化为其对偶问题,即
| $ \begin{array}{l} J({a_i}, a_i^*) = {\rm{max}}\left[{\frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n ( } {a_i}-a_i^*)({a_j}-a_j^*)K({x_i}, {x_j}) + \sum\limits_{i = 1}^n {a_i^*} ({y_i}-\varepsilon )-\sum\limits_{i = 1}^n {{a_i}} ({y_i}-\varepsilon )} \right], \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l} \sum\limits_{i = 1}^n {({a_i} -a_i^*)} = 0\\ 0 \le {a_i}, a_i^* \le C。 \end{array} \right. \end{array} $ | (3) |
式中,K(xi, xj)=[θ(xi)·θ(xj)]为支持向量机的核函数,ai, ai*为拉格朗日系数。
可得到SVM回归函数:
SVM的预测能力受惩罚因子C和核函数参数g影响明显。因此,需要对参数C和g进行参数寻优,从而获得具有较高预测精度的支持向量机。
人工蜂群算法(ABCA)是由土耳其学者Karaboga提出的一种模拟蜜蜂群体寻找优良蜜源的仿生智能计算方法[14]。ABCA中将蜜蜂分为采蜜蜂、观察蜂和侦查蜂3种不同工种。观察蜂和采蜜蜂的数量各占蜜蜂全体数量的一半。一处食物源对应一个采蜜蜂,即食物源的数量等于采蜜蜂的数量。如果某个食物源被采蜜蜂和观察蜂放弃,则该食物源对应的采蜜蜂变为侦查蜂。人工蜂群的搜索活动可概括如下:采蜜蜂根据记忆中的食物源位置在其邻域内确定一个新的食物源;采蜜蜂在回到蜂巢后将它们的食物源信息通过舞蹈与观察蜂共享,观察蜂根据采蜜蜂传回的信息对食物源进行优选;观察蜂根据选择的食物源在其邻域内搜索一个新的食物源;放弃食物源的采蜜蜂变为侦查蜂并开始搜索一个新的随机食物源。
ABCA-SVM中蜜源、引领蜂、跟随蜂的数目都是SN,按照上述ABCA搜索过程,对支持向量机的参数C和g进行参数寻优,算法的具体流程如下[15]:
1)算法控制参数初始化。设定终止迭代次数max-cycle,蜜源的最大搜索次数limit。
2)采用式(4)随机产生SN个蜜源,并与引领蜂相对应。每个蜜源的位置为优化问题的一个可能解Xi(i=1, 2, …, SN), Xi为由SVM参数C和g组成的2维向量。
| $ {x_{ij}} = {x_{j\min }} + {\rm{rand}}(0, 1)({x_{j\max }}-{x_{j\min }}), $ | (4) |
式中,xij为第i个蜜蜂第j维对应的搜索后的位置,xjmax、xjmin分别为第j维变量的上界和下界。
3)采蜜蜂根据式(5)做邻域搜索产生新解Vi。
| $ {v_{ij}} = {x_{ij}} + {r_{ij}}({x_{ij}}-{x_{kj}}), $ | (5) |
式中,i, k∈(1, 2, …, SN),j∈(1, 2)是随机选取的下标。rij∈[-1, 1]之间一个随机值,它控制xij邻域的范围,邻域的范围会随着搜索接近最优解逐渐减小。
4)计算蜂群中每个个体的适应度值,并在当前蜜源和新蜜源之间进行贪婪选择,如果搜索后的蜜源优于搜索前,则代替之前蜜源。采用函数
5)根据式(6)计算每个蜜源被选择的概率值Pi,跟随蜂以轮盘赌机制选择要跟随的蜜源进行采蜜,成为引领蜂,并在其附近按式(5)搜索新蜜源。
| $ {P_i} = \frac{{fit}}{{\sum\limits_{j = 1}^{{S_N}} {fi{t_j}} }}, $ | (6) |
式中,fiti是第i个解的适应度值。
6)搜索次数search=search+1,如果search < limit,则返回步骤(3);否则执行步骤(7)。
7)判别是否存在要放弃的蜜源。如果某些蜜源经limit次循环不变,则放弃该蜜源,且被放弃蜜源对应的引领蜂成为侦查蜂,按式(4)随机产生新蜜源。
8)迭代次数cycle=cycle+1,若满足条件cycle < max-cycle,则返回步骤(3),否则算法结束。
9)输出最佳适应度对应的SVM参数C和g,带入SVM模型对样本进行预测。
4 底板破坏深度的ABCA-SVM预测模型 4.1 输入参数的确定及数据采集为了验证笔者提出的ABCA-SVM底板破坏深度预测模型的有效性和实用性,选取采深H、煤层倾角α、采厚M、工作面斜长L、底板抗破坏能力D和是否有切穿断层或破碎带I作为影响底板破坏深度的主要影响指标,对我国部分矿井实测的底板破坏深度情况进行统计,统计结果见表 1。其中,在是否有切穿型断层这一指标中,1表示“有”,0表示“无”。选取样本1~25作为训练数据,样本26~30作为测试数据,用于对训练好的模型进行检验。采用平均绝对误差、平均相对误差、均方误差和平方相关系数作为预测性能的评价指标。
| 表 1 底板破坏深度样本数据 Table 1 Sample data of floor failure depth |
为了消除输入参数的量纲和量级不同对预测精度的影响,将全部样本数据采用数据归一化对样本数据进行标准化处理,采用式(7)归一化处理。
| $ T' = T{'_{\min }} + \frac{{T{'_{\max }}-T{'_{\min }}}}{{{T_{\max }}-{T_{\min }}}}(T-{T_{\min }}), $ | (7) |
式中:T是原始数据,Tmax、Tmin是原始数据的最大值、最小值;T′为归一化后的数据;T′max、T′min为归一化数据的最大值、最小值,分别取1和0。
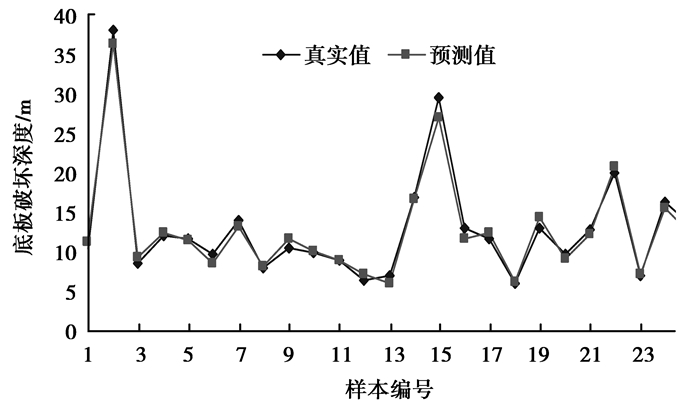
4.2 SVM参数寻优及预测结果分析底板破坏深度预测SVM模型中,输入向量为(H, α, M, L, D, I),输出为底板破坏深度,建立映射F(H, α, M, L, D, I)。选取径向基函数作为SVM回归预测模型的核函数,惩罚因子C和核参数g是该模型的两个重要参数,直接影响模型的预测性能。因此,采用人工蜂群算法对回归预测模型的参数C和g进行优化。ABCA的参数设置为:采蜜蜂的个数为20,迭代次数为200,C参数范围[0, 500],g参数范围[0, 100]。经过ABCA优化后,SVM模型的C和g分别为30.990 2和0.003 9。确定预测模型参数精辟,将其带入SVM模型中,由30组数据建立底板破坏深度预测模型,并进行底板破坏深度预测。预测结果见图 1和图 2所示。图 1为训练数据预测值和实际值的对比,图 2为测试数据预测值与实际值的对比。
|
图 1 ABCA-SVM模型训练集预测结果对比 Figure 1 Prediction result comparison ofABCA-SVM model for training set |
|
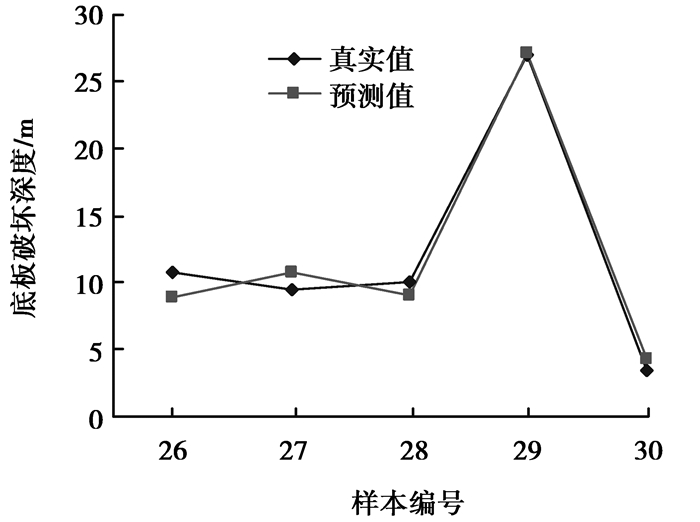
图 2 ABCA-SVM模型测试集预测结果对比 Figure 2 Prediction result comparison ofABCA-SVM model for test set |
由图 1可以看出,ABCA-SVM模型能够对训练数据进行很好拟合;由图 2可以看出,ABCA-SVM模型能够对测试数据进行很好的预测。上述可知,ABCA-SVM模型具有很强的预测和辨识能力,能够精确地对底板破坏深度进行预测。
为了对比ABCA-SVM模型的预测性能,采用多元线性回归模型、BP神经网络、PSO-SVM模型和GA-SVM模型对底板破坏深度进行预测,预测结果如表 2所示。各预测模型的输入变量、输出变量和样本数据均与ABCA-SVM相同。BP神经网络参数设置为:隐含层和输入层神经元的转移函数分别为tansig和logsig,训练函数为trainlm,最大训练次数为1 000次,训练误差为0.01,学习率为0.1。PSO-SVM模型参数设置为:粒子个数为20,学习因子c1=c2=2,ω=0.6,迭代次数为200,C和g的寻优分为分别为[0, 500]和[0, 100]。GA-SVM模型参数设置为:种群个数为20,交叉率为0.8,变异率为0.15,迭代次数为200,C和g的寻优分为分别为[0, 500]和[0, 100]。根据文献[14],可以确定多元线性回归模型为:
| $ h =-4.352\;9 + 0.012\;3H + 0.181\;5\alpha + 0.847M + 0.10{\rm{9}}\;{\rm{9}}L-7.645D + 7.275\;4I。 $ | (8) |
| 表 2 各模型预测结果 Table 2 Prediction results of each model |
由表 3可知,由表可知,ABCA-SVM模型预测样本的平均绝对误差为0.986 m,平均相对误差为12.5%,均方误差为0.005,这3个指标均小于其他预测模型,而平方相关系数略微低于PSO-SVM模型。总体上看,ABCA-SVM模型预测误差相对较小,模型的泛化能力较高,预测结果与实际数值相互吻合,可以用于底板破坏深度的预测。
| 表 3 各模型预测性能对比 Table 3 Prediction performance comparison of each model |
采用灰色关联分析的方法对底板破坏深度的主控因素进行了量化分析[16],确定了各影响因子由大到小的排序为:工作面斜长、煤层倾角、开采深度、底板岩层抗破坏能力、开采厚度和是否有切穿型断层。
5 结论1)采用人工蜂群算法对支持向量机的参数C和g进行优化,建立了ABCA-SVM的底板破坏深度预测模型。
2)选取采深、煤层倾角、采厚、工作面斜长、底板抗破坏能力和是否有切穿断层作为影响底板破坏深度的主要影响指标,采用ABCA-SVM预测模型对样本进行训练和预测,结果表明:模型具有较好的泛化能力和较强的预测功能,可以对底板破坏深度进行有效的预计。
3)底板破坏深度各影响因子由大到小的排序为:工作面斜长、煤层倾角、开采深度、底板岩层抗破坏能力、开采厚度和是否有切穿型断层。
| [1] |
赵铁锤. 华北地区奥灰水综合防治技术[M]. 北京: 煤炭工业出版社, 2006.
ZHAO Tiechui. Integrated control technique of ordovician limestone water in North China[M]. Beijing: China Coal Industry Publishing House, 2006. (in Chinese) |
| [2] | Zhang J C. Investigations of water inrushes from aquifers under coal seams[J]. International Journal of Rock Mechanics & Mining Sciences, 2005, 42: 350–360. |
| [3] | TAN Y L, ZHAN T B, XIAO Y X. In situ investigations of failure zone of floor strata in mining close distance coal seams[J]. International Journal of Rock Mechanics & Mining Sciences, 2010, 47: 865–870. |
| [4] |
段宏飞, 姜振泉, 张蕊, 等.
杨村煤矿综采条件下薄煤层底板破坏深度的实测与模拟研究[J]. 煤炭学报, 2011, 36(S1): 13–17.
DUAN Hongfei, JIANG Zhenquan, ZHANG Rui, et al. Field measurement and simulation research on failure depth of fully mechanized thin coal seam floor in Yangcun Coal Mine[J]. Journal of China Coal Society, 2011, 36(S1): 13–17. (in Chinese) |
| [5] | Nemcik J A, Indraratna B, Gale W. Floor failure analysis at a longwall mining face based on the multiple sliding block model[J]. Geotechnical and Geological Engineering, 2000, 18: 175–192. DOI:10.1023/A:1026533611345 |
| [6] | WANG Lianguo, ZHANG Zhikang, LU Yinlong, et al. Combined ANN prediction model for failure depth of coal seam floors[J]. Mining Science and Technology, 2009, 19: 684–688. |
| [7] |
施龙青, 徐东晶, 邱梅, 等.
采场底板破坏深度计算公式的改进[J]. 煤炭学报, 2013, 38(S2): 299–303.
SHI Longqing, XU Dongjing, QIU Mei, et al. Improved on the formula about the depth of damaged floor in working area[J]. Journal of China Coal Society, 2013, 38(S2): 299–303. (in Chinese) |
| [8] |
张蕊, 姜振泉, 李秀晗, 等.
大采深厚煤层底板采动破坏深度[J]. 煤炭学报, 2013, 38(1): 67–72.
ZHANG Rui, JIANG Zhenquan, LI Xiuhan, et al. Study on the failure depth of thick seam floor in deep mining[J]. Journal of China Coal Society, 2013, 38(1): 67–72. (in Chinese) |
| [9] |
陆银龙, 王连国.
含断层煤层底板损伤破坏演化数值模拟及微震监测研究[J]. 采矿与安全工程学报, 2013, 30(1): 38–44.
LU Yinlong, WANG Lianguo. Modeling and microseismic monitoring of damage and failure evolution of faulty coal seam floor[J]. Journal of Mining & Safety Engineering, 2013, 30(1): 38–44. (in Chinese) |
| [10] |
张振, 钮冰.
基于支持向量机回归的抗癌药物活性研究[J]. 计算机与应用化学, 2011, 28(11): 1377–1380.
ZHANG Zhen, NIU Bing. Predicting bis[J]. Computers and Applied Chemistry, 2011, 28(11): 1377–1380. (in Chinese) |
| [11] |
王春龙, 刘建国, 赵南京, 等.
基于支持向量机回归的水体重金属激光诱导击穿光谱定量分析研究[J]. 光学学报, 2013, 33(3): 314–319.
WANG Chunlong, LIU Jianguo, ZHAO Nanjing, et al. Quantitative analysis of laser-induced breakdown spectroscopy of heavy metals in water based on supprot-vector-machine regression[J]. Acta Optica Sinica, 2013, 33(3): 314–319. (in Chinese) |
| [12] |
王晓丹, 王积勤.
支持向量机研究与应用[J]. 空军工程大学学报:自然科学版, 2004, 5(3): 49–55.
WANG Xiaodan, WANG Jiqin. Research and application of support vector machine[J]. Journal of Air Force Engineering University:Natural Science Edition, 2004, 5(3): 49–55. (in Chinese) |
| [13] |
张学工.
关于统计学习理论与支持向量机[J]. 自动化学报, 2000, 26(1): 32–43.
ZHANG Xuegong. Introduction to statistical learning theory and support vector machines[J]. Acta Automatica Sinica, 2000, 26(1): 32–43. (in Chinese) |
| [14] |
郑伟, 刘静, 曾建潮.
人工蜂群算法及其在组合优化中的应用研究[J]. 太原科技大学学报, 2010, 31(6): 467–471.
ZHENG Wei, LIU Jing, ZENG Jianchao. Artificial bee colony algorithm and its application in combinatorial optimization[J]. Journal of Taiyuan University of Science and Technology, 2010, 31(6): 467–471. (in Chinese) |
| [15] |
李璟民, 郭敏.
人工蜂群算法优化支持向量机的分类研究[J]. 计算机工程与应用, 2015, 51(2): 151–155.
LI Jingmin, GUO Min. Study on classification of artificial bee colony algorithm to optimization of support vector machine[J]. Computer Engineering and Applications, 2015, 51(2): 151–155. (in Chinese) |
| [16] |
樊振丽, 胡炳南, 申宝宏.
煤层底板采动导水破坏带深度主控因素探究[J]. 煤矿开采, 2012, 19(1): 5–7.
FAN Zhenli, HU Bingnan, SHEN Baohong. Research on main factors of water-conductive fissure zone in floor induced by mining[J]. Coal Mining Technology, 2012, 19(1): 5–7. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38

