大量理论和实践表明,齿向修形能减小齿轮传动中啮入和啮出的冲击,改善载荷沿轮齿接触线不均匀分布的现象,减小振动和动载荷,提高齿轮传动精度、承载能力和使用寿命。孙建国等[1]利用ANSYS软件建立齿轮动力接触有限元模型进行分析,得出齿轮修形后啮入啮出冲击得到明显改善的结论;魏延刚[2]通过仿真证实了齿向修形可有效避免边缘效应, 大大降低齿轮传动中的最大应力。齿轮修形特别是齿向修形技术已得到越来越多的应用。
在齿向修形中,鼓形齿向修形因其实现方法简单、补偿受载变形效果好而被广泛采用[3]。然而,由于滚齿、蜗杆砂轮磨等连续展成法制齿工艺在加工齿向修形齿轮时,原理上存在几何误差,使齿面产生扭曲现象,并且扭曲会随着鼓形量及齿轮螺旋角的加大而越来越严重[4]。当前,一般只在某一高度(通常为齿高中间位置)测量齿向误差,结果不能反映齿面扭曲状况,故实际生产中齿面扭曲往往被忽略。
齿面扭曲会引起齿侧间隙变大、振动冲击增大、传动精度减小等问题,导致齿轮啮合效果变差、啮合噪声增加[5]。随着汽车、风电等行业对齿轮精度要求的进一步提高,一些精密传动系统明确提出了齿面扭曲的控制要求。郭二廓等[6]建立了成形磨齿齿向修形误差的数学模型,提出调整砂轮安装角以优化接触线的方法来改善齿面扭曲,但这种方法并不适用于蜗杆砂轮磨削;Tran等[7]提出磨削鼓形齿时增加一个齿轮的附加转角来减小齿向扭曲的方法,虽然效果较好,但是对机床的要求极高。目前,国外的研究集中于几大主要磨齿机生产厂商,通过修整出特定形状的蜗杆或增大磨削时的对角比来实现扭曲控制[8],但这种方法使参与磨削的蜗杆砂轮长度大为增加,导致一方面频繁修整砂轮,降低了加工效率;另一方面,砂轮的利用率大大降低,使磨齿成本大为提高。
为此,笔者提出了一种在齿轮修形曲线设计时即考虑加工扭曲问题的方法,以期采用常规蜗杆砂轮磨削工艺即可满足扭曲控制要求。该方法对于减小精密齿轮的制造成本、提高加工效率具有工程应用价值。
1 齿面扭曲的产生机理 1.1 齿面接触迹蜗杆砂轮磨齿本质上为一对螺旋齿轮啮合,砂轮与齿轮之间为点接触,齿面上接触点形成的轨迹就是接触迹。直齿齿面接触迹与渐开线重合,而斜齿齿面接触迹是一条倾斜曲线,且接触迹愈倾斜, 接触迹长度愈长, 齿面啮合有效部分增多, 相邻传动误差曲线重叠愈多, 齿面有效重合度愈大[9-10]。接触迹的形状只与所在齿轮齿廓面的固有参数(如基圆半径和螺旋角)有关,而与蜗杆砂轮的安装角或其他参数无关。同一条接触迹上的齿面磨削量相同,压力角也相同。在磨削过程中, 由齿顶转入齿面时,会出现啮合的不连续性,显然齿顶边缘和齿面接触迹之间夹角愈大啮合转换愈平稳。
1.2 齿面扭曲理想齿形在任何情况下载荷集中度都是最小的,要满足这种要求只有进行齿向修形,沿着齿轮齿向方向对齿面进行微量的修整,使其偏离理论的齿面。为了便于计算和加工,齿向修形常常采用特殊修形曲线,如圆弧线、抛物线、正弦曲线等。虽然修形曲线能改善齿向载荷不均匀现象,但同时又导致齿向方向产生不均匀的切除,使齿形压力角在齿向方向逐渐改变,即产生有害的“齿面扭曲”现象。在对直齿轮进行齿向修形时,工件轴与刀具轴垂直,接触迹与渐开线重合,齿向误差较小,修形后的鼓形与理论的鼓形曲线也较为接近,因此,几乎没有扭曲产生;但在斜齿轮磨削时,刀具沿着接触迹切除,而接触迹为斜线(见图 2), 刀具沿着修形曲线的轨迹运动,使同一高度处齿顶和齿根产生不同的磨削量,导致一端过修而另一端欠修,随着磨削量增大,扭曲的现象也越严重[11-12]。因此,齿面扭曲是所有带齿向修形的斜齿轮在磨齿过程中所特有的几何现象,这是制造原理所产生的误差。
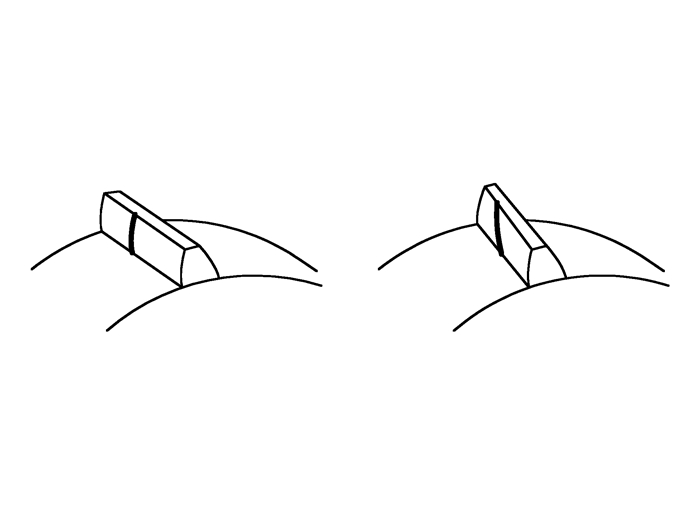
|
图 1 直齿轮(左)和斜齿轮(右)的齿面接触迹 Figure 1 Contact-trace of spur gear (left) and helical gear (right) |

|
图 2 齿轮齿向修形导致压力角变化 Figure 2 Tooth-trace modification causing the change of pressure angle |
计算修形齿轮误差的方法较多[13-14],但是针对齿面扭曲的计算扭曲量的方法还很少。标准渐开线齿轮在齿廓上的压力角处处相等[15],根据扭曲产生的机理,蜗杆砂轮磨削斜齿轮时,计算出同一高度上齿顶与齿根的磨削量之差就可以算出该高度上任意一点的扭曲量。
如图 3所示,取蜗杆砂轮与齿轮的一条啮合线用做计算,其啮合线的长度为B1B2。
| ${B_1}{B_2} = P{B_1} + P{B_2}, $ | (1) |
其中:
| $P{B_1} = \frac{{{r_{{\rm{b1}}}}\left( {\tan {\alpha _{{\rm{a1}}}}-\tan {\alpha _{o\tau 1}}} \right)}}{{\sin {\lambda _{{\rm{b1}}}}}}, $ | (2) |
| $P{B_2} = \frac{{{r_{{\rm{b2}}}}\left( {\tan {\alpha _{{\rm{a2}}}}-\tan {\alpha _{o\tau 2}}} \right)}}{{\sin {\lambda _{{\rm{b2}}}}}}, $ | (3) |
式中:rbi为基圆半径,
| ${r_{{\rm{b}}\;i}} = \frac{{{m_i}{z_i}\cos {\alpha _{{\rm{t}}\;i}}}}{{2\cos {\beta _i}}}, $ | (4) |
| $\tan {\alpha _{{\rm{t}}i}} = \frac{{\tan {\alpha _{{\rm{n}}i}}}}{{\cos {\beta _i}}}$ | (5) |
式中:αai为齿顶圆切向压力角,
| $\cos {\alpha _{{\rm{a}}i}} = \frac{{{r_{{\rm{b}}i}}}}{{{r_{{\rm{a}}i}}}}, $ | (6) |
式中:rai为齿顶圆半径;
式中:αoti为分度圆切向压力角,
| $\cos {\alpha _{{\rm{ot}}i}} = \frac{{{r_{{\rm{b}}i}}}}{{{r_{{\rm{o}}i}}}}, $ | (7) |
式中:roi为分度圆半径;
式中:λbi为基圆导程角,
| ${\lambda _{{\rm{b}}i}} = {90^ \circ }-{\beta _{{\rm{b}}i}}, $ | (8) |
| $\tan {\beta _{{\rm{b}}i}}\cos {\alpha _{{\rm{t}}i}}.$ | (9) |
i=1或2,i=1表示蜗杆砂轮,i=2表示齿轮。
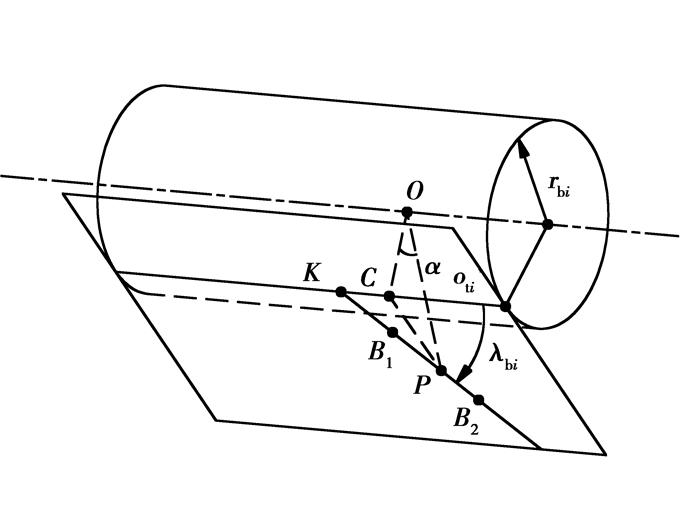
|
图 3 蜗杆砂轮与齿轮的啮合线 Figure 3 Mesging lines of worm wheel and gear (i=1表示蜗杆砂轮,i=2表示齿轮) |
啮合线沿齿向方向的长度为l。
| $l = {l_1} + {l_2}, $ | (10) |
其中:
| ${l_1} = P{B_1}\cos {\lambda _{{\rm{b2}}}}, $ | (11) |
| ${l_2} = P{B_2}\cos {\lambda _{{\rm{b2}}}}.$ | (12) |
将齿轮齿面展开成平面,如图 4所示。抛物线M1、M2分别为左右齿面的修形曲线,EF为齿面上的接触迹,上面任意一点的扭曲量都相等。A位于齿顶,F位于齿根,AC长度为l1,DF长度为l2。P2点的扭曲量为F点与A点的鼓形量之差,即P2点的扭曲量可由P3点的鼓形量减去P1点的鼓形量计算得出。
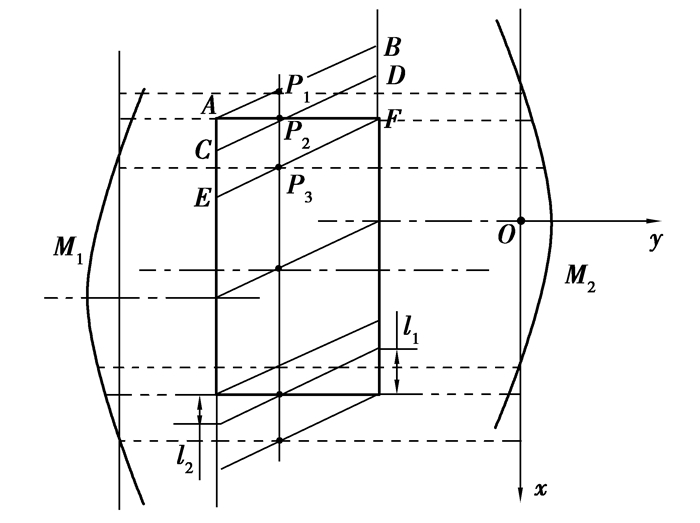
|
图 4 斜齿轮沿齿面展开示意图 Figure 4 Dchematic diagram of helical gear unfolding longitudinally |
建立如图 4所示的xOy坐标系,设最大鼓形量为cp,齿宽2l,齿向上H点的x坐标为h,若修形曲线为抛物线,则曲线M2可表示为
| $y = f\left( x \right) =-\frac{{cp}}{{{l^2}}}{x^2} + cp, $ | (13) |
曲线上任意点H点的鼓形量为
| $f\left( h \right) = cp-cp{\left( {\frac{h}{l}} \right)^2}, $ | (14) |
H点的扭曲量T为
| $T = f\left( {h + {l_1}} \right)-f\left( {h-{l_2}} \right), $ | (15) |
将式(14)代入式(15)得:
| $T =- cp\left[{\frac{{2\left( {{l_1} + {l_2}} \right)}}{{{l^2}}}h + \frac{{l_1^2-l_2^2}}{{{l^2}}}} \right].$ | (16) |
由式(16)可知,影响齿面扭曲量大小的主要因素是齿轮与砂轮的固有参数和修形曲线的鼓形量,由于鼓形量的存在,齿轮齿向方向各点的修形量不等,导致不同高度的扭曲量也不同。将齿轮齿向冲程离散,计算出每一离散点处的扭曲量,并将各点处扭曲量绘制出来,即齿向扭曲量的变化趋势。如图 5所示,当修形曲线为抛物线时,扭曲量的变化趋势为一条过零点的斜直线,在齿宽方向扭曲量由正的最大值向负的最大值变化,越靠近齿轮端面,齿向扭曲越严重。取不同的齿轮螺旋角和修形最大鼓形量进行计算,对比得到图 5(a)、(b)的图形。由图可知,修形曲线的中心鼓形量越大,齿轮的螺旋角越大,扭曲越严重。
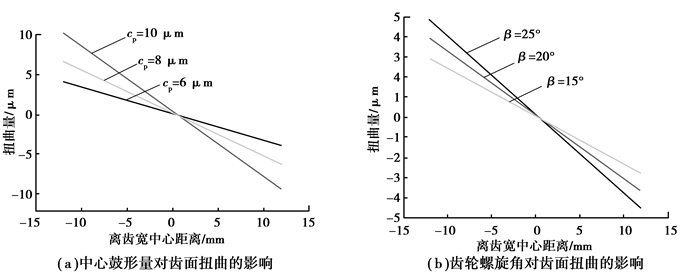
|
图 5 中心鼓形量和齿轮螺旋角对齿面扭曲的影响 Figure 5 Central crownings and gear helical angle's influence on gear twist |
齿轮传动的理想情况是齿轮在齿向全长上都接触到,但这种理想啮合情况难以实现,由于齿轮制造的偏差、齿轮安装的误差和接触变形等因素,实际齿轮在啮合时可能只有一个点或一小段相接触[16]。为此,生产实际中常将齿轮齿向曲线设计成鼓形,使齿向中心满足一定的鼓形量。由式(16)可知,当修形曲线为一条直线,即没有齿向修形时,cp=0,没有扭曲现象;随着鼓形量增加,齿向磨削量增大,扭曲量随之变大。鼓形量是齿向修形的一个主要参数,但是关于鼓形量的选用,并没有统一标准。通常根据经验设计最大鼓形量[17],最常用的是采用抛物线进行修形,抛物线的顶点即为最大鼓形量处,也称为鼓点,鼓点处的鼓度值即为最大鼓形量。
由图 6可知,齿轮端面的位置扭曲量最大,要设计出既满足鼓形量的要求又使整个齿向扭曲量变化尽可能小的修形曲线,需保持中间的鼓形量大小,对齿宽两端一定长度范围内的曲线倾斜度减缓。
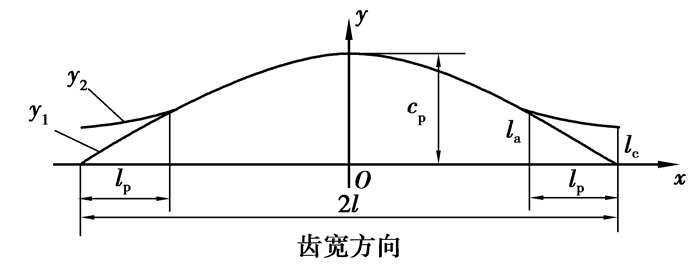
|
图 6 修形曲线的改进 Figure 6 Improvement of modification curve |
将齿面沿齿宽方向展开,标准渐开线齿轮的齿面为平面,齿宽方向投影为直线,鼓形修形曲线为抛物线y1。建立如图 6所示的坐标系,最大鼓形量为cp,齿宽为2l,将齿宽两端距离lp长度范围内的曲线鼓形量减小,长度比例因子为λ=lp/l;端面处修形量减少lc,减缓比例因子为t=lc/la。根据需要将修形曲线分为3段,分别为齿轮左端面扭曲减缓区-l-l2≤x < (λ-1) l,中间鼓形区(λ-1)l≤x < (1-λ) l,右端面扭曲减缓区(1-λ)l≤x < l+l1,下面构建新的修形曲线y2。
由式(13),修形曲线y1的表达式为
| ${y_1} = {f_1}\left( x \right) =-\frac{{cp}}{{{l^2}}}{x^2} + cp, $ | (17) |
其中:-l≤x≤l。
则修形曲线各段分别为
| $当\left( {\lambda-1} \right) \le x < \left( {1-\lambda } \right)l时, {y_2} = {y_1};$ | (18) |
| $当-l \le x < \left( {\lambda-1} \right)l或\left( {\lambda-1} \right)l \le x < l时, {y_2} = \left( {1 - t} \right){y_1} + {l_{\rm{c}}}.$ | (19) |
其中λ, t∈[0, 1]。因此,修形曲线y2的表达式为
| ${y_2} = {f_2}\left( x \right) = \left\{ \begin{array}{l} cp\left( {1- \frac{1}{{{l^2}}}{x^2}} \right), \left( {\lambda- 1} \right)l \le x < \left( {1- \lambda } \right)l;\\ cp\left[{\left( {1-t} \right)\left( {-\frac{1}{{{l^2}}}{x^2}} \right) + 1-t{{\left( {1 - \lambda } \right)}^2}} \right], \\-l -{l^2} \le x < \left( {\lambda -1} \right)l或\left( {1 - \lambda } \right)l \le x < l + {l_1}. \end{array} \right.$ | (20) |
由式(15)可知,齿向方向任意点x处扭曲量为
| $T = {f_2}\left( {x + {l_1}} \right)-{f_2}\left( {x-{l_2}} \right).$ | (21) |
根据图 5(a),抛物线越倾斜(鼓形量越大),扭曲量越大。因此,随着lc变大,即t变大,抛物线越平缓,扭曲量越小;同理,当λ变大(即lp增大),抛物线越平缓,扭曲量越小。根据扭曲量的计算方法,调整比例因子λ和t的大小就可以得到最合适的修形曲线。
4 计算实例蜗杆砂轮和齿轮的基本参数见表 1,齿轮为右旋渐开线圆柱斜齿轮,齿轮宽度2l=24 mm,则l=12 mm。用蜗杆砂轮进行加工,砂轮宽度180 mm,鼓形量大小cp取8 μm,比例因子分别取λ=0.15,t=0.8。
| 表 1 蜗杆砂轮与齿轮的基本参数 Table 1 Parameters of worm wheel and gear |
由式(11)、(12),计算出:
l1=2.75 mm,l2=2.13 mm。
由式(20),分段修形曲线为
| $f\left( x \right) = \left\{ \begin{array}{l} - \frac{1}{{18}}{x^2} + 8, x \in \left[{-10.2, 10.2} \right];\\ - \frac{1}{{90}}{x^2} + 3.376, x \in \left[{-14.13, -10.2} \right] \cup \left[{10.2, 14.75} \right]. \end{array} \right.$ | (22) |
由式(15),修形后齿向方向扭曲量T为
| $T = f\left( {h + 2.75} \right)-f\left( {h-2.13} \right), $ | (23) |
其中:h∈[-12, 12]。
由式(22)、(23),可得:
| $T = \left\{ \begin{array}{l} - 0.044{h^2}- 0.353h + 4.254, h \in \left[{- 12, - 8.07} \right);\\ - 0.542h - 0.168, h \in \left[{- 8.07, 7.45} \right);\\ 0.044{h^2}- 0.298h- 4.456, h \in \left[{7.45, 12} \right]. \end{array} \right.$ | (24) |
对齿向方向进行离散,计算各个点的扭曲量大小,利用MATLAB软件进行仿真,得到修形后扭曲量沿齿向方向的变化趋势,如图 7所示。
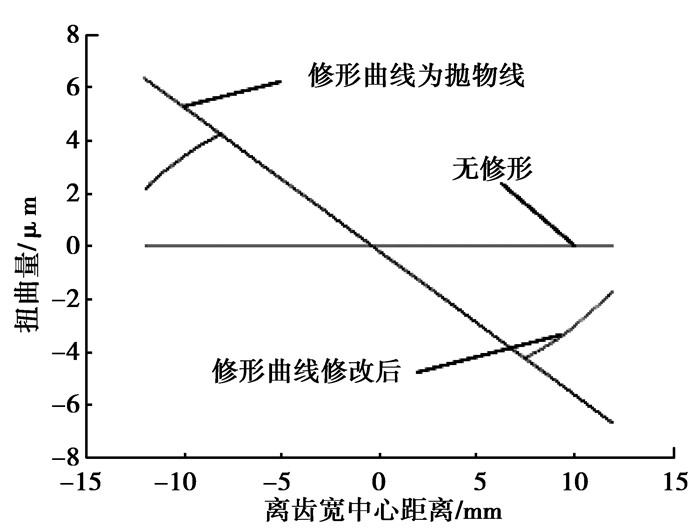
|
图 7 修形前后齿向方向扭曲量对比图 Figure 7 Comparison diagram of the lengthwise gear distortion before and after modification |
1) 蜗杆砂轮磨削斜齿轮时,齿轮压力角从一段到另一段逐渐变化,产生齿面扭曲现象,齿轮螺旋角、修形曲线鼓度越大,齿面扭曲越严重,齿面扭曲是蜗杆砂轮磨削齿向修形的斜齿轮特有的几何现象。
2) 给出了一种齿面扭曲的计算方法,根据同一条渐开线上齿顶与齿根修形量的不同,求出鼓形量的差值,以此计算出扭曲量。
3) 提出了一种修形曲线的改进设计方法,通过调整比例因子和鼓度,减缓齿向两端扭曲量,实现在设计阶段消减齿面扭曲的目的。
| [1] |
孙建国, 林腾蛟, 李润方, 等.
渐开线齿轮动力接触有限元分析及修形影响[J]. 机械传动, 2008, 32(2): 57–59.
SUN Jianguo, LIN Tengjiao, LI Runfang, et al. Dynamic contact finite element analysis of involute gear s and the influence of modification[J]. Journal of Mechanical Transmission, 2008, 32(2): 57–59. (in Chinese) |
| [2] |
魏延刚.
渐开线直齿圆柱齿轮的边缘效应与齿向修形初探[J]. 中国机械工程, 2011, 22(12): 1413–1417.
WEI Yangang. Research on Edge Effect and Longitudinal Modification of Involute Spur Cylindrical Gear Pairs[J]. China Mechanical Engineering, 2011, 22(12): 1413–1417. (in Chinese) |
| [3] |
周志峰, 刘伟, 王婧.
渐开线直齿轮修形的有限元分析与研究[J]. 机电工程, 2013, 30(12): 1490–1493.
ZHOU Zhifeng, LIU Wei, WANG Jing. Finite element analysis and research on involute spur gear modification[J]. Journal of Mechanical and Electrical Engineering Magazine, 2013, 30(12): 1490–1493. (in Chinese) |
| [4] |
辛经纬, 王生泽.
齿轮修形及其实现方法研究[J]. 机械机械, 2009, 36(5): 19–21.
XIN Jingwei, WANG Shengze. Research on the gear's modification and its processing[J]. Machinery, 2009, 36(5): 19–21. (in Chinese) |
| [5] |
李特文. 齿轮几何学与应用理论[M]. 上海: 上海科学技术出版社, 2008.
Litvin F L. Gear geometry and applied theory[M]. Shanghai: Shanghai Science and Technology Press, 2008. (in Chinese) |
| [6] |
郭二廓, 黄筱调, 方成刚, 等.
一种提高成形磨齿齿向修形精度的接触线优化方法[J]. 计算机集成制造系统, 2014, 20(1): 134–141.
GUO Erkuo, HUANG Xiaodiao, FANG Chenggang, et al. Contact lines optimization method for improving tooth-trace modification accuracy of form grinding[J]. Computer Integrated Manufacturing Systems, 2014, 20(1): 134–141. (in Chinese) |
| [7] | Tran V T, Hsu R H, Tsay C B. Study on the anti-twist helical gear tooth flank with longitudinal tooth crowning[J]. Journal of Mechanical Design, 2014, 136(6): 682–694. |
| [8] |
夫尔斯提切.在特定齿面线隆起处用特定扭曲来形成齿面的对角展形方法: CN101310906 B[P].2008-11-26. Gleason. Diagnal generating method to generate tooth flanks with specified twist at specified flank line crowning:CN101310906 B[P].2008-11-26.(in Chinese) |
| [9] |
李铭忠, 朱坚明, 郭二廓, 等.
变位渐开线斜齿圆柱齿轮接触线长度参数化计算[J]. 机械设计与制造, 2013(3): 219–222.
LI Mingzhong, ZHU Jianming, GUO Erkuo, et al. Parametric Calculation for Contact Line Length of Involute Helical Modified Gears[J]. Machinery Design and Manufacture, 2013(3): 219–222. (in Chinese) |
| [10] |
周志峰.渐开线圆柱直齿轮修形的分析与研究[D].北京:北京交通大学, 2014. ZHOU Zhifeng. Analysis and Research on Modification Involute Spur Gear[D]. Beijing:Beijing Jiaotong University, 2014. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10004-1014178286.htm |
| [11] | Faulstich I. Diagonal generating method to generate tooth flank with specified twist at specified flank line crowning:US, US7937182 B2[P]. 2011-05-03. |
| [12] | StadtfeldH J, Mundt E G. Threaded grinding wheel and method of dressing:US006217409B1[P]. 2001-04-17. |
| [13] |
李国龙, 林超, 李先广, 等.
成形磨齿砂轮包络计算的双参数点矢量族法[J]. 重庆大学学报, 2013, 36(4): 11–18.
LI Guolong, LIN Chao, LI Xianguang, et al. Envelope to a two-parameter family of point vectors method for surface swept by wheel during 5-axis gear form grinding[J]. Journal of Chongqing University:Natural Science Edition, 2013, 36(4): 11–18. (in Chinese) |
| [14] |
李国龙, 李先广, 刘飞, 等.
拓扑修形齿轮附加径向运动成形磨削中的砂轮廓形优化方法[J]. 机械工程学报, 2011, 47(11): 155–162.
LI Guolong, LI Xianguang, LIU Fei, et al. Method of profile optimization of a form grinding with additional radial motion of topologically modified gear[J]. Journal of Mechanical Engineering, 2011, 47(11): 155–162. DOI:10.3901/JME.2011.11.155 (in Chinese) |
| [15] |
梁锡昌, 邵明, 吉野英弘. 齿轮及其刀具制造的研究[M]. 重庆: 重庆大学出版社, 2001.
LIANG Xichang, SHAO Ming, Yoshino Eihiro, et al. Research of gear and its cutting tool's manufacture[M]. Chongqing: Chongqing University Press, 2001. (in Chinese) |
| [16] |
师军伟, 王小林, 汤清双, 等.
基于MATLAB的交错轴斜齿轮接触迹分析[J]. 机械传动, 2012, 36(11): 93–95.
SHI Junwei, Wang Xiaolin, Tang Qingshuang, et al. Analysis of crossed helical gears contact path by using MATLAB[J]. Journal of Mechanical Transmission, 2012, 36(11): 93–95. (in Chinese) |
| [17] |
周广森.渐开线圆柱齿轮修形设计研究[D].沈阳:东北大学, 2010. ZHOU Guangsen. Reasearch on the Profile Modification of the Involutes Gear[D]. Shenyang:Northeastern University, 2010. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10145-1013114730.htm |
 2015, Vol. 38
2015, Vol. 38

