b. 重庆大学 山地城镇建设与新技术教育部重点实验室,重庆 400045
b. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education
基于动力测试的损伤识别技术能够诊断结构出现的性能退化,便于对其进行维护和加固,从而预防出现结构倒塌等重大安全事故,故其已成为当前土木工程领域一个重要的研究方向[1]。从20世纪80年代起,国内外学者逐步提出了基于频域、时域、时频域的各种损伤识别方法[2-4],并在各类实验室结构中成功应用。但在实际结构中,损伤识别结果易受各种不确定性因素的影响,如荷载输入、测试误差、环境干扰等,导致结构损伤无法识别或多次识别结果出现相互矛盾的现象,这也是损伤识别方法在实际结构中较难应用的主要原因之一[5]。
概率原理、模糊理论和区间分析是目前解决不确定性问题的3种主要数学手段[6],其中,前两种手段计算结果的可靠性分别取决于概率密度函数或隶属度函数的精度。因土木结构尺寸巨大,难以进行做足尺模型的损伤实验,仅能获得结构健康状态的数据,因而获得的数据是片面的;同时,不同的结构在建造过程、使用环境和荷载作用等方面均存在差异,因此,从某个具体结构测试数据获取的规律往往无法直接用于其他结构。因此,当没有足够的数据来获得正确的概率密度函数或隶属度函数时,概率原理和模糊理论可能无法得出准确的结果[7]。
土木工程结构的物理参数、环境因素、荷载输入和响应等都具有明确的物理特性,仅能在一定范围内波动,如桥梁上的车辆荷载往往为1~120 t/辆,也就是说,这些因素将在一定区间内变化,且区间的上、下限可根据其物理意义直接确定。因此,基于区间分析的方法近年来逐步被引入土木工程领域,已用于结构静力分析、非概率可靠度、动力响应范围分析等方面[8-10]。
虽然区间分析有广阔的应用前景,但在损伤识别方面尚缺乏足够研究,且传统的区间求解算法易出现扩张问题,将其直接应用于损伤识别时,区间扩展易引发漏报警,从而使损伤识别失去作用。笔者采用向量自回归模型(VAR)主系数的马氏距离作为损伤识别特征指标,针对温度、环境激励、测试误差等不确定性影响因素,基于区间分析数学原理,引入粒子群算法提出区间优化求解方法,以克服区间扩展的难题,并提出区间重叠率判别指标和区间名义值距离指标,分别实现损伤部位和程度的识别。剪切型框架结构数值算例和实验室四层钢框架结构模拟结果表明,所提方法能正确识别不确定因素影响下的结构损伤,为受不确定因素影响下实际结构的损伤识别提供了技术支撑。
1 区间分析 1.1 区间分析原理实有界闭集
| $ \[\left\{ \begin{array}{*{35}{l}} a+b=\left[ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a},\bar{a} \right]+\left[ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b},\bar{b} \right]=\left[ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}+\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b},\bar{a}+\bar{b} \right]; \\ a-b=\left[ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a},\bar{a} \right]-\left[ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b},\bar{b} \right]=\left[ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}-\bar{b},\bar{a}-\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} \right]; \\ a\times b=\left[ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a},\bar{a} \right]\times \left[ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b},\bar{b} \right]= \\ \left[ \min \left( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}\times \underline{b},\bar{a}\times \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b},\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}\times \bar{b},\bar{a}\times \bar{b} \right), \right. \\ \left. \max \left( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}\times \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b},\bar{a}\times \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b},\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}\times \bar{b},\bar{a}\times \bar{b} \right) \right]; \\ a\div b=\left[ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a},\bar{a} \right]\div \left[ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b},\bar{a} \right]=\left[ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a},\bar{a} \right]\times \left[ \frac{1}{{\bar{b}}},\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}}} \right]。 \\ \end{array} \right.\] $ | (1) |
区间运算的交换律、结合律与实数的交换律、结合律不尽相同,更重要的是,区间基本运算将多次出现的同一变量视为相互独立的变量,这样将导致四则运算后的区间出现扩展现象。例如设a=[1, 2],则a-a=[1-2, 2-1]=[-1, 1],这与预期的a-a=[0, 0]并不相同。为克服区间扩展现象,不少学者提出了不同方法,常用的是区间组合法和区间截断法。
1.2 区间组合法如果函数f(x1, x2, …, xn)是区间变量xi(i=1, 2, …, n)的任一函数,那么函数f的区间变化范围可由变量xi的区间端点的组合来计算得到[11]。设
| $ {x_i} = \left[ {x_i^1,x_i^2} \right] = \left[ {{{\underline x }_i},{{\overline x }_i}} \right], $ | (2) |
式中,i=1, 2, …, n。则函数f取极值的所有可能组合为
| $ {f_{\rm{t}}} = f\left( {x_1^i,x_2^j, \cdots ,x_n^k} \right)。 $ | (3) |
其中,i, j, k=1, 2,t=1, 2, …, 2n,则函数f区间的上、下限值为所有极值中的最小值和最大值:
| $ f = \left[ {\underline f ,\overline f } \right] = \left[ {\min \left( {{f_{\rm{t}}}} \right),\max \left( {{f_{\rm{t}}}} \right)} \right]。 $ | (4) |
区间组合法仅对区间变量的上、下限值进行组合计算,因而能快速得到函数的区间,但当输入变量的个数较多时,其计算工作量将成指数倍增加。
1.3 区间截断法为了消弱区间扩张现象,文献[8]提出了区间截断法,其基本思路是采用变量区间的大小来缩减函数f的区间范围。
设函数区间变量a、b的函数为f(a, b),采用区间四则运算可得到函数f的上、下限分别为c、c,利用区间变量的名义值a0、b0可计算得到函数的名义值为c0。当c0远离0时,计算名义值c0距上、下限c、c的距离:
| $ {\Delta _1} = \left| {\frac{{\underline c - {c_0}}}{{{c_0}}}} \right|,{\Delta _2} = \left| {\frac{{\overline c - {c_0}}}{{{c_0}}}} \right|。 $ | (5) |
设t为区间变量a、b名义值与上、下限值的最大距离,则函数f的区间上、下限值可由t值截断得到:
| $ \left\{ \begin{array}{l} {\Delta _1} \le t,{\Delta _2} \le t,\underline f = \underline c ,\overline f = \overline c ;\\ {\Delta _1} > t,{\Delta _2} > t,\underline f = {c_0} + \left( {\underline c - {c_0}} \right),\overline f = {c_0} + t\left( {\overline c - {c_0}} \right);\\ {\Delta _1} \le t,{\Delta _2} > t,\underline f = \underline c ,\overline f = {c_0} + t\left( {\overline c - {c_0}} \right);\\ {\Delta _1} > t,{\Delta _2} \le t,\underline f = {c_0} + t\left( {\underline c - {c_0}} \right),\overline f = \overline c 。 \end{array} \right. $ | (6) |
由式(6)可知,截断法采用变量上、下限值与名义值的最大距离t来限制函数f上、下限可能出现的扩展。
1.4 基于粒子群的区间优化求解法传统的区间分析方法易出现区间扩展现象,而优化算法为克服该问题提供了方法选择。从优化方法的角度来看,在区间变量的变化范围内,求函数f的区间上、下限值就是在区间变量范围内,求函数的最大、最小值:
| $ \left\{ \begin{array}{l} \max f\left( {{x_1}, \cdots ,{x_n}} \right)and\;\min f\left( {{x_1}, \cdots ,{x_n}} \right),\\ {\rm{s}}{\rm{.t}}{\rm{.}}{\underline x _i} \le {x_i} \le {\overline x _i}。 \end{array} \right. $ | (7) |
因此,函数区间上、下限值的求解可以转化为优化问题进行计算,选取粒子群优化算法(particle swarm optimization, PSO)。粒子群算法的基本思路是模拟鸟群的觅食行为,通过在解空间内不断迭代寻优从而得到最优解[12-13]。首先,在解空间内初始化一组粒子zi={z1i, z2i, …, zni }(i=1, 2, …, m),其中n为区间变量的个数,m为粒子的个数。计算函数f的值,对求解下限值问题,记当前迭代步函数最小值所对应的粒子为pbest,从开始到当前迭代步函数最小值所对应的粒子为gbest,则第i个粒子下一个迭代步更新的策略为
| $ \left\{ \begin{array}{l} {v_i} = w \times {z_i} + {c_1} \times rand \times \left( {{p_{{\rm{best}}}} - {z_i}} \right) + {c_2} \times rand \times \left( {{g_{{\rm{best}}}} - {z_i}} \right),\\ {z_i} = {z_i} + {v_i}; \end{array} \right. $ | (8) |
式中:w为权重;c1、c2为学习因子;rand为[0, 1]之间的随机数。从公式(8)可知,粒子更新由3部分决定:一是粒子先前的速度,起到了平衡全局和局部搜索能力的作用;二是认知部分,即对自身的学习,保证了粒子群算法的全局搜索能力;三是社会部分,即对群体内最优个体的学习,体现了粒子间的信息共享。粒子群算法迭代终止的方法较多,选取固定迭代次数法,即迭代30次后终止粒子群算法,给出最终结果。
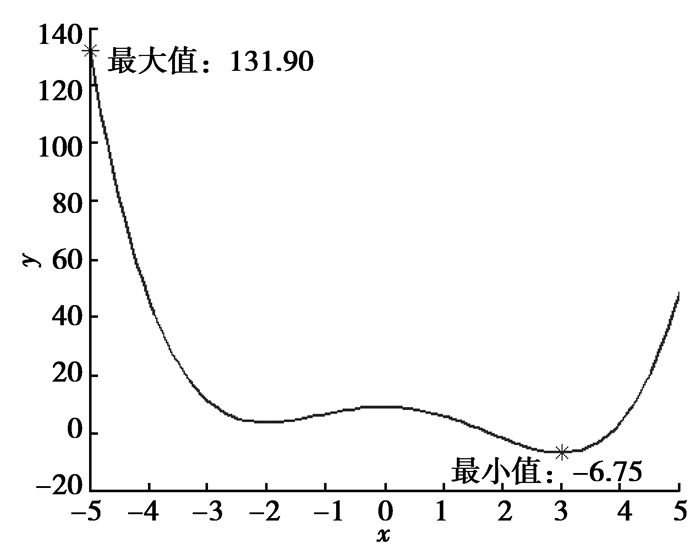
1.5 3种区间求解方法的对比为便于对比,取数值函数y=x4/4-x3/3-3x2+9为例,其中,x∈[-5, 5],该数值函数的理论变化区间为y∈[-6.75, 131.90],如图 1所示。
|
图 1 函数变化区间 Figure 1 The interval of the function |
采用区间组合法运算得到的函数区间y1∈ [-241.12, 257.63];采用区间截断法计算的函数区间y2∈[9.00, 131.90];取粒子种群数为30,计算得到函数的区间y3∈[-6.75, 131.90]。
从3种求解方法的计算结果可知,因区间变量x在函数中的重复次数较多,区间组合法计算的上、下限值远远大于理论值,出现了明显的区间扩展现象;区间叠加法能在一定程度上减弱区间扩展现象,如所求的区间上限回到了真实值,但其通过变量的区间范围来截断函数变化的区间范围,可能会过小限制函数区间的变化,从而未得到真实的函数区间下限值;虽然基于PSO的优化求解算法的计算效率不如前两种方法,但其能够正确求解函数的区间上、下限值,所得的结果更为精确。
2 基于区间分析的不确定性损伤识别 2.1 损伤特征指标提取为便于实现在线损伤识别,选取基于数据驱动的方法建立损伤特征指标。向量自回归模型(vector auto-regression, VAR)是一种用于描述多个不同变量之间内在联系的模型,一个p阶的VAR模型[14]可表述为
| $ {y_t} = \mathit{\boldsymbol{c + }}{\mathit{\boldsymbol{A}}_1}{y_{t - 1}} + \cdots + {\mathit{\boldsymbol{A}}_p}{y_{t - p}} + {e_t}, $ | (9) |
式中:Ai为n×n的系数矩阵,n为变量的个数;et为误差项;c为插值向量,损伤识别中,数据通常会进行零均值归一化处理,故该项为零,可省略;下标t表示时间步。
通过文献[14]的理论推导表明,当采用结构位移差分来表示速度和加速度时,结构运动方程可写成类似VAR模型的形式,则VAR模型系数矩阵与土木工程结构动力运动方程的刚度、阻尼矩阵具有对应关系,故可采用VAR模型系数项的变化来识别损伤。取所有系数项对角线元素组成向量h:
| $ \mathit{\boldsymbol{h}} = {\left\{ {A_1^{11},A_1^{22}, \cdots ,A_1^{nn},A_2^{11}{\rm{,}} \cdots {\rm{,}}A_2^{nn}, \cdots A_p^{11}, \cdots A_P^{nn}} \right\}^{\rm{T}}}. $ | (10) |
向量h为n×p的高维向量,不便于作为损伤指标进行分析计算,故采用马氏距离(MD)将其降维,从而建立损伤特征指标M:
| $ M\left( h \right) = \sqrt {{{\left( {h - h{{\hat h}_b}} \right)}^{\rm{T}}}S_b^{ - 1}\left( {h - h{{\hat h}_b}} \right),} $ | (11) |
式中:ĥb为基准状态下向量h的平均值;Sb-1为基准状态下向量h的协方差。
2.2 基于区间分析的损伤识别方法在结构健康以及未知状态下进行少量测试,结合区间优化求解方法和损伤特征指标算法,将健康和未知状态下损伤特征指标的区间分别表示为
|
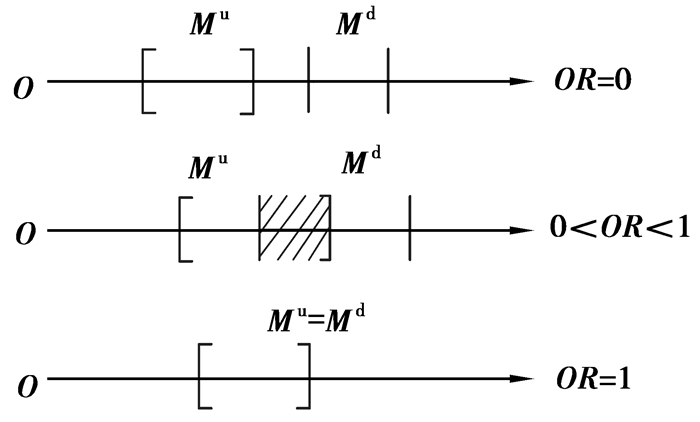
图 2 结构不同状态下区间重叠率的示意图 Figure 2 The overlapping rate under different conditions |
从图 2可知,当Mu和Md的区间完全分离时,可以严格地判定结构损伤;当Mu和Md的区间完全重叠时,可以严格地判定结构未发生损伤,但当Mu和Md的区间部分重叠时,则较难直接给出结构损伤的判定,此时,定义Mu和Md的区间重叠率为
| $ OR = \left( {{{\bar M}^{\rm{u}}} - {{\underline M }^{\rm{d}}}} \right)/\left( {{{\bar M}^{\rm{d}}} - {{\underline M }^{\rm{u}}}} \right)。 $ | (12) |
当健康和损伤状态的区间名义值分别与损伤状态的下限值、健康状态的上限值重叠时,OR=1/3。当OR进一步增大时,健康状态的名义值将被包含在损伤状态区间内,因名义值在概念上类似于平均值,当其被包含在另一状态区间时,将很难区分结构是否发生损伤,因此,笔者建议取OR=0.3作为结构损伤的判定阈值,即当OR≤0.3时,判定结构出现损伤。当OR < 0时,取OR=0。
随着损伤程度的增加,Mb和Md区间将由重叠变为分离,并且分离的距离将逐渐增加。因此,当判别某个部位出现损伤后,采用Mb和Md区间名义值之间的距离作为名义值距离指标,采用该指标来判断结构损伤的程度。
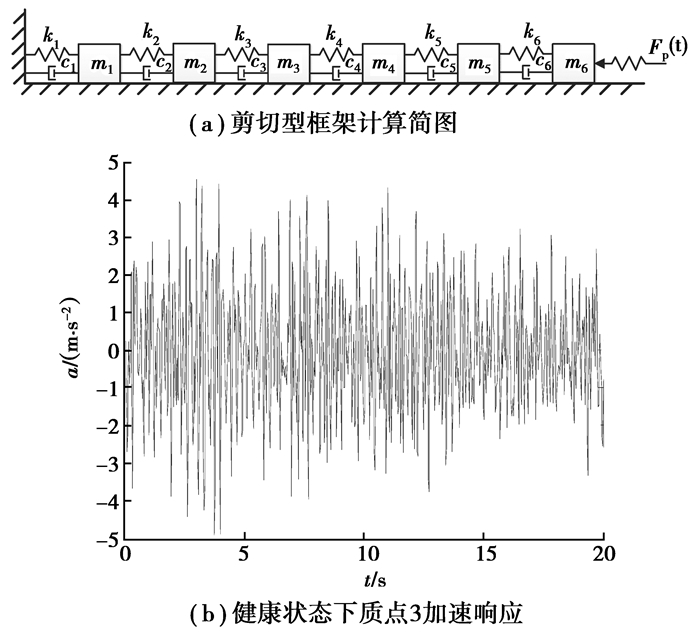
3 框架结构算例分析 3.1 数值算例取图 3所示的6自由度集中质量弹簧模型作为剪切型框架结构的简化模型,其中,各质量取为m1=m2=1,m3=m4=0.8,m5=m6=0.5;各弹簧的刚度取值为k1=k6=1 500,k2=k3=1 200,m4=m5=1 000。体系的阻尼设为瑞雷比例阻尼,即
| 表 1 损伤工况 Table 1 Damage cases |
|
图 3 模型简图和质点加速度响应 Figure 3 Simplified model and acceleration response of mass |
假设由于不确定因素的影响,k1、k2和k3均在其名义值10%以内的范围内波动,例如k1∈[1 350, 1 650],且在计算加速度中加入5%的白噪声来模拟由测试误差带来的不确定性。
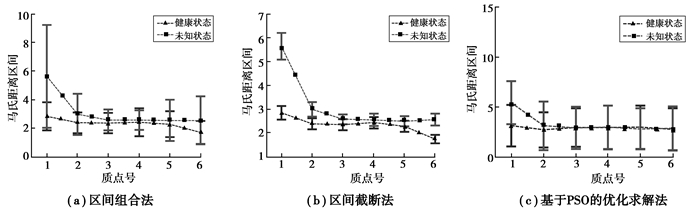
在健康状态和损伤工况下,采用AIC准则确定VAR模型的阶次p[14],建立VAR模型,然后分别计算得到健康状态和待检状态下的马氏距离。通过多次计算健康状态和损伤工况下6自由度的加速度响应并提取相应的马氏距离区间。采用区间组合法、区间截断法和基于PSO的优化求解法,共3种方法在损伤工况1下计算得到的马氏距离MD的区间如图 4所示。
|
图 4 工况1下3种算法的马氏距离区间 Figure 4 The interval of MD under damage case 1 |
由图 4可知,除区间截断法在质点1、6处马氏距离完全分开外,其余测点及另外两种方法各测点处的马氏距离均重现重叠状态,故进一步采用公式(12)的定义计算OR指标如表 2所示。
| 表 2 损伤工况1下的OR指标 Table 2 OR under damage case 1 |
在表 2中,将小于0.3的值用粗体标出,表示其对应的质点处有较大可能出现损伤。从表 2可以看出,区间截断法在质点1、2、6处的值均小于0.3,而真实的损伤仅发生在质点1处,因此,区间截断法出现了误判。虽然区间组合法和本文采用的基于PSO的优化方法均能正确识别结构的损伤部位。对于未出现损伤的质点2至质点6处,区间组合法和本文方法所得OR指标的平均值分别为0.67和0.97。OR值越接近1,表明损伤判定的可信度也越低,因此,本文方法在未损伤的质点2至质点6处得出结构为健康状态的可信度更高。
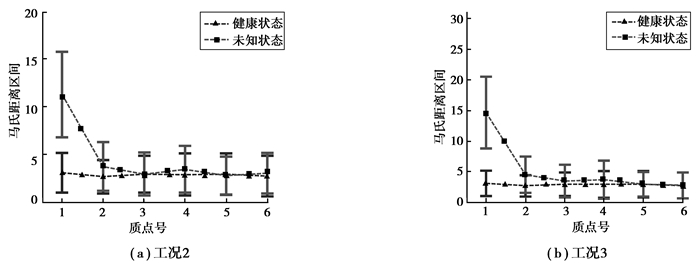
采用本文方法计算工况2和工况3下的马氏距离区间如图 5所示,各质点处的OR指标如表 3所示。
| 表 3 损伤工况1下的OR指标 Table 3 OR under damage case 1 |
|
图 5 工况2和工况3下本文方法计算的马氏距离区间 Figure 5 The interval of MD using the PSO optimal algorithm under damage case 2 and 3 |
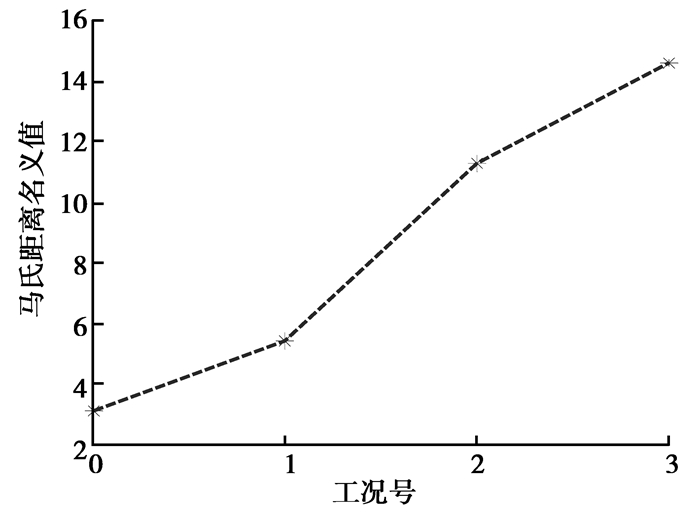
从图 5和表 3可以得出,即使在不确定因素影响下,基于PSO的区分分析方法能正确识别结构损伤的部位。将3种工况下马氏距离区间的名义值距离绘制于图 6中。
|
图 6 马氏距离区间的名义值距离 Figure 6 The distance of nominal value of MD |
在图 6中,区间名义值的距离随着损伤的增大而逐步增大,表明采用该指标可以准确识别出结构损伤的相对程度。
3.2 框架模型试验采用尺寸为350 mm×65 mm×4 mm的钢板作为梁和柱,在实验室搭建四层单跨钢框架结构,各钢板之间用节点板和螺栓连接,底层柱与刚性底座通过螺栓固定,如图 7(a)所示。通过更换截面减小的柱来模拟结构的损伤,如图 7(b)所示。分别将第二层的两根柱子截面分别减少10%、20%、30%和40%共4种损伤工况,并分别记为工况1至工况4。应说明的是,图 7(b)中仅给出了一根柱子的3种不同损伤工况。

|
图 7 四层钢框架及测试的加速度响应 Figure 7 Experimental set-up and acceleration response |
采用KDJ-50型电磁激振器在第一层右柱的中部对结构施加白噪声激励。4个加速度传感器分别布设在各层梁处,从下至上分别记为传感器1至传感器4。
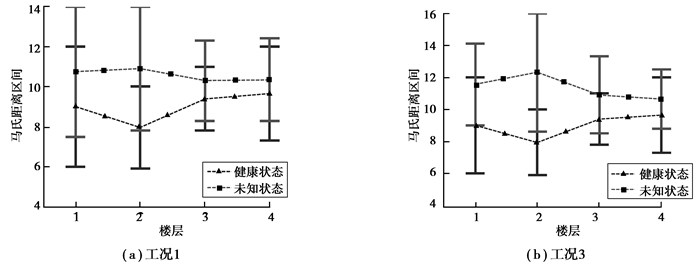
在各个损伤工况下,分别在1层至4层梁上增加100、200、300 g的磁铁,以模拟实际结构不同时刻人群荷载等物理参数的波动。计算得到的马氏距离区间如图 8所示,OR指标如表 4所示。
| 表 4 试验结构的OR指标 Table 4 OR of the tested structure |
|
图 8 部分损伤工况下的马氏距离区间 Figure 8 The interval of MD under partial damage cases |
从图 8和表 4可知,对于试验框架,基于区间分析的损伤识别方法能成功实现损伤定位。应指出的是,随着损伤的增大,其余各楼层处测点的OR值也逐渐降低,例如在工况4下,楼层1测点的OR值已接近0.3,这主要是因为随着损伤的增大,损伤将引起更多部位的响应发生明显改变。
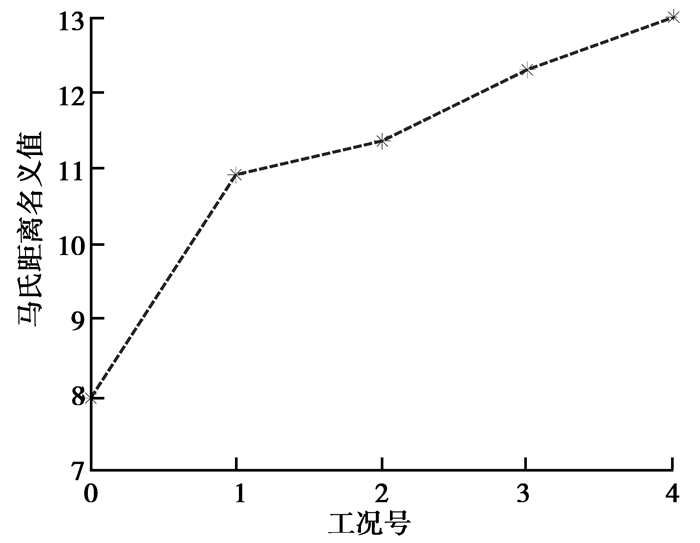
计算各工况下的马氏距离区间的名义值如图 9所示。由该图可知,采用区间名义值距离指标能准确识别出结构的损伤程度。
|
图 9 马氏距离区间的名义值 Figure 9 The nominal value of MD |
针对土木工程结构易受荷载、环境温度、测试噪声等不确定性因素影响,且测试数据量少、测试数据较为片面的实际情况,提出了基于区间分析的非概率不确定性损伤识别方法。将不确定影响因素引起损伤特征指标的波动采用区间表示,建立了区间优化求解方法,在此基础上,提出了根据区间重叠率指标和区间名义值距离指标分别进行损伤定位和损伤程度识别的方法。通过数值算例和试验模型的试验表明,所提方法能应用于不确定因素影响下的损伤识别。同时,笔者采用的数值模拟和试验结构均较简单,与大型复杂土木结构工程实际运用环境下遭遇的不确定因素仍有较大差异,将该方法应用于这些大型结构是下一步需重点开展的工作。
| [1] |
任松, 王新胜, 姜德义, 等.
隧道长期安全监测及评价模型[J]. 重庆大学学报, 2009, 32(11): 1345–1351.
REN Song, WANG Xinsheng, JIANG Deyi, et al. Monitoring and evaluation model of tunnel long-term safety[J]. Journal of Chongqing University, 2009, 32(11): 1345–1351. (in Chinese) |
| [2] | Kammer D C. Test-analysis model development using an exact modal reduction[J]. International Journal of Analytical and Experimental Modal Analysis, 1987, 2(4): 174–179. |
| [3] | Pandey A K, Biswas M. Damage detection in structures using changes in flexibility[J]. Journal of sound and vibration, 1994, 169(1): 3–17. DOI:10.1006/jsvi.1994.1002 |
| [4] | Levin R I, Lieven N A J. Dynamic finite element model updating using neural networks[J]. Journal of Sound and Vibration, 1998, 210(5): 593–607. DOI:10.1006/jsvi.1997.1364 |
| [5] | Ben-Haim Y. A non-probabilistic concept of reliability[J]. Structural Safety, 1994, 14(4): 227–245. DOI:10.1016/0167-4730(94)90013-2 |
| [6] | Ben-Haim Y. A non-probabilistic measure of reliability of linear systems based on expansion of convex models[J]. Structural Safety, 1995, 17(2): 91–109. DOI:10.1016/0167-4730(95)00004-N |
| [6] |
孙彬, 牛荻涛, 王庆霖.
基于区间分析的锈蚀钢筋混凝土结构使用寿命预测[J]. 建筑结构学报, 2012, 33(6): 110–115.
SUN Bin, NIU Ditao, WANG Qinglin. Service life prediction of corroded RC structures based on interval analysis[J]. Journal of Building Structures, 2012, 33(6): 110–115. (in Chinese) |
| [7] | Simoen E, Moaveni B, Conte J P, et al. Uncertainty Quantification in the Assessment of Progressive Damage in a 7-Story Full-Scale Building Slice[J]. Journal of Engineering Mechanics, 2013(12): 1818–1830. |
| [8] | Rao S S, Berke L. Analysis of Uncertain Structural Systems Using Interval Analysis[J]. AIAA Journal, 1997, 35(4): 727–735. DOI:10.2514/2.164 |
| [9] | Simoen E, Roeck G D, Lombaert G. Dealing with uncertainty in model updating for damage assessment: A review[J]. Mechanical Systems and Signal Processing, 2015(56/57): 123–149. |
| [10] | Alefeld G, Mayer G. Interval analysis: theory and applications[J]. Journal of Computational and Applied Mathematics, 2000, 121(1/2): 421–464. |
| [11] | Moore R E, Kearfott R B, Cloud M J. Introduction to Interval Analysis[J]. Society for Industrial and Applied Mathematics, 2009(269): 201–223. |
| [12] |
陈进, 汪泉, 李松林, 等.
改进的粒子群算法在翼型优化设计中的应用[J]. 重庆大学学报, 2012, 35(11): 40–46.
CHEN Jin, WANG Quan, LI Songlin, et al. Airfoil design using improved particle swarm optimization[J]. Journal of Chongqing University, 2012, 35(11): 40–46. (in Chinese) |
| [13] |
毛玉星, 韩倍涛, 冯莲, 等.
粒子群优化算法实现仿射不变性形状识别[J]. 重庆大学学报, 2010, 33(3): 65–71.
MAO Yuxing, HAN Beitao, FENG Lian, et al. Affine invariant shape recognition with particle swarm optimization algorithm[J]. Journal of Chongqing University, 2010, 33(3): 65–71. (in Chinese) |
| [14] | HUANG Z M, LIU G, Todd M, et al. Damage detection using vector auto-regressive models[J]. Health Monitoring of Structural and Biological Systems, 2013, 8695(1): 117–136. |
 2015, Vol. 38
2015, Vol. 38


