2. 福州大学 土木工程学院,福州 350108
2. College of Civil Engineering, Fuzhou University, Fuzhou 350108, P.R.China
在地震发生条件下供水管网络中若某一环节出现破坏,都有可能引起整个供水网络的功能丧失,影响到整个城市生命线系统正常运行,直接影响灾后的社会生活秩序和社会生产建设[1]。如何正确分析和评估震后供水系统连通运行状态,对城市震后救灾和及时修复具有重要的意义,也是提高供水管网性能和进行震后管网加固优化设计所亟待解决的问题。
国内外学者对震后供水管网的连通性做了较多研究。Benamin等最早用概率法分析供水网络的可靠度。Wanger等[2]采用概率方法分析串并联系统及一般网络系统的可达性和连通性,对满足供水需求的管网进行了连通可靠性分析。刘锡荟等[3]以概率统计、模糊数学为基础建立管网震害预测模型,通过Monte Carlo模拟和不精确性推理进行管网可靠度分析,并应用于城市供水管网震害预测。金国梁[4]采用BFS算法结合蒙特卡罗模拟技术判断城市给水管网的连通可靠性。刘威等[5]基于模糊随机性,以代数方程求解和通过仿真映射技术预测网络震害。王杨等[6]基于Monte Carlo法和广度搜索算法,对管网系统模拟原有参数并对系统网络进行分析。Yang等[7]提出区域供水管网连通可靠性分析的最小割集方法,采用网络流量模型(EMNET)确定最优系统运算,根据分析结果确定关键路径,并结合实例进行可靠性分析。李听[8]基于BP神经网络模型建立管道单体地震反应分析模型和管网系统连通性预测模型,评估供水管网震后运行状态。韩阳等[9]利用GO法进行供水管网可靠度的计算,并通过matlab语言进行求解算法程序编制从而求解供水管网可靠度。何双华[10]通过Monte Carlo随机模拟过程结合模糊关系矩阵法分析连通可靠性。上述方法中采用模拟管网的震后运行状态工作量大,仅从管道单元或从管网单一角度分析连通性,而未从管道单元和考虑整个管网权向角度分析连通性。因些,文中对震后供水管网的连通可靠性分析方法进行了改进,在管道单体震害预测基础上,采用基于神经网络的Monte Carlo和图论法,通过模拟再现管网中各管线的破坏情况,分析各管网单元可靠性及判断整个管网的可靠度。
1 管道单体的震害预测供水管道单元在地震的作用下破坏数值存在随机性,其破坏状态分为:基本完好、中等破坏和严重破坏[11]。得到的功能函数为
| $ Z = f\left( {R, S} \right) = R-S. $ | (1) |
作为结构功能函数的基本变量,以管道接口在地震波作用下的变形S、接头允许变形R,用容许开裂变形极限抗力R1和容许渗漏变形极限抗力R2来表示。假定条件如下:处于基本完好与中等破坏的临界状态:Z1=R1-S;处于中等与严重破坏的临界状态:Z2=R2 -S。管道3种状态为:当Z1>0时,基本完好状态;当Z2<0时,严重破坏状态;当Z1<0∩Z2>0时,中等破坏状态。
在地震作用下,管道变形概率的变量若服从正态分布时,用极值公式计算。当随机变量为非正态分布时,需对其当量正态变换计算失效概率。即在设计验算点x*处,令原分布函数F(x)和当量正态随机变量的分布函数一致,求出相应正态分布的标准差σN和均值μN。
| $ {\sigma ^N} = \varphi \{ {\mathit{\Phi }^{- 1}}[F({x^ * })]\} /f({x^ * }), $ | (2) |
| $ {\mu ^N} = {x^*}- \mathit{\Phi }[F({x^*})]{\sigma ^N}, $ | (3) |
式中:Φ-1(·)是标准正态分布函数的反函数;φ(·)是标准正态分布的概率密度函数。
随机变量S服从极值Ⅰ型分布,设其均值和标准差分别为μ和σ,则其概率密度函数和分布函数分别为[12-13]:
| $ f(x) = {\alpha ^{[-a\left( {x-u} \right)-e - a\left( {x - u} \right)]}}, $ | (4) |
| $ F\left( x \right) = {{\rm{e}}^{-{\rm{e}}-a\left( {x-u} \right)}}, $ | (5) |
其中,参数α和u由下式求得:
| $ a = \frac{{1.282\;5}}{\sigma }, \;\;u = \mu-\frac{{0.577\;2}}{a}。 $ |
将式(4)和式(5)分别代入式(2)和式(3),可得到变量方差和均值。
2 基于神经网络的Monte Carol法供水管网连通可靠性分析 2.1 管线破坏概率的确定供水管网中由各相邻节点连结形成各管道单元及由此串联而成,基本完好的概率P1、中等破坏的概率P2和严重破坏的概率P3 [14]。管线震害程度综合评价分为:当P1≥0.6时,管线处于基本完好状态;当P1<0.6∩P3<0.25时,管线处于中等破坏状态;当P3≥0.25时,管线处于严重破坏状态[15]。
2.2 基于神经网络的Monte Carol法分析管段连通性用神经网络的Monte Carol法评价供水管网系统的可靠性,拟再现管网各边的破坏状态,以各汇点不连通频率作为近似值评价管网的连通可靠性[16-17]。其步骤如下:
1)以{xi,Z(xi)}(i=1, 2, …, s)作为输入数据,设计神经网络结构,输出层以Z(xi)函数输入层个数,X的维数n作为单元数。
2)随机抽样得xi(i=1, 2, …, N),利用数据{xi,Z(xi)}(i=1, 2, …, s)训练网络。
3)用已训练网络模拟计算Z(xi)(i=1, 2, …, N),采用式
以供水管的节点以及连各节点的边所组成网络图,以管线的破坏概率作为权,将有向加权图代表供水管网流向,其步骤如下:
1)采用基于神经网络的Monte Carlo法进行管网模拟,比较其失效概率与其破坏概率pij,所得节点邻接矩阵A,
| $ a\left\{ \begin{array}{l} 1, {r_{ij}} \le {p_{ij}}\\ 0, {r_{ij}} > {p_{ij}}。 \end{array} \right. $ |
2)计算An-1,n为节点总数,并求M=I+A1+A2+A3+…+An-1,由mij值判断节点i、j之间连通性(若mij=0,不连通;若mij≥1,连通);
3)按式(2)进行多次模拟,每次模拟结果形成连接矩阵T,
4)重复以上三步骤,模拟5 500次,各节点连通频率由连通概率近似值确定。
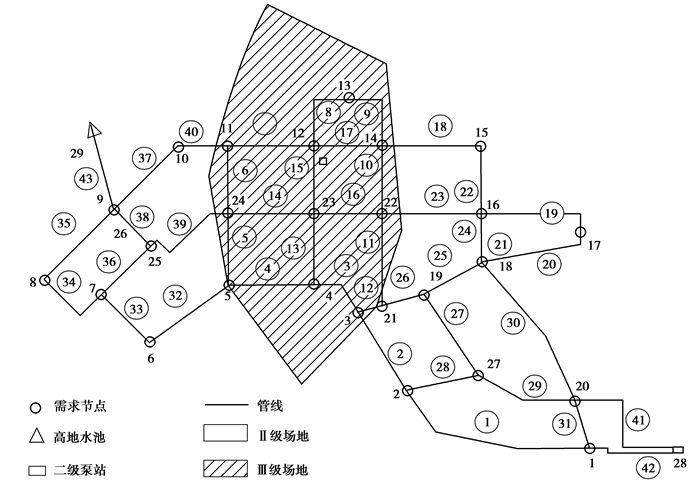
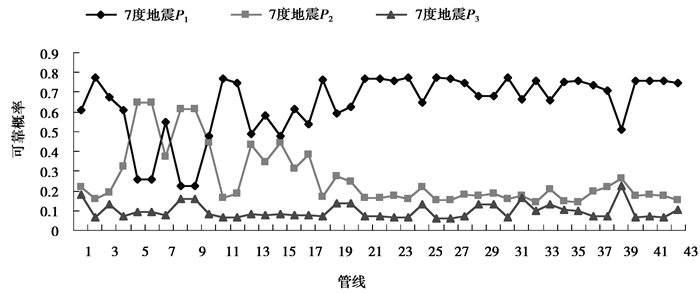
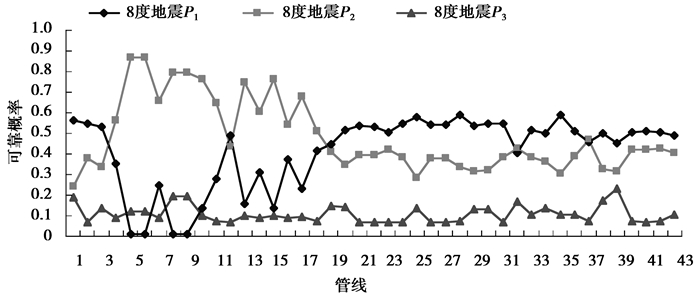
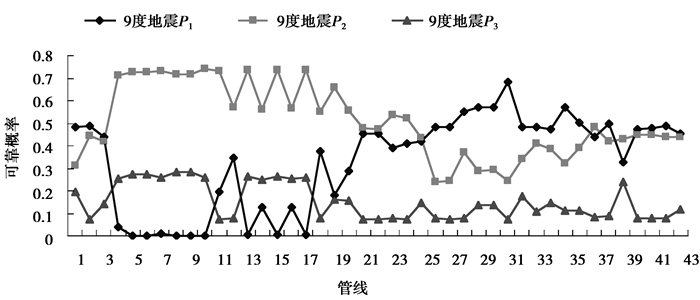
3 实例分析供水管网实例如图 1所示,在7、8、9级地震烈度条件下,计算各管线可靠性概率和评价管线震害状态,结果如图 2、图 3和图 4所示。
|
图 1 城市供水管网的平面图及所处Ⅱ、Ⅲ场地条件 Figure 1 The plan view of the ground condition and pipe network of the calculation example |
|
图 2 7度地震作用下各管线的可靠度 Figure 2 The pipeline reliability at earthquake intensity Ⅶ |
|
图 3 8度地震作用下各管线的可靠度 Figure 3 The pipeline reliability at earthquake intensity Ⅷ |
|
图 4 9度地震作用下各管线的可靠度 Figure 4 The pipeline reliability at earthquake intensity Ⅸ |
依据管线破坏概率的破坏原则确定[5-6],在7度、8度、9度地震作用下,各管线所受损害程度情况如表 1所示。在7度地震作用下,大部分管线处于基本完好状态,中等破坏状态有16段管线。在8度地震作用下,所有管线已经处在中等破坏状态。在9度地震作用下,10段管线处严重破坏状态,其他各管均处在中等破坏状态。从破坏管段所处位置来看,在地震作用下处于三类场地的管段所受到震害破坏比处于二类场地管段相对严重。
| 表 1 各管线在不同地震作用下所受损害程度 Table 1 Seismic damage of the pipeline at earthquake intensity |
在地震烈度为7度、8度、9度条件下,采用基于神经网络的Monte Carlo法和图论法对实例进行5 500次模拟,各节点连通情况如图 3所示。
|
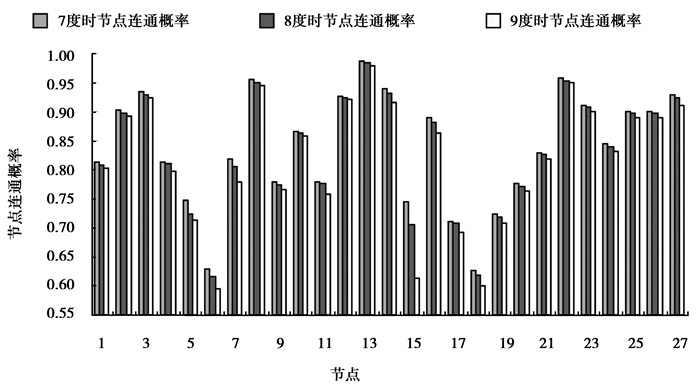
图 5 在不同地震作用下1~27节点连通概率 Figure 5 1~27 nodes connected probability at earthquake intensity |
从连通概率结果来看,地震烈度在7度、8度、9度条件下,管网中各节点的连通概率伴随地震烈度增大而降低。其中,节点15伴随地震烈度增大同时连续概率变化最为显著,原因在于该节点处于Ⅲ类场地,且离水源点又远。
4 结语利用基于神经网络的蒙特卡方法进行管网模拟,并结合图论方法应用于各管网节点和各管段的连通可靠性分析,判断整个城市供水管网抗震可靠性。结合实例分析表明,该方法能有效判断管网在地震条件下的连通可靠性,以及随地震烈度逐渐增大同时管网受到的破坏程度逐渐加重。从实例分析结果来看,此方法是可行和合理的,为城市地下管线防灾减灾管理提供借鉴。
| [1] |
牛志广, 高希丽, 王晨晨.
城市供水管网脆弱性评价研究进展[J]. 中国安全科学学报, 2012, 22(6): 157–163.
NIU Zhiguang, GUO Xili, WANG Chenchen. A review of vulnerability assessment of urban water supply network[J]. China Safety Science Journal, 2012, 22(6): 157–163. (in Chinese) |
| [2] | Wagner J M, Shamir U, Marks D H. Water distribution reliability: analytical methods[J]. Journal of Water Resources Planning and Management, 1988, 4(3): 253–275. |
| [3] |
刘锡荟, 李鹏程, 张锐.
城市生命线工程抗震的模糊图分析方法[J]. 地震工程与工程振动, 1989, 9(1): 35–46.
LIU Xihui, LI Pengcheng, ZHANG Rui. The fuzzy graph analysis method of urban lifeline engineering Seismic reliability[J]. Earthquake Engineering and Engineering Vibration, 1989, 9(1): 35–46. (in Chinese) |
| [4] |
金国梁.
生命线工程网络震害预测方法讨论[J]. 工程抗震, 1994(4): 32–36.
JIN Guoliang. Lifeline engineering network seismic damage prediction method discussion[J]. Journal of Engineering Seismic, 1994(4): 32–36. (in Chinese) |
| [5] |
刘威, 李斌, 李杰.
供水管网渗漏模型研究[J]. 地震工程与工程振动, 2014, 34(1): 180–186.
LIU Wei, LI Bin, LI Jie. Leakage model of water distribution network[J]. Earthquake Engineering and Engineering Vibration, 2014, 34(1): 180–186. (in Chinese) |
| [6] |
王杨, 邬瑞峰, 侯忠臣.Monte Carlo法分析地下管网系统在地震作用下的服务能力[C].地下管线抗震-计算方法与工程应用.冶金工业部建筑研究总院防灾抗震工程研究所, 1991:61-65. WANG Yang, WU Ruifeng, HOU Zhongchen. The action of service ability of the underground pipe network system in the earthquake by Monte Carlo method analysis [C]. Underground pipeline seismic-calculation method and engineering application, Disaster prevention seismic engineering research institute of metallurgical industry ministry building research institute, 1991:61-65. (in Chinese) |
| [7] | Yang S L, Hsu N S, Louie P W F, et al. Water distribution network reliability: connectivity analysis[J]. Journal of Infrastructure Systems, 1996, 2(2): 54–64. DOI:10.1061/(ASCE)1076-0342(1996)2:2(54) |
| [8] |
赵新华, 陈春芳, 郑毅.
给水管网可靠度的计算[J]. 中国给水排水, 2000, 16(1): 57–60.
ZHAO Xinhua, CHEN Chunfang, ZHENG Yi. Calculation of Water Supply Network Reliability[J]. China Water and Wastewater, 2000, 16(1): 57–60. (in Chinese) |
| [9] |
韩阳, 刘宏奎.
生命线网络可靠性分析的类分法[J]. 地震工程与工程振动, 2002, 22(2): 49–53.
HAN Yang, LIU Hongkui. A topological classification method for lifeline risk analysis[J]. Earthquake Engineering and Engineering Vibration, 2002, 22(2): 49–53. (in Chinese) |
| [10] |
何双华, 赵洋, 宋灿.
城市供水管网在地震时的连通可靠性分析[J]. 防灾减灾工程学报, 2011, 31(5): 587–589.
HE Shuanghua, ZHAO Yang, SONG Can. Seismic connectivity reliability analysis of urban water supply network[J]. Journal of Disaster Prevention and Mitigation Engineering, 2011, 31(5): 587–589. (in Chinese) |
| [11] |
陈玲俐, 李杰.
城市供水管网系统抗震功能可靠度分析[J]. 工程力学, 2004, 21(4): 45–50.
CHEN Lingli, LI Jie. Aseismatic service ability analysis of water supply network[J]. Engineering Mechanics, 2004, 21(4): 45–50. (in Chinese) |
| [12] |
李杰. 生命线工程抗震--基础理论与应用[M]. 北京: 科学出版社, 2005: 68-75.
LI Jie. Aseismatic Basic Theory and Application of Lifeline[M]. Beijing: Science Press, 2005: 68-75. (in Chinese) |
| [13] | Ang W K, Jowitt P W. Solution for water distribution system under pressure-deficient conditions[J]. Water Resources Planning and Management, 2006, 132(3): 175–182. DOI:10.1061/(ASCE)0733-9496(2006)132:3(175) |
| [14] | Han Y, Sun S P.Seismic reliability of lifeline systems[C]. Earthquake Engineering Frontiers in the New Millennium, Lisse: Swets and Zeitlinger, 2001:209-213. |
| [15] |
杜坤, 龙天渝, 郭劲松, 等.
地震导致渗漏的供水管网水力模拟[J]. 土木建筑与环境工程, 2013, 35(3): 126–130.
DU Kun, LONG Tianyu, GUO Jinsong, et al. Simulation for leaky water distribution system caused by earthquake[J]. Journal of Civil Architectural and Environmental Engineering, 2013, 35(3): 126–130. (in Chinese) |
| [16] |
张明. 结构可靠度分析[M]. 北京: 科学出版社, 2008: 23-35.
ZHANG Ming. Structure reliability analysis[M]. Beijing: Science Press, 2008: 23-35. (in Chinese) |
| [17] |
符圣聪, 江静贝, 黄世敏.
地震时供水管网的可靠性和功能分析(下)[J]. 工程抗震与加固改造, 2007, 29(2): 95–99.
FU Shengcong, JIANG Jingbei, HUANG Shimin. Reliability and function analysis of water supply networks post-earthquake[J]. Earthquake Resistant Engineering and Retrofitting, 2007, 29(2): 95–99. (in Chinese) |
 2015, Vol. 38
2015, Vol. 38

