1 机器鱼的设计 1.1 多关节机器鱼模型

对于鳇科鱼类的游动，前2/3的鱼身动作在很大程度上是刚性的方式，有推进力的部分仅限于鱼身后部的1/3。尾部是由一个细长的通常可以忽略流体动力影响的柄与鱼身相连。

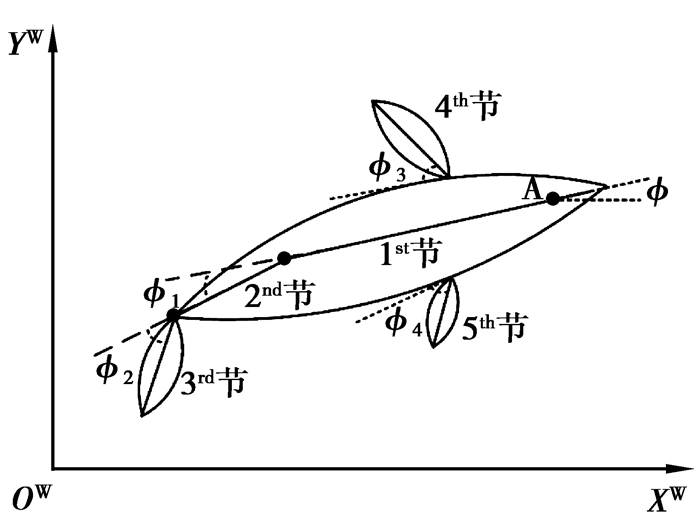
如图 1所示，鳇科鱼可以建模为多关节模型。鱼的主体被模拟成2个刚性部件连接在一起。尾部和鳍片可以被看做刚性的升力面，它们按照流体力学的原理通过摆动和升降运动来产生推力。X^wO^wY^w为全局坐标系。整个身体的位置和方向通过x^w, y^w, 和ϕ₃个坐标来描述。x^w和y^w表示位于1/8体长处的点A的位置(鱼2只眼睛的中点)，而ϕ表示X轴到1^st连接的夹角。整个鱼身在全局坐标系上的运动可以被描述为fm(x^w, y^w, ϕ, t)。ϕ_i(i=1, 2, 3, 4)表示实际控制的角度，即相邻的连线之间的关节角。

机器鱼游动的推力由鱼身的弯曲、鱼鳍的起伏以及鱼尾的摆动产生，因此可以通过操纵ϕ_i(t)来控制鱼的“形”而产生运动。因此，存在一个关节角位移ϕ_i(t)与游泳模式之间的关系或映射。然而，这样的映射很难被明确地写出，因为精确的鱼类运动流体力学原理是未知的，而且许多基本鱼类游动的运动学是与力学相结合的。笔者通过一个新颖的仿生学习机制来探讨这个映射。

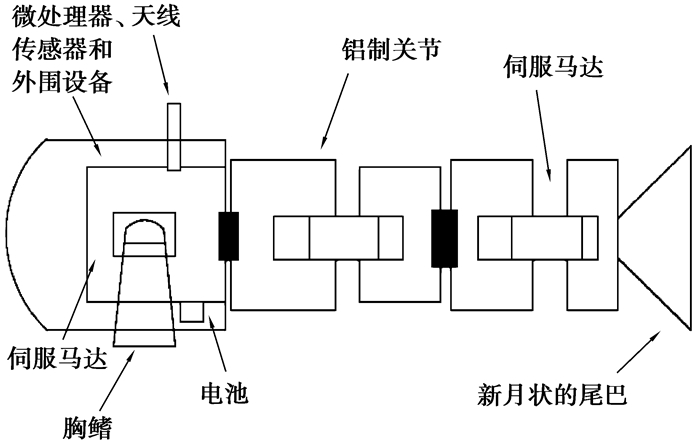
1.2 多关节机器鱼机械结构

笔者设计的机器鱼如图 2所示。机器鱼大约长30 cm，包括2个伺服舵机，一个微处理器，一个无线通信模块，5个铝制连接件，一组传感器，以及一些外围设备。2个用于控制机器鱼身体段运动的舵机和鱼尾串联在一起充当鱼体运动的推进器。微处理器(AVR Mega32)用来对传感器数据以及无线信号进行分析和处理，并根据内在的规则作出决策，控制机器鱼的运动。

2 鱼游泳学习

在研究中，选择典型的鳇科鱼类鲤鱼作为观察对象，将一条19 cm的鲤鱼放在一个70 cm×30 cm×40 cm的鱼缸里，并对其游动状态进行摄像。通过对记录的视频进行分析，提取了3种基本的鲤鱼游泳模式，它们分别是“巡游”、“游动转弯”和“C形急转”。这3种运动模式是鲤鱼最常见的基本运动模式。

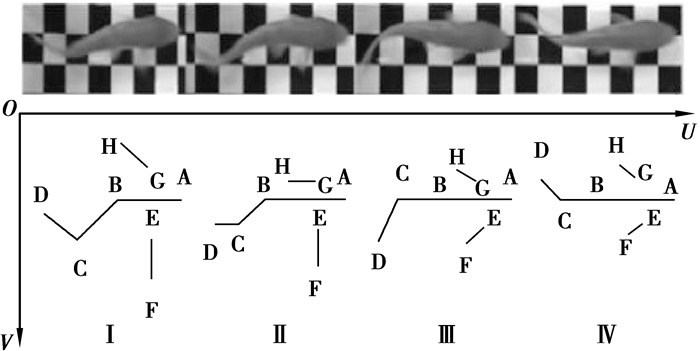
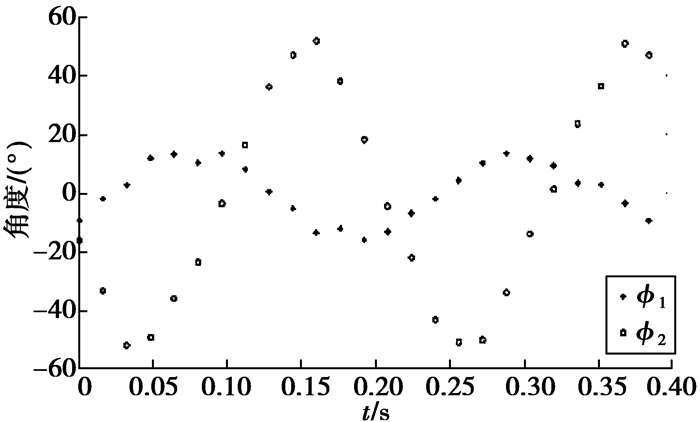
如图 3所示，在“巡游”中，鱼在近似直线的方向上以恒定的速度移动。在所捕获的图像中，鱼通过身体和尾部周期性的拍打获得推进的动力，并利用胸鳍的延展来帮助身体平衡。通过分析，获得了多组在“巡游”模式下的运动轨迹，图 4中的关节角度ϕ₁和ϕ₂即为在“巡游”模式下鲤鱼的运动轨迹。其中，ϕ₁的周期为0.25 s，振幅约为20°；ϕ₂的周期为0.25 s，振幅为60°。

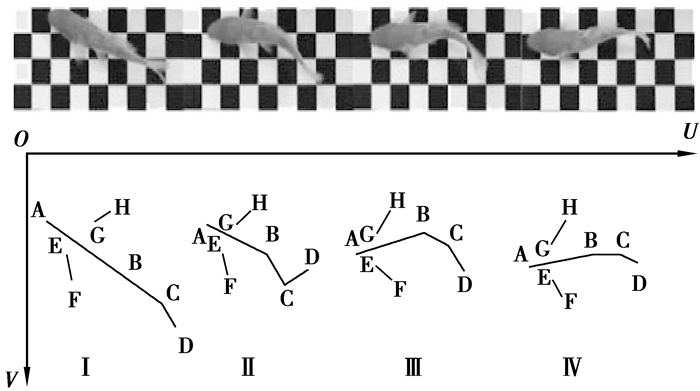
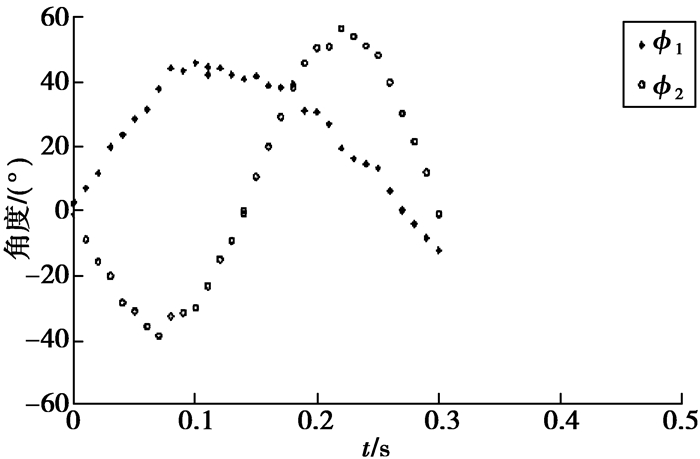
如图 5所示，在“游动转弯”模式下，鱼以很低的角速度和恒定线速度转弯。胸鳍有时协助身体转动，但大多数时候协助身体平衡。图 6显示了关节角度ϕ₁和ϕ₂在“游动转弯”模式下的角度变化情况。其中，ϕ₁的持续时间约为0.3 s，最大幅度约为45°；ϕ₂的持续时间约为0.3 s，最大幅度约为60°。

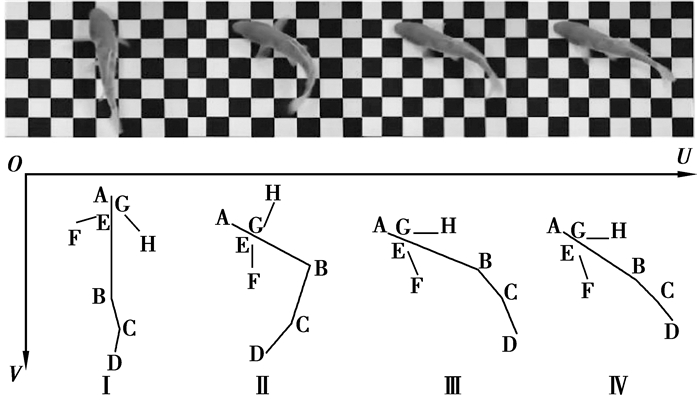
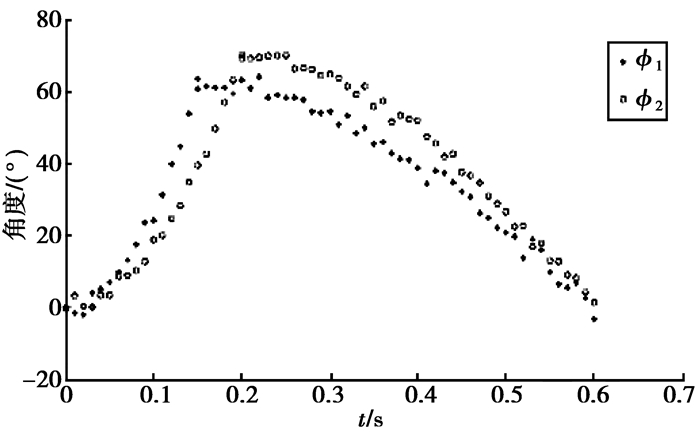
“C形急转”是一类特殊的鱼类运动模式。如图 7所示，在一个非常狭小的空间内鱼为了能很快转弯，通过其身体的尾部变成C形来改变其游动方向，同时扩展它的胸鳍来保持身体平衡。到目前为止，这种运动模式不具有明确的身体运动功能。图 8显示了关节角度ϕ₁和ϕ₂在“C形急转”模式下的角度变化情况。其中，ϕ₁的持续时间约为0.6 s，最大幅度约为65°；ϕ₂的持续时间约为0.6 s，最大幅度约为70°。

3 基于GIM的运动模式学习

鳇科鱼类的运动可以提取为3种基本模式，分别是“巡游”、“游动转弯”和“C形急转”。这些运动主要是通过尾部和鱼鳍的摆动而产生。为了建模并将这些运动模式应用到机器鱼上，采用了一种基于GIM的仿生学习方法。首先通过GIM内嵌的人工神经网络学习真鱼的运动模式，然后利用GIM在时间和空间上的可伸缩性，通过调整相关的GIM参数(如将τ改为ατ)即可得到类似的运动模式，最后将得到的运动模式应用到机器鱼上。

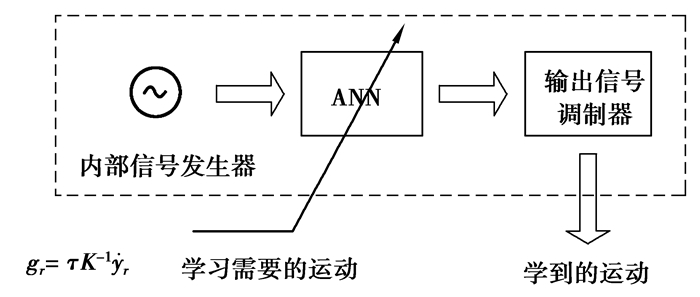
3.1 GIM结构

如图 9所示，GIM的结构由3部分组成，分别是内部信号发生器，人工神经网络和外部信号调制器。内部信号发生器产生持续周期信号作为人工神经网络的输入。人工神经网络从内部信号发生器获得振荡信号后，可以基于非线性映射产生所需的运动模式。外部信号调制器对运动模式进行幅度调制。其数学形式可描述如下：

内部信号发生器

$\begin{array}{l} \tau \dot x = \mathit{\boldsymbol{Ax}},\;\;\;\;\;\;{\mathit{\boldsymbol{x}}_0}\;\;\;\;\;\;{\rm{given}}\\ \mathit{\boldsymbol{A = }}\left[ {\begin{array}{*{20}{c}} 0\\ { - 2{\rm{ \mathsf{ π} }}}\\ {\rm{0}} \end{array}} \right],\\ \mathit{\boldsymbol{x = }}{\left[ {{x_1},{x_2}} \right]^{\rm{T}}}, \end{array}$

(1)

式中：x是内部信号发生器的状态，τ是一个常量因子，其值为生成的节律运动的周期，x₀=[x₁(0), x₂(0)]^T为初始值。

人工神经网络

$g = f\left( \mathit{\boldsymbol{x}} \right),$

(2)

式中:f()是一个非线性映射，x为神经网络的输入，g为神经网络的输出。

外部信号调制器：

$\begin{array}{l} \tau \dot y = \mathit{\boldsymbol{K}}g\;\;\;{\mathit{\boldsymbol{y}}_0}\;\;\;\;{\rm{given}}\\ \mathit{\boldsymbol{K = }}{\rm{diag}}\left( {{k_1}, \cdots ,{k_n}} \right), \end{array}$

(3)

式中：y是外部信号调制器的输出，k_i(i=1，…，n)的输出是一组常数参数，并且y₀=[y₁(0), …, y_n(0)]^T是初始值。K是空间缩放矩阵，τ是常量因子。

GIM不仅可以学习周期节律运动，还可以学习离散运动。离散运动可以看作是节律运动的一个周期的一部分。因此，内部振荡发生器将离散运动作为周期节律运动的一部分。特别地，如果离散运动的持续时间t'给定，则设置节律运动周期τ>t'，这样就可以实现GIM学习了。

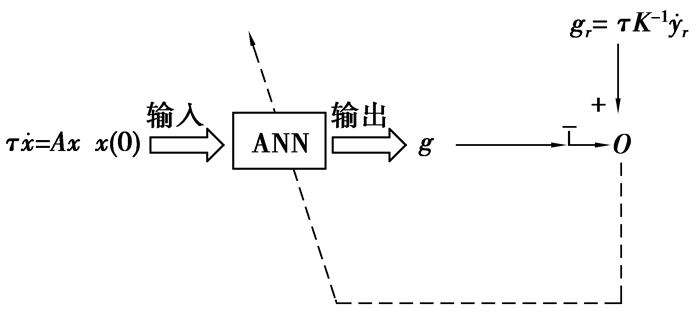
3.2 人工神经网络学习算法

在GIM中，人工神经网络的结构包括3层：输入层、隐含层和输出层。如图 10所示，一旦所需要的量y_r已知，ANN的学习信号就能由公式g_r=τK_r^-1获得。内部信号x作为ANN的输入，而g_r作为预期的输出值，τ为时间常数。之后再通过学习算法进行训练后，ANN就能产生预期的运动模式。

GIM的学习能力完全依赖于ANN的结构和学习算法的能力。在鱼游动模式的学习过程中，由于BP神经网络具有很好的逼近非线性映射特性和泛化能力，选择带惯性项的BP神经网络(Multilayer perceptron: MLP)来精确学习鱼类的运动模式。BP网络的权值学习算法采用最小梯度下降法，激活函数选用Sigmoid函数，由于输入数据维数为2，输出数据维数为1，所以确定网络的输入节点个数为2，输出节点个数为1，隐含层需要的神经元的数量由学习问题的复杂性决定，具体数目需要通过实验或经验给出。通过实验分析比较，最终确定“巡游”、“游动转弯”以及“C形急转”模式学习所采用的隐含层神经元个数分别为10、25和36。

3.3 仿生运动模式的产生

由于机器鱼的尺寸、形状、驱动设备和真正的鱼并不一样，因此真鱼的运动模式很难直接应用到机器鱼上。现已证实GIM对于给定输入输出的时间和空间数量级规模呈线性相关^[15]，这意味着仅通过调整一些GIM参数就能够产生在时间和空间上不同的信号。GIM在时间和空间域的可伸缩性和相移特性如下^[15]：

性质1：时间比例因子α能在时间轴伸展或压缩运动模式。将时间常量τ改为ατ，则外部信号调制器输出(参见公式(3))由y(t)变为y₁(t)。y(t)和y₁(t)关系如式(4)所示。

${\mathit{\boldsymbol{y}}_1}\left( t \right) = y\left( {\frac{t}{a}} \right)。$

(4)

当α>1时，运动周期变长。当α < 1时周期缩短。其实质是改变运动的频率而保持幅度不变。

性质2：空间比例因子β能在空间轴伸展或压缩运动模式，将空间常量k改为βk，并将初始值y(0)改为βy(0)，则系统新的输出y₁(t)和原输出y(t)关系如式(5)所示。

${\mathit{\boldsymbol{y}}_1}\left( t \right) = \beta \mathit{\boldsymbol{y}}\left( t \right),$

(5)

当β>1时，振幅增大。当β < 1时振幅减小。其实质是改变运动的振幅而保持频率不变。

性质3：α和β能在时间轴和空间轴上共同延伸或压缩运动模式。将参数τ改为ατ，k改为βk，初始值y(0)改为βy(0)，则系统新的输出y₁(t)和原输出y(t)关系如式(6)所示。

${\mathit{\boldsymbol{y}}_1}\left( t \right) = \beta \mathit{\boldsymbol{y}}\left( {\frac{t}{\alpha }} \right)。$

(6)

性质4：令初始值y(0)改为y(Δ)，x(0)改为xx(Δ)，则系统新的输出y₁(t)和原输出y(t)关系如式(7)所示。

${\mathit{\boldsymbol{y}}_1}\left( t \right) = \mathit{\boldsymbol{y}}\left( {t + \Delta } \right)。$

(7)

新生成的运动模式的相位超前原运动模式2πΔ/τ。因此，只需要简单修改一下初值即可生成不同相位差的运动模式。

综上，可以通过调节GIM参数α和β对仿生学习得到的真鱼运动模式进行时间或空间上的伸展或压缩，或者通过改变运动的初值，得到适合于机器鱼上的类似的运动模式。

4 实验结果及分析

为证明仿生学习方法的可行性和有效性，将学习得到的3种基本运动模式应用到机器鱼上加以实验验证。并结合红外传感器设计了一个机器鱼避障实验来考察各个基本运动模式的协调工作情况，从而实现了机器鱼的避障功能。

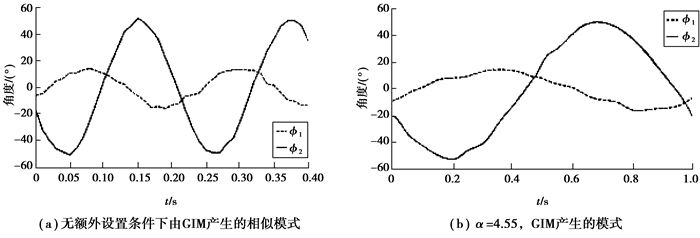
4.1 “巡游”运动模式的产生

根据录像记录的数据显示，鱼类“巡游”模式的驱动是周期性的。此外，根据文献[16]的结论，鱼体在巡游运动中的动作能用波形来描述。因此，“巡游”中关节的运动有相同的周期而不同的相位。首先用一个含有2个输出的GIM产生并协调的相移性质，通过改变GIM的初始值x(0)和y(0)来得到不同的初始相位。一个含有10个隐含神经元的BP神经网络被用来实现非线性映射。由GIM学习得到的ϕ₁和ϕ₂如图 11(a)所示，与图 4所示真鱼的“巡游”运动轨迹具有相似的运动频率和振幅。

然而，由于机器鱼无法移动得像真鱼一样迅速，因此得到的GIM输出不能够直接应用于机器鱼。为了解决这个问题，通过调整参数α将关节运动模式在时间轴上进行延伸。如在图 11(b)所示，在不需要额外训练的情况下，相似的运动能由GIM构造产生。在这个试验中，将α设置为4.55以使关节运动的周期为1 s。图 12展示了机器鱼在“巡游”模式下游动的图像，通过使用在图 11(b)中所示GIM输出的数据。

4.2 “游动转弯”模式的产生

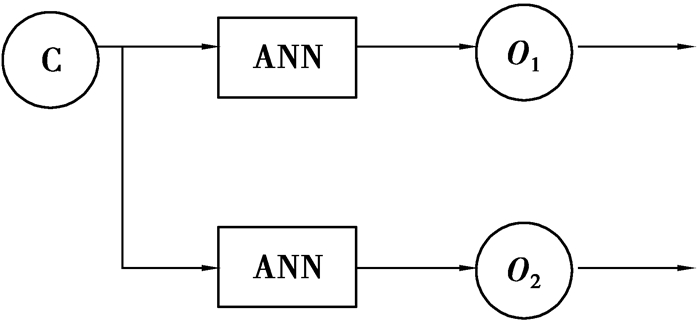
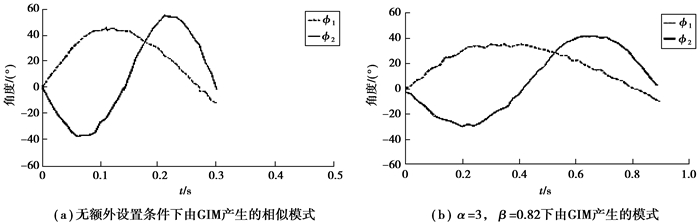
根据所记录的数据显示，在“游动转弯”模式中，关节的运动可以认为是离散运动。这样，设τ=0.3, 这个值大于真鱼在“游动转弯”过程中的持续时间。“游动转弯”模式对应的GIM结构如图 13所示。它包含一个内部信号发生器、2个BP神经网络以及2个外部信号调制器。其中，2个BP神经网络的结构完全相同，其隐含层的节点个数均为25，2个神经网络的输出为ϕ₁和ϕ₂的角度变化轨迹。图 14(a)为由GIM学习得到的ϕ₁和ϕ₂角度变化曲线图，与图 6所示真鱼的“游动转弯”运动模式具有相似的运动轨迹和持续时间。

图 14(b)显示出通过调整参数使α=3，β=0.82，即通过延伸时间和压缩空间使GIM产生类似的可以应用到机器鱼上的运动模式。在此实验中，“游动转弯”仅在1 s内完成。图 15展示了通过使用在图 14(b)中所示GIM输出的数据，完成了机器鱼“游动转弯”模式下游动。

4.3 “C形急转”游泳模式的产生

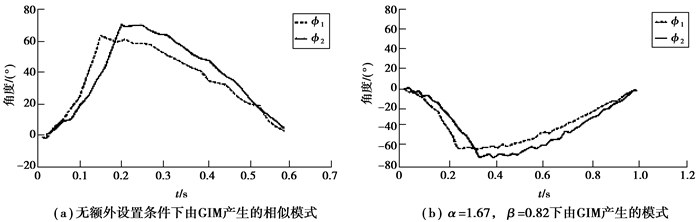
在“C形急转”中，关节的运动也是离散运动。根据对所记录的数据分析得知，运动过程的持续时间低于0.8 s，这样，设τ=0.8。“C形急转”模式的GIM结构和“游动转弯”是一样的。2个BP神经网络均包含36个隐含神经元。图 16(a)即为通过GIM得到的ϕ₁和ϕ₂角度变化曲线图。与图 8所示真鱼的“C形急转”运动模式具有相似的运动轨迹和持续时间。

此实验中，试图让机器鱼学习向右急转，而图 16(a)是学习真鱼的向左急转。为得到期望的运动，设置α=1.67，β=-1从而得到相移180°、持续时间为1 s的适合于机器鱼的运动模式。图 17展示了机器鱼在“C形急转”模式下游动的图像。

4.4 基于红外传感器的机器鱼避障实验

为了考察各个基本运动模式的协调工作情况，提出了集成多个红外传感器实现机器鱼避障的控制方案，通过一种基于规则推理的智能避障控制算法，实现了机器鱼基本的避障功能。

采用了3个红外传感器，分别安装在机器鱼头部的前、左和右侧。首先，通过红外传感器采集周围障碍物的距离信息，并将采集到的距离数据进行模糊化，比如说将前方障碍物的距离值分成3档：近、较远、很远，分别对应距离值0~15 cm、15~35 cm和>35 cm，距离值经模糊化处理后作为系统输入。然后再根据已导入的规则库和推理策略对输入进行推理，得到输出。相应的推理规则表如表 1所示。

其中:N、F表示障碍物的距离较近和较远；TR、TL和FW表示机器鱼右转、左转和前进。最后，将输出转换为相应的动作激励驱动舵机转动相应的角度，从而实现机器鱼的避障。

实验结果如图 18所示。首先，机器鱼“巡游”向前(图 18(a))，游到水槽右上角处时，由于前方和右方都存在障碍物(水槽壁)，机器鱼“游动左转”(图 18(b))，继续“巡游”到图 18(c)所示位置时，由于障碍物(槽壁)距离太近，机器鱼“C形急转”避开障碍物，此后继续“巡游”向前。靠近圆形障碍物时，机器鱼“游动左转”(图 18(d))。通过实验，发现机器鱼可以灵活地调用各种基本运动模式轻松地避开障碍物，实现自主漫游。

5 结论

研究中采用了基于GIM模型的仿生学习方法构建仿生机器鱼。首先，通过对鳇科类鲤鱼的运动行为进行观察、数据采集和分析，提取出了3种基本的运动模式。其次，采用GIM模型对这3种运动模式进行学习。GIM方法在时间和空间上的可伸缩性对研究鱼的运动模式提供了很大的灵活性，可以通过调整GIM参数产生各种运动模式，从而避开了繁杂的学习或训练过程。最后，构建的仿生机器鱼实现了鲤鱼的3种基本运动模式，并结合红外传感器和模糊控制实现了机器鱼避障功能。实验结果验证了该方法的有效性和可行性。