2. 国网重庆市电力公司 江北供电分公司, 重庆 401147
2. Chongqing Jiangbei Branch of State Grid Corporation of China, Chongqing 401147, P.R.China
聚类分析是数据挖掘领域的研究热点,是人们认识和探索事物之间内在联系的有效手段。聚类分析就是把对象按照性质上的亲疏程度分成多个类或簇,使得类或簇内的数据具有较高相似度,类或簇间的数据具有较高的相异度[1]。它不需要先验知识或假设,因此是一种无监督的学习过程。传统的聚类算法有k-means算法、EM算法、模糊C均值(FCM)等。这些算法仅在具有凸形结构的样本空间上有较好的效果,而当样本空间为非凸时,算法易陷入局部最优解。
谱聚类算法是近年来广受关注的一种高性能计算方法,它建立在谱图划分理论基础上,将聚类问题转化为图的最优划分问题,使得子图内部的相似度最大,子图之间的相似度最小[2]。谱聚类算法克服了传统聚类算法的缺点,具有明显的优势。比较典型的谱聚类算法有Perona和Freeman提出的PF算法[3],Shi和Malik提出的SM算法[4],Ng、Jordan和Weiss等[5]提出的NJW算法。其中NJW算法要首先根据样本空间构建相似度矩阵W,这会涉及尺度参数σ的选取问题,σ的取值对聚类结果影响较大,往往依赖于领域知识和个人经验。Ng等[5]同时也给出了一种选择σ的方法,通过反复运行NJW算法来自动确定σ的大小,这消除了人为因素,却增加了运算时间。文献[6]提出了一种自调整的谱聚类算法,该算法为每个样本点指定一个σi,以此取代全局σ构建相似度矩阵,然而,σi的确定也依赖于一定的经验值。此外,当处理大规模数据集时,构造相似度矩阵和求取拉普拉斯矩阵的特征向量都需要很大的内存开销和计算时间。对此问题,Fowlkes等[7]提出使用Nyström逼近方法减少求解特征问题的计算复杂度;Yan等[8]提出利用K均值算法或者RP-tree将数据分成若干微簇,然后对每个微簇选择的代表点进行聚类,最后对应得到所有数据的类标。
以NJW谱聚类算法为基础,提出了一种基于K近邻的自适应谱聚类快速算法(Fast algorithm for adaptive spectral clustering based on K-nearest neighbors,FA-SC)。该算法能够根据输入数据集的空间分布,自动地确定自适应尺度参数σi,用于取代全局值,消除了人为选取参数的不确定性,使聚类结果更符合实际;同时,对输入数据集分块计算,构造基于K近邻的相似度矩阵W,并对W进行稀疏化处理,大大减少了内存开销和计算复杂度。实验结果表明,提出的FA-SC算法简化了输入参数的选取,减少了运行时间,能够更有效地处理大数据集聚类问题。
1 谱聚类算法谱聚类的思想来源于谱图划分理论[9]。假定将每个数据样本看作图G中的顶点V,根据样本间的相似度将顶点间的边E赋权重值,就得到一个基于样本相似度的无向加权图G (V,E),那么聚类问题就转化为图G的最优划分问题,划分准则就是使划分成的子图内部相似度最大,子图之间的相似度最小。考虑问题的连续放松形式,可将图划分问题转换成求解相似矩阵或拉普拉斯矩阵的谱分解,可以认为谱聚类是对图划分准则的逼近[10]。
1.1 图的矩阵表示谱聚类首先构造样本空间的相似度矩阵,用W(W∈Rn×n)表示。相似矩阵中包含了聚类所需的全部信息,如果相似矩阵具有优良的性质,可以预期谱聚类算法的表现也会令人满意。通常用高斯核函数计算W,由公式(1)给出。其中,xi,xj表示不同的样本点,
| wij={exp(−xi−xj22σ2),i≠j;0,i=j。 | (1) |
将相似度矩阵W的每行元素相加,得该顶点vi(vi(V)的度di,由公式(2)定义,以所有度值为对角元素构成的对角矩阵称为度矩阵,通常用D表示。
| di=n∑j=1wij, | (2) |
图的拉普拉斯矩阵分为非规范型和规范型2种。非规范型拉普拉斯矩阵表示为:L=D-W。规范型拉普拉斯矩阵有2种形式,用公式(3)和公式(4)表示。选用不同的拉普拉斯矩阵所得的聚类结果也会有差别。如何根据具体环境选择合适的拉普拉斯矩阵,还需进行大量的理论研究和实验工作。
| Lsys=D−12WD−12, | (3) |
| Lrw=D−1W。 | (4) |
研究提出的基于K近邻的自适应谱聚类快速算法(FA-SC)是以NJW算法为基础,因此,给出NJW算法的处理过程[5]为
1)根据公式(1)构造样本空间的相似度矩阵W(W∈Rn×n),取欧氏距离,尺度参数σ由人为指定。
2)根据公式(3)计算规范化的拉普拉斯矩阵Lsys,求解Lsys的前k个最大特征值对应的特征向量x1,x2,…xk(必要时正交化处理),建立矩阵X=[x1, x2, …xk],其中xi为列向量。
3)对X的行向量归一化处理,处理后得到矩阵Y,其中
4)将矩阵Y的每一行看成是Rk空间中的一个数据点,使用k-means算法把n行数据分为k个聚类A1,A2…Ak。
5)当矩阵Y的第i行在类Aj中时,划分原样本空间中样本点xi到Cj类。
从NJW算法的实现过程可知,使用高斯核函数构造相似度矩阵W,其中,尺度参数σ要求人工设置,而σ的取值依赖于领域知识和经验,没有一定的规律可循,其取值将直接影响聚类结果的好坏。并且,相似度矩阵W中保存了所有样本点之间的信息,然而在实际中,并不是每2个点的wij都是有意义的。尤其对于大规模数据集来说,计算、存储相似度矩阵和特征向量都需要较大的时间和内存开销,非常不利于算法的扩展。
2 基于K近邻的自适应谱聚类快速算法(FA-SC)如何自动的确定尺度参数σ,加快算法运行速度,并作用于大规模数据集,是研究工作的关键。因此,提出了一种基于K近邻的自适应谱聚类快速算法(FA-SC算法),该算法的处理过程与NJW算法相似,区别在于第一步中构造相似度矩阵和加快算法运行速度。具体的研究工作分为以下几个部分:
1)根据样本分布自动确定合适的尺度参数σ;
2)对输入数据集分块处理,将构造相似度矩阵W的过程分成多步进行;
3)采取保存样本点K个最近邻的距离值wij的策略,对相似度矩阵W进行稀疏化处理。
2.1 尺度参数σ的选取通过手动设置尺度参数σ的值是很困难的,σ的取值应适应样本的具体分布,全局值的σ难以反映出这种分布情况[11]。考虑到采用全局σ的局限性,不妨对每个样本点定义一个自适应尺度σi,使样本点具备“自适应尺度”的属性[12]。σi的取值由样本点xi的K个最近邻决定,其计算方法由公式(5)给出。
| σi=1KK∑m=1xi−xm。 | (5) |
由公式(5)可知,σi表示样本点xi和其K个最近邻距离的平均值,因此,σi称为近邻自适应尺度,相应的相似度矩阵W可由公式(6)定义。
| wij={exp(−xi−xj2σi⋅σj),i≠j;0,i=j。 | (6) |
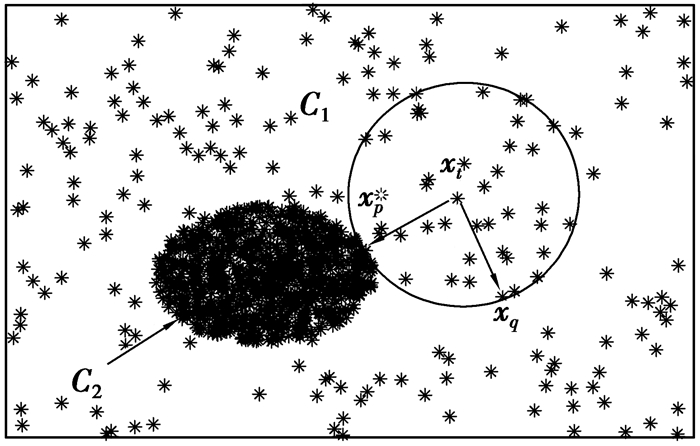
σi反映了近邻分布的变化,能够自适应于局部结构,使簇内点的相似度增大,簇间点的相似度减小。以图 1为例,图中分布着2个密度相差较大的簇C1和C2,且xt、xq∈C1,xp∈C2,xp和xq均在xt的K邻域内。为便于说明问题,这里假设xt-xp=xt-xq,由于簇C1密度小于簇C2,由公式(5)可得近邻自适应尺度σp < σq,再由公式(6)可得wtp < wtq,若采用全局尺度参数,由公式(1)可得wtp=wtq。显然,采用近邻自适应尺度可使同一簇中样本间wij值大于不同簇中的相应值,这样更利于聚类。
|
图 1 近邻自适应尺度原理 Figure 1 Principle of nearest-neighbor scaling |
谱聚类的运行过程中不可避免的要计算拉普拉斯矩阵的特征值与特征向量,非稀疏矩阵的计算复杂度为O(n3)。同时考虑对海量数据聚类的情况,假设输入数据集的规模为n,则要根据公式(7)计算Cn2次欧氏距离。此时计算的相似度矩阵W中共保存了n2个数据值,计算这些数据也要考虑时间和内存的开销。
| ‖xi−xj‖2=‖xi‖2+‖xj‖2−xTixj。 | (7) |
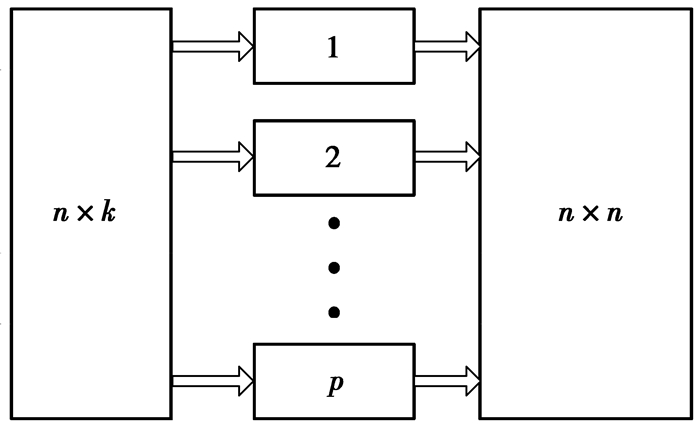
为了减小一次计算的内存消耗,在计算样本欧氏距离的过程中,采取多步计算的方法,将输入数据集分成若干块,分别计算每一块与整个样本的距离值,最后将每步计算的结果合并,得到距离矩阵。由于每一块的数据规模远小于n,这样就大大降低了内存负担。数据集分块计算的过程由图 2所示。
|
图 2 数据集分块计算过程 Figure 2 The calculating procedure of data set blocks |
数据集分块计算虽然减轻了一次计算的内存开销,但要保存距离矩阵依然要占用较大的系统资源,甚至会超出计算机的内存。一个好的方法是对距离矩阵进行稀疏化处理,考虑到对每个样本点都要计算n次距离,这n个距离值中大部分属于无意义的信息,其中离样本点越近的距离值对聚类结果的影响往往越大。因此,为了得到稀疏距离矩阵,只保存样本点的K个最近邻的距离值,其他值归零,这样便可获得稀疏化的距离矩阵,再由稀疏距离矩阵利用公式(6)、(3)可进一步构造稀疏化的相似度矩阵W和拉普拉斯矩阵Lsys,根据稀疏化的拉普拉斯矩阵Lsys计算特征值和特征向量将变得简单[13]。
3 实验与分析为验证提出的FA-SC算法的有效性,作者将该算法与NJW算法作对比,在人工数据集和UCI数据集上做了3组实验。实验环境为Intel Core 2 E7400处理器,2GB内存,Windows XP SP3操作系统,matlab平台。
3.1 尺度参数自适应实验NJW算法在运行之前需要手动设置全局尺度参数σ,且σ的取值会对聚类结果产生影响,这使它在应用上具有极大的局限性。FA-SC算法能够很好的克服NJW算法的不足,根据输入样本的分布自动地选取尺度参数以获取最佳的聚类效果。作者在3个人工数据集D1、D2、D3上进行了验证,对比实验的结果如图 3~图 5所示。
|
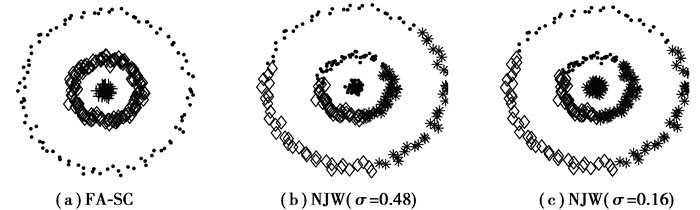
图 3 数据集D1上聚类结果 Figure 3 Clustering results of data set D1 |

|
图 4 数据集D2上聚类结果 Figure 4 Clustering results of data set D2 |
|
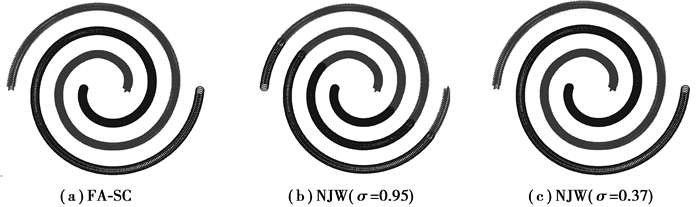
图 5 数据集D3上聚类结果 Figure 5 Clustering results of data set D3 |
作者在3个数据集上选取了多组参数进行实验。图 3、4中的数据集都有3个簇,分别改变NJW算法中尺度参数σ的值,均得到了错误的聚类结果,只有FA-SC算法发现了正确的簇。图 5中的数据集有2个簇,当尺度参数σ=0.37时,NJW算法得到了正确的聚类结果,改变σ的取值会导致错误的划分。对比试验说明,NJW算法的聚类结果易受尺度参数σ的影响,而σ的取值很难确定,提出的FA-SC算法能够自适应地选取σ值,不用手动设置,实现了较好的聚类效果。
3.2 算法复杂度分析假设输入的样本空间为n×d(n表示样本容量,d表示维度)。FA-SC算法第一步计算样本点间欧氏距离并获得基于K近邻的稀疏距离矩阵,其时间复杂度为O(n2d)+O(n2logK),空间复杂度为O(nK);第二步计算各样本点的近邻自适应尺度参数σi,时间复杂度为O(nK);第三步求解规范化拉普拉斯矩阵Lsys的k个最大特征值和特征向量,采用文献[12]使用的ARPACK计算方法[14],其时间复杂度为(O(m3)+(O(mn)+O(nK))×O(m-k))×I,空间复杂度为O(nK)+O(mn),其中,m通常取值约为k几十倍,I为迭代次数,最后调用一次k-means算法,时间复杂度为O(Ik2n),其中,I为迭代次数,且I < < n。
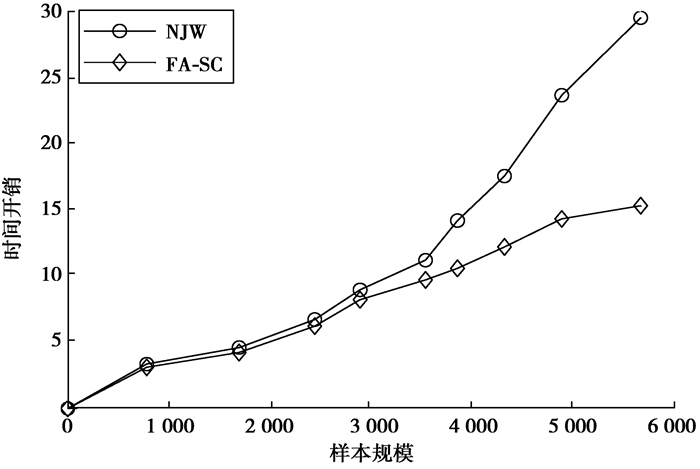
图 6中将FA-SC算法与NJW算法对比,测试2种算法在不同规模样本集上的时间开销。从图 6中可以看到,FA-SC算法执行速度比NJW算法快,而且随着样本规模的增加,这种执行速度的差距也越来越明显。这表明,FA-SC算法降低了聚类时间开销,对数据集的规模大小具有很好的扩展性。
|
图 6 两种算法聚类时间对比 Figure 6 Contrastive time complexity of the two algorithms |
为了更客观的评价聚类结果,笔者在几个UCI真实数据集上作对比试验,评价聚类结果的准确率。采用文献[15]使用的Rand指标计算准确率,假设C为参考聚类结果,P为实际聚类结果,则准确率的计算方法由公式(8)给出(其中,a:属于C、P中同一类的样本对数目;b:属于C中同一类,P中不同类的样本对数目;c:属于C中不同类,P中同一类的样本对数目;d:属于C中不同类,P中不同类的样本对数目)。
| RI=a+da+b+c+d。 | (8) |
表 1为FA-SC算法与NJW算法的准确率对比,由对比结果可知,FA-SC算法比NJW算法的准确性较高。
| 表 1 聚类结果准确率对比 Table 1 Contrastive accuracy rate of the clustering results |
分析了传统NJW谱聚类算法的原理和不足,提出了一种基于K近邻的自适应快速谱聚类算法(FA-SC),能够根据输入数据集的分布自动确定尺度参数,简化了NJW算法的参数选取;同时,针对大数据集的情况,采用数据集分块计算策略构造稀疏化的相似度矩阵,减小了计算特征值和特征向量的内存开销和时间复杂度。在多个数据集上的实验结果表明,该算法可以产生较好的聚类结果并提高了聚类速度。然而,FA-SC算法依然需要事先给出样本的聚类数目,事实上,这也是谱聚类算法的难题之一。下一步,还要在如何自动确定给定数据集的最佳聚类数目上做进一步研究。
| [1] | Jain A K, Murty M N, Flynn P J. Data clustering: a review[J]. ACM Computing Surveys, 1999, 31(3): 264–323. DOI:10.1145/331499.331504 |
| [2] | Filippone M, Camastra F, Masulli F, et al. A survey of kernel and spectral methods for clustering[J]. Pattern Recognition, 2008, 41(1): 176–190. DOI:10.1016/j.patcog.2007.05.018 |
| [3] | Perona P, Freeman W T. A factorization approach to grouping[C]//5th European Conference on Computer Vision Freiburg, June, 2-6, 1998, Germany. Springer-Verlag: Springer Berlin Heidelberg, 1998, 1406: 655-670. |
| [4] | Shi J, Malik J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888–905. DOI:10.1109/34.868688 |
| [5] | Ng A Y, Jordan M I, Weiss Y. On spectral clustering: analysis and an algorithm[J]. Advances in Neural Information Processing Systems, 2001, 14: 849–856. |
| [6] | Zelnik-Manor L, Perona P. Self-tuning spectral clustering[J]. Advances in Neural Information Processing Systems, 2004: 1601–1608. |
| [7] | Fowlkes C, Belongie S, Chung F, et al. Spectral grouping using the Nystrom method[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(2): 214–225. DOI:10.1109/TPAMI.2004.1262185 |
| [8] | Yan D, Huang L, Jordan M I. Fast approximate spectral clustering[C]//Proceedings of the 15th ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, New York, USA: IEEE, 2009:907-916. |
| [9] | Fiedler M. Algebraic connectivity of graphs[J]. Czechoslovak Mathematical Journal, 1973, 23(2): 298–305. |
| [10] | Malik J, Belongie S, Leung T, et al. Contour and texture analysis for image segmentation[C]//Perceptual Organization for Artificial Vision Systems. US: Springer, 2000, 546: 139-172. |
| [11] |
卜德云, 张道强.
自适应谱聚类算法研究[J]. 山东大学学报:工学版, 2009, 39(5): 22–26.
BU Deyun, ZHANG Daoqiang. Adaptive spectral clustering algorithm research[J]. Journal of Shandong University: Engineering Science, 2009, 39(5): 22–26. (in Chinese) |
| [12] |
谷瑞军, 叶宾, 须文波.
一种改进的谱聚类算法[J]. 计算机研究与发展, 2007, 44(z2): 145–149.
GU Ruijun, YE Bin, XU Wenbo. An improved spectral clustering algorithm[J]. Journal of the Computer Research and Development, 2007, 44(z2): 145–149. (in Chinese) |
| [13] | Chen W Y, Song Y Q, Bai H J, et al. Parallel spectral clustering in distributed systems[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(3): 568–586. DOI:10.1109/TPAMI.2010.88 |
| [14] | Lehoucg R B, Sorensen D C, Yang C. ARPACK users' guide : solution of large-scale eigenvalue problems with implicitly restarted Arnoldi methods[M]. [s. n.]: SIAM, 1998. |
| [15] | Halkidi M, Batistakis Y, Vazirgiannis M. On clustering validation techniques[J]. Journal of Intelligent Information Systems, 2001, 17(2-3): 107–145. |
 2015, Vol. 38
2015, Vol. 38


