交通拥堵问题日趋严峻，严重影响了人类的生活和制约了社会经济的发展。为了解释交通拥堵形成机理及其演化规律，国内外学者提出了诸如跟驰模型，元胞自动机模型和宏观动力学模型等交通流模型^[1-3]。例如，Bando等^[4]提出的优化速度(Optimal velocity, OV)模型是一种被广泛研究的跟驰模型，该模型可以描述诸如时走时停、阻塞相变等实际交通现象。1998年，Helbing和Tilch^[5]为克服OV模型中过高的加速度和不实际的减速度现象，通过考虑连续前后2车之间的速度差影响，提出广义力模型(Generalized force GF)。2001年，JIANG等^[6]指出前后车间的正速度差对跟驰行为也有影响，在GF模型基础上提出了全速度差模型(Full velocity difference FVD)。研究表明，FVD模型的动态性能优于OV和GF模型。近年来，信息化条件下的交通流建模研究日益活跃。一系列基于FVD的扩展模型相继提出^[7-9]。彭光含等^[10-11]基于FVD模型，考虑前后车的优化速度差信息，建立一种优化速度差的跟驰(Optimal velocity difference, OVD)模型，仿真结果表明该模型较FVD模型，交通流稳定性能得到明显增强。

上述研究表明，利用最紧邻前车的位置信息、前后车相对速度信息和优化速度信息均可增强交通流的稳定性，有效地抑制交通阻塞现象。然而，事实上，跟驰车驾驶员通过车车通信技术可以获得前车的运动状态变化趋势即加速度，这样可以及时合理地调整自身的状态，从而保证车辆安全稳定有序地运行^[12]。但以上研究中模型均未涉及最紧邻前车加速度信息对交通流稳定性的影响。因此，研究在OVD模型的基础上，考虑最紧邻前车加速度信息对跟驰行为的影响，提出一个含加速度项(Optimal velocity difference & acceleration OVDA)的跟驰模型。利用线性稳定性理论得到车流运行稳定的条件，同时，在周期边界条件下对该模型进行数值仿真，以验证模型的性能和合理性。

1 模型

1995年，Bando等^[4]在经典跟驰模型基础上提出优化速度模型，其运动学方程为^[4]

$\frac{{{\rm{d}}{v_n}\left( t \right)}}{{{\rm{d}}t}} = \alpha \left[ {V\left( {\Delta {x_n}\left( t \right)} \right) - {v_n}\left( t \right)} \right],$

(1)

式中：α为敏感系数; V(·)称为是车头间距Δx_n(t)=x_n+1(t)-x_n(t)的优化速度函数；x_n+1(t)和x_n(t)分别为t时刻第n+1、n辆车的位置，v_n(t)为车辆n在t时刻的速度。该模型能够较好地描述一些诸如交通阻塞的传播、时走时停等实际交通现象。

1998年，Helbing^[5]利用相关设备得出的实测数据对OV模型进行了参数辨识，发现该模型有不切实际的减速度和过高加速度等缺点，因此，对OV模型进行改进，提出了GF模型^[5]

$\frac{{{\rm{d}}{v_n}\left( t \right)}}{{{\rm{d}}t}} = \alpha \left[ {V\left( {\Delta {x_n}} \right) - {v_n}\left( t \right)} \right] + \lambda \Delta {v_n}H\left( { - \Delta {v_n}} \right),$

(2)

式中Δv_n=v_n+1-v_n为车辆的相对速度，H(-Δv_n)是Heaviside阶梯函数，λ是对最紧邻前车相对速度的反应系数。尽管该模型避免了OV模型中出现的过高加速度的情况，然而却出现了延迟时间较长的现象，同时也不能解释正速度差效应，即Treiber等^[13]人指出跟驰车辆速度比最紧邻前车小很多时，尽管前后车距离小于安全距离，跟驰车也不会减速的现象。因此2001年，Jiang等^[6]人基于GF模型提出了全速度差(Full velocity difference, FVD)模型，其运动学方程为

$\frac{{{\rm{d}}{v_n}\left( t \right)}}{{{\rm{d}}t}} = \alpha \left[ {{V_F}\left( {\Delta {x_n}} \right) - {v_n}\left( t \right)} \right] + \lambda \Delta {v_n},$

(3)

模型中参数物理意义与GF模型一致。彭光含等人^[10]在FVD模型的基础上，进一步考虑前后车的优化速度差信息对车流的影响，提出了OVD模型

$\begin{array}{l} \frac{{{\rm{d}}{v_n}\left( t \right)}}{{{\rm{d}}t}} = \alpha \left[ {{V_F}\left( {\Delta {x_n}\left( t \right)} \right) - {v_n}\left( t \right)} \right] + \lambda \Delta {v_n}\left( t \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\gamma \left[ {V\left( {\Delta {x_{n + 1}}\left( t \right)} \right) - V\left( {\Delta {x_n}\left( t \right)} \right)} \right], \end{array}$

(4)

式中：V(Δx_n+1)和V(Δx_n)分别是第n+1、n辆车在t时刻的最优速度; V(Δx_n+1)-V(Δx_n)为第n+1、n辆车的最优速度差。仿真表明OVD模型性能较FVD模型更好，即考虑前后车的优化速度差信息能够增强车流的稳定性。

上述模型在一定程度上能描述实际交通现象，同时，利用最紧邻前车的状态信息来提高车流的稳定性能，从而有效地抑制交通拥堵。伴随智能交通系统的快速发展，通过车载智能终端可实现车辆信息的实时交互。因此，任何车辆均可获得前后附近车辆的信息，用来调整自身运行状态达到最优。而OVD模型只考虑了优化速度信息、速度信息和位置信息，并未考虑最紧邻前车加速度信息对交通流的稳定性造成何种影响。鉴于此，考虑最紧邻前车加速度信息对当前车的跟驰行为的影响，在OVD模型的基础上，提出考虑最紧邻前车加速度信息OVDA (Optimal velocity difference & acceleration)跟驰模型, 其运动学方程为

$\begin{array}{l} \frac{{{\rm{d}}{v_n}\left( t \right)}}{{{\rm{d}}t}} = \alpha \left[ {V\left( {\Delta {x_n}\left( t \right)} \right) - {v_n}\left( t \right)} \right] + \lambda \Delta {v_n}\left( t \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\gamma \left[ {V\left( {\Delta {x_{n + 1}}\left( t \right)} \right) - V\left( {\Delta {x_n}\left( t \right)} \right)} \right] + p{a_{n + 1}}\left( t \right), \end{array}$

(5)

式中：a_n+1(t)为第n+1辆车在t时刻的加速度信息；p表示驾驶员对加速度信息的关注系数。当p=0时，模型将不考虑加速度效应的影响，OVDA模型将退化为OVD模型。本模型采用如下的最优速度函数^[6]

$V\left( {\Delta x} \right) = {V_1} + {V_2}\tanh \left[ {{C_1}\left( {\Delta x - {l_c}} \right) - {C_2}} \right]。$

(6)

2 线性稳定性分析

为了研究加速度效应对交通系统稳定性的影响，下面应用线性稳定性理论分析OVDA模型。设初始车辆的车头间距均为b=L/N(N表示车辆数，L表示道路的长度)，优化速度为V(b)。此时，均匀稳态交通流的车辆位置解为

$x_x^{\left( 0 \right)}\left( t \right) = bn + V\left( b \right)t,$

(7)

施加一小扰动y_nt=e^ikn+zt添加到的方程(7)

${y_n}\left( t \right) = {x_n}\left( t \right) - x_n^0\left( t \right),$

(8)

将式(8)代入方程(5)，并线性化得到

$\begin{array}{l} y''{}_n\left( t \right) = a\left[ {V'\left( b \right)\Delta {y_n}\left( t \right) - y'{}_n\left( t \right)} \right] + \lambda \Delta y'{}_n\left( t \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\gamma V'\left( b \right)\left[ {\Delta {y_{n + 1}}\left( t \right) - \Delta {y_n}\left( t \right)} \right] + py''{}_{n + 1}\left( t \right) = 0 \end{array}$

(9)

式中：Δy_n(t)=y_n+1(t)-y_n(t)，V′(b)=d(V(Δx_n(t)))/d(Δx_n(t))|_Δxn(t)=b，将方程(9)中的y_n按傅里叶级数展开，得到

$\begin{array}{l} {z^2}\left( {1 - p{e^{ik}}} \right) + \left[ {a - \left( {{e^{ik}} - 1} \right)\lambda } \right]z - \\ aV'\left( b \right)\left( {{e^{ik}} - 1} \right) - \gamma V'\left( b \right)\left[ {{e^{2ik}} - 2{e^{ik}} + 1} \right] = 0。 \end{array}$

(10)

对方程(10)中参数z按照z=z₁(ik)+z₂(ik)²+…展开，式中

${z_1} = V'\;{}_b,$

(11)

${z_2} = \frac{{a + 2\lambda + 2\gamma }}{{2a}}V'\left( b \right) - \frac{{\left( {1 - p} \right)}}{a}{\left( {V'\left( b \right)} \right)^2},$

(12)

式中：τ=1/a，λ=k/τ，如果z₂ < 0，则初始均匀的车流在小扰动下会变得不稳定，反之，车流在小干扰下会演化为稳定均衡状态。因此，OVDA模型的中性稳定条件如下

$V'\left( b \right) = \frac{{a + 2\lambda + 2\gamma }}{{2\left( {1 - p} \right)}}。$

(13)

车流运行稳定条件如下

$V'\left( b \right) < \frac{{a + 2\lambda + 2\gamma }}{{2\left( {1 - p} \right)}}。$

(14)

当p=0时，可以得与OVD模型一致的稳定性条件

$V'\left( b \right) < \frac{a}{2} + \lambda + \gamma 。$

(15)

通过比较OVDA模型的稳定性判据式(14)与OVD模型的稳定性判据式(15)可以发现：由于考虑了最紧邻前车加速度信息对车流的影响，在区域$\frac{a}{2} + \lambda + \gamma < V'(b) < \frac{{a + 2\lambda + 2\gamma }}{{2\left( {1-p} \right)}}$内进一步稳定了交通流，这意味着OVDA模型对交通流有进一步的致稳性能，因此，充分显示了最紧邻前车加速度信息对车辆的跟驰行为具有不可忽视的影响。

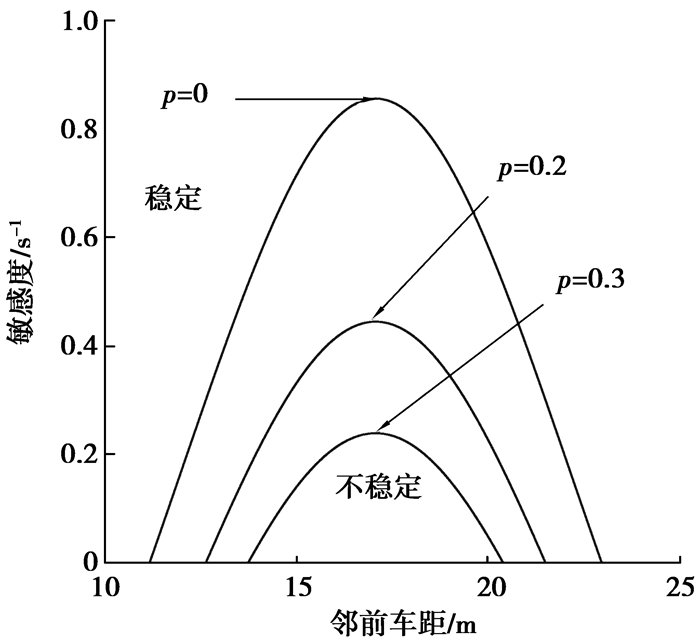
在图 1参数(Δx, a)相空间中，实线为临界稳定曲线，临界稳定曲线以上为稳定区域；临界稳定曲线以下为不稳定区域。从图 1中可以更直观得到与线性稳定性分析一致的结果，OVDA模型的稳定区域较OVD模型的更大，说明车辆在一定的范围内平稳有序的行驶，有效抑制交通拥堵。同时，图 1清晰地给出了随着驾驶员关注最紧邻前车加速度信息的程度不断增加，敏感度不断减低，稳定性区域不断增大，这是OVDA模型考虑了加速度信息的结果，说明在OVDA模型中关注加速度信息，稳定区域将进一步增大说明车辆能在较大范围内平稳的行驶。

3 数值模拟 3.1 启动过程对比仿真

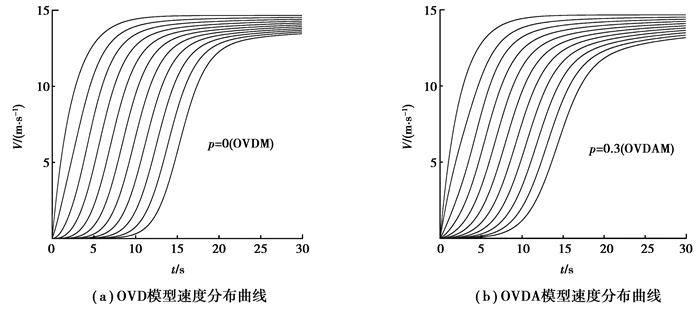
下面研究OVDA模型在黄灯转向绿灯的交通信号灯环境下的车辆启动情况，并检验OVDA模型的动态特性。模拟静止车队的启动过程：在t < 0时，交通信号为红灯，11辆车排成一队，每辆车的初始位置为x_n(0)=(n-1)d，其中n=1, …, 11，d=7.4 m，所有车辆初始状态都处于静止状态，及v_n(0)=0，(n=1, 2, …, 11)；在t=0时，红灯转绿，车辆开始启动。其它边界条件：对于头车n=11，最优速度函数为V₁₁(∞)=14.66 m·s^-1，对于跟随车，有V_n(7.4)=0, (n=1, …, 10)。为了与OVD模型作对比实验，设置2个模型的参数相同。在模拟中，可以得到车辆运动延迟时间δt。由此，还可以计算出车辆启动波速c_j=7.4/δt。选取γ=0.1和a=0.41 s^-1，并选取Helbing和Tilch对实测数据进行参数辨识得到的OV函数式(6)，模拟结果如图 2所示。图 2给出了车辆启动过程中速度的分布曲线，从图 2中可以得到运动延迟时间δt，表 1列出了OVD模型和OVDA模型的运动延迟时间和启动波速。由表 1中可以看到由OVDA模型预测的车辆运动延迟时间和启动波速与实测值非常接近^[11]。

OVDA模型描述的车辆速度曲线最快趋于最大值，这表示OVDA模型在启动阶段的时间相较于OVD模型更短，因为跟随车驾驶员可以直接获得前车运动状态趋势，及时调整车辆状态，缩短车辆运动延迟时间，这符合实际驾驶行为。根据上述分析，OVDA模型在启动过程中，在速度特性方面优于OVD模型。

3.2 演化过程对比仿真

为了更加直观分析紧邻前车加速度信息对车流稳定性的作用，现利用数值模拟以验证OVDA模型演化特性。设周期边界条件为：L=1 500 m，车辆数N=100，对头车施加小扰动x₁(0)=L/N+1下，敏感系数选取a=0.41 s^-1，其他参数λ=0.3, γ=0.05, p=0.3。车辆的初始条件如下

$\begin{array}{l} {x_1}\left( 0 \right) = 1{\rm{m,}}\\ {x_n}\left( 0 \right) = \left( {n - 1} \right)L/N\left( {n = 2,3, \cdots ,N} \right),\\ {v_n}\left( 0 \right) = V\left( {L/N} \right)\left( {N = 1,2, \cdots ,N} \right)。 \end{array}$

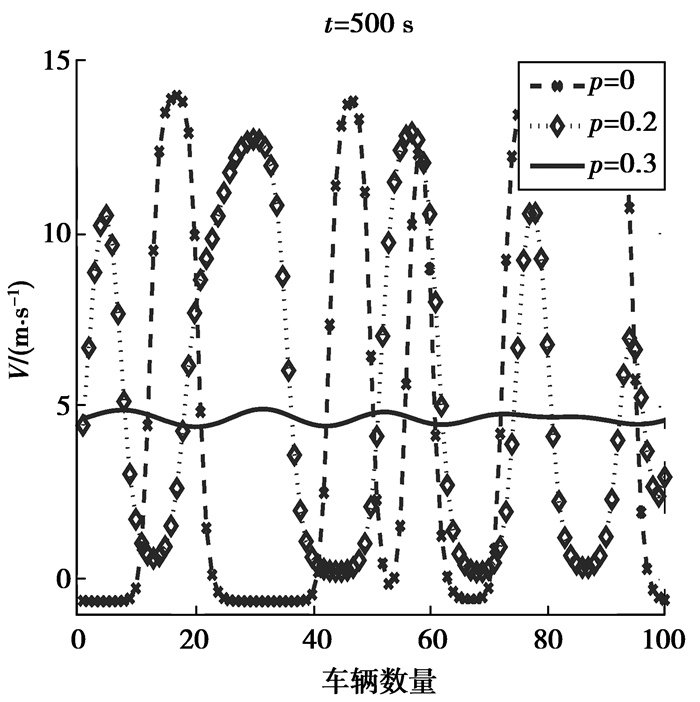
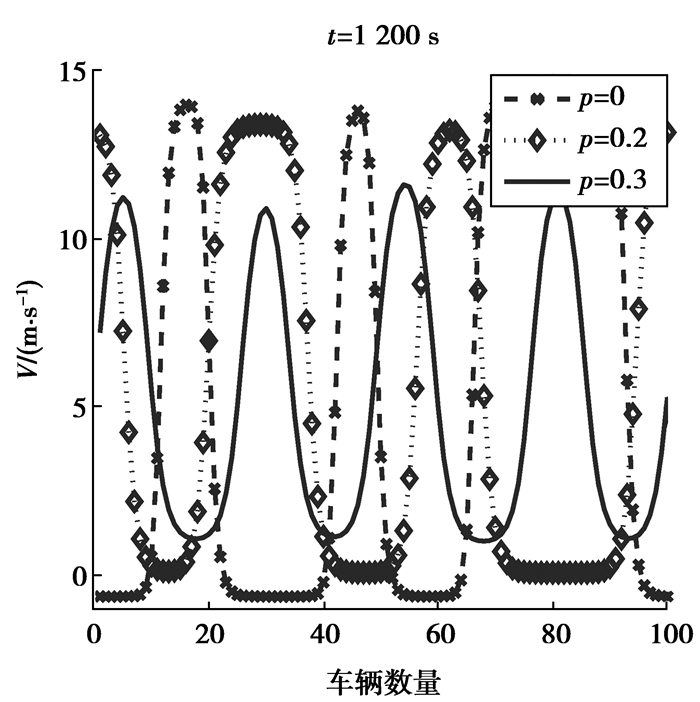
图 3和图 4为OVDA模型在t=500 s和t=1 000 s处p=0, 0.2, 0.3时的速度分布曲线图。在图中，当p=0时，OVDA模型退化成OVD模型。从模拟结果中可以得知：在OVDA模型中，初始小扰动随着车队的向后传播放大，最终引起时走时停的交通阻塞现象，但随着p值的增大，车速波动幅度不断变小，交通流的稳定性逐渐增强，从而有效地抑制交通拥堵。随着时间的推移，虽然OVDA模型的车速波动逐渐变大，但是OVDA模型中车辆的速度波动幅度还是较OVD模型的要小。这足以说明在OVDA模型中考虑了最紧邻前车的加速度信息对车流具有进一步致稳作用。

此外，通过大量模拟得到当γ=0.05时，OVD模型中出现不切实际的负速度现象。通过调节p值可以避免这个不合理的交通现象，这表明模型所做的改进是正确和合理的。

基于上述启动过程、演化过程仿真结果分析一致得到，在相同的条件下，OVDA模型的性能要优于OVD模型，即考虑最紧邻前车加速度信息对交通流起稳定作用。

4 结论

在OVD模型的基础上，考虑最紧邻前车加速度信息的作用，提出了OVDA跟驰模型。通过线性稳定性分析，OVDA模型与OVD模型对比分析表明改进模型能够进一步扩展稳定区域。仿真结果表明：与OVD模型相比，考虑最紧邻前车加速度信息的作用可使车流拥有更好的稳定特性；同时，通过调节对最紧邻前车加速度信息的关注系数，避免了OVD模型在低反应系数λ时出现的负速度现象，从而验证了模型的性能优越性和合理性。笔者提出的OVDA模型能在一定程度上再现实际的交通现象，但鉴于区域不同和路况不同，模型中参数也不尽相同，因此，下一步将采用实际交通数据对OVDA模型进行参数辨识，以进一步改进和提高模型对实际交通现象的模拟能力。