2. 重庆大学 通信工程学院, 重庆 400044;
3. 重庆市建设项目管理有限公司, 重庆 40112
2. College of Communication Engineering, Chongqing University, Chongqing 400044, P. R. China;
3. Chongqing Project Management Limited Company, Chongqing 401121, P. R. China
算术编码的发展已有几十年,早在20世纪60年代Elias就提出了算术编码的思想,1987年Witten等在文献[1]中提出了算术编码在数据压缩方面的应用,指出其比Huffman编码具有更好的压缩效率。近年来,算术编码被广泛应用到一些最新的多媒体压缩标准中,例如JPEG2000、H.264等。算术编码在压缩效率方面的优异表现来源于其将整个消息用一个[0, 1)的子区间来表示的思想,打破了传统Huffman编码等将码字和消息字符一一对应的关系。如果子区间发生改变,将会对解码输出有很大的影响;从而为其在安全性方面的设计提供了较好的基础。
虽然像DES和AES这样的基于分组加密的算法在文本加密方面能够提供较好的安全性,但将其应用到多媒体数据中却有一些明显的缺点:1)分组加密算法需要较多的计算资源,而多媒体数据量往往非常大,因此采用传统的加密方式开销很大,特别是在一些条件受限的环境中,例如无线传感器网络中,这种开销是节点无法承受的;2)因为分组加密模式是按块对数据进行处理,不适宜应用到实时多媒体传输系统中;3)很难为在空域中加密后的信号提供更好的图像处理功能,比如在变换域(离散余弦变换或小波变换)中实现的图像退化,条件访问等;4)传统的加密算法往往将图像数据看成是二进制的数据流,加密后往往会破坏图像数据的格式,可能导致解码端的异常。所以将编码和加密结合起来是当前研究的趋势。特别是基于算术编码的加密研究,得到了研究者们广泛的关注[2---------3]。在80年代末,业界还一致认为不管是静态模型或动态模型的算术编码都能提供很好的安全性[4],但是很快大家便发现单纯的算术编码并不能够提供可靠的安全性能。文献[5]中提出了对动态模型的算术编码的选择明文攻击,文献[6]中提出了另一种对静态模型的已知明文攻击和选择明文攻击。但由于算术编码良好的压缩效率,并有了初步应用,在实现过程中可以取消乘法操作等优点,其在应用中的安全性也引起了人们的重视。
文献[7]提出了一种用二值算术码实现数据加密的算法ZNJ,但很快文献[8]和[9]就给出了对ZNJ算法的改进和破解方法,其中文献[9]还针对原文献中指出该方法可以抵抗已知明文攻击,提出了对它的已知明文攻击方法。另外,Kim等人[10]提出了一种基于对连续区间进行划分的安全算术编码也在后续的研究中被攻破[11]。文献[12]提出了一种基于区间分割的二进制安全算数编码,但是后来也被证明存在一些安全漏洞[13-14]。目前公认比较安全的是Grangetto等人[15]提出的RAC (Random arithmetic coding)算法,但是该算法有一个较大的缺点,就是需要产生一串与输入符号相同长度的随机数来控制区间的置换,实际采用的是流密码的形式,它的安全性完全依赖于PRNG (Pseudo-random number generator)的安全性;如果同时密钥重用的话,会存在一些安全隐患[13-14]。
笔者提出了一种改进的基于区间置换的算术编码算法(Key-controlled interval exchanging arithmetic coding,KIEAC),并将加密结合到算术编码的过程中;同时,在编码之前利用二维Arnold混沌映射[16]对图像数据进行置乱。由于明文的冗余性是攻击加密算法的一个重要因素,所以在加密之前去除明文的冗余性是抵御统计分析的一种有效方式。而笔者提出的基于压缩编码的加密方法有效地预防了此类攻击,而且避免了RAC需要过长的随机数带来的麻烦,对输入图像数据源的置乱也进一步提升了安全性,提出的加密算法并没有影响到算术编码良好的压缩性能。
1 算术编码简介算术编码将被编码的信源符号流表示成实数域上半开区间[0, 1)中的一个数值区间,这个区间随着每个信源符号的编码而逐步减小,每次减少的程度取决于当前加入的信源符号的概率。采用固定模式编码时,假设每个信源符号的概率已知,根据这一概率分布,在[0, 1)之内,分别对每个信源符号指定一段与其相对应的数值区间,区间的大小与该符号的概率成正比。例如,设信源符号集由5个信源符号{a, b, c, d, e}组成,其出现概率和顺序如表 1所示。
| 表 1 信源符号及其范围 Table 1 Source symbols and their intervals |
假设需要进行编码的符号流为bacc。在编码开始前,对应的数值范围是整个区间[0, 1)。编码完第一个信源符号后,范围缩小到[0.2, 0.5)。然后,当编码符号a时,范围压缩到新区间的前1/5,即区间为[0.2,0.26)。如此继续下去,编码器的输出数值范围不断缩小,最终的区间为[0.236,0.238 4),则最后编码的值可为区间[0.236,0.238 4)内的任一值,设为0.236 5。而编码过程与其正好相反,首先查看最后编码的值落入哪一个信源符号所属的区间范围内,本例所示编码值0.236 5在区间[0.2, 0.5)之间,所以第一个符号为“b”;然后从编码数值中消去第一个符号“b”的影响,即减去“e”的下界值,再除以“b”对应的宽度,即(0.236 5-0.2)/0.3=0.121 6,查找这一结果落入哪个符号对应的区间范围,得到第二个符号a。重复上述步骤直到解出整个符号流为止。
通过上面的介绍简单了解了算术编码的原理,主要针对的是二元符号固定模型的算术编码进行研究,可从图 1中看出二元符号的编码过程。其解码过程也类似于多元符号模型的解码过程,通过查看落入哪个符号区间,消除已解码出的符号的影响,然后继续查表以确定被编码的是哪一个符号。
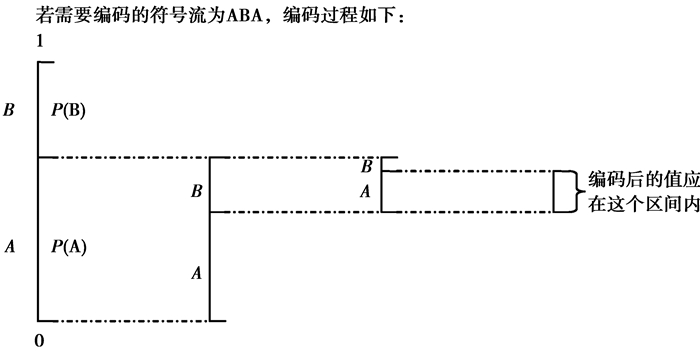
|
图 1 二元符号的算术编码过程 Figure 1 Arithmetic coding of binary symbols |
RAC算法的提出是基于算术编码的特殊性,即对压缩数据进行解码的过程对差错是非常敏感的,微小的差错会很快地扩散到整个解码流中。事实上,只要在解码过程中有一个错误,就会导致随后解码的信息没有任何的意义。这正是算术编码与Huffman编码的不同之处,Huffman编码可以在具有一定数量的错误码的基础上恢复出大部分信息,具有比较好的重同步特性;而算术编码正好相反[16],这也是设计一个具有良好鲁棒性的图像加密算法所需要的特性。研究提出的算法KIEAC也继承了这种特征。
KIEAC是通过密钥控制编码区间是否置换,以进行加密,其过程如图 2所示。在图 1中,用传统算术编码对字符串ABA进行编码,最后编码的值将落在区间I中。而从图 2中可以看出其编码区间I’与传统算术编码的编码区间I完全不同,但是I’和I的大小相等,所以区间的置换并不会影响编码的效率。
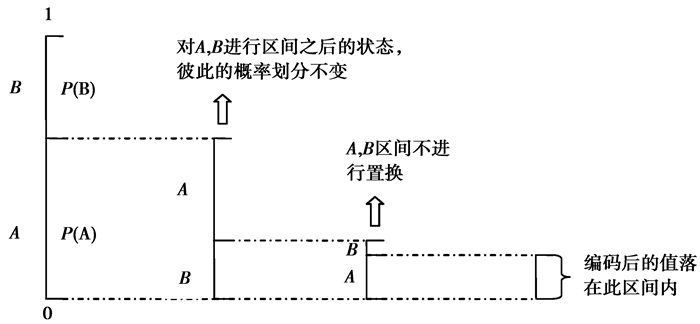
|
图 2 基于区间置乱的算术编码过程 Figure 2 Arithmetic coding based on key-controlled interval exchanging |
下面提出一种基于二元符号的区间置换规则,假设需要编码的符号集为{A,B},其概率分别为P(A)和P(B),区间排列顺序如图 1所示,加密过程如下:
1)选取密钥seed, 将其作为选定随机数发生器的种子,产生随机数r;其中r可能的取值为0, 1, …, T,其中T用于控制区间置换的间隔。随机数发生器的选取没有特殊要求,只要使得产生的随机序列具有较好的伪随机性即可。
2)如果r的值不等于0,使用标准算术编码过程对符号进行编码,然后将r的值减1;否则交换A和B在模型中的区间排列顺序再进行编码,如图 2所示,然后读取下一个随机数并赋值给r。
由于并未违反编码过程的语法,而只是对模型中的区间排列顺序进行了改变,所以并不会影响编码的效率。另一方面,解码的过程也与传统的算术编码解码过程相类似,只是需要密钥的控制才能解密出源消息。解密过程如下,
1)选取与加密端相同的密钥seed和随机数发生器,生成随机数r,即生成解密密钥流。
2)如果r的值不等于0,使用标准算术解码器进行解码,然后将r的值减1;否则交换A和B在模型中的区间排列顺序再进行解码。然后读取下一个随机数并赋值给r。
可以从中看出KIEAC是完全可逆的。
2.2 图像加密应用为了进一步提高算法的安全性,在对图像进行编码之前引入了置乱技术,采用二维Baker混沌变换对输入图像进行置乱。二维Baker映射的初始定义为[17]
| $ B\left( {x,y} \right) = \left\{ {\begin{array}{*{20}{c}} {\left( {2x,y/2} \right),}&{0 \le x < 1/2,}\\ {\left( {2x - 1,y/2 + 1/2} \right),}&{1/2 \le x \le 1,} \end{array}} \right. $ |
该映射的作用是将面积为1的单位正方形的左右子区间进行压缩和拉伸,可以稍对其做变化后用来对输入明文图像进行像素置乱。可以将[0, N]区间化分为k个子区间,对每个子区间做类似的变换,广义的离散化二维Baker映射,即
| $ {B_{\left( {n1, \cdots ,nk} \right)}}\left( {x,y} \right) = \left( {\frac{N}{{{n_i}}}\left( {x - {N_i}} \right) + y\bmod \frac{N}{{{n_i}}},\frac{{{n_i}}}{N}\left( {y - y\bmod \frac{N}{{{n_i}}}} \right) + {N_i}} \right), $ |
其中:i=1, 2, …, k;N是图像的尺寸,(x, y)∈{0, 1, …, N-1}。由k个整数所构成的序列n1, n2, …, nk满足:n1+n2+…+nk=N,且每一个整数ni可以整除N。
从上述公式可知Baker映射是一个保面积的映射,同时也是一个一一映射,方阵内的每一点唯一地变换到方阵内的另一点,具有非常典型的产生混沌运动的2个因素:拉伸和折叠。考虑到Baker映射良好的混沌特性,以及理想加密系统所需的扩散和混淆要求,将其用于图像置乱处理是比较好的选择。
在提出的图像加密系统中,首先对图像数据进行预处理,用Baker映射对图像像素位置进行若干轮变换,即把图像看作一个矩阵,通过改变像素坐标而改变图像灰度值的布局,经过变换后的图像会变得非常混乱。此时将已置乱的十进制像素值转换为八位二进制,再利用提出的KIEAC算法对其进行编码压缩及加密。解密时只需将正确解码的序列用Baker的逆矩阵对其进行相同轮数的逆变换,再将此得到的结果转换为十进制恢复图像数据。
3 实验结果及分析 3.1 加密效果为了验证KIEAC算法的正确性和加密效果,选择512×512的灰度图像peppers作为输入明文,T=4。实验效果如下图 3所示

|
图 3 加密效果图 Figure 3 Encryption result |
图 3(a)显示的是明文图片,图 3(b)显示的是对应密文图片。可以看到,密文图片呈随机噪声分布,没有泄露任何明文图片的信息,输入正确密钥后算法能够恢复出明文图片。
3.2 密文均衡性分析一个好的加密算法所得到的密文中0和1的分布应该比较均匀,即达到0,1分布的均衡。在试验中,分别采用10幅不同的明文在相同的密钥下进行加密,分别分析其得到的密文中0和1所占的百分比,然后计算他们的平均值,结果如表 2所示。从表 2可以看出密文中0和1的比例都在50%左右,具有较好的均衡性,即算法有很好的加密效果。
| 表 2 0, 1均衡性测试结果 Table 2 Test result of 0/1 balance |
明文敏感性是为了保证明文发生微小的改变时所得到的密文有较大变化。可以利用NPCR[18]来衡量明文的敏感性,其计算公式为
| $ {\rm{NPCR = }}\frac{{\sum\limits_i {D\left( i \right)} }}{{{\rm{size}}\left( {\rm{D}} \right)}} \times 100\% , $ |
其中,
| $ D\left( i \right) = \left\{ \begin{array}{l} 0,\;\;\;{C_1}\left( i \right) = {C_2}\left( i \right),\\ 1,\;\;\;{C_1}\left( i \right) \ne {C_2}\left( i \right), \end{array} \right. $ |
C1(i),C2(i)为位置i处的密文像素值。
通过对不同的明文图像,以及改变其中一位bit所得到的图像,用KIEAC算法进行加密,计算所得到的NPCR如表 3所示。可以发现NPCR的值都大于98%,表明该加密算法对明文的微小的变化都非常敏感。
| 表 3 明文敏感性测试 Table 3 Test results of plaintext sensitivity |
密钥敏感性可以保证密钥发生细小改变时对加密算法的输出产生较大影响。在实验中保持相同的明文输入图像,改变密钥的一个bit,然后分析密文图像的改变。通过实验发现密文数据的平均改变率达到98.6%以上。同时,为了说明密钥改变对密文图像解密的影响,改变加密密钥的一个bit,然后对图 3中所得的密文图像进行解密,得到的解密图像如图 4(a)所示。可以看到密钥即使发生细微的改变,所解密得到的明文将会变得截然不同;而且无法从解密后的图像获得任何关于原文图像的有用信息。
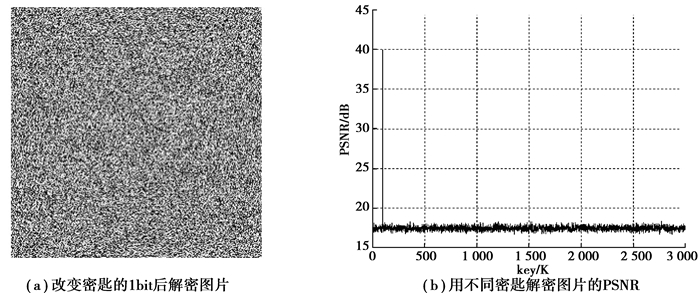
|
图 4 密钥敏感性测试结果 Figure 4 Test result of key sensitivity |
为了进一步说明算法对密钥的敏感性,随机产生3 000个解密密钥(其中包含正确的解密密钥),利用这些密钥分别对密文图片进行解密,然后计算解密图片的PSNR,如图 4(b)所示。发现除了正确密钥以外,其他密钥解密所得的解密图片的PSNR都非常小;这也进一步说明了该算法对密钥改变具有良好的敏感性。
3.5 效率分析研究所提出的KIEAC算法利用随机数发生器产生加密密钥流,本质上类似于流密码算法。但是跟RAC不同的是,所需要的密钥流长度小于明文的长度。具体而言,对于长度为L的明文,由于每次产生的随机数取值范围在[0, T]之间,假设其平均值为T/2,则所需密钥流的平均长度为2L/T。而在相同的明文长度下,RAC所需的密钥长度为L。因此,在相同的条件下(即假设采用相同的随机数发生器),加密效率是RAC的T/2倍。
但是需要说明的是,虽然T的取值越大,加密效率越高,但是T的取值过大会削弱安全性。因此,在实际的应用中,需要根据安全强度的要求和加密效率的要求选择一个合适的T的取值。
4 结论提出了一种基于随机区间置换的安全算术编码KIEAC,并结合二维Baker映射将其应用在图像加密中。该算法首先对图像的像素值进行置乱,利用算术编码对模型的敏感性,通过密钥控制编码区间的顺序对输入符号进行压缩加密。本算法不仅保留了RAC算法的优点,而且克服了其密钥流需要和明文符号长度一致的缺点。最后的实验和安全性分析结果表明:该加密算法具有较好的加密效果,对明文和密钥都非常敏感,因此对多种攻击手段都具有良好的免疫性;同时算法比RAC具有更好的加密效率。既适用于软件加密系统,而且很容易移植到硬件平台上, 具有良好的应用前景。
| [1] | Witten H, Radford M N, John G C, et al. Arithmetic coding for data compression[J]. Communications of the ACM, 1987, 30(6): 520–540. DOI:10.1145/214762.214771 |
| [2] | Pande A, Mohapatra P, Zambren J, et al. Securing multimedia content using joint compression and encryp-tion[J]. IEEE Multimedia, 2013, 20(4): 50–61. DOI:10.1109/MMUL.2012.29 |
| [3] | Lin Q Z, Wong K W, Chen J Y. An enhanced variable-length arithmetic coding and encryption scheme using chaotic map[J]. The Journal of Systems and Software, 2013, 86(5): 1384–1389. DOI:10.1016/j.jss.2013.01.012 |
| [4] | Witten I H, Cleary J G. On the privacy afforded by adaptive text compression[J]. Computers & Security, 1988, 7(4): 397–408. |
| [5] | Bergen H A, Hogan J M. Data security in a fixed-model arithmetic coding compression algorithm[J]. Computers & Security, 1992, 11(5): 445–461. |
| [6] | Bergen H A, Hogan J M. A chosen plaintext attack on an adaptive arithmetic coding compression algorithm[J]. Computers & Security, 1993, 12(2): 157–167. |
| [7] |
赵风光, 倪兴芳, 姜峰, 等.
算术编码与数据加密[J]. 通信学报, 1999, 20(4): 92–96.
Zhao fengguang, Ni Xingfang, Jiang Feng, et al. Arithmetic coding and data encryption[J]. Journal of China Institute of Communications, 1999, 20(4): 92–96. (in Chinese) |
| [8] |
谢冬青, 谢志坚, 李超, 等.
关于一种算术编码数据加密方案的密码分析[J]. 通信学报, 2001, 22(3): 41–45.
Xie Dongqing, Xie Zhijian, Li Chao, et al. Cryptanalysis of data eneryption scheme based on arithmetic coding[J]. Journal of China Institute of Communications, 2001, 22(3): 41–45. (in Chinese) |
| [9] |
郑浩然, 金晨辉.
对基于算术编码的一个数据加密算法的已知明文攻击[J]. 通信学报, 2003, 24(11): 73–78.
Zheng Haoran, Jin Chenhui. An attack with known plaintexts to an eneryption algorithm[J]. Journal of China institute of Communications, 2003, 24(11): 73–78. (in Chinese) |
| [10] | Kim H J, Wen J T, Villasenor J D. Secure arithmetic coding[J]. IEEE Transactions on Signal Processing, 2007, 55(5): 2263–2272. DOI:10.1109/TSP.2007.892710 |
| [11] | Jakimoski G, Subbalakshmi K P. Cryptanalysis of some multimedia encryption schemes[J]. IEEE Transactions on Multimedia, 2008, 10(3): 330–338. DOI:10.1109/TMM.2008.917355 |
| [12] | Wen J T, Kim H J, Villasenor J D. Binary arithmetic coding with key-based interval splitting[J]. IEEE Signal Processing Letters, 2006, 13(2): 69–72. DOI:10.1109/LSP.2005.861589 |
| [13] | Katti R S, Srinivasan S K, Vosoughi A. On the security of randomized arithmetic codes against ciphertext-only attacks[J]. IEEE Transactions on Information Forensics and Security, 2011, 6(1): 19–27. DOI:10.1109/TIFS.2010.2096809 |
| [14] | Rajendra S. Katti, Aida Vosoughi. On the security of key-based interval splitting arithmetic coding with respect to message indistinguishability[J]. IEEE Transactions on Information Forensics and Security, 2011, 7(3): 895–903. |
| [15] | Marco G, Enrico M, Gabriella O. Multimedia selective encryption by means of randomized arithmetic Coding[J]. IEEE Transactions on Multimedia, 2006, 8(5): 905–917. DOI:10.1109/TMM.2006.879919 |
| [16] | Peter W M, Wu X L. Resynchronization properties of arithmetic coding[C]// 1999 International Conference on Image Processing (ICIP99), [s. n.]:IEEE, 1999, 2: 545-549. |
| [17] | Fridrich J. Symmetric ciphers based on two-dimensional chaotic maps[J]. International Journal of Bifurcation and Chaos, 1998, 8(6): 1259–1284. DOI:10.1142/S021812749800098X |
| [18] | Pareek N K, Patidar V, Sud K K. Image encryption using chaotic logistic map[J]. Image and Vision Computing, 2006, 24: 926–93. DOI:10.1016/j.imavis.2006.02.021 |
 2015, Vol. 38
2015, Vol. 38

