舞动是指导线在风力及(或)不对称覆冰作用下引起的低频率、大幅度的自激振动，是一种空气动力失稳现象^{[1, 2]}。舞动多发生在冬季，其能量很大，且持续时间长，易对输电线路造成机械损坏和电气故障，轻则引起相间闪络、损伤导线、地线及金具等，重则导致断股、断线、甚至倒塔等恶劣事故，严重威胁着输电线路的安全稳定运行^{[3, 4]}。运行观测和统计资料表明，中国是舞动灾害最严重的国家之一^{[5, 6]}。随着中国电网规模的发展和恶劣天气的频繁出现，输电线舞动事故的发生频率和危害程度均有明显的增加，且舞动区域已不仅局限在少数范围内，也遍及到国家电网的大部分地区^[7]。因此，对输电线路舞动及其预防措施的研究具有重要的理论意义和工程实用价值。

近年来，国内外学者对导线舞动激发机理、计算仿真及导线防舞动措施等进行了多方面的研究，取得了很多重要成果并应用于实际工程。遗憾的是，由于输电线和气流相互作用所造成的耦合以及输电线的大幅运动所造成的几何非线性等，使舞动问题变得十分复杂，迄今为止尚无统一、普适的输电线舞动激发理论。目前具有代表性的主要有4种^[8]，分别为Hartog^[9]提出的横向起舞机理、Nigol等^[10]提出的扭转振动起舞机理、Yu等^[11]提出的偏心惯性耦合起舞机理及中国学者尤传永^[12]提出的动力失稳起舞机理。

现行的防舞措施概括起来可分为3大类^[13]：一是从气象条件考虑，避开易于形成舞动的覆冰区域与线路走向；二是从机械与电气的角度，设计提高线路系统的抗舞动能力；三是采取各种防舞装置，抑制舞动的发生。但值得注意的是：其一，考虑到节省线路走廊的经济性设计要求以及施工便宜性等因素，使得部分输电线路是无法完全避开舞动区的；其二，在实际应用中，加强输电线路质量的技术及相关的抗舞设计尚不够详实和规范，经济性以及可操作性较差，同时也缺乏实践经验；其三，防舞器是基于不同舞动机理开发得到的，导致目前应用较多的几种防舞装置都具有其明显的设计特点和应用局限性，防舞效果也存在很大差异^[7]。显然，要想完全制服舞动还需很长一段时间的努力，而目前迫切需要一种主动性更强、应用范围更广的输电线防舞动辅助决策方法，来减轻输电系统遭受的舞动灾害。

一方面，气象条件是影响舞动激发的最重要因素，只要满足舞动条件，各区域、各电压等级的输电线均可能发生舞动^[14]；另一方面，近年来输电线舞动在线监测装置和方法得到了蓬勃发展^{[15, 16]}，而舞动在线监测系统的成功运行为研究导线舞动积累了宝贵的气象资料。因此，为了弥补现有防舞措施的不足，加强输电线路的防舞能力，笔者在分析影响舞动的环境气象因素基础上，提出一种基于Adaboost学习算法的输电线舞动气象预警模型。预警结果可为电网运维人员提供决策支撑，提前做好有针对性的抗风、除融冰等防舞措施，避免防范不足引起事故及过度防范浪费资源，保障输电线路的安全稳定运行。

导线舞动是一种复杂的流固耦合振动，其形成因素很多，经过多年来国内外学者对舞动的研究，归纳得出了引起舞动的3个重要因素^{[2, 5, 7]}。

1)导线覆冰：引起导线舞动的决定性因素。导线上要形成覆冰，必须具备3个条件：一是空气湿度较大，一般在85%以上；二是合适的温度，一般为0~-5 ℃；三是可使空气中水滴运动的合适风速，一般为1~15 m/s。

2)风的激励：导线舞动的直接原因。一段线路的舞动状态及其强弱，除了与风速大小有关外，还取决于风向对导线轴线(线路走向)的夹角。

3)线路结构与参数：引起舞动的内因。不合理的线路结构参数组合易引起舞动，这些因素主要包括：导线的类型、导线截面积、线路档距等。

综上可见，导线舞动的形成与外界气象环境密不可分，这些气象条件包括：风速、风向对导线轴线夹角、温度和相对湿度。引起导线舞动的内因是线路结构与参数，而当内因相对不变时，事物的变化由外因决定。因此，笔者结合文献[17]给出的舞动导线参数的相关资料，对引起导线舞动的内因(导线结构、导线截面和档距)按表 1所示进行划分，然后据此将线路历史舞动资料进行归类，得到共计18类线路(如：单导线、小截面、小档距)的舞动情况统计数据，在此基础上建立输电线舞动的气象预警模型。

表1(Table 1)

表1 导线舞动内因分类统计表Table 1 Classification of galloping internal cause 内因 导线结构 导线截面 S/mm 档距 L/m 分类 单导线 小 ( S≤150) 小 (L≤300) 分裂导线 中 (150＜S≤300) 中 (300＜L≤600) — 大 (S＞300) 大 (L＞600)

表1 导线舞动内因分类统计表 Table 1 Classification of galloping internal cause

由于高度的变化对风速有影响，而气象站观测得到的风速以及气象预报风速一般是默认为离地10 m高的风速，因此，应按式(1)统一折算至导线高度处的风速v_l^[18]。

由于输电线舞动的物理模型不够精确，且模型中的部分参量在实际线路上难以通过测量获取，导致利用物理模型进行舞动预警的实用性和准确性较低。但是，由于对总体起作用的环境和条件的变化必然影响着每一个个体，因此，受动力学规律支配的单个客体的行为只能在一定范围内偏离总的方向，且它们在总体上仍表现出统计的必然性^[19]。因此，统计学习理论是面对数据而又缺乏理论模型时最基本的分析手段。

机器学习基于以往的观察来获取较准确的预测，它提供了一种从观测数据出发得到目前尚不能通过原理分析得到的规律，进而利用这些规律预测未来数据的方法，其核心任务是把样例分类到各可能的离散值对应的类别中，并对未知样本做出尽可能精确的预测^[20]。

综上所述，输电线舞动预警问题可归结为有监督学习下的分类预测问题：对照实际输电线路情况和表 1，选择18种线路类型中与之对应的一类，以该类线路的历史舞动情况统计数据(风速、风向对导线轴线夹角、温度和相对湿度)构成训练样本集，以下述的Adaboost集成学习算法形成分类学习器，并根据气象预报数据进行导线舞动预警。

对一个预测分类问题，统计学习的基本目标是根据观测数据建立具有较强泛化能力的学习器。但在很多情况下，由于学习器的精确性受领域知识和训练数据及其分布(尤其是对那些还未完全了解其本质的预测问题，如导线覆冰舞动)的影响很大，使得很难直接构造具有高精度的学习器。然而，产生数个只比随机猜测略好的弱学习器却很容易，因此，寻找一般的提高已有学习器精确性的方法是很有价值的，这在直接构造强学习器非常困难的情况下，为学习算法的设计提供了一种有效的新思路和新方法，集成学习正是在这一背景下应运而生的^[21]。

自集成学习的概念被提出以来，其在很多领域得到了快速的发展和广泛的应用。目前常用的集成学习算法有Bagging算法(bootstrap aggregation自助聚集法)和Boosting算法(增强法)，Boosting算法中最流行的一种就是Adaboost(adaptive boosting自适应增强)算法。

Adaboost算法建立在Schapire的关于“弱分类器”的性能分析及Freund的关于“学习理论”的早期研究基础上于1996年被提出。由于该算法不要求事先知道弱学习算法预测精度的下限，只要求基本分类器的正确识别率略大于“随机猜想”即可(也被称为弱分类器)，因此，能够更好地适用于实际问题^[22]。它具有泛化错误率低、易编码等优点，被评为数据挖掘十大算法之一。

Adaboost算法的基本思想是利用大量的分类能力一般的弱分类器通过一定方法叠加起来，构成一个分类能力很强的强分类器^[23]。

Adaboost算法描述如下：

输入：弱分类器设计方法C；训练次数(弱分类器个数)T；样本集X={(x₁,y₁),(x₂,y₂),…,(x_N,y_N)}。其中，x_i为第i个样本的气象特征向量；y_i={-1,1}表示第i个样本的类别标号：-1表示未发生舞动，1表示有发生舞动；N为样本数。

初始化：样本权值分布w₁(i)=1/N，i=1,2,…,N。

当t=1,2,…,T时：

1)根据w_t(i)从X中进行有放回的抽样生成新的样本集合X_t。

2)在X_t上训练弱分类器C_t(X)，并用C_t(X)对原始训练样本集X进行分类。

3)计算C_t(X)的分类错误率。

4)计算C_t(X)的系数。

5)更新权值分布。

式中：${{Z}_{t}}=\sum\limits_{i=1}^{N}{{{\omega }_{t}}\left( i \right)}\cdot {{e}^{-{{a}_{t}}}}^{{{y}_{i}}{{C}_{t}}\left( {{x}_{i}} \right)}$是归一化因子，可使得$\sum\limits_{i=1}^{N}{{{\omega }_{t+1}}\left( i \right)}=1$。

6)最终分类器。

作为弱分类器，简单分类器的效果更好，因此，笔者选择最常用的单层决策树作为弱分类器。该决策树仅基于单个输入特征并采用阈值划分方法来做决策，即只有一个节点，且由于这棵树只有一次分裂过程，与树桩形似，因此，它也被称作决策桩(decision stump)^[24]。

决策桩构造的最关键问题是如何判断阈值划分结果的好坏，以便选择最佳分割点。目前，一般采用基于信息量或错误率(如Gini指标)的衡量准则，而文献[25]指出：Gini不纯度指标比信息量指标性能更好，且计算方便，其最大的特点是计算时只需考虑类值在被划分时每一部分的分布情况。因此，笔者采用Gini指标来评估分割规则的优劣程度，对于包含c个类别的数据集S，其定义^{[26, 27]}如下：

对于一个数值型属性，基于Gini指数的决策桩分割思想是：在遍历所有可能的分割方法后，选择使评估值Gini(S,rule)达到最小的作为此节点处的最优划分规则^[28]。其流程描述为

1) 对数值型属性的样本值进行排序，假设排序后的结果是(x₁,y₁)，(x₂,y₂)，…，(x_n,y_n)。

2) 由于分割只发生在2个数据点间，因此，通常取中点(x_i+x_i+1)/2作为分割点，然后从小到大依次取不同的分割点，并计算各分割规则的Gini值。

3) 取使Gini值最小的点作为最佳分割点。

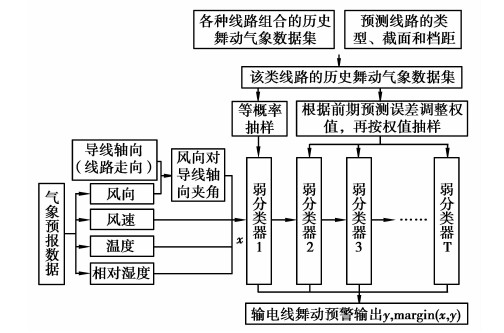
笔者提出的基于Adaboost方法的输电线舞动预警的流程如图 1所示。

图1(Figure 1)

图1 输电线舞动预警流程图 Fig. 1 Flow chart of early warning for transmission line galloping

对由气象预报输入向量x所得的输电线舞动预测结果y，可用式(8)计算其置信度：

最后，根据舞动预测结果的margin值，暂按表 2所示设定输电线舞动的预警等级。

表2(Table 2)

表2 输电线舞动预警等级表Table 2 Early warning levels of transmission line galloping 条件 预警等级 margin＞0.7 Ⅰ级 0.4＜margin≤0.7 Ⅱ级 0.1＜margin≤0.4 Ⅲ级

表2 输电线舞动预警等级表 Table 2 Early warning levels of transmission line galloping

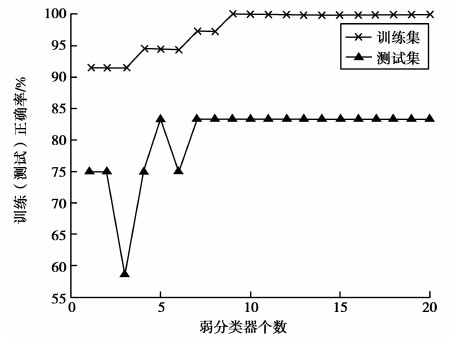
以河南省电力公司及其“输电线路舞动防治技术”国网重点实验室统计的近3年来110 kV及以上电压等级输电线路覆冰舞动调查情况为例，根据其中类型为220 kV电压等级、双分裂、大截面(S>300)导线(由于记录数据缺乏线路的具体档距，因此，这里暂不分档距大小)的舞动情况，利用Matlab 7.6.0 工具对笔者所述方法的分类结果进行编程验证。具体为选取导线出现覆冰情况下的其中“25(舞动)+10(未舞动，指疑似发生舞动但巡线并未发现任何损害)”组数据构成训练集，“7(舞动)+5(未舞动)”组数据构成测试集。验证结果如图 2所示，方法与其他常用分类算法的效果对比见表 3。

图2(Figure 2)

图2 文中方法对输电线舞动预测分类效果图 Fig. 2 Effect of classification of transmission line galloping using Adaboost method

表3(Table 3)

表3 不同分类算法的效果对比Table 3 Comparison of different classification methods % 算法 Adaboost学习算法 Logstic回归算法 单层决策树算法 训练集正确率 100.00 91.43 91.43 测试集正确率 83.33 75.00 75.00

表3 不同分类算法的效果对比 Table 3 Comparison of different classification methods

由图 2和表 3可以看出，所述方法在河南省220 kV大截面分裂导线舞动样本训练集和测试集上都表现出较好的稳定性和较高的正确率，分别达到100.00%和83.3%，与其他常用分类方法相比都有所提高，适用于输电线路舞动预警。

笔者还采用Adaboost学习算法的置信度来近似舞动发生的概率，并据此进行预警。由表 4可以看出：①测试集中分类错误的第9、12两组数据的置信度均较小(0.191 1和0.376 2)，但是某些分类正确的数据组(如第3、10、11组)的置信度有可能更小；②就现有结果来看，置信度大于40%的数据均分类正确(这也是本文按表 2所示设定预警等级的重要依据)。因此，该值可作为划分处理预警目标优先度的参考标准。

表4(Table 4)

表4 测试集上的分类置信度Table 4 Classification confidence of test set 序号 1 2 3 4 5 6 7 8 9 10 11 12 实际分类 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 学习分类 1 1 1 1 1 1 1 -1 1 -1 -1 1 置信度 0.376 2 0.376 2 0.191 9 0.519 9 0.750 5 0.750 5 0.750 5 -0.589 3 0.191 1* -0.133 4 -0.133 4 0.376 2* 注：加*是指该次预测分类错误(实际是-1的却被分类为1)。

表4 测试集上的分类置信度 Table 4 Classification confidence of test set

笔者提出将输电线舞动预警问题归结为有监督学习下的分类预测问题的总体思路和提出以引发线路舞动的气象环境因素的预报值为输入，以Adaboost集成学习法作为分类器算法进行导线舞动预警的技术方法都是科学和有效的。对置信度大于40%的Ⅰ、Ⅱ级舞动预警线路应重点防控、加强巡视监测、做好调度应急预案；同时，对置信度较小的Ⅲ级舞动预警也不可掉以轻心，应做好充分准备，尽力将输电线路舞动的损害降至最低。值得注意的是，输电线路舞动的发生是线路系统能量不断积累的过程，因此，除了用具体时刻的温度、风速等气象参数描述线路舞动时的外部环境信息，还应加入刻画积累过程的物理量，如持续时间、覆冰厚度等，这也是下一步研究的方向。