2. 哈尔滨电工仪表研究所, 哈尔滨 150028
2. Harbin Research Institute of Electrical Instrument, Harbin 150028, P. R. China
木材干燥过程是木材加工处理中的重要组成部分,通过使用先进的干燥设备和干燥技术不仅可以节约大量的森林资源,提高木材的加工品质,还可以获得环保和节能的效果。木材含水率是木材干燥过程中重要的技术指标[1]。木材含水率的常用测量方法有很多,包括称重法、电导法、电容法、微波法等。传统的测量方法是称重法,可以获得准确的木材含水率数据,但是测量时间长且受人为因素影响较大。电导法是根据木材中水分的导电性能,测量两电极间的电阻值,间接测量木材含水率,但是电导法只能测量电极附近的局部含水率。电容法和微波法是通过木材含水率同电磁微波的关系进行测量,但是测量范围有限且受木材干燥窑内温度和湿度影响较大,能耗较高[2, 3, 4]。
软测量技术是一种新型测量方法,是建立待测变量与可测或者易测过程变量之间的非线性函数关系,间接得到待测变量的估计值[5, 6]。最小二乘支持向量机(least squares support vector machines,LS-SVM)是基于统计学习理论的标准支持向量机(support vector machines,SVM)的改进和扩展,它能够拟合非线性函数,将SVM的二次规划问题转变成求解线性方程,提高了求解速度[7, 8, 9]。LS-SVM的惩罚因子和核函数参数对软测量模型的准确度和泛化能力都有一定影响,有必要进行优化选择。针对木材干燥过程具有强耦合、大滞后、非线性的特点,提出用LS-SVM建立木材含水率的软测量模型,并利用粒子群优化算法(particle swarm optimization,PSO)选择软测量模型的最优参数。将PSO优化的LS-SVM方法运用在木材干燥的非线性系统上,通过实际测量的木材干燥窑内温度、湿度以及对应的木材含水率值建立模型,实现木材含水率的软测量。
1 粒子群优化的最小二乘支持向量机 1.1 最小二乘支持向量机回归算法最小二乘支持向量机是标准支持向量机方法的一种改进。该方法将标准支持向量机中的不等式约束条件变为等式约束条件,将损失函数作为训练样本的经验损失,同时,把求解二次规划问题转变成求解线性方程组问题[10, 11]。在求解问题上,最小二乘支持向量机相比标准支持向量机,有更好的收敛速度和精度。
设训练样本集S={(xi,yi),i=1,2,…,l},xi∈Rn是输入数据,yi∈R是输出数据,LS-SVM原理如下
| $\left\{ \begin{gathered} \mathop {\min }\limits_{\omega ,b,e} J\left( {\omega ,e} \right) = \frac{1}{2}{\left\| \omega \right\|^2} + \frac{1}{2}c\sum\limits_{i = 1}^l {e_i^2} ,\hfill \\ {\text{s}}{\text{.t}}{\text{.}}{y_i} = {\omega ^T}\varphi \left( {{x_i}} \right) + b + {e_i},i = 1,2,\cdots ,l \hfill \\ \end{gathered} \right.$ | (1) |
上述优化函数式(1),对应的Lagrange函数为
| $L\left( {\omega ,b,e,a} \right) = J\left( {\omega ,e} \right) - \sum\limits_{i = 1}^l {{\alpha _i}\left[{{\omega ^T}\varphi \left( {{x_i}} \right) + b + {e_i} - {y_i}} \right]} $ | (2) |
对式(2)进行优化,得
| $\left\{ \begin{gathered} \frac{{\partial L}}{{\partial \omega }} = 0 \Rightarrow \omega = \sum\limits_{i = 1}^l {{\alpha _i}\varphi \left( {{x_i}} \right)} ,\hfill \\ \frac{{\partial L}}{{\partial b}} = 0 \Rightarrow \sum\limits_{i = 1}^l {{\alpha _i} = 0} \hfill \\ \frac{{\partial L}}{{\partial {e_i}}} = 0 \Rightarrow {\alpha _i} = \gamma {e_i},i = 1,2,\cdots ,l \hfill \\ \frac{{\partial L}}{{\partial {\alpha _i}}} = 0 \Rightarrow {\omega ^T}\varphi \left( {{x_i}} \right) + b + {e_i} - {y_i} = 0,i = 1,2,\cdots ,l \hfill \\ \end{gathered} \right.$ | (3) |
| $\left[\begin{gathered} 0{\text{ }}1 \hfill \\ 1{\text{ }}\Omega + {\gamma ^{ - 1}} \hfill \\ \end{gathered} \right]\left[\begin{gathered} b \hfill \\ a \hfill \\ \end{gathered} \right] = \left[\begin{gathered} 0 \hfill \\ y \hfill \\ \end{gathered} \right]$ | (4) |
| $\Omega = {\left\{ {{\Omega _{ij}}} \right\}_{l \times l}},{\Omega _{ij}} = {\varphi ^T}\left( {{x_j}} \right)\varphi \left( {{x_i}} \right) = K\left( {{x_j}{x_i}} \right)$ | (5) |
| $y\left( x \right) = \sum\limits_{i = 1}^l {{\alpha _i}K\left( {x,{x_i}} \right)} + b$ | (6) |
PSO算法初始化为一群随机粒子,并追随当前最优粒子进行不间断的迭代搜索直至找到最优解[13]。在每一次迭代过程中,PSO主要通过跟踪个体极值pbest和全局极值gbest来更新各个粒子。个体极值是目前粒子本身所找到的最优解,而全局极值则是整个种群目前所找到的最优解[14, 15, 16]。
设粒子群的种群规模为M,决策空间n维,粒子i在t时刻的坐标位置是Xit=(xi1t,xi2t,…,xint),i=1,2,…,M,粒子i的速度,即每次迭代中粒子移动的距离,用Vit=(vi1t,vi2t,…,vint)表示,那么粒子i在t时刻的第j(j=1,2,…,n)维子空间中的飞行速度和位置可由下式调整
| $v_{ij}^t = \omega v_{ij}^{t - 1} + {c_1}{r_1}\left( {{p_{ij}} - x_{ij}^{t - 1}} \right) + {c_2}{r_2}\left( {{g_j} - x_{ij}^{t - 1}} \right)$ | (7) |
| $v_{ij}^t = \left\{ \begin{gathered} {v_{\max }},v_{ij}^t{\text{ > }}{v_{\max }} \hfill \\ - {v_{\max }},v_{ij}^t{\text{ < - }}{v_{\max }} \hfill \\ \end{gathered} \right.$ | (8) |
| $x_{ij}^t = x_{ij}^{t - 1} + v_{ij}^t$ | (9) |
式(7)表示粒子的飞行速度与前一时刻飞行速度、惯性权值、个体和种群认知以及随机数之间的关系;式(8)是用来限制粒子的飞行速度;式(9)表示粒子飞行所处的位置。
1.3 基于PSO算法的LS-SVM参数寻优LS-SVM模型中的惩罚因子c对LS-SVM的经验误差和推广能力有很大影响。LS-SVM选用不同的核函数可以构造不同的支持向量机,常用的核函数有多项式核函数、径向基核函数和Sigmoid核函数等。其中,径向基核函数是目前使用最广泛的核函数,本研究在建模时选择径向基函数作为核函数,其形式如下
| $K\left( {{x_i},{y_i}} \right) = \exp \left( { - \gamma {x_i} - x_j^2} \right),\gamma {\text{ > }}0$ | (10) |
惩罚因子c和核函数参数γ共同影响LS-SVM模型的性能,因此,是否选择最优的参数c和γ对软测量模型的准确度有很大影响。利用PSO算法对惩罚因子c和核函数参数γ进行寻优。
2 基于PSO-LSSVM的木材含水率软测量模型 2.1 木材含水率软测量模型结构在木材干燥过程中,木材含水率的下降主要是受木材干燥窑内的温度和湿度影响。通过PSO优化的LS-SVM建模方法建立干燥过程木材含水率的软测量模型,也就是木材干燥窑内温度、湿度以及木材含水率之间的模型。
研究选择的实验树种是水曲柳,利用软测量建模方法对水曲柳干燥过程的木材含水率进行建模。实验所用的木材含水率实际值是通过木材含水率检测仪,由电导法测量获得。利用均方根误差(RMSE)来描述模型的预测误差,RMSE计算方法如式(11)所示。
| ${\text{RMSE = }}\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{X_i} - {Y_i}} \right)}^2}} }$ | (11) |
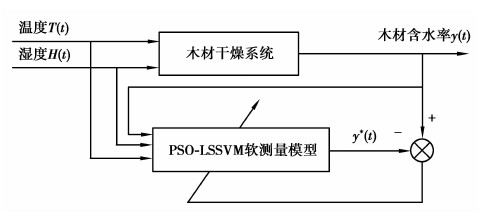
使用MATLAB R2010a仿真软件作为仿真环境。木材干燥窑的软测量模型包括干燥窑内的温度、湿度以及木材含水率,建立的基于PSO优化的LS-SVM的干燥过程木材含水率软测量模型结构如图 1所示。
|
图1 干燥过程木材含水率软测量模型结构 Fig. 1 Wood moisture content soft sensor model of wood drying process |
木材干燥系统是一个动态系统,当前状态的木材含水率不仅和外部环境的温度和湿度有关,也和前一状态的木材含水率变化有关。因此,研究将木材干燥全过程的含水率变化看成是一个具有可控外部干预和非线性递减的时间序列。木材干燥过程的软测量模型包括干燥窑内的温度、湿度以及木材含水率。其中,木材干燥窑的温度T(t)和湿度H(t)是系统的输入量,木材含水率y(t)是系统的输出量,y*(t)为PSO-LSSVM模型当前的输出值。木材干燥系统当前温度的输入是T(t),系统历史状态的温度输入是T(t-1)…T(t-p);木材干燥系统当前湿度的输入是H(t),系统历史状态的湿度输入是H(t-1)…H(t-p);木材干燥系统当前的木材含水率输出是y(t),系统历史状态的木材含水率输出是y(t-1)...y(t-q);PSO-LSSVM的木材干燥过程软测量模型结构关系如式(12)所示。
| ${y^ * }\left( t \right) = f\left[{T\left( t \right),\cdots ,T\left( {t - p} \right),H\left( t \right),\cdots ,H\left( {t - p} \right),y\left( {t - 1} \right),\cdots ,y\left( {t - q} \right),\theta } \right]$ | (12) |
建立木材干燥过程PSO-LSSVM软测量模型的具体执行步骤如下:
1)选取木材干燥过程的数据作为训练样本;设定延迟时间,用q组数据重构相空间。
2)PSO的参数设置。设置粒子数、搜索范围、终止代数、最大速度Vmax、惯性权值ω、加速因子c1和c2等。
3)初始化所有粒子,在允许范围内随机设置粒子的初始位置和速度,每个粒子的局部最优解pbest设为其初始位置,pbest中的最好值设为gbest。
4)对木材干燥模型进行训练和预测,计算每个粒子的适应值,通过适应度函数求取每个粒子的目标函数。
5)更新每个粒子所经过的最优位置pbest;更新群体所经历过的最优位置gbest。
6)更新当前粒子的速度和位置。
7)检查是否符合结束条件,满足下面任何一个条件都结束操作,终止迭代;否则返回第4)步,继续执行操作。
条件1:达到最大迭代次数;
条件2:取得足够好的适应值;
条件3:最优解不再改变。
8)利用PSO寻优得到的LS-SVM最优惩罚因子c和核函数参数γ,训练样本数据得到木材干燥过程的PSO-LSSVM软测量模型,预测木材含水率并输出最终结果。
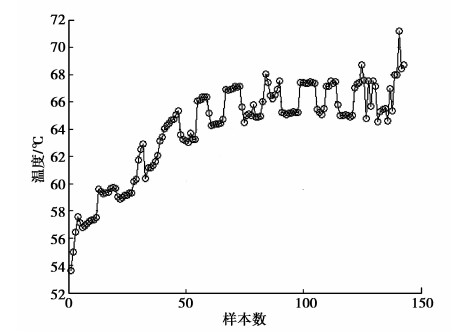
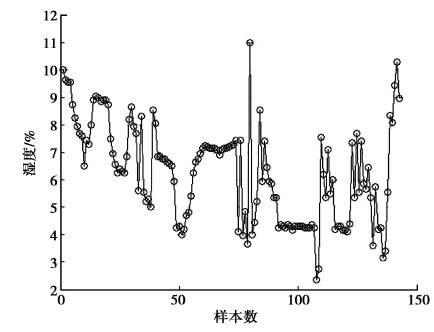
2.2 仿真实验及结果实验选取水曲柳作为试材,利用PSO优化的LS-SVM软测量建模方法对水曲柳干燥过程的木材含水率进行建模和仿真。通过均方根误差(RMSE)描述软测量模型的准确性。在水曲柳软测量建模实验中,木材的初始含水率为71%,终含水率为8%。木材干燥过程可以分为预热、等速干燥、减速干燥3个阶段。减速干燥阶段的模型相对复杂,因此,主要建立水曲柳减速干燥阶段的软测量模型。选取水曲柳实际干燥过程中减速干燥阶段采集的143组数据作为实验样本数据。143组数据的组成结构相同,每组数据都是在同一木材干燥窑内同一时间测得的,包括干燥过程的窑内温度、湿度以及对应的木材含水率数值。在143组样本中,温度的变化范围是53.6~71.2 ℃,湿度的变化范围是2.35%~11%,木材含水率的变化范围是从8.89%~30%,三者间存在强耦合和强非线性关系。PSO-LSSVM软测量模型的143组温度输入曲线如图 2所示,湿度输入曲线如图 3所示。
|
图2 PSO-LSSVM软测量模型温度输入曲线 Fig. 2 Temperature input curve of PSO-LSSVM soft sensor model |
|
图3 PSO-LSSVM软测量模型湿度输入曲线 Fig. 3 Humidity input curve of PSO-LSSVM soft sensor model |
PSO-LSSVM软测量模型仿真实验共用143组数据。首先,利用第1~3组,共3组数据重构LS-SVM的相空间;然后,通过PSO算法对LS-SVM的惩罚因子c和核函数参数γ进行自动寻优,利用第4~103组,共100组训练数据建立木材含水率软测量模型;最后把第104~143组,共40组数据中的温度和湿度值输入给模型,由模型得出木材含水率的预测值,将得出的预测值与第104~143组数据中的实际值进行比较给出偏差。
在PSO-LSSVM软测量模型建立过程中,PSO算法主要目的是选取惩罚系数c和核函数参数γ的最优值,使得软测量模型的性能达到最优。在建立水曲柳干燥过程模型时,首先设置PSO算法的初始值,选取粒子个数为20,最大循环次数为100,粒子维数为2,加速因子c1=1.6和c2=1.5,c的搜索范围[1,1 000],γ的搜索范围[1,100],惯性权值ω随循环次数增加由0.9线性递减至0.4。
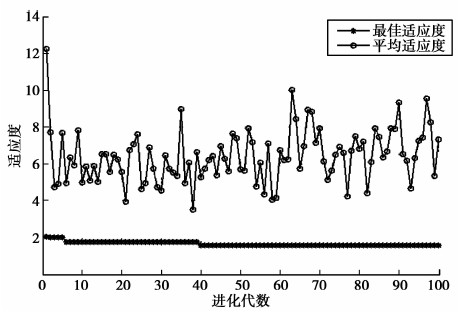
研究共选取样本数据143组,用前3组样本数据重构LS-SVM模型的相空间,训练过程使用中间的100组样本数据,预测过程使用最后的40组样本数据。水曲柳的PSO-LSSVM软测量模型适应度曲线如图 4所示,模型建立过程曲线及预测误差如图 5~图 8所示。图 5和图 6是软测量模型训练过程曲线及误差,图 7和图 8是软测量模型预测过程曲线及误差。图 5~图 8的横坐标均表示样本数。图 6和图 8的纵坐标表示水曲柳干燥过程中木材含水率预测值与实际值的误差大小。
|
图4 PSO-LSSVM软测量模型适应度曲线 Fig. 4 Fitness curves of PSO-LSSVM soft sensor model |
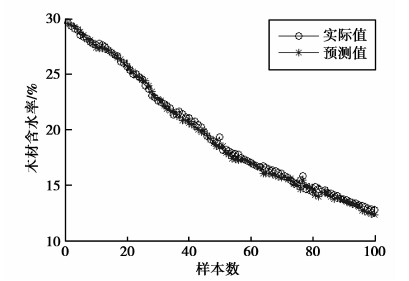
|
图5 PSO-LSSVM软测量模型训练过程曲线 Fig. 5 Training process curves of PSO-LSSVM soft sensor model |
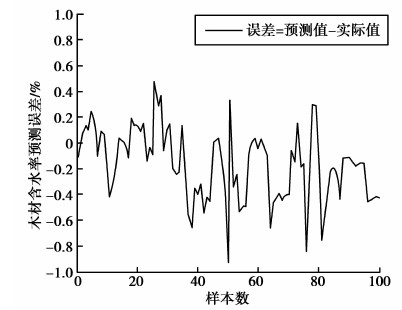
|
图6 PSO-LSSVM软测量模型训练过程的误差曲线 Fig. 6 Training process error curve of PSO-LSSVM soft sensor model |
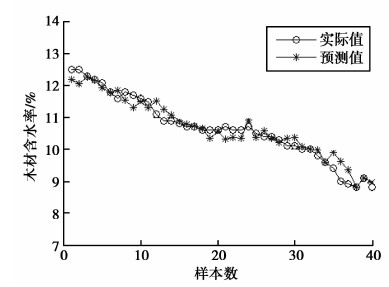
|
图7 PSO-LSSVM软测量模型预测过程曲线 Fig. 7 Prediction process curves of PSO-LSSVM soft sensor model |
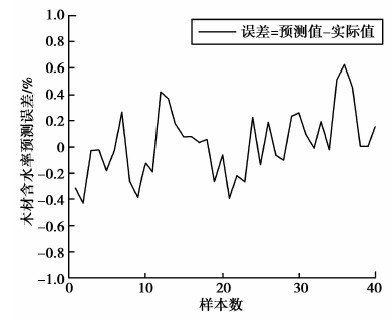
|
图8 PSO-LSSVM软测量模型预测过程的误差曲线 Fig. 8 Prediction process error curve of PSO-LSSVM soft sensor model |
PSO-LSSVM软测量建模实验运行时间为78.63 s,其中,一次训练时间为1.93 s,一次预测时间为0.07 s。模型的不敏感系数ε=0.2,经过寻优后得到的惩罚因子c为609.5,核函数参数γ为91.25,预测的均方根误差RMSE=0.305 9。
从仿真结果中可以看出,PSO-LSSVM模型对木材干燥过程含水率的软测量精度高,模型训练和预测过程的误差均在±1内。仿真结果表明,PSO-LSSVM方法可以建立干燥过程的木材含水率软测量模型,均方根误差均小,模型精度更高,能够准确预测干燥过程的木材含水率数值。水曲柳的PSO-LSSVM软测量模型参数如表 1所示。
| 表1 PSO-LSSVM软测量模型参数表 Table 1 Parameters of PSO-LSSVM soft sensor model |
在不采用PSO优化算法的情况下,单独的LS-SVM方法通常是进行几十次实验,每次实验指定不同的惩罚因子c和核函数参数γ值,建立模型并比较模型的预测结果,选择最好的一组c和γ值。这种方法不仅浪费时间,而且最终选取的最优参数通常为局部最优值,而不是全局最优值。由仿真结果可见,利用PSO-LSSVM方法可以自动寻找木材干燥过程软测量模型的最优惩罚因子c和核函数参数γ,并且得到的参数值是全局最优值,具有很好的软测量精度,有效避免了反复多次的参数寻优实验,优于单独的LS-SVM方法。
3 结 论针对木材干燥过程具有强耦合、大滞后、非线性的特点以及木材含水率检测存在的问题,提出一种木材含水率软测量方法。研究将PSO-LSSVM方法运用到木材含水率软测量建模上,通过实际测量的木材干燥窑内温度、湿度以及对应的木材含水率值,建立木材含水率软测量模型。利用PSO算法寻找LS-SVM模型的最优惩罚因子c和核函数参数γ,使得软测量模型的准确度更高。通过仿真实验结果可知,建立的PSO-LSSVM软测量模型可以准确预测出木材含水率数据,模型结构简单,泛化能力强,预测精度高,符合实际木材干燥过程的工艺要求。基于PSO-LSSVM方法的软测量模型不需要添加额外设备,在木材干燥上具有一定的可行性和有效性,对木材干燥过程含水率测量具有研究意义。
| [1] | 范宇,张冬妍,孙丽萍.基于LSSVM的木材干燥建模研究[J].自动化仪表,2008,29(12):11-13. FAN Yu,ZHANG Dongyan,SUN Liping.Modeling based on least square support vector machine for wood drying process[J].Process Automation Instrumentation,2008,29(12):11-13.(in Chinese)( 1) 1) |
| [2] | 周永东.木材含水率测量方法及影响因素分析[J].木材工业,2000,14(5):29-30. ZHOU Yongdong.The measurement of wood moisture content and analysis of its influence factors[J].China Wood Industry,2000,14(5):29-30.(in Chinese)( 1) 1) |
| [3] | 何正斌,赵紫剑,伊松林.木材干燥热质传递理论与数值分析[M].北京:中国林业出版社,2013:1-60. HE Zhengbin,ZHAO Zijian,YI Songlin,Wood drying heat mass transfer theory and numerical analysis[M].Beijing:China Forestry Publishing Press,2013:1-60. (in Chinese)( 1) 1) |
| [4] | 菜家斌,董会军.进口木材特性与干燥技术[M].安徽:合肥工业大学出版社,2011:80-120. CAI Jiabin,DONG Huijun.Import wood characteristics and drying technology[M].Anhui:Hefei University of Technology Press,2011:80-120.(in Chinese)( 1) 1) |
| [5] | Hu C P,Hong X B,Liu G X,et al.On-line test system of liquefied ethanol concentration based on soft-sensing technique[J].Science Technology and Engineering,2008,23(5):1183-1187.( 1) 1) |
| [6] | 郭俊,桂卫华.基于网格聚类LS-SVM的铝电解生产过程极距软测量[J].控制与决策,2012,27(8):1261-1264. GUO Jun,GUI Weihua.Soft-sensing of polar distance for aluminum electrolysis production process based on grid-based clustering LS-SVM[J].Control and Decision,2012,27(8):1261-1264.(in Chinese)( 1) 1) |
| [7] | Huang J,Bo Y C,Wang H Y.Electromechanical equipment state forecasting based on genetic algorithm-support vector regression[J].Expert Systems with Applications,2011,38(7):8399-8402.( 1) 1) |
| [8] | Li X F,Zhu W X,Kong L D,et al.Method of multi-feature fusion based on SVM and D-S evidence theory in weed recognition[J].Transactions of the Chinese Society for Agricultural Machinery,2011,42(11):164-168.( 1) 1) |
| [9] | Sancho Salcedo-sanz,Emilio G,Ortiz-garcia.Short term wind speed prediction based on evolutionary support vector regression algorithms[J].Expert Systems with Applications,2011,38(4):4052-4057.( 1) 1) |
| [10] | Cheng J D,Da W S.Multi-classification of pizza using computer vision and support vector machine[J].Journal of Food Engineering,2008,86(2):234-242.( 1) 1) |
| [11] | Liu G H,Zhou D W,Xu H X,et al.Model optimization of SVM for a fermentation soft sensor[J].Expert Systems with Applications,2010,37(4):2708-2713.( 1) 1) |
| [12] | Tang W,Zhang L,Chen T.Sensor dynamic modeling based on genetic optimization LS-SVM algorithm[J].Process Automation Instrumentation,2011,32(3):21-23.( 1) 1) |
| [13] | 叶碎高,彭勇,周惠成.基于PSO参数辨识SVM的中长期径流预测研究[J].大连理工大学学报,2011,51(1):115-120. YE Suigao,PENG Yong,ZHOU Huicheng.Research on support vector machine parameter identification method for middle and long term runoff forecast based on particle swarm optimization algorithm[J].Journal of Dalian University of Technology,2011,51(1):115-120.(in Chinese)( 1) 1) |
| [14] | 苏昭斌,朱人杰,陈红卫.基于粒子群支持向量机的海杂波序列回归预测[J].计算机测量与控制,2014,22(5):1540-1542,1571. SU Zhaobin,ZHU Renjie,CHEN Hongwei.Sea clutter sequences regression prediction based on PSO-SVM method[J].Computer Measurement & Control,2014,22(5):1540-1542,1571.(in Chinese)( 1) 1) |
| [15] | 邵剑生,薛惠锋.冲击地压危险等级预测的PSO-SVM模型[J].西安工业大学学报,2012,32(1):39-42. SHAO Jiansheng,XUE Huifeng.Prediction of rock burst intensity based on PSO-SVM model[J].Journal of Xi'an Technology University,2012,32(1):39-42.(in Chinese)( 1) 1) |
| [16] | Sudheer C,Maheswaran R,Panigrahi B K,et al.A hybrid SVM-PSO model for forecasting monthly stream-flow[J].Neural Computing and Applications,2014,24(6):1381-1389.( 1) 1) |
 2016, Vol. 39
2016, Vol. 39

