行人与车的碰撞安全性已成为目前汽车企业在新车型开发阶段面临的技术挑战。行人腿部保护性能取决于汽车前端的几何造型和汽车前端的接触刚度^[1]，而车辆前端的几何造型在车辆开发的早期阶段就已基本确定，因此提高行人的安全性能需要对汽车前端结构的刚度进行合理设计来控制冲击动能^[2]。在汽车前端模型的行人保护优化设计中，先建立汽车前端结构的参数化模型，以行人下肢模块的损伤指标为目标函数，优化得到各碰撞区域的刚度曲线，然后再利用优化得到的理想刚度曲线指导吸能结构的工程设计。文献[3]对汽车前端结构的多刚体模型进行了优化设计，并分析了汽车前端几何和刚度参数对行人腿部伤害指标的影响趋势。文献[4]基于行人下肢保护性能对汽车前端结构进行了优化，并利用优化的刚度曲线指导吸能结构工程设计。EPP泡沫由于质量轻，吸能效率高而作为传统的吸能结构广泛应用于行人保护设计中^[5]。Sun等^[6]采用塑料栅格吸能结构代替泡沫材料，获得了较理想的刚度特性，并大大提升了吸能效率。文献[7]采用金属薄壁结构作为吸能结构也能满足行人下肢保护要求。以上研究虽然分析了吸能结构对保险杠区域刚度的影响，并根据工程经验对吸能结构提出了设计改进对策，但并未提出一种优化方法来对吸能结构进行优化设计从而满足行人下肢保护性能对保险杠区域的刚度要求。

结构优化方法在汽车碰撞仿真中得到了广泛应用，该方法可以有效提高结构设计效率，在面向碰撞冲击这一类动态问题时多采用近似模型法，如文献[8]为满足轻量化和吸能性能的要求采用Hyperstudy和LS-DYNA联合仿真方法对铝合金防撞梁的截面参数进行优化设计。朱敏等^[9]为减轻B柱质量和提高侧面抗撞性，采用响应面方法对B柱加强板沿高度变化的材料屈服强度进行了优化。目前的结构优化问题大多以某一性能指标为优化目标，如比吸能等。笔者针对行人保护对缓冲块的刚度要求，以保险杠理想刚度曲线为优化目标，运用结构优化方法对缓冲块进行优化设计。以缓冲块的材料刚度和截面形状作为设计变量，以有限元仿真得到的刚度曲线和理想刚度曲线所夹的面积最小为目标，采用自适应响应面方法，利用Hyperstudy和LS-DYNA软件进行优化求解，最终获得符合行人保护要求的刚度曲线。

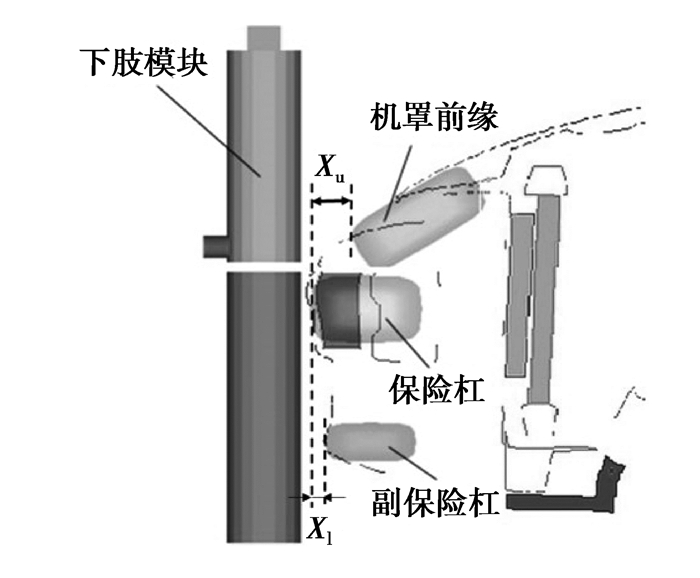
腿部碰撞区域的接触刚度是影响行人下肢保护性能的关键因素，汽车前端结构碰撞区域主要分为机罩前缘、保险杠和副保险杠区域^{[10, 11]}，如图 1所示。研究表明机罩前缘、保险杠和副保险杠的刚度要协调设计才能更好满足行人下肢保护要求^[12]。面向行人下肢保护性能，可利用刚度设计方法得到前端区域的理想刚度曲线，即把对汽车的行人下肢保护性能的要求转化为对汽车前端结构区域的刚度要求。

图1(Fig. 1)

图1 汽车前端结构的简化模型 Fig. 1 Simplified model of the vehicle front-end structure

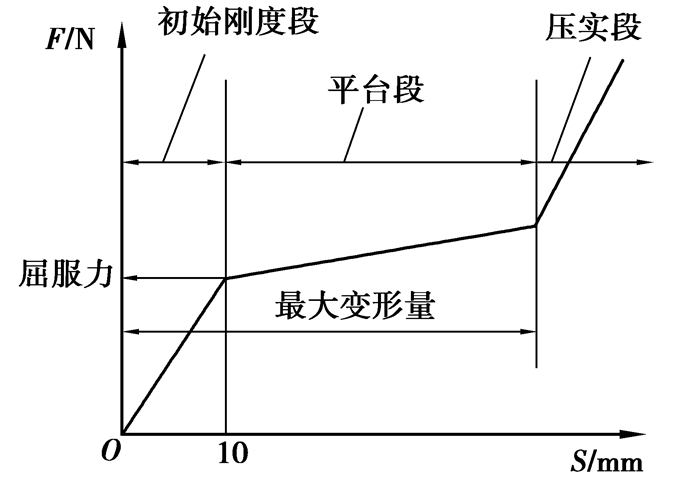
工程上，可以将刚度曲线简化成折线的形式，如图 2所示，可分为初始刚度段、平台段、压实段^[13]。根据车前端结构的几何位置及刚度分布要求^{[14, 15]}，屈服力的变化范围为1 500~2 500 N，最大变形量变化范围为65~80 mm。基于行人保护对车前端多刚体模型进行优化设计^[16]，可以得到保险杠区域的理想刚度曲线。

图2(Fig. 2)

图2 刚度曲线的简化形式 Fig. 2 The Simplified stiffness curve

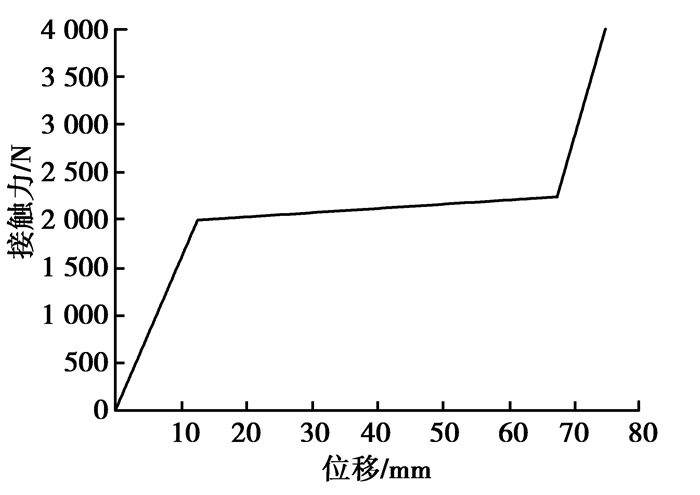
为提升某车型的下肢保护性能，得到其保险杠区域的理想刚度曲线如图 3所示，屈服力为2 000 N，最大变形量为67.5 mm。

图3(Fig. 3)

图3 保险杠区域理想刚度曲线 Fig. 3 The expected stiffness of bumper area

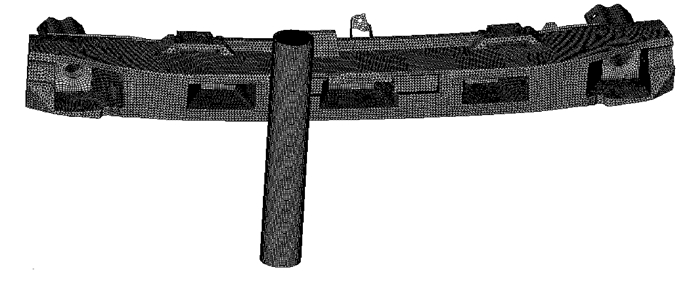
该车原始状态的保险杠刚度曲线可以通过有限元仿真和实验获得。运用Hypermesh对保险杠区域进行有限元网格的划分。该保险杠有限元模型主要包括：泡沫缓冲块、防撞横梁、左右吸能盒，如图 4所示。缓冲吸能材料采用四面体网格划分，外面覆盖一层空材料的壳体单元，用57号材料模拟缓冲块。保险杠防撞横梁、吸能盒采用BT壳单元划分，网格平均大小5 mm，用24号材料模拟。冲击器使用直径为70 mm，质量为13.4 kg的刚性圆柱体，用20号材料模拟，在LS-DYNA中计算求解。

图4(Fig. 4)

图4 保险杠和刚性柱碰撞有限元模型 Fig. 4 The Finite element model of bumper and impactor

根据试验要求，实验室内温度为20±4 ℃，将缓冲块、保险杠横梁、吸能盒固定在支架上，通过推进装置采用水平弹射的推进方式使刚性圆柱体在40 km/h的初速度下撞击缓冲块来模拟行人下肢碰撞。假设刚性圆柱体的中心坐标在P点，当P点与缓冲块中心位置的横向距离不大于420 mm时，进行冲击试验，然后测试绘出保险杠区域的刚度曲线，即缓冲块的接触力和侵入位移曲线。选择距离缓冲块中心位置167 cm处进行行人腿型冲击试验。图 5为试验后缓冲块在冲击位置处的变形图。

图5(Fig. 5)

图5 试验后缓冲块的变形图 Fig. 5 The deformation of bumper after test

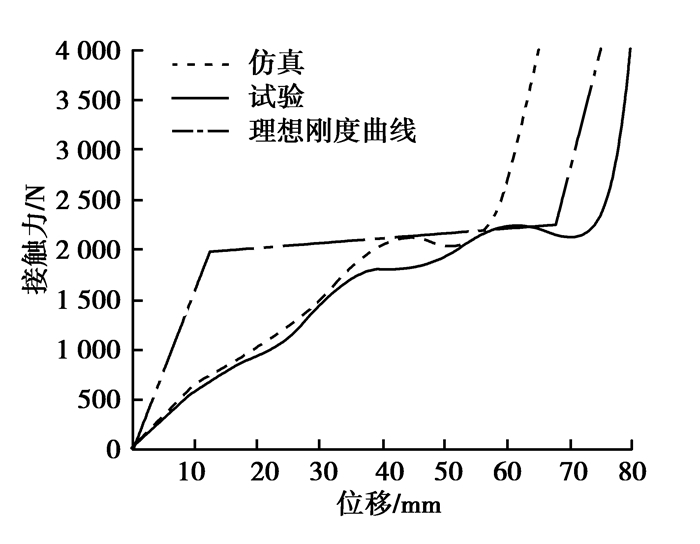
图 6为实验和仿真分析得到的保险杠区域刚度曲线与理想刚度曲线对比图，可以看出：仿真和实验刚度曲线趋势一致，在前52 mm曲线吻合较好，在大变形区域，缓冲块已发生断裂，而仿真中并未模拟出缓冲块的断裂情形，因此实验得到的刚度曲线在大变形区域相对于仿真曲线滞后上升，说明该有限元模型是可靠的。由图 6可知，保险杠区域原始状态的刚度曲线与理想刚度曲线相差较大，曲线没有明显的刚度保持阶段，呈近似直线上升，且前半段刚度太低，不符合行人保护的要求。

图6(Fig. 6)

图6 保险杠刚度曲线对比 Fig. 6 The comparision of bumper stiffness

从分析可知，在刚度测试时变形主要在泡沫区域，而防撞横梁和吸能盒的影响较小，因此需要对缓冲块进行优化设计，以满足刚度要求。

优化对象为泡沫缓冲块，其设计变量包括两个几何形状变量S_h1，S_h2和一个材料刚度变量S_e，设计变量的初始值和取值范围见表 1。

表1(Table 1)

表1 设计变量信息Table 1 design paramters 连续变量 初始值 下限值 上限值 Se 1 1 4 Sh1/mm 8 0 16 Sh2/mm 45 20 70

表1 设计变量信息 Table 1 design paramters

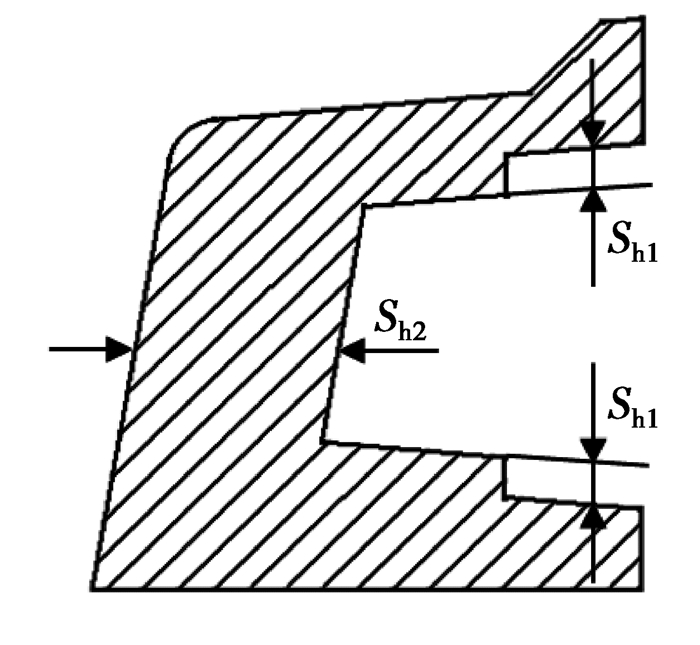
图 7为缓冲块在冲击位置处的截面图，考虑到安装空间的限制，缓冲块的外部轮廓保持不变，对其内部结构进行优化。设计变量S_h1和S_h2控制着缓冲块的结构几何形状。变量S_h1的大小直接影响缓冲块与保险杠横梁的接触面积，变量S_h2决定了缓冲块沿撞击方向的厚度。

图7(Fig. 7)

图7 缓冲块在冲击处的截面形状 Fig. 7 The cross section of damper

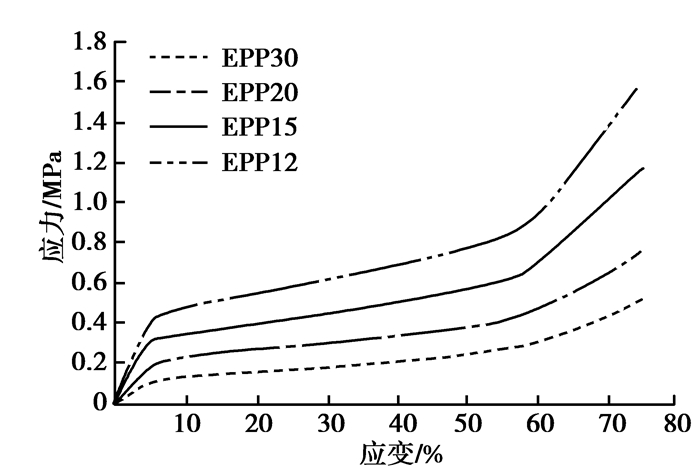
缓冲块最初采用的是30倍发泡率的EPP泡沫材料，由于EPP泡沫的材料刚度偏低，使得保险杠刚度曲线一直都低于理想刚度曲线，需要增加EPP泡沫的材料刚度。不同发泡率下泡沫缓冲块的应力应变曲线如图 8所示。30倍发泡率泡沫材料的应力应变曲线与各曲线之间的相关系数如表 2所示，相关系数均大于0.98，具有高度的线性正相关关系，因此将泡沫缓冲块的材料刚度作为设计变量，其刚度调节通过调整应力应变曲线的放缩系数S_e实现，即对30倍发泡率泡沫的应力应变曲线的应力值进行整体放缩。

图8(Fig. 8)

图8 不同发泡率下泡沫材料的应力应变曲线 Fig. 8 The stress-strain curve under different foaming rate

表2(Table 2)

表2 30倍发泡率泡沫与其他泡沫相关系数Table 2 The correlationi coefficients between 30 times expansion ratio foam and other foams 不同发泡率泡沫 EPP20 EPP15 EPP12 相关系数 0.997 987 0.997 600 0.997 945

表2 30倍发泡率泡沫与其他泡沫相关系数 Table 2 The correlationi coefficients between 30 times expansion ratio foam and other foams

保险杠区域的刚度曲线与理想刚度曲线越接近就越符合行人保护要求，定义优化目标为两曲线所夹的面积最小。该目标函数在软件中的表达如下：

其中：v_1为理想刚度曲线横轴数据；v_2为理想刚度曲线纵轴数据；v_3为仿真曲线横轴数据；v_4为仿真曲线纵轴数据；x是指以两条曲线中横轴最大值较小的那条曲线为横坐标；y是指以两条曲线对应横坐标下的各个点的纵坐标之差为纵坐标；area _value即为点集(x,y)所形成的曲线与水平轴围成的面积。

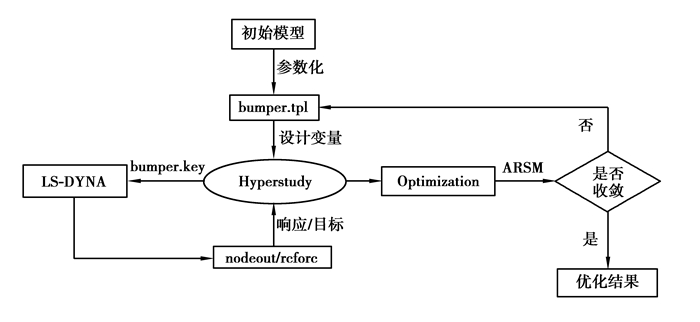
运用Hyperstudy和LS-DYNA软件进行集成优化，在Hyperstudy中调用LS-DYNA求解器，定义设计变量，进行初始分析计算，在结果文件nodeout和rcforc中获取位移和接触力，然后在Optimization模块下定义目标函数。由于自适应响应面法(ARSM)迭代收敛快，拟合精度高，适用于求解非线性问题，所以选择该优化算法求解。将响应和变量的阈值设定为各自初始值的1%，最大迭代次数设定为100次，如果在连续的两次迭代中，所得最优点的响应或者变量的变化小于预设的阈值，则计算结果收敛。优化流程如图 9所示。

图9(Fig. 9)

图9 优化流程图 Fig. 9 The opitmization flow chart

经过42次迭代后收敛，迭代过程中各设计变量和响应量的变化历程如表 3所示。

表3(Table 3)

表3 迭代数据统计结果Table 3 The iterative data 迭代次数 Se Sh1/mm Sh2/mm A/mm2 1 1.00 8.0 45.0 48 362 2 1.15 6.8 45.0 45 653 3 1.15 6.8 42.4 40 982 4 1.10 9.7 47.2 42 617 5 1.23 7.2 46.1 40 648 6 1.31 10.0 49.2 38 893 7 1.44 8.5 44.6 36 720 8 1.57 7.6 42.2 32 591 9 1.72 6.9 40.7 30 563 10 1.83 6.1 39.6 28 366      40 3.69 2.4 16.8 11 758 41 3.58 1.6 20.3 11 144 42 3.50 0.0 18.5 11 094

表3 迭代数据统计结果 Table 3 The iterative data

将初始结果(第1步)和最优结果(第42步)进行对比分析，如图 10所示，可知经过优化后所得的刚度曲线相对于优化前得到了明显的改善，曲线在前半段对比理想刚度曲线有小幅度的偏离，在后半段曲线吻合较好，整体趋势相符。

图10(Fig. 10)

图10 优化前后刚度曲线对比 Fig. 10 The comparision of stiffness curve

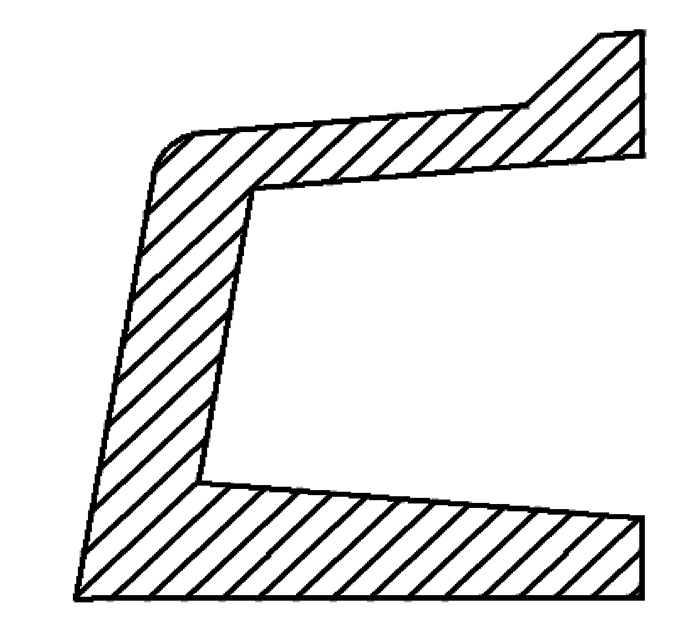
经优化后的泡沫缓冲块的形状变量S_h1为0 mm，S_h2为18.5 mm，其截面形状如图 11所示。

图11(Fig. 11)

图11 优化后缓冲块的截面形状 Fig. 11 The optimized cross section of bumper

优化后泡沫材料的应力应变曲线放缩系数为3.5，该曲线与12倍发泡率的应力应变曲线相近，如图 12所示。

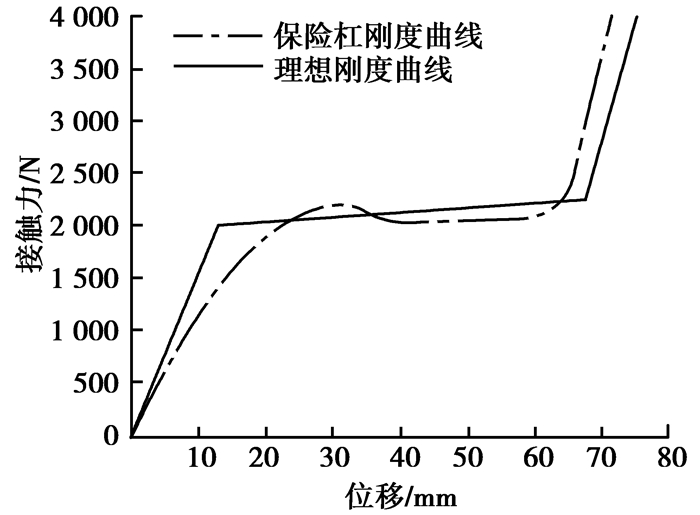
缓冲块采用12倍发泡率的泡沫材料和图 11所示的截面形状，进行有限元仿真分析，得到保险杠区域的刚度曲线，如图 13所示。经对比分析可知，保险杠刚度曲线与理想刚度曲线趋势一致，吻合较好，能够满足行人保护性能对保险杠刚度的要求。

图12(Fig. 12)

图12 优化后缓冲块应力应变曲线 Fig. 12 The optimized stree-strain curve of bumper

图13(Fig. 13)

图13 保险杠刚度曲线 Fig. 13 The stiffness curve of bumper

通过刚度设计可以把汽车的行人保护性能分解成汽车前端各区域的刚度指标，也给结构设计带来了挑战。以保险杠区域的理想刚度曲线为参考目标，采用结构优化方法对缓冲块进行优化设计。以泡沫缓冲块的几何形状和材料刚度为设计变量，将两条刚度曲线之间所夹的面积最小作为优化目标，最终通过自适应响应面法求解得到优化结果，使得结构设计能满足面向行人保护的刚度要求，该优化方法对汽车前端结构的刚度设计以及行人保护具有指导意义。