2. 国家电网公司 西南分部, 成都 610000;
3. 重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044
2. State Grid Corporatron of China Southwest Branch, Chengdu 610000, P. R. China;
3. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, P. R. China
智能变电站作为智能电网建设的重要组成部分,其二次设备的稳定运行对于一次系统的安全性和稳定性至关重要。基于新型智能电子设备和网络化二次系统的智能变电站,其元件组成和系统结构较传统变电站具有较大差别,传统的定期检修方式已不能满足智能变电站安全、稳定经济运行的要求。为提高智能二次设备管理运行的可靠性和经济性,降低变电站全寿命周期成本,亟需开展全面、科学的二次设备状态评估方法研究。
目前,针对二次设备状态评估的研究主要集中在可靠性评价和概率评估。文献[1, 2, 3]应用马尔科夫、故障树及神经网络等方法对继电保护系统进行了可靠性评价,文献[4, 5]建立了继电保护概率故障模型及其失效概率的计算方法。上述研究均从单方面对智能二次设备进行了评价,缺乏对智能二次设备整体运行情况的评估,无法为运行检修人员判断二次设备具体运行状态提供定量的参考依据。
因此,有专家学者提出利用模糊数学对智能变电站进行状态评估。文献[6]利用模糊评判法对智能变电站二次系统进行状态评估,但没有建立能反映各二次设备状态的指标,缺乏工程实际应用价值。文献[7]提出用层次分析法评估智能站通信系统状态,建立了反映通信网络状态的指标体系,但没有建立指标对应状态的隶属度函数,降低了状态评估的准确度。文献[8, 9]基于模糊正态分布隶属度函数与专家评分提出了继电保护系统状态评价的方法,但该方法仅有对保护系统的状态评价,不能完全反映二次系统的整体状态,且各状态指标对保护系统状态影响的权重也缺乏科学严谨的评估。因此,亟需针对复杂且信息获取不完整的智能变电站二次系统探索一种全面定量的状态评估方法。
近年来,灰色聚类和层次分析法成熟应用于“少样本,贫信息”复杂系统的状态评价[10, 11]。同时,智能变电站一体化信息平台[12, 13]和状态监测技术[14, 15]也为其二次设备状态评估奠定了良好的技术基础。为此,文中建立了智能变电站二次设备状态评估指标体系,通过灰色聚类建立灰色状态评估模型,并利用层次分析法得到了状态指标权重,在兼顾复杂性和模糊性的基础上提出了基于灰色层次聚类的智能变电站二次设备状态评估方法。
1 建立状态评估指标体系目前,智能变电站已形成了“三层两网”的结构模型,三层即过程层、间隔层和站控层,两网即过程层网络和站控层网络。过程层包括一次智能设备、合并单元和智能终端,完成变电站电能分配、变换、传输等功能;间隔层包括测控、保护、计量和故障录波装置,实现对一次设备监测、保护与控制功能;站控层包括站级监视控制系统、站域控制、通信系统以及对时系统等,负责面向全站设备的监视、控制、告警及信息交互功能;通信网络,基于IEC61850和以太网技术的智能变电站通信网络是实现全站信息交流共享的通道。
智能变电站二次设备主要功能是反映一次系统电器元件不正常运行状态,并自动、快速、有选择性地将故障元件切除,使元件损坏程度降到最低,保证系统非故障部分正常运行。因此,作为监测控制其他二次设备的站控层装置本身并没有反映和隔离故障功能,其对二次系统运行状态不起决定作用,在此不将其纳入二次设备状态评估范畴。同理,故障录波装置和计量装置也不直接参与监测和控制一次系统运行状态,在此也不将其作为状态评估对象。
作为确保一次系统安全可靠运行的智能变电站二次系统,考虑完成特定功能的某些二次设备测试项目和评估信息具有不可分割的相同来源,将电子式互感器和合并单元作为测量回路整体评估,将交换机和以太网作为通信网络整体评估。另外,运行管理人员还比较注重智能终端、保护装置、测控装置和同步系统等设备的具体运行状态,因此,将其单独进行状态评估,以便能清晰地检测上述装置的实际工作状态。
为了尽量使评估指标全面客观的反映智能变电站二次设备工作状态,选择影响各二次设备运行的主要因素作为其状态指标,且以指标信息易于获取或计算为原则。根据已有研究文献[7, 8, 9]和相关规程规范[16, 17, 18, 19]及测试技术建立智能变电站二次设备状态评估指标体系,如图 1所示。
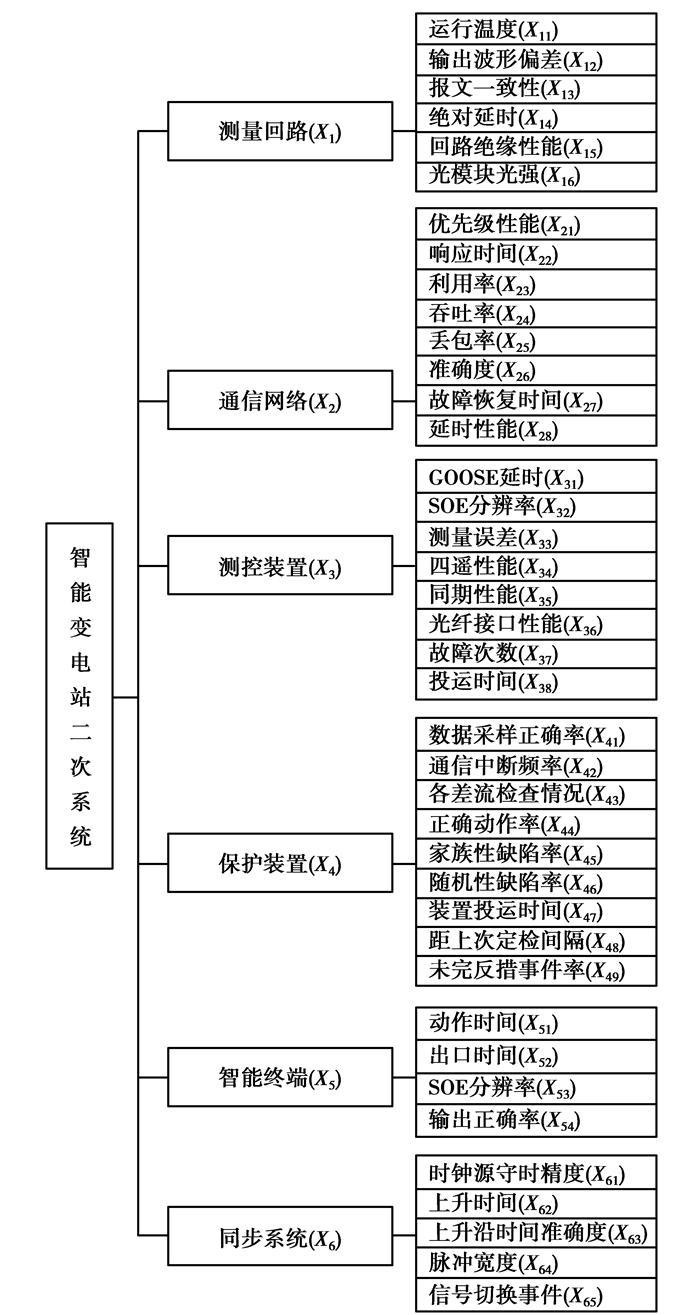
|
图1 状态评估指标体系 Fig. 1 Condition evaluation indices system |
根据故障诊断、维修经验和专家分析,建议将智能变电站二次设备状态分为:良好、一般、注意、严重4种情况,即评语集为:V={严重、注意、一般、良好}={v1、v2、v3、v4}。各二次设备整体状态得分越高,说明其状态越好,状态具体划分及其对应维修决策如表 1。
| 表1 二次设备状态定义 Table 1 Definition of secondary equipment conditions |
在智能变电站二次设备状态评估中,为了提高状态评估的全面性和真实性,防止单一专家对指标判断的主观性,聘请s个专家根据其获取的状态信息和运行经验对m个评估指标进行评分,以此来评估智能变电站二次设备的总体运行状态。那么,第k(k=1,2,3,…,s)个专家对于第h个评估指标给出的评分为ghk,根据所有专家评分结果可得状态指标评估样本矩阵
| $G = \left[ {\begin{array}{*{20}{c}} {g_1^1}&{g_1^2}& \ldots &{g_1^s}\\ {g_2^1}&{g_2^2}& \ldots &{g_2^s}\\ \vdots & \vdots &{}& \vdots \\ {g_m^1}&{g_m^2}& \cdots &{g_m^s} \end{array}} \right] = \left( {g_h^k} \right)m{\rm{ \times }}s.$ | (1) |
建立智能变电站二次设备灰色聚类评估模型主要就是确定状态等级、灰数及其对应的灰色聚类函数。所谓灰色聚类函数,也称白化权函数,其取值介于0~1之间变化,其值越大,灰色系统白化程度越高,系统运行状态越佳。
根据表 1所示的二次设备状态定义,建立如式(2)的灰数和白化权函数。
| $\begin{array}{l} {f_{v1}}\left( {g_h^k} \right) = \left[ {\begin{array}{*{20}{c}} 0& - &2&4 \end{array}} \right],\\ {f_{v2}}\left( {g_h^k} \right) = \left[ {\begin{array}{*{20}{c}} 4&5& - &6 \end{array}} \right],\\ {f_{v3}}\left( {g_h^k} \right) = \left[ {\begin{array}{*{20}{c}} 6&7& - &8 \end{array}} \right],\\ {f_{v4}}\left( {g_h^k} \right) = \left[ {\begin{array}{*{20}{c}} 8&9& - &{10} \end{array}} \right], \end{array}$ | (2) |
式中,fve(ghk)表示二次设备状态评估指标专家评分为ghk时其所对应状态等级vn(n=1,2,3,4)的系数,如图 2所示。
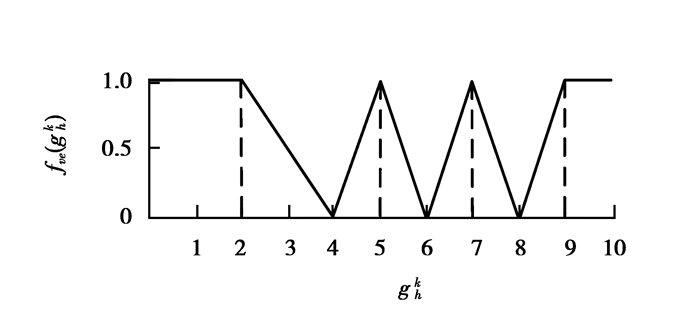
|
图2 健康状态的白化权函数 Fig. 2 The whitenization function of health state |
由此,式(2)改写为
| $\begin{array}{l} {f_{v1}}\left( {g_h^k} \right) = \left\{ \begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \le g_h^k \le 2,\\ \frac{{4 - g_h^k}}{2}\;\;\;\;\;\;\;2 \le g_h^k \le 4,\;\;\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;g_h^k \ge 4,\; \end{array} \right.\\ {f_{v2}}\left( {g_h^k} \right) = \left\{ \begin{array}{l} 0\;\;\;\;\;\;\;\;\;\;\;g_h^k \le 4,\;\\ g_h^k - 4\;\;\;\;\;4 < g_h^k \le 5,\\ 6 - g_h^k\;\;\;\;\;\;5 < g_h^k \le 6,\\ 0\;\;\;\;\;\;\;\;\;\;\;\;g_h^k > 6, \end{array} \right.\\ {f_{v3}}\left( {g_h^k} \right) = \left\{ \begin{array}{l} 0\;\;\;\;\;\;\;\;\;\;\;\;\;g_h^k \le 6,\\ g_h^k - 6\;\;\;\;\;\;6 < g_h^k \le 7,\\ 8 - g_h^k\;\;\;\;\;\;\;7 < g_h^k < 8,\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;g_h^k \ge 8, \end{array} \right.\\ {f_{v4}}\left( {g_h^k} \right) = \left\{ \begin{array}{l} 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;g_h^k \le 8,\\ g_h^k - 8\;\;\;\;\;\;\;\;\;8 < g_h^k < 9,\\ 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;g_h^k \ge 9. \end{array} \right. \end{array}$ | (3) |
对于状态评估指标xij(i=1,2,…,6;j=1,2,…,9),第n(i=1,2,…,4)个评估灰类的灰色评估系数记为yij,n,各个评估灰类的总灰色评估系数记为yij,属于第n个评估灰类的灰色评估权记为rij,n,则
| ${y_{ij,n}} = \sum\limits_{k = 1}^s {{f_{{v_n}}}\left( {g_h^k} \right)} ,$ | (4) |
| ${y_{ij}} = \sum\limits_{n = 1}^e {{y_{ij,n}}} ,$ | (5) |
| ${r_{ij,n}} = \frac{{{y_{ij,n}}}}{{{y_{ij}}}}.$ | (6) |
由于各状态评估指标反映二次设备运行状态的重要程度是不相同的,为了客观评价二次设备状态,需要对各指标的相对重要性(即权重)进行估测。层次分析法已广泛应用于多层次、多变量、结构复杂系统的权重确定,是一种定量与定性分析相结合的有效权重计算方法。步骤如下:
1)建立层次结构体系
分析智能变电站二次系统各设备或指标之间的关系,建立如图 1所示智能变电站二次系统或设备的层次结构。
2)构建判断矩阵
建立层次结构模型后,按照层次分析法中1~9标度原则(表 2),建立各状态指标的判断矩阵A=(apq)N×N,其中apq表示下层元素xp与xq相对上层x的重要性的量化值。
| 表2 层次分析法标度值及含义 Table 2 AHP scale value and meaning |
3)验证状态指标权重的有效性
为验证二次设备状态评估指标权重的有效性,需要对判断矩阵A=(apq)N×N按式(7)进行一致性检验为
| ${C_{\rm{I}}} = \frac{{{\lambda _{\max }} - N}}{{N - 1}},{C_{\rm{R}}} = \frac{{{C_{\rm{I}}}}}{{{R_{\rm{I}}}}},$ | (7) |
式中,λmax和N分别为判断矩阵A的最大特征值和阶数;RI为平均随机一致性指标,其取值见表 3所示。
| 表3 RI 取值 Table 3 RI values |
若CR<0.1时,所建立的判断矩阵A有效,否则需要重新建立判断矩阵,直到CR<0.1。
4)求取指标权重
判断矩阵成立后,采用和法原理求各状态指标权重为
| ${w_p} = \frac{1}{N}\sum\limits_{q = 1}^N {\left( {\frac{{{a_{pq}}}}{{\sum\limits_{k = 1}^N {{a_{kq}}} }}} \right)} .$ | (8) |
根据式(8)计算图 1所示的二次设备xi对智能变电站二次系统权重为wi,二次设备xi的第j个状态指标xij权重为wij。由此,可得状态指标xij对智能变电站二次系统的组合权重为
| ${W_{ij}} = {w_i}{\rm{ \times }}{w_{ij}}.$ | (9) |
设评估对象关于第n灰类的综合聚类系数为
| ${\zeta _n}{\rm{ = }}\sum\limits_{i = 1}^m {\left( {{r_{\rm{n}}}{\rm{ \times }}W} \right)} .$ | (10) |
选取$\zeta _n^*=\mathop {\max }\limits_{1 \le n \le e} \left\{ {{\zeta _n}} \right\}$作为状态评估的最终结果。当评估对象为智能变电站二次设备时,rn、W分别为设备级的评估权和指标权重;当评估对象为智能变电站二次系统时,rn、W分别为对应系统级的评估权和指标权重。
3 仿真算例根据某地区220 kV智能变电站二次系统一体化信息平台和运行管理系统所获得的运行参数,邀请4名专家对智能变电站二次设备状态评估指标进行评分,建立其样本评估矩阵D,如式(11)所示。
| $D = \left[ {\begin{array}{*{20}{c}} 3&{2.5}&3&4\\ 3&{3.5}&2&{3.8}\\ {6.5}&{7.5}&6&7\\ 9&{8.5}&8&{7.8}\\ {8.5}&9&{9.2}&{9.5}\\ 4&{3.5}&{2.6}&3\\ {7.5}&{9.5}&8&9\\ {6.5}&8&{7.5}&7\\ 8&{7.8}&6&{6.5}\\ 7&6&{6.5}&8\\ 9&{7.5}&8&{9.5}\\ {8.5}&8&9&{8.5}\\ {7.8}&{8.6}&8&{7.5}\\ 9&{9.5}&{8.5}&9\\ 8&{8.5}&8&9\\ 7&{6.5}&{7.5}&8\\ 9&{9.5}&9&{9.5}\\ {8.5}&8&{8.5}&8\\ 7&{6.5}&8&{7.5}\\ {9.5}&8&{8.5}&9\\ \vdots & \vdots & \vdots & \vdots \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \vdots & \vdots & \vdots & \vdots \\ {6.5}&7&{8.5}&{7.5}\\ {8.5}&8&9&{8.5}\\ 8&8&{8.5}&{8.5}\\ 9&{9.5}&9&{8.5}\\ 7&{6.5}&{7.5}&8\\ {8.5}&9&{9.5}&{9.5}\\ 8&{8.5}&9&{9.5}\\ 9&{8.5}&{9.5}&{8.5}\\ 7&{6.5}&8&{7.5}\\ {8.5}&8&9&{9.5}\\ 9&{9.5}&9&{8.5}\\ 5&{5.5}&6&5\\ 6&{4.5}&5&{5.5}\\ {6.5}&8&{7.5}&8\\ 8&7&{7.5}&{7.5}\\ 9&{9.5}&{9.5}&9\\ {8.5}&{8.5}&9&{9.5}\\ {9.5}&9&9&{9.5}\\ {9.5}&{8.5}&9&9\\ 8&{8.5}&9&{8.5} \end{array}} \right].$ | (11) |
依据2.3和2.4节,以测量回路报文一致性状态指标x13为例,由式(3)、式(4)求得状态指标x13的4个评估灰类的灰色评估系数分别为:当n=1时,${y_{13.1}}=\sum\limits_{k=1}^4 {{f_{v1}}\left({g_h^k} \right)=f_{v1}^{\left(6 \right)}+f_{v1}^{\left({7.5} \right)}+f_{v1}^{\left(6 \right)}+f_{v1}^{\left(7 \right)}}=0$;当n=2时,y13,2=1.750;当n=3时,y13,3=3.125;当n=4时,y13,4=3.125。进一步由式(5)求得总评估系数${y_{13}}={y_{13,n}}={y_{13,1}}+{y_{13,2}}{y_{13,3}}+{y_{13,4}}=8$。最后由式(6)求得指标x13的4个灰色评估权:r13,1=0,r13,2=0.22,r13,3=0.39,r13,4=0.39。同理,可得其余39个状态指标的灰色评估权r为
| $r = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 1&0&0&0\\ {0.39}&{0.39}&{0.22}&0\\ 0&0&{0.1}&{0.9}\\ 0&0&0&1\\ 1&0&0&0\\ 0&0&{0.17}&{0.83}\\ 0&0&1&0\\ 0&0&1&0\\ 0&0&1&0\\ 0&0&0&1\\ 0&0&0&1\\ 0&0&{0.77}&{0.23}\\ 0&0&0&1\\ 0&0&0&1\\ 0&0&1&0\\ 0&0&0&1\\ 0&0&0&1\\ 0&0&1&0\\ 0&0&0&1\\ \vdots & \vdots & \vdots & \vdots \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \vdots & \vdots & \vdots & \vdots \\ 0&0&{0.72}&{0.28}\\ 0&0&0&1\\ 0&0&0&1\\ 0&0&0&1\\ 0&0&1&0\\ 0&0&0&1\\ 0&0&0&1\\ 0&0&0&1\\ 0&0&1&0\\ 0&0&0&1\\ 0&0&0&1\\ 0&1&0&0\\ 0&1&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&1&0\\ 0&0&0&1\\ 0&0&0&1\\ 0&0&0&1\\ 0&0&0&1 \end{array}} \right].$ | (12) |
根据2.5节,由层次分析法建立智能变电站各二次设备相对二次系统的权重判断矩阵为
| $A = \left[ {\begin{array}{*{20}{c}} 1&{1/2}&{1/2}&{1/4}&{1/3}&{1/6}\\ 2&1&{1/3}&4&{1/6}&7\\ 2&3&1&3&{1/4}&{1/2}\\ 4&{1/4}&{1/3}&1&2&5\\ 3&6&4&{1/2}&1&3\\ 6&{1/7}&2&{1/5}&{1/3}&1 \end{array}} \right].$ | (13) |
上述矩阵满足层次分析法的一致性要求,应用式(8)求得各二次设备的权重wi(i=1,…,6)为
| $w = \left[ {0.208\;\;0.083\;\;0.208\;\;0.292\;\;0.042\;\;0.167} \right].$ | (14) |
同理,可得各状态指标关于与其对应二次设备的权重为
| $\begin{array}{l} {w_{ij}}\left( {j{\rm{ = 1,}} \cdots {\rm{,6}}} \right) = \left[ {{\rm{0}}{\rm{.098}}\;\;{\rm{0}}{\rm{.283}}\;\;{\rm{0}}{\rm{.208}}\;\;{\rm{0}}{\rm{.202}}\;\;{\rm{0}}{\rm{.082}}\;\;{\rm{0}}{\rm{.127}}} \right],\\ {w_{ij}}\left( {j{\rm{ = 1,}} \cdots {\rm{,8}}} \right){\rm{ = }}\left[ {{\rm{0}}{\rm{.128}}\;\;{\rm{0}}{\rm{.083}}\;\;{\rm{0}}{\rm{.110}}\;\;{\rm{0}}{\rm{.192}}\;\;{\rm{0}}{\rm{.042}}\;\;{\rm{0}}{\rm{.1}}\;\;{\rm{0}}{\rm{.26}}\;\;{\rm{0}}{\rm{.08}}} \right],\\ {w_{ij}}\left( {j{\rm{ = 1,}} \cdots {\rm{,9}}} \right){\rm{ = }}\left[ {{\rm{0}}{\rm{.108}}\;\;{\rm{0}}{\rm{.091}}\;\;{\rm{0}}{\rm{.1}}\;\;{\rm{0}}{\rm{.08}}\;\;{\rm{0}}{\rm{.072}}\;\;{\rm{0}}{\rm{.07}}\;\;{\rm{0}}{\rm{.12}}\;\;{\rm{0}}{\rm{.92}}\;\;{\rm{0}}{\rm{.1}}} \right],\\ {w_{ij}}\left( {j{\rm{ = 1,}} \cdots {\rm{,4}}} \right) = \left[ {{\rm{0}}{\rm{.292}}\;\;{\rm{0}}{\rm{.209}}\;\;{\rm{0}}{\rm{.208}}\;\;{\rm{0}}{\rm{.363}}} \right],\\ {w_{ij}}\left( {j{\rm{ = 1,}} \cdots {\rm{,5}}} \right) = \left[ {{\rm{0}}{\rm{.188}}\;\;{\rm{0}}{\rm{.292}}\;\;{\rm{0}}{\rm{.228}}\;\;{\rm{0}}{\rm{.167}}\;\;{\rm{0}}{\rm{.125}}} \right]. \end{array}$ | (15) |
将式(14)、式(15)代入式(9)即可得各指标组合权重wij(i=1,…,6;j=1,…,9)为
| ${w_{ij}} = \left[ {\begin{array}{*{20}{c}} {0.01}\\ {0.06}\\ {0.01}\\ {0.03}\\ {0.04}\\ {0.04}\\ {0.02}\\ {0.03}\\ {0.02}\\ {0.01}\\ \vdots \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \vdots \\ {0.03}\\ {0.02}\\ {0.04}\\ {0.05}\\ {0.03}\\ {0.03}\\ {0.01}\\ {0.03}\\ {0.01}\\ {0.02} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \vdots \\ {0.01}\\ {0.02}\\ {0.01}\\ {0.03}\\ {0.02}\\ {0.04}\\ {0.03}\\ {0.02}\\ {0.03}\\ {0.01} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \vdots \\ {0.05}\\ {0.01}\\ {0.04}\\ {0.03}\\ {0.01}\\ {0.04}\\ {0.01}\\ {0.01}\\ {0.03}\\ {0.01} \end{array}} \right].$ | (16) |
根据2.6节可得各二次设备和二次系统整体的状态评估结果为ζie(i=1,…,6,7,e=1,…,4),如式(17)所示。其中:i=1~6表示二次设备x1~x6的状态评估结果,i=7为二次系统整体的状态评估结果。
| ${\xi _{ie}} = \left[ {\begin{array}{*{20}{c}} {0.18}&{0.18}&{0.21}&{0.43}\\ {0.38}&{0.26}&{0.25}&{0.11}\\ {0.23}&{0.45}&{0.18}&{0.14}\\ {0.51}&{0.17}&{0.19}&{0.13}\\ {0.46}&{0.28}&{0.12}&{0.14}\\ {0.36}&{0.38}&{0.25}&{0.22}\\ {0.26}&{0.42}&{0.21}&{0.11} \end{array}} \right].$ | (17) |
由此,根据式(17)所示的状态评估结果,可知智能变电站二次系统整体状态为“一般”,应根据规程按计划检修。各二次设备中通信网络、继电保护和智能终端为“良好”状态,测控装置和同步系统为“一般”状态,测量回路为“严重”状态。因此,应立即对测量回路进行检修,排除故障以保障二次系统安全可靠运行。
4 结 论智能变电站二次设备工作状态关系着电网能否安全可靠稳定地运行。针对二次设备复杂的故障原因以及模糊的运行状态信息特征,建立了智能变电站二次设备状态评估指标体系,并引入灰色聚类和层次分析法建立了二次设备状态评估模型。文中所提方法不仅可对二次系统整体进行状态评估,而且可得单独二次设备的状态评估结果,使运行维修人员更加清晰二次系统的运行状态,并有针对性地对其进行状态检修。实例分析表明,该方法为智能变电站二次设备及系统的状态评估提供了一种新型适用途径。
| [1] | 熊小伏,蔡伟贤,周家启,等.继电保护隐藏故障造成输电线路连锁跳闸的概率模型[J].电力系统自动化,2008,32(13):6-10. XIONG Xiaofu, CAI Weixian, ZHOU Jiaqi, et al. Probabilistic model for transmission lines' cascading trips caused by hidden failures in relay protection[J]. Automation of Electric Power Systems,2008,32(13):6-10.(in Chinese)( 1) 1) |
| [2] | 张雪松,王超,程晓东.基于马尔可夫状态空间法的超高压电网继电保护系统可靠性分析模型[J].电网技术,2008,32(13):94-99. ZHANG Xuesong, WANG Chao, CHENG Xiaodong. Reliability analysis model for protective relaying system of UHV power network based on markov state-space method[J]. Power System Technology,2008,32(13):94-99.(in Chinese)( 1) 1) |
| [3] | 戴志辉,李芷筠,焦彦军,等.基于BP神经网络的小样本失效数据下继电保护可靠性评估[J].电力自动化设备,2014,34(11):129-134. DAI Zhihui, LI Zhijun, JIAO Yanjun, et al. Reliability assessment based on BP neural network for relay protection system with a few failure data samples[J]. Electric Power Automation Equipment,2014,34(11):129-134.(in Chinese)( 1) 1) |
| [4] | 熊小萍,谭建成,林湘宁.基于动态故障树的变电站通信系统可靠性分析[J].中国电机工程学报,2012,32(34):135-141,20. XIONG Xiaoping, TAN Jiancheng, LIN Xiangning. Reliability analysis of communication systems in substation based on dynamic fault tree[J]. Proceedings of the CSEE,2012,32(34):135-141.(in Chinese)( 1) 1) |
| [5] | 戴志辉,王增平,焦彦军,等.继电保护原理性运行失效概率模型[J].电力系统自动化,2010,34(23):16-20. DAI Zhihui, WANG Zengjun, JIAO Yanjun, et al. An operation failure probability model for power system protection[J]. Automation of Electric Power Systems,2010,34(23):16-20.(in Chinese)( 1) 1) |
| [6] | 潘华君,许晓峰,许东,等.基于模糊评判法的智能变电站二次系统状态评估[J].沈阳工程学院学报(自然科学版),2014,10(2):143-147. PAN Huajun, XU Xiaofeng, XU Dong. Status evaluation of secondary system in intelligent substation based on comprehensive fuzzy evaluation method[J]. Journal of Shenyang Institute of Engineering,2014,10(2):143-147.(in Chinese)( 1) 1) |
| [7] | 戴婷,宋斌,彭正洪.基于灰色层次分析法的变电站通信网络状态评价[J].武汉大学学报(工学版),2011,44(4):526-529. DAI Ting, SONG Bin, PENG Zhenghong. Substation communication network condition evaluation based on grey analytic hierarchy process[J].Engineering Journal of Wuhan University,2011,44(4):526-529.(in Chinese)( 2) 2) |
| [8] | 吴姜,蔡泽祥,胡春潮,等.基于模糊正态分布隶属函数的继电保护装置状态评价[J].电力系统保护与控制,2012,40(5):48-52. WU Jiang, CAI Zexiang, HU Chunchao, et al. Status evaluation of protective relays based on the membership function in fuzzy normal distribution[J]. Power System Protection and Control,2010,40(5):48-52.(in Chinese)( 2) 2) |
| [9] | 王跃强,廖华兴,袁晓青,等.基于保信系统的继电保护状态评价系统的开发与应用[J].电力系统保护与控制,2014,42(8):134-139. WANG Yueqiang, LIAO Huaxing, YUAN Xiaoqing, et al. Development and application of relay protection condition evaluation system based on fault information processing system[J]. Power System Protection and Control,2014,42(8):134-139.( 2) 2) |
| [10] | Tang W H, Spurgeon K, Wu Q H, et al. An evidential reasoning approach to transformer condition assessments[J]. IEEE Transaction on Power Delivery,2004,19(4):1696-1703.( 1) 1) |
| [11] | 丁亚非,李文生,徐跃.灰色层次聚类法在通信对抗装备效能评估中的应用[J].火力与指挥控制,2011,36(1):103-107,113. DING Yafei, LI Wensheng, XU Yue. Application of grey hierarchy cluster algorithm to effectiveness evaluation of communication EW equipment[J]. Fire Control & Command Control,2011,36(1):103-107,113.(in Chinese)( 1) 1) |
| [12] | 王冬青,李刚,何飞跃.智能变电站一体化信息平台的设计[J].电网技术,2010,34(10):20-25. WANG Dongqing, LI Gang, HE Feiyue. Design of integrative information platform for smart substations[J]. Power System Technology,2010,34(10):20-25.(in Chinese)( 1) 1) |
| [13] | 蒋宏图,袁越,杨昕霖.智能变电站一体化信息平台的设计[J].电力自动化设备,2011,31(8):131-134. JIANG Hongtu, YUAN Yue, YANG Xilin. Design of integrative information platform for smart substations[J]. Electric Power Automation Equipment,2011,31(8):131-134.(in Chinese)( 1) 1) |
| [14] | Pylvanainen J K, Nousiainen K, Verhop P. Studies to utilize loading guides and ann for oil-immersed distribution transformer condition monitoring[J]. IEEE Transaction on Power Delivery,2007,22(1):201-207.( 1) 1) |
| [15] | Mcarthur S D J, Strachan S M, Jahn G. The design of a multi-agent transformer condition monitoring system[J]. IEEE Transaction on Power Systems,2004,19(4):1845-1852.( 1) 1) |
| [16] | Q/GDW 383-2009智能变电站技术导则[S].北京:国家电网公司,2009. Q/GDW 383-2009 Smart substation technical guidelines[S]. Beijing:State Grid Company,2009.(in Chinese)( 1) 1) |
| [17] | Q/GDW 429-2010智能变电站网络交换机技术规范[S]. 北京:国家电网公司, 2010. Q/GDW 429-2010 Smart substation network switch technical specifications[S]. Beijing:State Grid Company,2010.(in Chinese)( 1) 1) |
| [18] | 袁宇波,高磊,卜强生,等.智能变电站集成测试技术与应用[M].北京:中国电力出版社,2013. YUAN Yubo, GAO Lei, BU Qiangsheng, et al. Intelligent substation integration testing technology and applica-tion[M]. Beijing:China Electric Power Press,2013.(in Chinese)( 1) 1) |
| [19] | 何建军,徐瑞林,陈涛.智能变电站系统测试技术[M].北京:中国电力出版社, 2012. HE Jianjun, XU Ruilin, CHEN Tao. Intelligent substation system testing technology[M]. Beijing:China Electric Power Press,2012.(in Chinese)( 1) 1) |
 2016, Vol. 39
2016, Vol. 39

