2. 重质油国家重点实验室, 山东 青岛 266580;
3. 大庆油田采气分公司, 黑龙江 大庆 163000
2. State Key Laboratory in Heavy Oil, Qingdao 266580, Shandong, P. R. China;
3. Gas Production Branch of Daqing Oil Field, Daqing 163000, Helongjiang, P. R. China
在储层出砂、油气层保护、近井带污染与解堵中,分析微粒剥离、沉积与运移的状态与程度,对于分析岩土渗透性变化具有重要影响。前人开展了包括微粒运移与流出量受储层内部和外部因素影响的实验模拟、数值模型建立及规律影响分析在内的大量研究[1, 2],多针对于静态流体或稳态多相渗流环境中。相关模型理论分析约涉及3个方面,一是把颗粒在多孔介质内的运移、沉积现象看作是随机现象,然后用随机过程数学方法进行研究;二是直接根据质量守恒的普遍定律建立颗粒运移、沉积数学模型,研究颗粒的浓度、流动压力等对孔隙堵塞的影响情况;三是通过微粒受力分析,研究微粒剥离、分散、沉积过程中的临界条件[3, 4, 5]。
然而,实际生产中经常伴随着压力和生产参数的波动,工业化的人工波动应用也使得研究弹性波作用下多孔介质渗流中微粒运移过程具有一定的必要性,如低频波动采油技术如何实现近井带解堵。目前,关于该方面的研究论文仍较少,如蒋华义等[6]通过实验方法得到了影响颗粒在多孔介质中运移的因素,以及疏松堵塞和致密堵塞两种情况下的处理方法(前者选择最优频率和振幅即可,后者采用较高的频率和振幅及多次振动);李会平等[7]通过室内实验结合现场试验,发现润湿性、不同油藏油井动态特征(如活跃的边水、稠油油藏)、相数对微粒运移类型均有影响。笔者将基于微粒运移的基本过程和机理,结合弹性波对多孔介质渗流的影响,分析弹性波作用下的微粒剥离、捕集受力,重新建立相应的运移模型并进行分析。
1 胶结类型与运移类型开展弹性波对储层微粒运移作用判别准则与规律分析时,作为研究对象的砂岩,可以分为疏松砂岩、完全胶结砂岩,以及介于两者之间的弱胶结砂岩3种情况。对于疏松砂岩,弹性波对储层微粒运移仅仅直接考虑基质或胶结物颗粒运移即可,无颗粒的脱离过程;对于完全胶结砂岩,弹性波对储层微粒运移需先考虑岩石基质和胶结物的破坏(破坏准则确定和岩石力学参数表征上),然后考虑之后小块的脱落、运移、沉积;对于弱胶结砂岩,弹性波对储层微粒运移一方面考虑岩石基质的破坏及后续脱落基质运移、再沉积,另一方面考虑孔喉中疏松充填物(考虑充填物占基质的比例)的运移。
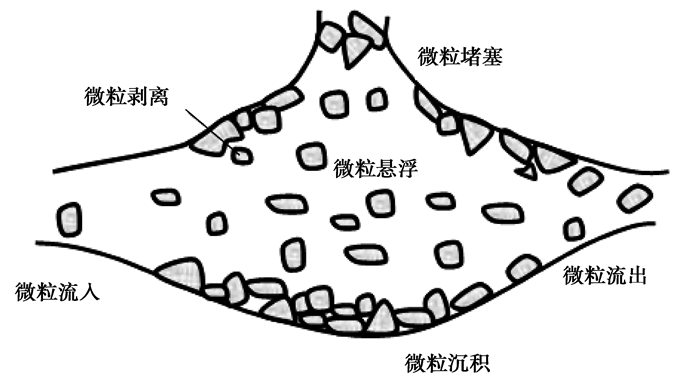
影响颗粒能否“剥离”、“运移”、“流出”的几何约束条件分别为[8]:①地层的孔隙梯度gradΦ在压力梯度gradP分量上的存在;②剥落的砂岩颗粒应小于孔喉尺寸;③微粒通过的孔隙是连通的。对于孔喉内部微粒大小的确定,实验模拟与数值模拟中可直接假设给定颗粒大小,对于天然岩心孔喉内部微粒尺寸可通过铸体薄片、CT扫描等方法进行测量,岩心流出端微粒尺寸可利用可见光、X射线、激光等光学粒度仪进行测量。孔喉中微粒不同运移状态如图 1所示。
|
图1 孔喉中微粒不同运移状态 Fig. 1 Different states of particles in the pore throat |
在微粒运移-分散过程中,微粒受到水动力(提升力、粘附力)、惯性力、重力、静电力(包括范德华力、布朗扩散力、结构力、波恩短程斥力、表面双电层排斥力)等的作用[9, 10],弹性波作用下微粒还受到声波附加的水动力拉力,静电力受微粒粒径、微粒间距离、矿化度、温度的影响。在外来流速不大且较小波动、矿化度较低条件下,表面势能成为主导因素。重力和布朗扩散力对不同粒径的微粒作用大小有所不同:R>2 μm时,重力作用远大于布朗扩散力,大多情况下,如注水中重力沉降作用不能被忽略,除非流固密度差非常小、接近0;R=1~2 μm时,两者大小视具体情况而定;R>2 μm时,对于任何尺寸的微粒,在注水过程中,惯性力可以忽略不计。
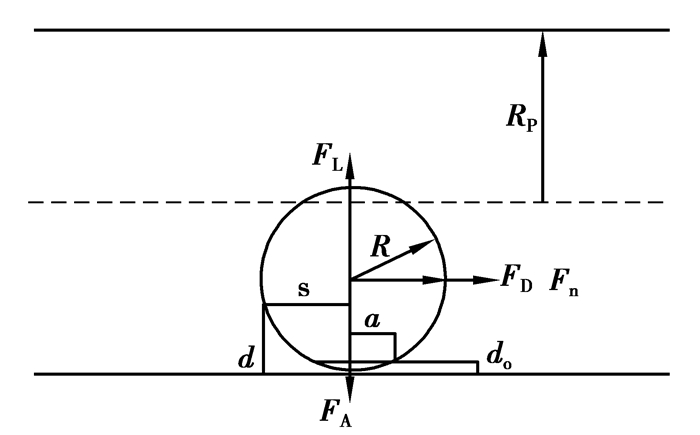
2.1 微粒释放机理岩石孔喉内流体的流动会对壁面的微粒产生拉拽和摩擦等作用,当这些动力的作用大于微粒本身的胶结强度时时,微粒就会从壁面脱落进入流体中,随流体在孔喉内流动。孔喉微粒受力分析如图 2所示。
|
图2 孔喉微粒受力分析图 Fig. 2 Forces on the particlesin the pore throat |
微粒受到声波附加拉力FD、提升力FL的作用下,克服重力Fg、粘滞力Fη、静电力FA,使微粒从孔隙表面脱离。波动水驱条件下,微粒所受水动力影响加剧,微粒间距离增加,水动力成为主导因素,文中只考虑静电力中的结构力。剥离过程中包括了原有基质、胶结物和充填物的剥离,以及再沉积后微粒的剥离,为了研究的方便,当注水流速较大且波动较为剧烈时,忽略再沉积速度。微粒受力达到与孔壁脱落的临界平衡条件时[11],力矩满足
| ${L_x}\left( {{F_{\text{D}}} + {F_\eta }} \right) = {L_y}\left( {{F_{\text{A}}} + {F_g}} \right) - {L_z}{F_{\text{L}}}$ | (1) |
声波作用在微粒上的振荡拉力FD的最大值为
| ${F_{\text{D}}} = 6\pi {\text{R}}{{\text{A}}_d}\eta {v_{\max }}$ | (2) |
悬浮岩石颗粒当接近孔喉壁面时,会受到一个排斥的举升力FL[12, 13],但当微粒被剥离前,由于与壁面为一体,举升力可忽略,
| $ {F_{\text{L}}} = \chi {R^3}\sqrt {\frac{{{\rho _s}\eta v_{\text{w}}^3}}{{8R_{{\text{ch}}}^3}}} $ | (3) |
根据圆形颗粒在Hele-Shaw平板流中的粘滞拖拽力公式[12]为
| ${F_\eta } = \frac{{\zeta \pi \eta {v_w}{R^2}}}{{2{R_{{\text{ch}}}}}}$ | (4) |
重力(当微粒未被剥离时不考虑浮力)为
| ${F_g} = \frac{{4\pi {R^3}{\rho _s}g}}{3}$ | (5) |
结构力参考Barton不规则粗糙面结构模型为
| ${F_{\text{A}}} \approx {\tau _{{\text{cr}}}} = \sigma \tan \left[{JRC\log \left( {\frac{{JRC}}{\sigma }} \right) + \theta } \right]$ | (6) |
对于疏松砂岩,由于岩石颗粒粒径通常都大于100 μm,根据文献可知岩石颗粒的临界剪切力为[8]
| ${F_{\text{A}}} \approx {\tau _{{\text{cr}}}} = \frac{{4\left( {{\rho _{\text{s}}} - {\rho _{\text{f}}}} \right)gR\tan \theta }}{{3\alpha }}$ | (7) |
式中:vmax为声波作用下流体最大速度,与声波频率有关,vmax=[u(r=0,t)max+v],u(r=0,t)为静止流体中声波振荡拉力导致的流速;Ad与微粒半径、孔道半径之比有关;v是液体原始流速;R为球形微粒半径;Rch为孔喉平均半径;χ为举升系数;η为流体粘度;ρs为砂粒的密度;ρf为流体的密度;θ为岩石颗粒的摩擦角;α为地层流体作用于岩石颗粒上的有效摩擦面积与最大截面积πR2之比;φ为孔隙度; ζ为经验系数,一般为10~60;σ为法向力;JRC为结构面粗糙系数。
当微粒被剥离时,$\left| {{F_n}} \right| = \left| {\left( {{F_{\text{D}}} + {F_\eta }} \right) - \frac{{{L_y}}}{{{L_x}}}\left( {{F_{\text{A}}} + {F_g}} \right)} \right|$>0,则弹性波作用下的临界流速为
| ${v_c} = \frac{{{L_y}}}{{{L_x}}}\frac{2}{{\pi R\eta }}\frac{{{\tau _{{\text{cr}}}} + \frac{4}{3}\pi {R^3}{\rho _{\text{s}}}g}}{{12{A_d} + \zeta \xi }}$ | (8) |
当微粒处于剥离后沉积状态,$\left| {{F_n}} \right| = \left| {\left( {{F_{\text{D}}} + {F_\eta }} \right) - \frac{{{L_y}}}{{{L_x}}}{F_g} + \frac{{{L_y}}}{{{L_x}}}{F_{\text{L}}}} \right|$>0,则弹性波作用下的临界流速为
| ${v_c}\dot \in \left( {\frac{{4{L_y}\Delta \rho g\pi }}{{3{L_z}\chi }}{{\left( {\frac{{8R_{{\text{ch}}}^3}}{{{\rho _{\text{s}}}{\eta ^3}}}} \right)}^{0.5}},\frac{{8{L_y}\Delta \rho g{R^2}}}{{3{L_x}\eta \left( {12{A_d} + \zeta \xi } \right)}}} \right)$ | (9) |
式中,ξ=R/Rch为微粒与孔喉半径的比值,ξ < 1,当ξ越小时,说明粘滞力所占比重越来越小,而弹性波导致的振荡附加力影响越大。对于临界剪切力τcr,根据岩石类型如疏松岩石、完全胶结、部分胶结岩石的不同而取不同数值。部分研究文献中将微粒剥离的作用力以临界流速vc的形式表示,即vw≥vc时,微粒从基质上剥离释放,当vw < vc时,微粒不会被剥离。
由微粒被剥离时和剥离后沉积再次释放的临界流速可知,临界流速与流体粘度、微粒与孔喉半径比值成反比,与基质胶结程度、结构力、微粒半径、微粒密度成正比;流固密度差越小,剥离后沉积再次释放的临界流速越小,说明重力对微粒运移的影响越小而可以被忽略。
2.2 微粒捕集机理与微粒释放相反,孔喉壁面脱落进入流体中的微粒也有可能会沉降到孔喉壁面上导致孔喉半径减小,甚至当微粒半径大于或者接近喉道半径时会使喉道产生堵塞,使储层的连通性降低。目前,在微粒捕集的模型中,捕集机理主要包括:沉积、直接堵塞和架桥堵塞3种不同情况。①直接堵塞:对于微粒半径大于或者等于喉道半径的情况,微粒流经该喉道时会直接堵塞该喉道,使孔隙配位数降低,网络连通性变差;目前研究的注入悬浮微粒沉积模型中,注入微粒一般要小于孔喉半径。②沉积:在流体流动过程中,流体中悬浮的微粒会有一部分在孔喉壁面沉积,使孔喉尺寸减小。③架桥堵塞:当微粒半径小于喉道半径时,如果孔隙内流体浓度大于一定浓度值,也有可能通过多个微粒架桥的方式将相连的喉道堵塞,降低网络的连通性。通过以下弹性波作用下储层微粒运移模型分析,说明弹性波对微粒捕集的影响。
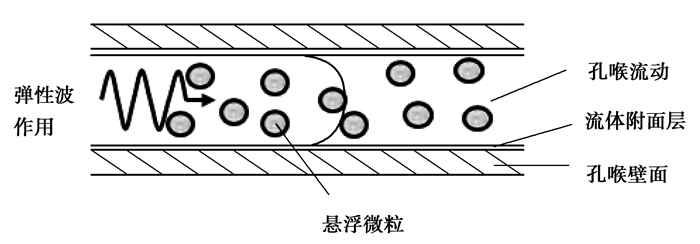
3 弹性波作用下储层微粒运移模型基于弹性波对多孔介质渗流影响的基础作用机理,由于弹性波作用下流固交错移动和射流等,流体流速发生变化[14, 15, 16],微粒运移过程亦发生变化,弹性波对储层微粒运移的作用模型需要同时考虑弹性波作用下多孔介质渗流影响模型和微粒剥离运移捕集模型。弹性波作用下孔喉流体流动如图 3所示。
|
图3 弹性波作用下孔喉流体流动 Fig. 3 Seepage of fluid in the pore throat under elastic wave action |
由于考虑波动对渗流过程影响下的微粒捕集、沉积、运移过程,应采用饱和渗流流体的弹性波传播的流固耦合模型。
饱和渗流流体弹性多孔介质和流体运动方程如下。其中$\left( {\lambda + 2\mu } \right){\nabla ^2}u$为固体应力,grad(Q∈)为弹性波作用下流固耦合关系对固体的作用力,grad(ΦPff)为初始渗流压力对固体的作用力,grad(ΦPfs)=grad(Qe+R∈)为弹性波作用下流固耦合关系对流体的作用力;孔隙流体运动即广义达西方程,控制体元中运动流体流出流入的动量变化率等于所有有效作用外力的总和,右侧第一项为流固耦合作用下的流体惯性力,右侧第二项为流体在多孔介质中的达西渗流阻力。
| $\begin{gathered} \mu {\nabla ^2}u + {\text{grad}}\left[{\left( {\lambda + \mu } \right)e + Q \in } \right] + {\text{grad}}\left( {\phi {P_{{\text{ff}}}}} \right) = \hfill \\ \frac{{{\partial ^2}}}{{\partial {t^2}}}\left( {{\rho _{11}}u + {\rho _{12}}U} \right) - {\text{grad}}\left( {\phi {P_{\text{f}}}} \right) = \hfill \\ {\text{grad}}\left( { - \varphi {P_{{\text{ff}}}} + Qe + R \in } \right) = \frac{{{\partial ^2}}}{{\partial {t^2}}}\left( {{\rho _{12}}u + {\rho _{22}}U} \right) - {\text{grad}}\left( {{P_{\text{f}}}} \right) = \hfill \\ {\rho _{\text{f}}}\left( {\frac{{{\partial ^2}u}}{{\partial {t^2}}} + \frac{1}{\varphi }\frac{{{\partial ^2}U}}{{\partial {t^2}}}} \right) + \frac{\eta }{k}\frac{{\partial U}}{{\partial t}} \hfill \\ \end{gathered} $ | (10) |
液相连续性方程,即流体质量守恒方程,单位体积流体流入流出量之和等于单位时间内孔隙内流体质量变化率,
| ${\text{div}}\left[{{\rho _{\text{f}}}\frac{\partial }{{\partial t}}\left( {\frac{U}{\varphi } + u} \right)} \right] + \frac{\partial }{{\partial t}}\left( {{\rho _{\text{f}}}\varphi } \right) = 0$ | (11) |
根据Biot传播模型形变量、孔隙度和孔隙压力的关系(假设微粒在介质中剥离运移但未流出时,此处仅考虑波动条件下的孔隙变形),物性方程为
| ${\text{d}}\varphi {\text{ = }}\alpha {\text{d}}e + \frac{{{\text{d}}{P_{\text{f}}}}}{Q}$ | (12) |
流体粘度为[14]
| $\eta \left( \omega \right) \approx {\eta _0}\frac{{a\left( {1 + i} \right)}}{{4\sqrt 2 }}{\left( {\frac{{\omega {\rho _{\text{f}}}}}{\eta }} \right)^{0.5}}$ | (13) |
ω为高频时,由此得到液体在弹性波作用下的流动速度${v_w} = \frac{\partial }{{\partial t}}\left( {U - u} \right)$。
式中:u和U分别为固体位移、流体相对位移;ρ11、ρ12和ρ22为Biot模型中的耦合密度,其中ρs=ρ11+ρ12、ρf=ρ12+ρ22;e为岩石的体积应变;Pf为流体压力,Pff为初始渗流压力,Pfs为弹性波引起的流体压力变化,且Pf=Pff+Pfs;φ为多孔介质的孔隙度;k为多孔介质的渗透率;∈为流体的胀缩率;λ和μ为多孔介质拉梅系数,其中$\lambda = \frac{{Ev}}{{\left( {1 + v} \right)\left( {1 - 2v} \right)}},\mu = \frac{E}{{2\left( {1 + v} \right)}}$;Q和R为反映流固耦合关系的系数;α为多孔弹性介质有效压力的剪切当量;η为流体粘度;ω为振动频率。
3.2 微粒剥离运移捕集运动方程根据波动解堵技术对微粒剥离、运移、沉积的影响过程,剥离的微粒本身在液相中,因此不考虑粘土膨胀、盐溶解等过程,弹性波作用下固体微粒剥离、沉积、运移的质量守恒方程为
| $\begin{gathered} \frac{\partial }{{\partial x}}\left\{ {{v_w}\left[{{\rho _w}\left( {1 - {C_{\text{p}}}} \right) + {\rho _{\text{s}}}{C_{\text{p}}} + {\rho _{\text{s}}}{C_{\text{p}}}} \right]} \right\} = \hfill \\ \frac{\partial }{{\partial t}}\left\{ {\varphi \left[{{\rho _w} + \left( {{\rho _{\text{s}}} - {\rho _w}} \right)\left( {{C_{\text{p}}} + {g_{\text{b}}} - {g_{\text{d}}} - {g_{\text{p}}}} \right)} \right]} \right\} \hfill \\ \end{gathered} $ | (14) |
式中:Cp(r,t)r=rw=0,Cp(r,t)t=0=0。
当考虑孔喉内部可溶蚀盐类离子存在较多时,微粒剥离中需考虑盐离子的浓度方程变化(盐粒子在地层中运移的连续性方程是对流—扩散方程),
| $\varphi \frac{{\partial {C_{\text{S}}}}}{{\partial t}} + {v_w}\frac{{\partial {C_{\text{S}}}}}{{\partial x}} - \frac{\partial }{{\partial x}}\left( {\phi D\frac{{\partial {C_{\text{S}}}}}{{\partial x}}} \right) = 0$ |
式中:$x = 0,{v_w}{C_{\text{S}}} - \varphi D\frac{{\partial {C_{\text{S}}}}}{{\partial x}} = {v_{w,in}}{C_{S,in}};x = L,\frac{{\partial {C_{\text{S}}}}}{{\partial x}} = 0;t = 0,{C_{\text{S}}} = {C_{{\text{S0}}}}$。
对于存在粘土膨胀的情形,根据Fick第二定律,单位岩石体积内粘土吸附液体的质量速率为[17, 18]
| $\begin{gathered} {g_{sw}} = \lambda \beta \left( {{\rho _s} - \frac{{\rho pf}}{{{\rho _w}}} - \frac{{{\rho _{\text{s}}}{\rho _{lso}}}}{{{\rho _w}}}} \right){t^{ - 0.5}},其中 \hfill \\ \beta = \left\{ \begin{gathered} \beta '\left( {1 - {e^{{U_{cr}} - U}}} \right),U > {U_{{\text{cr}}}} \hfill \\ 0,U \leqslant {U_{{\text{cr}}}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ |
微粒在孔隙表面被剥离的速率,参考孙辉等[19]在弱疏松砂岩中的剥离液化砂方程,
| ${g_b} = \xi \left( {1 - \varphi } \right)\left( {{C_{\text{p}}} - \frac{{C_{\text{p}}^{\text{2}}}}{{{C_{{\text{cr}}}}}}} \right)R_{{\text{ch}}}^2{v_w}$ | (15) |
对于完全胶结且胶结强度较高的孔隙类型,假设原有孔喉充填物为被剥离、运移的微粒,则胶结物的含量和类型决定了剥离的速度,随着时间的增加,波动条件下被剥离充填物的数量呈指数下降,这与原有胶结物数量和接触面积有关,同时,还受到流速、孔隙度、渗透率、振动解堵前初始表皮因子等的影响,令
| ${g_{\text{b}}} = \frac{{{A_{cc}}{S_0}\left( {{g_{b0}} - {g_{b\infty }}} \right)}}{{1 - {\varphi _0}}}\exp \left( { - {\varphi _{{\text{ce}}}}{v_w} \cdot t} \right),\left| {{F_n}} \right|{\text{ > }}0$ | (16) |
对于不同应用环境中的微粒沉积速率,许多文献进行了表示[5, 9, 20],微粒孔隙表面沉积滞留的净速率为沉积速率和再释放速率的差值,可表示为
| $\frac{{\partial {g_{\text{d}}}}}{{\partial t}} = \left\{ \begin{gathered} A{v_w}{C_{\text{p}}},{v_w} \leqslant {v_{{\text{dcr}}}} \hfill \\ A{v_w}{C_{\text{p}}} - B{g_{\text{d}}}\left( {{v_w} - {v_{{\text{dcr}}}}} \right),{v_w}{\text{ > }}{v_{{\text{dcr}}}} \hfill \\ \end{gathered} \right.$ | (17) |
微粒在喉道处堵塞而导致的滞留速率方程用线性方程表示
| $\frac{{\partial {g_{\text{p}}}}}{{\partial t}} = \lambda {v_w}{C_{\text{p}}}$ | (18) |
式中:Cp为流体中微粒的体积浓度;gb、gD、gp分别为单位体积岩石中微粒从孔隙表面剥离的速率、微粒在孔隙表面沉积的速率、微粒在孔喉处堵塞而滞留的速率;ξ为出砂系数;Ccr为液化砂临界浓度;q为孔隙流体渗流量;Φce为孔隙中胶结物的比例,充填物疏松时Φce接近1,充填物较为致密且孔喉充填物数量较小时Φce?1;gb0为初始粒径较小充填物的剥离速度;gb∞为经长时间冲刷时初始粒径较小充填物的最终剥离速度,接近0,此时充填物基本无法再被剥离;S0为弹性波作用前初始表皮因子;Ace为微粒剥离相关的系数;A为表面沉积速度常数;B为挟带速率常数;vdcr为临界速率;λ为孔喉堵塞速率常数;D为盐离子在水相中的扩散系数,Cs为水相中的盐离子体积浓度;β′为液体吸附速率常数;Ucr为产生水化膨胀的临界侵入液累积孔隙体积;ρPf为悬浮中固相粒子的质量体积分数。
3.3 储层物性变化方程由于波动解堵技术作用,储层物性包括孔隙度、渗透率、表皮因子均发生变化[21],其中孔隙度变化为δΦ=gb-gD-gp,瞬时孔隙度为Φ=Φ0(1+δΦ);岩石物理分析中孔隙度和渗透率变化一般符合指数规律,渗透率的变化为$\frac{k}{{{k_0}}} = {\left[{\left( {1 - f} \right)D + f\frac{\phi }{{{\phi _0}}}} \right]^n}z{r_w} \approx {\left( {\frac{\phi }{{{\phi _0}}}} \right)^n}$,其中指数n约接近3。式中:k为绝对渗透率;k0为初始绝对渗透率;D为己堵塞孔隙允许流体渗流的常数;f为流动效率因子;z为常数;rD为污染损害半径;rw为井筒半径。
3.4 方程求解模型方程及其定解条件的精确解一般无法得到,通常只能计算其数值解。模型的求解一般由下述步骤组成:确定体系的物理参数;根据具体问题的条件,判定影响和控制微粒沉积、分散和运移的主导力学因素;确定微粒沉积、分散、运移引起渗透率下降的主要机理;建立模型;求解微粒沉积、分散、运移动力学的偏微分方程定解问题。针对微粒运移的非线性偏微分方程组,求解的方法包括有限差分法、有限元法、Monte-Carlo模型求解方法、分形理论模型求解方法、等效介质理论求解方法等[9, 22]。
4 弹性波作用下微粒运移对储层物性的影响弹性波作用下储层微粒运移模型与常规注入流体引起储层伤害的微粒运移模型不同在于,微粒来源于多孔介质中内部本身,因此,微粒被剥离后才能影响后续的运移与捕集。弹性波对储层微粒运移作用的影响变好或变差,取决于微粒运移后原有孔喉内的微粒降低量以及微粒运移距离、运移后的沉积/堵塞情况等。原有孔喉内的微粒降低量越大,即剥离量越大,孔隙介质渗透性变好;离注采井源汇点的微粒运移距离越大,表皮因子降低越大;运移后的沉积带内均匀分布,则沉积带渗透性越好;沉积带形成砂堵越严重,则沉积带渗透性越差,这取决于原有孔喉和运移微粒的尺寸对比。
由微粒剥离释放速率、微粒在孔隙表面沉积滞留的速率、微粒导致喉道堵塞而滞留的速率方程可知,弹性波作用下流速增加后,微粒剥离释放增加,但释放速度随着波衰减和时间延长而降低,微粒净沉积速率先上升后下降,当波动流速超过沉积净速率的临界值时出现拐点,同时,喉道堵塞速率有所上升。反映了弹性波作用下,微粒的悬浮能力增加,但是流速过大时,亦增加了微粒间相互碰撞导致在微细孔喉“架桥”堵塞的可能性,这也使储层进行波动解堵时出现部分井渗透性反而下降的状况。
由室内实验和矿场试验亦证实,振动参数和振动能量对微粒运移亦会造成影响。波动压力解堵时,存在最佳的频率和振幅。在一定的频率和振幅范围内,频率和振幅越大,微粒获得的波动能量越大,运动速度越快,运移距离越远;流速越大,微粒从流体中获得的能量越大,运动距离越远;微粒尺寸越小,沉积动力越小,运动越易维持。波动压力振幅是微粒侵人储层孔隙结构深部的主要外部原因。波动压力能使微粒处于不停波动状态,能使沉积的微粒再度运动。微粒的运动形式除了与岩石孔壁碰撞、滚动之外,还能随波动频率左右摆动前进。“空化现象”是解堵、除垢的一个强有力的有效手段[6],在声频范围内的一定频率下能产生“空化”,压力急剧波动使得微粒发生松动,“空化”的降黏效果亦增强了微粒运移的可能性和振动解堵的效果。
5 结论1)弹性波作用下多孔介质微粒剥离、分散、沉积过程受到影响,由于微粒剥离使得储层原有渗流状况发生改变,剥离后的微粒继而影响后续的运移与捕集。影响微粒剥离的临界速度公式显示,当微粒与孔喉半径的比值越小时,粘滞力所占比重越小,而弹性波导致的振荡附加力影响越大。
2)弹性波作用下微粒运移过程的变化,使建立的弹性波对储层微粒运移作用模型需要同时考虑弹性波作用下多孔介质渗流影响模型和微粒剥离-运移-捕集模型,但模型较为复杂,只能通过数值方法进行模拟求解。
3)弹性波作用下,微粒剥离释放速率、微粒在孔隙表面沉积滞留的速率、微粒导致喉道堵塞而滞留的速率发生改变。微粒的悬浮能力增加,但亦增加了微粒在微细孔喉“架桥”堵塞的可能性。
| [1] | 冯其红,韩晓冬,王守磊,等.注入水中悬浮微粒导致储层伤害网络模拟研究[J].西南石油大学学报(自然科学版),2014,36(3):179-184. Feng Qihong, Han Xiaodong, Wang Shoulei, et al. Network simulation of formation damage due to suspended particles in injection water[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2014,36(3):179-184. (in Chinese)( 1) 1) |
| [2] | 刘东,李丽,周承诗,等.注聚区油井防砂层堵塞原因与解堵措施[J].中国石油大学学报(自然科学版),2010,34(2):78-82. LIU Dong, LI Li, Zhou Chengshi, et al. Plugging mechanism and plug removing of sand control area in polymer injection well[J]. Journal of the China University of Petroleum, 2010, 34(2):78-82. (in Chinese)( 1) 1) |
| [3] | Abbasi S, Shahrabadi A, Golghanddashti H. Experimental investigation of clay mineral' effects on the permeability reduction in water injection process in the oil fields[C]//SPE European Formation Damage Conference. Noordwijk:Society of Retroleum Engineers, 2011:1-10.( 1) 1) |
| [4] | Ju B, Fan T. Experimental study and mathematical model of nanoparticle transport in porous media[J]. Powder Technology, 2009, 192(2):195-202.( 1) 1) |
| [5] | Zhang W, Morales V L, Cakmak M E, et al. Colloid transport and retention in unsaturated porous media:effect of colloid input concentration[J]. Environmental Science & Technology, 2010, 44(13):4965-4972.( 2) 2) |
| [6] | 蒋华义,赵松,赵贤明.压力波动条件下微粒运移规律的实验研究[J].钻采工艺,2005,28(4):70-73. JIANG Huayi, ZHAO Song, ZHAO Xianming. Experimental study on particle motion law under the condition of pressure wave[J]. Drilling & Production Technology, 2005, 28(4):70-73. (in Chinese)( 2) 2) |
| [7] | 李会平,陈现华,李良川,等.疏松砂层微粒运移特征及对油井动态的影响[J].断块油气田,1996,3(6):31-34. LI Huiping, Chen Xianhua, LI Liangchuan, et al. Particle migration character of unconsolidated reservoir and its influence on oil performance[J]. Fault-block Oil & Gas Field, 1996, 3(6):31-34. (in Chinese)( 1) 1) |
| [8] | 聂向荣,杨胜来,章星,等.颗粒尺度下砂岩出砂几何约束条件及毛管束模型[J].科技导报,2014,32(6):54-58. NIE Xiangrong, YANG Shenglai, ZHANG Xing, et al. Geometrical constraints and capillary bundle model for sand production in sandstone reservoir at particle scale[J].Science & Technology Review, 2014, 32(6):54-58. (in Chinese)( 2) 2) |
| [9] | 蒲春生.液-固体系微粒表面沉积分散运移微观动力学[M].北京:石油工业出版社,2008:52-79. PU Chunsheng. Micro-kinetics of particle deposition, dispersion and migration on the surface of the liquid-solid system[M]. Beijing:Petroleum Industry Press, 2008:52-79. (in Chinese)( 3) 3) |
| [10] | Panfilov M, Panfilova I, Stepanyants Y. Mechanisms of particle transport acceleration in porous media[J]. Transport in Porous Media, 2008, 74(1):49-71.( 1) 1) |
| [11] | 蒲春生,饶鹏,许洪星,等.大功率超声波近井无机垢解堵的动力学机理研究[J].重庆大学学报,2011,34(4):47-52. PU Chunsheng, RAO Peng, XU Hongxing, et al. Kinetic mechanism of inorganic scale plugging removal at near wellbore zone by high power ultrasonic technology[J]. Journal of Chongqing University, 2011, 34(4):47-52. (in Chinese)( 1) 1) |
| [12] | Bedrikovetsky P, Siqueira F D, Furtado C A, et al. Modified particle detachment model for colloidal transport in porous media[J]. Transport in Porous Media, 2011, 86(2):353-383.( 2) 2) |
| [13] | Rahman S S, Arshad A, Chen H. Prediction of critical condition for fines migration in petroleum reservoirs[M]. Society of Petroleum Engineers, 1994.( 1) 1) |
| [14] | Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid, Ⅱ:higher-frequency range[J]. Journal of the Acoustical Society of America, 1956, 28(2):179-191.( 2) 2) |
| [15] | Jakobsen M, Chapman M. Unified theory of global flow and squirt flow in cracked porous media[J]. Geophysics, 2009, 74(2):65-76.( 1) 1) |
| [16] | 刘静,蒲春生,刘涛,等.脉冲波作用下地层流体渗流规律研究[J].西安石油大学学报(自然科学版),2011,26(4):46-49. LIU Jing, PU Chunsheng, LIU Tao, et al. Study on the seepage law of formation fluid under the effect of pulse wave[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2011, 26(4):46-49. (in Chinese)( 1) 1) |
| [17] | 刘应学,李淑廉,黄鹤.钻井泥浆对储层损害的理论预测模型[J].江汉石油学院学报,1993,15(1):68-77. LIU Yingxue, LI Shulian, HUANG He. Theoretical models forecasting the formation impairment induced from drilling fluid[J]. Journal of Jianghan Petroleum Institute, 1993, 15(1):68-77. (in Chinese)( 1) 1) |
| [18] | 王松,胡三清,罗觉生.预测钻井完井液对油气层损害的数学模型[J].钻采工艺,2002,25(5):80-83. WANG Song, HU Sanqing, LUO Juesheng. Mathematical models forecasting the formation impairment induced from drilling fluid[J]. Drilling & Production Technology, 2002, 25(5):80-83. (in Chinese)( 1) 1) |
| [19] | 孙辉,李兆敏,马丕梁,等.弱胶结油藏拟三维出砂预测模型及方法[J].辽宁工程技术大学学报(自然科学版),2008,27(4):526-528. SUN Hui, LI Zhaomin, MA Pilang, et al. Pseudo-three-dimensional model and procedures for sand prediction in weakly consolidated reservoirs[J]. Journal of Liaoning Technical University (Natural Science), 2008, 27(4):526-528. (in Chinese)( 1) 1) |
| [20] | 张兴德.高含硫气藏硫沉积预测热力学模型[J].西安石油大学学报(自然科学版),2009,24(2):51-53. ZHANG Xingde. Thermodynamics model for predicting the sulfur deposition in the gas reservoirs of high H2S content[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2009, 24(2):51-53. (in Chinese)( 1) 1) |
| [21] | 鞠斌山,马明学,邱晓燕.弹性多孔介质粘土膨胀和微粒运移的数学模拟方法[J].水动力学研究与进展A辑,2003,18(1):8-15. JU Binshan, MA Mingxue, QIU Xiaoyan. The mathematical simulation method of migration of fines and clay swell in elastic porous medium[J]. Journal of Hydrodynamics, 2003, 18(1):8-15. (in Chinese)( 1) 1) |
| [22] | 曾流芳,刘建军,裴桂红.疏松砂岩油层出砂问题的Monte-Carlo模拟[J].钻井液与完井液,2002,19(3):10-13. ZENG Liufang, LIU Jianjun, PEI Guihong. Monte-Carlo simulation of sand production in unconsolidated sandstone oil reservoir[J]. Drilling Fluid and Completion Fluid, 2002, 19(3):10-13. (in Chinese)( 1) 1) |
 2016, Vol. 39
2016, Vol. 39

