由于集气管压力系统是一个具有高度非线性、扰动变化激烈且幅值大的多变量耦合系统[1],因此,难以用常规方法控制。近年来,国内外对集气管压力系统进行了大量的理论和实践研究,如文献[2]提出PID控制、前馈控制和专家控制相结合的混合控制方法控制集气管压力,具有较强的抗干扰能力;文献[3]采用模型预测控制(MPC)对集气管压力系统进行解耦设计,一定程度上解决了耦合问题;文献[4]采用动态矩阵控制(DMC)方法对多变量集气管压力系统进行控制,具有一定的可行性和有效性。由于集气管压力系统的复杂性,上述方法虽然起到一定的调节作用,但对于多变量耦合、各种复杂工况和干扰的问题仍未得到很好地解决。
随着智能控制技术的发展,最小二乘支持向量机(LS-SVM)α阶逆系统方法由于优点突出已成功应用于非线性系统控制中[5, 6, 7]。与神经网络逆解耦方法存在过学习、局部极点小、结构过分依赖经验等缺陷[8]相比,最小二乘支持向量机方法利用其泛化能力[9],极大提高了训练效率[10],明显优于神经网络等传统方法。非线性内模控制对干扰和模型失配都有良好的鲁棒性[11, 12],将内模控制用来抑制干扰和弥补模型失配将起到良好的控制效果[13]。
根据焦炉集气管压力系统可逆[14],研究首先建立系统的低阶线性模型和非线性未建模动态项。针对这样一个非线性动态系统,采用最小二乘支持向量机辨识集气管压力系统的α阶逆系统模型串联在原系统之前构成伪线性系统以实现解耦。为保证控制系统的鲁棒性,采用内模控制进行系统综合。最后通过仿真试验验证了所设计控制方法的有效性,并成功应用于某焦化厂焦炉集气管压力系统的控制。
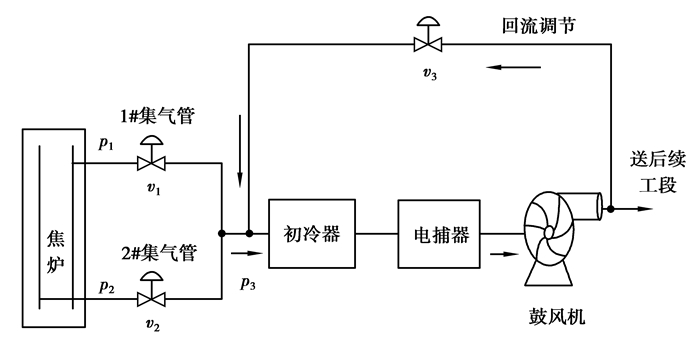
1 焦炉集气管压力系统工艺过程描述与建模 1.1 集气管压力系统工艺过程某焦化厂焦炉集气管压力系统如图 1所示。焦炉有2个集气管,呈不对称分布,产生的荒煤气经2个集气管汇入总管,通过初冷器冷却后,一部分经鼓风机抽送外供,另一部分经回流管回到初冷器前的总管。集气管压力控制系统以压力p1,p2为被控量,蝶阀开度v1,v2为控制量,通过控制2个蝶阀开度来使压力保持在正常范围内,即120±20 Pa。
|
图1 焦炉集气管压力系统结构 Fig. 1 Structure of gas collector pressure in coke ovens |
在实际生产中,由于推焦、加煤、出焦以及喷洒高压氨水等操作,集气管压力会发生剧烈波动。同时,由于焦炉之间的不对称分布,导致管道的布线联接方式不同,使得焦炉各集气管之间存在严重的耦合影响。综上所述,焦炉集气管压力系统是一个多变量耦合、非线性和强干扰的复杂系统。
1.2 系统模型建立研究将集气管压力系统非线性模型分解为2部分:低阶线性模型和非线性未建模动态项。其中低阶线性部分采用基于ARX模型的最小二乘法辨识得到,非线性未建模动态项采用支持向量机辨识得到。
对于较一般的非线性离散系统[15],假设其输入和输出都是p维,其输入输出差分方程一般可表示为
| $f\left[{y\left( {k + r} \right),{y_\Sigma },u\left( k \right),{u_\Sigma }} \right]$ | (1) |
式中:f[·]为未知的非线性函数。
| $\begin{gathered} y = \left( {k + r} \right) = {\left[{{y_1}\left( {k + {r_1}} \right),{y_2}\left( {k + {r_2}} \right),\cdots ,{y_p}\left( {k + {r_p}} \right)} \right]^{\text{T}}},\hfill \\ u\left( k \right) = {\left[{{u_1},{u_2},\cdots ,{u_p}} \right]^{\text{T}}},\hfill \\ {y_\Sigma } = {\left[{{y_1},{y_2},\cdots ,{y_i},\cdots ,{y_p}} \right]^{\text{T}}},\hfill \\ {y_i} = {\left[{{y_i}\left( {k + {r_i} - 1} \right),{y_i}\left( {k + {r_i} - 2} \right),\cdots ,{y_i}\left( {k + {r_i} - {n_i}} \right)} \right]^{\text{T}}},\hfill \\ {u_\Sigma } = {\left[{{u_1},{u_2},\cdots ,{u_i},\cdots ,{u_p}} \right]^{\text{T}}},\hfill \\ {u_i} = {\left[{{u_i}\left( {k - 1} \right),{u_i}\left( {k - 2} \right),\cdots ,{u_i}\left( {k - {m_i}} \right)} \right]^{\text{T}}},i = 1,2,\cdots ,p \hfill \\ \end{gathered} $ |
式中:r=[r1,r2,…,rp]为输出y相对输入u的时延,一般情况下ri>0(i=1,2,…,p)。
复杂工业过程可以分解为低阶线性模型和非线性未建模动态项[16]。因此可以将集气管压力系统模型转化为以下形式
| $A\left( {{z^{ - 1}}} \right)y\left( k \right) = B\left( {{z^{ - 1}}} \right)u\left( k \right) + v\left[{x\left( k \right)} \right]$ | (2) |
式中:y(k)为集气管压力第k采样时刻的输出信号;u(k)为集气管第k采样时刻蝶阀开度,v[x(k)]为未建模动态项。
| $\begin{gathered} A\left( {{z^{ - 1}}} \right) = {I_n} + {A_1}{z^{ - 1}} + {A_2}{z^{ - 2}} + \cdots + {A_n}{z^{ - n}},\hfill \\ B\left( {{z^{ - 1}}} \right) = {B_1}{z^{ - 1}} + {B_2}{z^{ - 2}} + \cdots + {B_n}{z^{ - n}},\hfill \\ x\left( k \right) = {\left[{{x_1},{x_2},\cdots ,{x_i},\cdots ,{x_p}} \right]^{\text{T}}} \hfill \\ \end{gathered} $ |
xi=[yi(k),yi(k-1),…,yi(k-n+1),ui(k),ui(k-1),…,ui(k-m)],m和n分别是系统输入和输出多项式的阶次。
1.2.1 线性模型的辨识集气管压力系统模型(2)中的线性部分如下
| $A\left( {{z^{ - 1}}} \right)y\left( k \right) = B\left( {{z^{ - 1}}} \right)u\left( k \right)$ | (3) |
根据现场对集气管压力系统调研发现,该系统在正常工况下运行特性满足一阶被控对象的特征,因此可以等效为一阶被控对象。该系统的ARX辨识模型差分方程形式如下
| $\left[\begin{gathered} {y_1}\left( k \right) \hfill \\ {y_2}\left( k \right) \hfill \\ \end{gathered} \right] = {A_1}\left[\begin{gathered} {y_1}\left( {k - 1} \right) \hfill \\ {y_2}\left( {k - 1} \right) \hfill \\ \end{gathered} \right] + {B_1}\left[\begin{gathered} {u_1}\left( {k - 1} \right) \hfill \\ {u_2}\left( {k - 1} \right) \hfill \\ \end{gathered} \right]$ | (4) |
A1,B1均为2×2矩阵,且均为待辨识参数;u1(k-1)为1#集气管蝶阀开度第k-1采样时刻控制信号;y1(k)为1#集气管压力第k采样时刻输出信号;u2(k-1)为2#集气管蝶阀开度第k-1采样时刻控制信号;y2(k)为2#集气管压力第k采样时刻输出信号。
为使辨识出的模型能更好的反应和体现集气管压力系统运行状况特性,从现场采集正常运行状况下的300组数据辨识模型。由于现场采集到的数据存在大量的不可使用的数据,使用Matlab工具箱中的dtrend函数来剔除数据信号中的高频数据。其基本调用格式如下
| $\left\{ \begin{gathered} zd = {\text{dtrend}}\left( {z,o,brkp} \right),\hfill \\ z = \left[{yu} \right] \hfill \\ \end{gathered} \right.$ | (5) |
其中o代表趋势项的阶次,取其值为0;brkp用于包含分段线性趋势数据,取brkp=0。
最终利用最小二乘法辨识得到输入/输出模型如下
| $\begin{gathered} \left[\begin{gathered} {y_1}\left( k \right) \hfill \\ {y_2}\left( k \right) \hfill \\ \end{gathered} \right] = \left[\begin{gathered} 0.1304{\text{ }}0 \hfill \\ {\text{ }}0{\text{ }}0.118 \hfill \\ \end{gathered} \right]\left[\begin{gathered} {y_1}\left( {k - 1} \right) \hfill \\ {y_2}\left( {k - 1} \right) \hfill \\ \end{gathered} \right] + \left[\begin{gathered} 2.53{\text{ }}0.7339 \hfill \\ 0.49{\text{ }}1.55 \hfill \\ \end{gathered} \right] \hfill \\ \left[\begin{gathered} {u_1}\left( {k - 1} \right) \hfill \\ {u_2}\left( {k - 1} \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} $ | (6) |
当集气管压力发生变化时,固定线性模型(6)不变,将集气管压力变化部分归属于未建模动态项v[x(k)]。研究利用基于支持向量机逼近非线性部分v[x(k)]。将控制量u(k)作用于实际对象上可得到压力的实际输出y(k+1),同时将控制量u(k)作用于线性模型(6)可得到输出$\hat y$(k+1),由此得到式(2)中非线性部分v[x(k)]为
| $v\left[{x\left( k \right)} \right] = y\left( {k + 1} \right) - \hat y\left( {k + 1} \right)$ | (7) |
支持向量机的输入x(k)=[x1,x2,…,xi,…,xp]T,xi=[yi(k),yi(k-1),…,yi(k-n+1),ui(k),ui(k-1),…,ui(k-m)],i=1,2,…,p,输出为v[x(k)]的逼近值$\hat v$[x(k)]。采集现场数据,并根据式(7)可得到支持向量机的期望输出数据,对支持向量机进行充分的离线训练。
综上所述,集气管压力系统的非线性模型为
| $\begin{gathered} \left[\begin{gathered} {y_1}\left( k \right) \hfill \\ {y_2}\left( k \right) \hfill \\ \end{gathered} \right] = \left[\begin{gathered} 0.1304{\text{ }}0 \hfill \\ {\text{ }}0{\text{ }}0.118 \hfill \\ \end{gathered} \right]\left[\begin{gathered} {y_1}\left( {k - 1} \right) \hfill \\ {y_2}\left( {k - 1} \right) \hfill \\ \end{gathered} \right] + \left[\begin{gathered} 2.53{\text{ }}0.7339 \hfill \\ 0.49{\text{ }}1.55 \hfill \\ \end{gathered} \right] \hfill \\ \left[\begin{gathered} {u_1}\left( {k - 1} \right) \hfill \\ {u_2}\left( {k - 1} \right) \hfill \\ \end{gathered} \right] + v\left[{x\left( k \right)} \right] \hfill \\ \end{gathered} $ | (8) |
| $v\left[{x\left( k \right)} \right] = \hat v\left[{x\left( k \right)} \right] + \zeta $ | (9) |
式中:$\hat v$[x(k)]为支持向量机的输出,ξ为支持向量机的逼近误差。
2 基于LS-SVMα阶逆系统方法的集气管压力系统解耦控制针对建立的非线性动态系统,采用最小二乘支持向量机辨识集气管压力系统的α阶逆系统模型,并将其串联在原系统之前以实现解耦,构成2个相互独立的集气管压力系统。
根据逆系统的原理可知其实现必须满足2个前提条件:1)原系统的数学模型准确可知;2)能从原系统的数学模型求得u(k)的显示表达式。然而这在实际应用中很难实现,因此采用最小二乘支持向量机辨识集气管压力系统的逆系统模型更有实用价值。
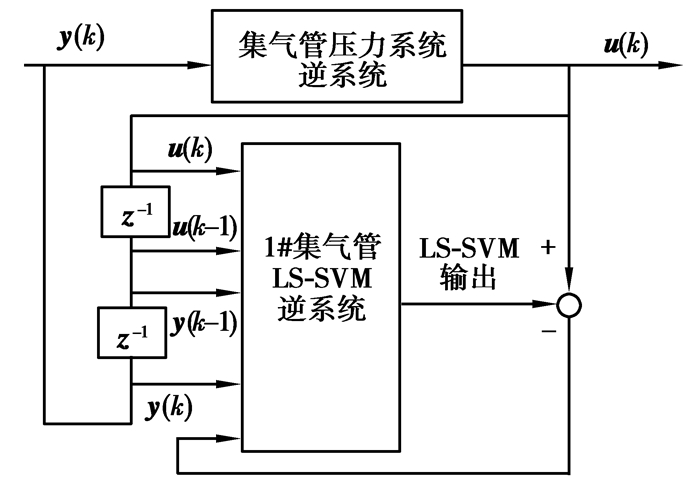
以1#集气管为例,采用结构辨识其逆系统,如图 2所示。
|
图2 LS-SVM辨识1#集气管逆系统的结构图 Fig. 2 The identification structure of 1# gas collector invert systerm based on LS-SVM |
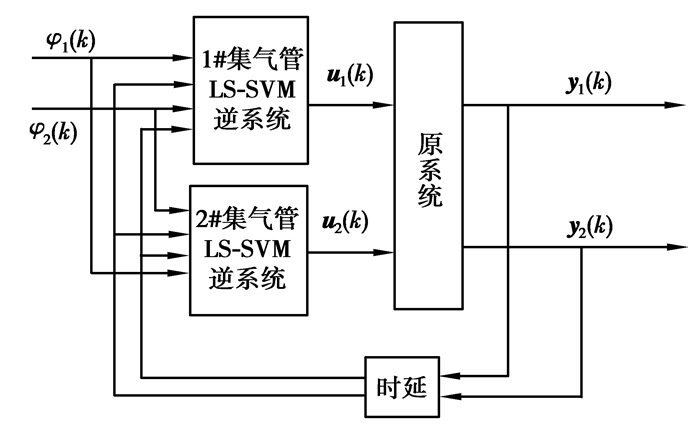
由于辨识得到的LS-SVM系统是单输出系统,为了实现多输入多输出系统的辨识,针对研究对象,需要设计2个相应的学习机,如图 3所示。
|
图3 集气管压力系统逆解耦控制结构 Fig. 3 The control structure of inverse decoupling for gas collector pressure in coke ovens |
重新定义输入φ(k)=y(k+α),即φ1(k)=y1(k+α),φ2(k)=y2(k+α)。通过给原系统施加激励信号,得到输入输出样本数据,Xij,uij(i=j=1,2),uij=uj(i)。通过对2个LS-SVM的学习,得到相应的输入向量系数αij(j=1,2)和阈值bj,根据当前的输入Xj(拟合因子),这里拟合因子可以由y(k+α),${y_\Sigma },{u_\Sigma }$组成。就可辨识出α阶逆模型的输出
| $\begin{gathered} {u^j}\left( k \right) = g\left[{{X^j}} \right] = \sum\limits_{i = 1}^d {\left( {{{\left( {\alpha _i^j} \right)}^ * } - \alpha _i^j} \right)\left( {\Phi \left( {X_i^j} \right)\Phi \left( {{X^j}} \right)} \right) + {b_j}} \hfill \\ \sum\limits_{i = 1}^d {\left( {{{\left( {\alpha _i^j} \right)}^ * } - \alpha _i^j} \right)K\left( {x_i^j{X^j}} \right) + {b^j}} \hfill \\ \end{gathered} $ | (10) |
式中:d是样本的数量,K(·,·)为核函数。将求得α阶逆系统串联在原系统之前,得到解耦的相互独立的2个伪线性子系统。
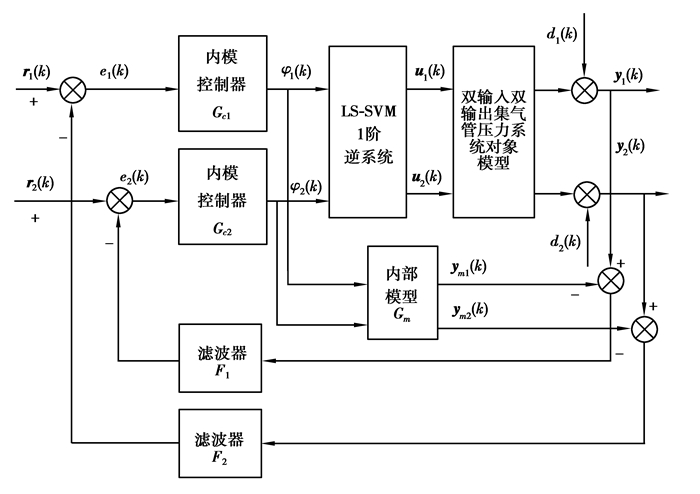
3 系统复合控制最后进行系统复合控制。使用LS-SVM很容易辨识得到原系统的(α=1)1阶逆系统,由于基于LS-SVM辨识得到的逆系统模型与实际系统存在建模误差,同时考虑到系统在运行过程中,外部干扰也会对系统存在影响,为此引入内模控制以改善系统的鲁棒性。如图 4所示。
|
图4 焦炉集气管压力系统内模解耦控制结构图 Fig. 4 The IMC decoupling control structure of gas collector pressure in coke ovens |
图中r1(k),r2(k)为1#,2#集气管压力设定值;y1(k),y2(k)为1#,2#集气管压力输出值;u1(k),u2(k)为1#,2#集气管压力伪线性子系统的输出值,即集气管蝶阀开度控制信号;φ1(k),φ2(k)为内模控制器1、内模控制器2的输出;d1(k),d2(k)为扰动输入。
由系统相对阶α=1,因此取内部模型为
| ${G_m}\left( z \right) = \left[\begin{gathered} \frac{1}{z}{\text{ }} \hfill \\ {\text{ }}\frac{1}{z} \hfill \\ \end{gathered} \right]$ | (11) |
内模控制器Gc1(z)=Gc2(z)=F1(z)Gm-1(z),滤波器${F_1}\left( z \right) = {F_2}\left( z \right) = {\text{diag}}\left\{ {\frac{{1 - {a_i}}}{{1 - {a_i}{z^{ - 1}}}}} \right\}$,i=1,2,取a1=a2=0.85。
4 系统实现及仿真结果利用从某焦化厂采集得到的300组现场正常工况下集气管压力与蝶阀开度的数据,其中200组数据用来对支持向量机网络进行训练,剩余的100组数据作为测试集。LS-SVM辨识逆系统时,采用核函数为多项式核函数K(x,xiT)=(xiTx+σ)d,其参数d=3,σ=1.2,规则化参数γ=1 000,拟合因子
| $\begin{gathered} {x_1} = \left[{{\varphi _1},{y_1}\left( {k - 1} \right),{u_1}\left( {k - 1} \right),{u_2}\left( {k - 1} \right)} \right],\hfill \\ {x_2} = \left[{{\varphi _2},{y_2}\left( {k - 1} \right),{u_1}\left( {k - 1} \right),{u_2}\left( {k - 1} \right)} \right],\hfill \\ \end{gathered} $ |
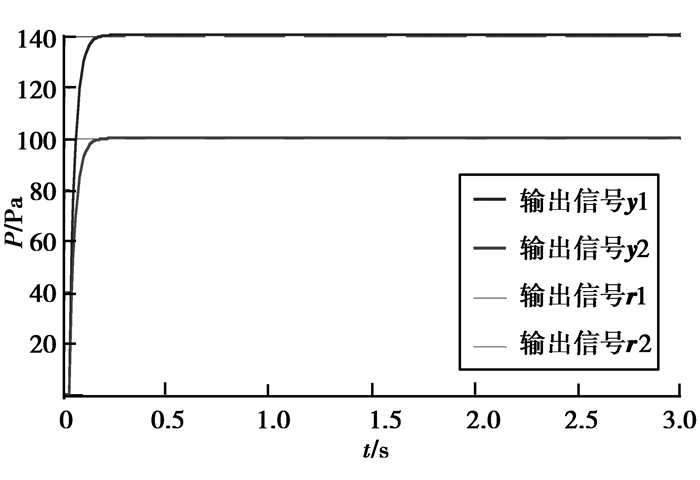
采样时间为0.01 s,仿真时间为3 s。为模拟焦炉车间现场的设定值,对解耦后的伪线性子系统输入R=[r1,r2]=[140,100]的信号,从图 5可以看出在伪线性子系统跟踪效果好,没有出现波动或耦合现象,表明实现了焦炉集气管压力系统的解耦,且具有很好的控制性能。
|
图5 集气管伪线性系统的跟踪 Fig. 5 Tracking of pseudo-linear systems for gas collector |
为证实复合控制的有效性,模拟焦炉车间现场的设定值,对于y1,在前150个采样点的设定值为100 Pa,在150到300个采样点之间的设定值为80 Pa;对于y2,在前150个采样点的设定值为120 Pa,在150~300个采样点之间的设定值为140 Pa。采样时间为0.01 s,仿真时间为3 s。对y1在k=40和170时,分别加入R=10 Pa和-50 Pa的干扰,模拟正常工况下的未知干扰和机后压力突降;对y2在k=100和220时,分别加入R=10 Pa和50 Pa的干扰,模拟正常工况下的未知干扰和高压氨水喷洒时的强干扰。
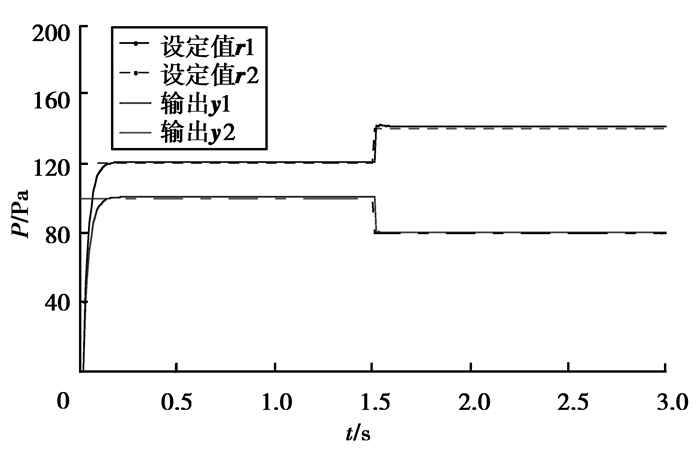
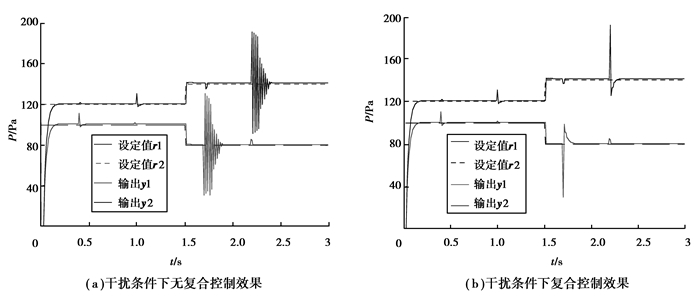
由图 6可知,复合控制在无干扰情况下,模型跟踪非常精确,在设定值切换时只有微小的波动,控制效果很好。由图 7(a)可知,无复合控制时,系统受到扰动后的超调量大,超调时间长。由图 7(b)可知,采用复合控制的系统虽然在扰动时产生了轻微的震荡,但较图 7(a),其产生的超调量较小,超调时间较短,且较为快速的将系统调节到稳定的范围。总的来说,设计的复合控制系统解耦控制效果较好,在正常工况下可以抑制未知较弱干扰,同时在非工况下,能快速的抑制强干扰引起的超调问题,适用于焦炉集气管压力系统的控制。
|
图6 无干扰条件下复合控制效果 Fig. 6 Result of compound controller without interference |
|
图7 干扰条件下有无复合控制的效果 Fig. 7 Results of compound controller and without compound controller under interference |
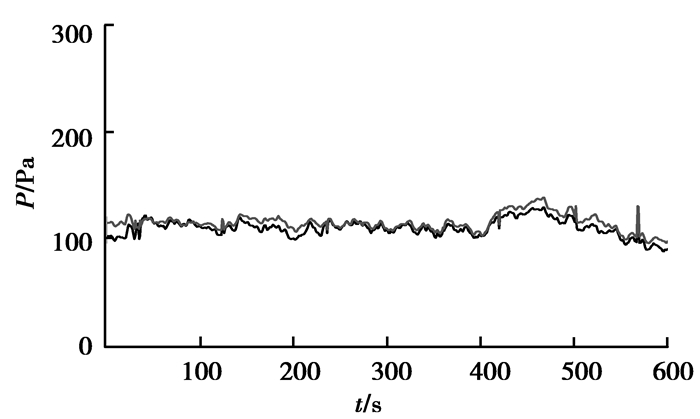
采用上述设计方案对某焦化厂集气管压力系统进行控制系统设计,由浙大中控的DCS完成对系统的软硬件设计。现场的一座焦炉有2个集气管,其正常工况下的变化曲线如图 8所示。
|
图8 1#2#集气管压力趋势图 Fig. 8 Trend chart of 1# 2# gas collector pressure |
集气管压力的设定值为120 Pa,根据工况变化,2集气管压力的高低及蝶阀的开度在-0.65~-0.8之间自动调节。从趋势图可以看出2集气管压力的变化满足现场工艺要求的波动范围,解耦效果较好。
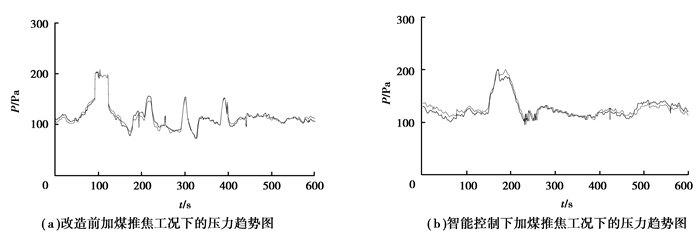
图 9是加煤推焦工况时,改造前后的压力趋势图比较。表明智能控制下系统具有较强的抗干扰能力,较为快速的抑制震荡并恢复平稳过程的能力。经过现场长时间观察,在焦炉开盖、关盖,以及煤气流量等因素引起压力波动时,系统能快速调节1#,2#集气管的蝶阀开度使集气管压力在20 s内达到稳定,保证压力稳定在120±20 Pa的范围。
|
图9 加煤推焦工况下集气管压力趋势图 Fig. 9 Trend chart of gas collector pressure under the condition of adding coal and coke pushing |
用LS-SVM辨识双输入双输出焦炉集气管压力系统的逆系统,对其进行动态解耦,并结合内模控制器设计闭环控制系统实现对焦炉集气管压力系统的控制。仿真及应用结果表明,实现了对焦炉集气管压力系统动态解耦控制,具有良好的控制效果。该方法将LS-SVM逆系统控制与内模控制结合,具有跟踪精度高、良好的抗干扰和抑制震荡的能力。同时其算法较简单,与现场软件对接问题容易解决,且操作易行。对于强耦合、非线性,不易求出精确数学模型的工业生产过程,该控制策略具有良好的应用价值和广阔的应用前景。
| [1] | 张世峰,周建芳.焦炉集气管压力自适应预测解耦控制系统设计[J].重庆大学学报,2009,32(1):105-109. ZHANG Shifeng, ZHOU Jianfang. A radial basis function neural network based self-adaption predictive decoupling control system for gas collector pressure in coke ovens[J]. Journal of Chongqing University, 2009, 32(1):105-109. (in Chinese)( 1) 1) |
| [2] | Yang C H, WU M, Shen D Y, et al. Hybrid intelligent control of gas collector of coke ovens[J]. Control Engineering Practice, 2001, 9(7):725-733.( 1) 1) |
| [3] | Li K, Li D W, Xi Y G, et al. Model predictive control with feedforward strategy for gas collectors of coke ovens[J]. Chinese Journal of Chemical Engineering, 2014, 22(7):769-773.( 1) 1) |
| [4] | Li K, Dong J, Jiang M L. Dynamic matrix control for multiple gas collectors of coke ovens[J]. Applied Mechanics and Materials, 2014, 599:1215-1219.( 1) 1) |
| [5] | 王正齐.无轴承异步电机非线性解耦控制策略研究[D].江苏:江苏大学,2011. WANG Zhengqi. Study on nonlinear decoupling control strategy of bearingless induction motor[D]. Jiangsu:Jiangsu University, 2011. (in Chinese)( 1) 1) |
| [6] | 刘国海,张懿,魏海峰,等.基于自抗扰控制器的两电机变频调速系统最小二乘支持向量机逆控制[J].中国电机工程学报,2012,32(6):138-144. LIU Guohai, ZHANG Yi, WEI Haifeng, et al. Least squares support machines inverse control for two-motor variable frequency speed-regulation system based on ac-tive disturbances rejection[J]. Proceedings of the CSEE, 2012, 32(6):138-144. (in Chinese)( 1) 1) |
| [7] | 郑恩辉,曹文浩,刘兆磊,等.基于多模型和 SVM 逆系统单元机组解耦控制[J].控制工程,2012,19(4):590-593. ZHENG Enhui, CAO Wenhao, LIU Zhaolei, et al. Decoupling control based on muti-model and SVM inversion in the Boiler-turbine Unit[J]. Control Engineering of China, 2012,19(4):590-593. (in Chinese)( 1) 1) |
| [8] | 孙晓东,朱熀秋.基于神经网络逆系统理论无轴承异步电动机解耦控制[J].电工技术学报,2010, 25(1):43-49. SUN Xiaodong, ZHU Huangqiu. Decoupling control of bearingless induc-tion motors based on neural network inve-rse system method[J]. Transactions of China Electrotechnical Society, 2010, 25(1):43-49. (in Chinese)( 1) 1) |
| [9] | Sinapov J, Sukhoy V, Sahai R, et al. Vibrotactile recognition and categorization of surfaces by a humanoid robot[J]. IEEE Transactions on Robotics, 2011, 27(3):488-497.( 1) 1) |
| [10] | 朱熀秋,曹莉,李衍超,等.基于最小二乘支持向量机逆系统的五自由度无轴承同步磁阻电机解耦控制[J]. 中国电机工程学报,2013,33(15):99-108. ZHU Huangqiu, CAO Li, LI Yanchao, et al. Decoupling control of 5-degree of freedom bearingless synchronous reluctance motor based on least square support vector machine inverse system[J]. Proceedings of the CSEE, 2013, 33(15):99-108. (in Chinese)( 1) 1) |
| [11] | 郝晓弘,耿亮,麻圆圆,等. 动态补偿逆的非线性内模控制在机器人中的应用[J].自动化与仪表,2010,39(2):39-41. HAO Xiaohong, GEN Liang, MA Yuanyuan, et al. Application of non-linear internal model control based on dynamic compensation inverse in robot[J]. Automation & Instrumentation,2010, 39(2):39-41. (in Chinese)( 1) 1) |
| [12] | 雷靖,白雪玲.非线性系统全状态线性化内模扰动抑制[J].电子科技大学学报,2014,43(1):71-75. LEI Jing, BAI Xueling. Internal-Model disturbance rejection for nonlinear systems via-full-states linearization[J]. Journal of University of Electronic Science and Technology of China, 2014, 43(1):71-75. (in Chinese)( 1) 1) |
| [13] | Zhao Z C, Liu Z Y, Xia Z M, et al. Internal model control based on LS-SVM for a class of nonlinear process[C]//International Confernce on Solid State Devicesm and Materials Science. Macao:IEEE, 2012:1900-1908.( 1) 1) |
| [14] | 张世峰,左慧敏.焦炉集气管压力系统内模控制器设计[J].安徽工业大学学报(自然科学版),2014, 31(4):395-398. ZHANG Shifeng, ZUO Huimin. An internal model controller design for gas collector pressure in coke ovens[J]. Anhui University of Technology (Nature Science Edition), 2014, 31(4):395-398. (in Chinese)( 1) 1) |
| [15] | Hirschorn R M. Invertible of multivariable nonlinear control system[J]. IEEE trans on automatic control, 1979, 24(6):855-865.( 1) 1) |
| [16] | Zhai L F, Chai T Y. Intelligent decoupling PID control of a class of complex industrial processes[C]//Proceedings of the 6th World Congress on Intelligent Control and Automation. New York:IEEE, 2006:485-491.( 1) 1) |
 2016, Vol. 39
2016, Vol. 39


