2. 重庆大学煤矿灾害动力学与控制国家重点实验室, 重庆 400030;
3. 中石油川庆钻探公司 广汉钻采院, 四川 广汉 618300;
4. 武汉三江航天远方科技有限公司, 武汉 430030
2. State Key Laboratory of Coal Mine Disaster Dynamicsand Control, Chongqing University, Chongqing 400030, P. R. China;
3. Drilling EngineeringAcademy of Technology, Chuanqing Drilling Engineering Co., Ltd. of CNPC, Guanghan 618300, Sichuan, P. R. China;
4. Wuhan Sanjiang Hangtian Yuanfang TechnologyCo., Ltd., Wuhan 430030, P. R. China
蠕变作为岩石的一项重要力学性质与许多工程质量息息相关[1, 2],在油气钻井工程中,由岩石蠕变导致井眼缩径及井壁坍塌所造成的经济损失不可小觑。
国内外学者对岩石的蠕变特性做了大量的理论及实验研究[3, 4, 5, 6, 7]。Yang等[8]对高温-高含冰量冻结沙土蠕变行为进行了实验及理论研究;范翔宇等[9]对煤岩储气层岩石蠕变特性与本构模型进行了研究,建立了饱依丁汤姆逊体与宾汉姆体串联模型;杨逾等[10]建立了西原加速模型;Kang J等[11]建立了考虑损伤效应的煤岩非线性本构蠕变模型;李金和等[12]通过单轴压缩蠕变实验研究了大理岩本构蠕变模型参数;陈绍杰等[13]采用LS-DYNA 数值方法分析了深部煤柱的蠕变支撑效应;周长冰等[14]建立了高温三轴应力条件下的煤岩本构蠕变模型;赵斌等[15]对不同应力水平条件下煤岩蠕变破坏特征进行了研究;刘钦等[16]对灰质页岩蠕变特性进行了试验研究;杨红伟等[17]对三轴压缩条件下岩石孔隙水压力分级加载蠕变试验进行了研究;Gao等[18]建立了在温度和湿度影响下岩石的粘弹塑性本构蠕变模型; Zhou等[19]通过分数阶导数建立了岩盐本构蠕变模型。
以上理论和方法是从纯力学的角度研究了岩石的蠕变特性。拟从能量角度对油气钻井工程中钻遇岩石蠕变特性进行详细研究与分析,并且对西原模型进行改进,建立能够明显反映岩石加速蠕变阶段的岩石蠕变模型。
1 理论分析岩石蠕变通常分为2种形式,即衰减蠕变[20]和非衰减蠕变[21]。当岩石所受荷载小于长期强度时,岩石发生衰减蠕变;在岩石所受荷载大于长期强度时,岩石发生非衰减蠕变。
在油气井钻井过程中,很多井眼缩径或井壁坍塌是由岩石的非衰减蠕变引起的。从能量角度分析岩石非衰减蠕变的3个阶段为:1) 减速蠕变阶段。该阶段主要以弹性形变为主。其原因是岩石要破裂,首先要破坏各基元的价键。而岩石基元粒子之间是通过各种化学键相结合的,这些价键的结合力是吸引力和排斥力共同作用的结果。在此阶段,外力功主要转变为弹性势能(由于岩石先天性的缺陷,因此该阶段并非表现理想弹性体的特点)[22]。2) 稳定蠕变阶段。主要以塑性变形为主。其原因是岩石弹性势能达到一定程度,价键开始断裂,岩石的不同组元内开始大量产生各种缺陷,使得岩石所受的外力功主要转化为塑性变形能,故该阶段主要表现出塑性变形的特点[22]。3) 加速蠕变阶段。该阶段发展迅速,并且在短时间内发生破坏。主要是因为岩石在外力功的作用下,岩石内部积蓄的塑性变形能已经达到极限,岩石产生宏观裂纹并迅速扩展。在此阶段,外力功主要转化为动能,导致应变迅速增大,直至岩石破坏。
2 模型建立 2.1 西原模型西原模型是由胡克体、开尔文体和理想粘塑性体串联而成,其力学模型见图 1,能够较全面反映岩石的弹粘弹粘塑性特征[23]。

|
图 1 西原体力学模型 Fig. 1 Nishiharamodel |
模型中,当岩石所受荷载(σ)小于岩石的长期强度(σs)时,只有胡克体和开尔文体发生形变;当岩石所受荷载大于岩石长期强度时,将引起理想粘塑性体发生形变。
图 1中E1、E2分别为胡克体和开尔文体中的弹性模量;η1、η2分别为开尔文体和理想粘塑性体中的黏性系数。
该模型对应的蠕变方程为
1) 当σ0 < σs时,蠕变方程
| $\varepsilon = \frac{{{\sigma _0}}}{{{E_1}}} + \frac{{{\sigma _0}}}{{{E_2}}}\left[ {1 - \exp \left( { - \frac{{{E_2}}}{{{\eta _1}}}t} \right)} \right]. $ | (1) |
2) 当σ0≥σs时,蠕变方程
| $ \varepsilon = \frac{{{\sigma _0}}}{{{E_1}}} + \frac{{{\sigma _0}}}{{{E_2}}}\left[ {1 - \exp \left( { - \frac{{{E_2}}}{{{\eta _1}}}t} \right)} \right] + \frac{1}{{{\eta _2}}}\left( {{\sigma _0} - {\sigma _s}} \right)t, $ | (2) |
式中:ε为岩石应变,%;σ0为岩石所受荷载,MPa;t为时间,h。
2.2 改进西原模型从上述理论分析可知,在岩石的蠕变模型中,西原模型能够较好地研究大部分岩石的衰减蠕变过程,但是对于研究非衰减蠕变具有局限性。主要原因是西原模型的元件组成只能解释出岩石在外力功的情况下转变为弹性势能,塑性势能2个阶段,对于第3阶段,即外力功转换为动能阶段无法诠释。基于此,从能量角度改进西原模型来研究岩石的蠕变特性。
在不考虑岩石内部热交换的情况下,由能量守恒定律重点研究岩石蠕变的第3阶段,令M为岩石试件的质量(kg),L为试件的高度(mm),ε为轴向应变(%),υ为轴向变形速率(m/s),t为时间(s),σ为轴向荷载(MPa),S为岩石试件端部面积(mm2),ρ为试件密度(g/cm3),λ为修正系数,无量纲(λ > 1,其意义为外力功不可能完全转换为动能)。
取岩石试件在单位时间内的微元应变为Δε(%),应变速率为Δυ(m/s),根据功能关系推导出如下公式
| $ \left. \begin{array}{l} \sigma \bullet S \bullet L \bullet \Delta \varepsilon = \frac{1}{2}\lambda \bullet M{\left( {\Delta \upsilon } \right)^2}\\ \Delta \upsilon = \alpha t\\ \alpha = \frac{{\sigma \bullet S}}{{\rho \bullet S \bullet L}} \end{array} \right\} \Rightarrow \Delta \varepsilon = \frac{1}{2}\lambda \frac{\sigma }{{\rho {L^2}}}\left( {\Delta {t^2}} \right), $ | (3) |
对式(3)进行积分可得
| $ \varepsilon = \int {\frac{1}{2}} \lambda \frac{\sigma }{{\rho {L^2}}}d{t^2} \Rightarrow \lambda \frac{\sigma }{{\rho {L^2}}}{t^3}. $ | (4) |
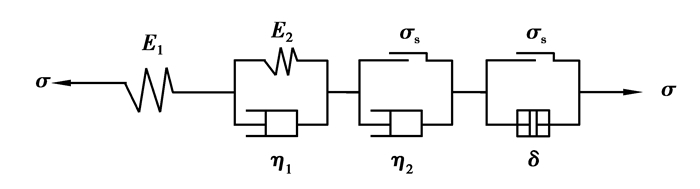
因此,在岩石的第3蠕变阶段,应力、应变及时间关系因遵循公式(4)。故可在西原模型的基础上串联一个绕组δ元件,该元件的特点是在外力情况下应变与时间呈t3关系,以此建立改进西原模型,其力学模型见图 2,并且得出相应的本构方程和蠕变方程。
|
图 2 改进西原体力学模型 Fig. 2 Modified Nishihara Model |
1) 本构方程
| $\begin{array}{l} \left( {A + \frac{1}{E}} \right)\ddot \sigma + \left( {\frac{1}{{{\eta _2}}} - 3A{t^2} + \frac{1}{{{\eta _1}}} + \frac{{{E_2}}}{{{\eta _1}{E_1}}} + A\frac{{{E_2}}}{{{\eta _1}}}} \right)\dot \sigma + \\ \frac{{{E_2}}}{{{\eta _1}}}\frac{{\left( {\sigma - {\sigma _s}} \right)}}{{{\eta _2}}} - \left( {6At + 3A\frac{{{E_2}}}{{{\eta _1}}}{t^2}} \right)\sigma = \ddot \varepsilon + \frac{{{E_2}}}{{{\eta _1}}}\dot \varepsilon A = \frac{\lambda }{{2\rho {L^2}}}, \end{array} $ | (5) |
2) 蠕变方程
当σ < σs时,只有广义开尔文体发生形变。
| $ \varepsilon \frac{{{\sigma _0}}}{{{E_1}}} + \frac{{{\sigma _0}}}{{{E_2}}}\left[ {1 - \exp \left( { - \frac{{{E_2}}}{{{\eta _1}}}t} \right)} \right], $ | (6) |
当σ≥σs时,除了广义开尔文体发生形变外,理想粘塑性体及绕组也将发生形变。
| $ \varepsilon = \frac{{{\sigma _0}}}{{{E_1}}} + \frac{{{\sigma _0}}}{{{E_2}}}\left[ {1 - \exp \left( { - \frac{{{E_2}}}{{{\eta _1}}}t} \right)} \right] + \frac{1}{{{\eta _2}}}\left( {\sigma - {\sigma _s}} \right)t + A\left( {\sigma - {\sigma _s}} \right){t^3}, $ | (7) |
从以上分析可知,改进西原模型从能量角度阐明了岩石蠕变的整个过程。在弹性势能阶段,岩石主要以弹性变形为主,蠕变表现形式为应变速率随时间增加而减小,即减速蠕变阶段;在塑性势能阶段,岩石主要以塑性变形为主,蠕变表现形式为应变速率基本保持不变,是岩石发生变形相对稳定的阶段,即等速蠕变阶段;在动能阶段,岩石主要以复杂变形为主,蠕变表现形式为应变速率迅速增大,岩石在极短的时间内发生破坏,即加速蠕变阶段。
3 模型验证从上述分析可知,理论上改进西原模型用于研究岩石的蠕变特性是恰当的,且在岩石所受荷载小于长期强度时,2种模型研究岩石的蠕变特性所取得的效果是相同的,为此不做冗述。但岩石所受荷载大于长期强度时,2种模型研究岩石的蠕变特性有着明显的区别。
3.1 实验方案采用WDW-200微机控制电子万能实验机(如图 3)对制作好的岩石试件进行蠕变力学实验,分析出不同轴向荷载条件下岩石的应变与时间关系。

|
图 3 WDW-200微机控制电子万能实验机 Fig. 3 WDW-200 universal testing machine |
1) 将岩石试件安放在加载台上,调节横梁,使上承压板与试件上端接触(如图 4);

|
图 4 岩石试件安放图 Fig. 4 Rock sample installation |
2) 以0.03 mm/min的加载速率施加轴向荷载至设定的荷载值;
3) 保持轴向荷载不变,进行岩石蠕变实验,并记录实验过程中岩石试件的轴向应变与时间。
3.3 改进西原模型蠕变力学实验验证 3.3.1 煤岩蠕变实验验证为了验证2种模型研究煤岩蠕变特性的适用性,实验采用山西晋城地区的煤岩进行蠕变力学实验研究。运用matlab软件对实验数据进行拟合,得到各拟合参数(见表 1)及拟合结果(见图 5)。从表 1中可以看出:在相同的荷载条件下,改进西原模型对实际结果的拟合度(R2)要高于西原模型。图 5是2种模型在不同荷载条件下拟合值与实际值的比较。从图中容易发现:1) 煤岩所受荷载由8 MPa增加到12 MPa时,在减速蠕变阶段,煤岩的蠕变速率由0.05%/h增加到0.23%/h;在稳定蠕变阶段,其蠕变速率由0.007%/h增加到0.042%/h;在加速蠕变阶段,其蠕变速率由0.027%/h增加到0.112%/h。2) 随着轴向荷载的增加,煤岩发生蠕变破坏的时间越来越短,轴线荷载为8 MPa时,蠕变时间为58 h;轴向荷载为10 MPa时,蠕变时间为27 h;轴向荷载为12 MPa时,蠕变时间为19 h。3) 随着轴向荷载的增加,减速蠕变阶段和稳定蠕变阶段越来越不明显,而加速蠕变阶段越来越明显。4) 西原模型和改进西原模型所拟合出的曲线都能很好的反映煤岩减速蠕变阶段,而对于稳定蠕变阶段和加速蠕变阶段,改进西原模型拟合效果相对更好。5) 对于加速蠕变阶段,改进西原模型的拟合效果较西原模型具有明显的优越性。
| 表1 岩石蠕变实验拟合参数 Table 1 Fitting parameters of rock creep experiment |

|
图 5 不同轴向荷载煤岩蠕变力学实验实测值与理论值比较 Fig. 5 Comparison between experimental and theoretical values of coal rock creep under different axial loads |
综上分析可知,改进西原模型所拟合的曲线与实测曲线更加吻合,尤其更能准确的反映煤岩的加速蠕变阶段。
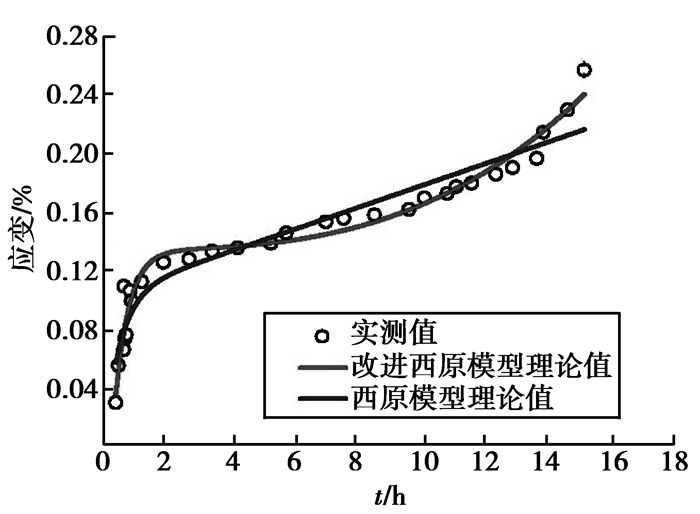
3.3.2 橄榄岩蠕变实验验证本实验岩石试件取自金川集团股份有限公司某矿区的橄榄岩试样。运用matlab软件对该岩石试件蠕变实验结果进行拟合,得到各拟合参数(见表 1)及拟合结果(见图 6)。
|
图 6 38.83 MPa橄榄岩蠕变实验实测值与理论值比较 Fig. 6 Comparison between experiment and theoretical values of peridotite creeping experiment under 38.83 MPa |
从表 1可以看出:在相同荷载条件下,改进西原模型对实测值的拟合程度高于西原模型。图 6直观的反映了2种模型对研究橄榄岩蠕变特性所取得的效果。从图中不难看出:1) 在轴向荷载为38.83 MPa的情况下,橄榄岩减速蠕变阶段所经历的时间为2.1 h;稳定蠕变阶段所经历的时间为12.4 h;加速蠕变阶段所经历的时间为1.7 h。2) 橄榄岩蠕变的3个阶段中,减速蠕变速率0.065%/h;稳定蠕变速率为0.004%/h;加速蠕变速率为0.051%/h。3) 无论是在减速、稳定及加速蠕变阶段,改进西原模型的拟合曲线与实测曲线更加吻合。
结合上述分析可知:改进西原模型能更好研究橄榄岩的蠕变特性。
3.3.3 红砂岩蠕变实验验证本实验岩石试样取自重庆地区的红砂岩,运用matlab软件对实验结果进行拟合,得到了各拟合参数(见表 1)及拟合结果(见图 7)。

|
图 7 50.45 MPa红砂岩蠕变实验实测值与理论值比较 Fig. 7 Comparison between experiment and theoretical values of red standstone creeping experiment under 50.54 MPa |
从表 1可以看出:在相同荷载条件下,改进西原模型对实测值的拟合程度在西原模型的基础上有所提高。
图 7直观反映了2种模型对红砂岩单轴压缩蠕变特性的研究效果,从图中可以看出:1) 在轴向荷载为50.45 MPa时,红砂岩在减速蠕变阶段的蠕变速率为1.78%/h,经历时间为1.1 h;在稳定蠕变阶段,其蠕变速率为0.26%/h,经历时间为0.24 h;在加速蠕变阶段,蠕变速率为1.12%/h,经历时间为0.09 h。2) 在红砂岩蠕变的3个过程中,在减速蠕变阶段,西原模型与改进西原模型对于实测值的拟合效果都比较好,而当蠕变进入到稳定蠕变和加速蠕变阶段后,西原模型对于实测值的拟合效果逐渐变差,且进入加速蠕变阶段后,这种劣势更加突出。
综上所述,改进西原模型能更好地表现红砂岩的蠕变特性,特别是能够恰当的反映出加速蠕变阶段的特性。
3.3.4 盐膏岩蠕变实验验证本次实验的岩芯取自新疆塔里木盆地的盐膏岩地层,通过单轴压缩蠕变力学实验,确定出该区域的盐膏岩长期强度为20.0~21.5 MPa。
运用Matlab软件对实验结果进行参数拟合,得到拟合参数(见表 1及拟合结果(见图 8))。
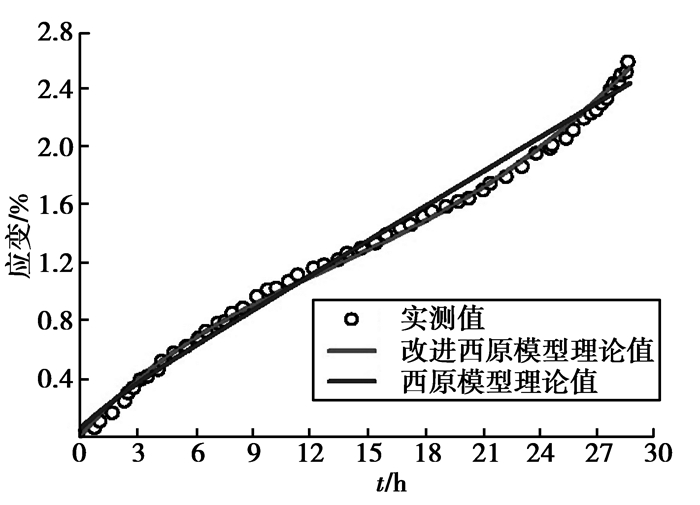
|
图 8 21.5盐膏岩蠕变实验实测值与理论值比较 Fig. 8 Comparison between experiment and theoretical values of salt-gypsum rock creeping experiment under 21.5 MPa |
从表 1可以看出:在轴向荷载相同的情况下,改进西原模型对实测值的拟合程度高于西原模型。从图 8中可以看出:1) 盐膏岩在轴向荷载条件下,应变—时间基本呈线性关系,蠕变过程中3个阶段的过渡不明显,在经历28 h,应变达到2.76%后,盐膏岩发生蠕变破坏。2) 改进西原模型对整个蠕变过程的拟合程度较西原模型好。
综上所述:改进西原模型所研究的盐膏岩蠕变曲线与实际的蠕变曲线吻合程度较高,对加速蠕变阶段曲线也有很好的反映。而西原模型对于加速蠕变阶段曲线的反映不明显。
4 结 论通过以上对改进西原模型的理论分析及实验验证,得出了以下结论:
1) 在油气井工程中,从能量角度出发,运用外力功与岩石内部能量的转换关系来研究岩石的蠕变特性,并且建立相应的蠕变模型是可行的。
2) 在岩石所受荷载大于长期强度的情况下,建立的改进西原模型对煤岩、橄榄岩、红砂岩和盐膏岩4种岩石的蠕变特性具有明显的优越性。
3) 改进西原模型较原西元模型能够更好地研究岩石的加速蠕变阶段。从能量角度分析是因为该阶段岩石内部储存能量的能力已经达到极限,外力功主要转换为动能,故表现出加速蠕变的特征。
研究主要从能量的角度研究了煤岩、橄榄岩、红砂岩、盐膏岩4种岩石的蠕变特性,揭示了它们在蠕变过程中的能量转换关系,并且通过蠕变力学实验验证表明:改进西元模型适于研究上述岩石的蠕变规律,而对于其他岩石是否适用需要进一步的考证。
| [1] | 尹光志,何兵,王浩,等.深部采动影响下覆岩蠕变损伤破坏规律[J].煤炭学报, 2015,40(6):1390-1395. YIN Guangzhi, HE Bing, WANG Hao, et al. Damage law of overlying rock induced by mining[J]. Journal of China Coal Society, 2015, 40(6):1390-1395. (in Chinese)( 1) 1) |
| [2] | 范翔宇.复杂钻井地质环境描述[M].北京:石油工业出版,2012. FAN Xiangyu. Complex drilling geological environment description[M]. Beijing:China Petroleum Industry Press, 2012.(in Chinese)( 1) 1) |
| [3] | Falaleev G N. Rock creep degree assessment[J]. Journal of Mining Science, 2010, 46(1):34-37.( 1) 1) |
| [4] | 何峰,王来贵,王振伟,等.煤岩蠕变-渗流耦合规律实验研究[J]. 煤炭学报, 2011, 36(6):930-933. HE Feng, WANG Laigui, WANG Zhenwei, et al. Experimental study on creep-seepage coupling law of coal(rock)[J]. Journal of China Coal Society, 2011, 36(6):930-933. (in Chinese)( 1) 1) |
| [5] | Zhu Y B, Yu H M. Unsaturated creep behaviors of weak intercalated soils in soft rock of badong formation[J]. Journal of Mountain Science, 2015, 12(6):1460-1470.( 1) 1) |
| [6] | Xu W Y, Wang R B, Wang W, et al. Creep properties and permeability evolution in triaxial rheological tests of hard rock in dam foundation[J]. Journal of Central South University, 2012, 19(1):252-261.( 1) 1) |
| [7] | 徐鹏,杨圣奇.循环加卸载下煤的黏弹塑性蠕变本构关系研究[J].岩石力学与工程学报,2015,34(3):537-545. XU Peng, YANG Shengqi. Study of visco-elasto-plastic constitutive model of coal under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(3):537-545. (in Chinese)( 1) 1) |
| [8] | Yang Y, Lai Y, Chang X. Experimental and theoretical studies on the creep behavior of warm ice-rich frozen sand[J]. Cold Regions Science and Technology, 2010, 63(1-2):61-67.( 1) 1) |
| [9] | 范翔宇,张千贵,艾巍,等.煤岩储气层岩石蠕变特性与本构模型研究[J].岩石力学与工程学报,2013(S2):3732-3739. FAN Xiangyu, ZHANG Qiangui, AI Wei, et al. Research on cereep property and constitutive model of coal in coal bed gas reservoir[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, (S2):3732-3739. (in Chinese)( 1) 1) |
| [10] | 杨逾,李盈,周小科.基于西原加速模型的煤岩蠕变试验研究[J].煤炭学报,2014,39(11):2190-2194. YANG Yu, LI Ying, ZHOU Xiaoke. Study on the coal creep test based on the improved Nishihara model[J]. Journal of China Coal Society, 2014, 39(11):2190-2194. (in Chinese)( 1) 1) |
| [11] | Kang J H, Zhou F B, Liu C, et al. A fractional nonlinear creep model for coal considering damage effect and experimental validation[J]. International Journal of Non-Linear Mechanics, 2015, 76:20-28.( 1) 1) |
| [12] | 李金和,陈文玲,王洪旭.大理岩单轴蠕变模型参数[J].世界地质,2014,33(2):488-493. LI Jinhe, CHEN Wenling, WANG Hongxu. Uniaxial creep modal parameters of marble[J]. Global Geology, 2014, 33(2):488-493. (in Chinese)( 1) 1) |
| [13] | 陈绍杰,郭惟嘉,程国强,等.深部条带煤柱蠕变支撑效应研究[J].采矿与安全工程学报,2012,29(1):48-53. CHEN Shaojie, GUO Weijia, CHENG Guoqiang, et al. Research on creep supporting effect of deep strip pillar[J]. Journal of Mining and Safety Engineering, 2012, 29(1):48-53. (in Chinese)( 1) 1) |
| [14] | 周长冰,万志军,张源,等.高温三轴应力下气煤蠕变特征及本构模型[J].煤炭学报,2012,37(12):2020-2025. ZHOU Changbing, WAN Zhijun, ZHANG Yuan, et al. Creep characteristics and constitutive model of gas coal mass under high temperature and triaxial stress[J]. Journal of China Coal Society, 2012, 37(12):2020-2025. (in Chinese)( 1) 1) |
| [15] | 赵斌,王芝银,伍锦鹏.煤岩不同应力水平的蠕变及破坏特性[J].中国石油大学学报:自然科学版,2013,37(4):140-144. ZHAO Bin, WANG Zhiyin, WU Jinpeng. Creep and damage characteristics of coal rock under different stresses[J].Journal of China University of Petroleum:Edition of Natural Science, 2013, 37(4):140-144. (in Chinese)( 1) 1) |
| [16] | 刘钦,李术才,李利平,等.软弱破碎围岩隧道炭质页岩蠕变特性试验研究[J].岩土力学,2012(S2):21-28. LIU Qin, LI Shucai, LI Liping, et al. Experimental study of carbonaceous shale creep characters of weak broken surrounding rock tunnel[J]. Rock and Soil Mechanics, 2012, (S2):21-28. (in Chinese)( 1) 1) |
| [17] | 杨红伟,许江,彭守建,等.孔隙水压力分级加载砂岩蠕变特性研究[J].岩土力学,2015(S2):365-370. YANG Hongwei, XU Jiang, PENG Shoujian, et al. Study of sandstone creep characteristics under stepwise loading pore water pressures[J]. Rock and Soil Mechanics, 2015, (S2):365-370. (in Chinese)( 1) 1) |
| [18] | Gao Y, Gao F, Zhang Z Z, et al. visco-elastic-plastic model of deep underground rock affected by temperature and humidity[J]. Mining Science & Technology, 2010, 20(2):183-187.( 1) 1) |
| [19] | Zhou H W, Wang C P, Han B B, et al. A creep constitutive model for salt rock based on fractional derivatives[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(1):116-121.( 1) 1) |
| [20] | Cristescu N D. A general constitutive equation for transient and stationary creep of rock salt[J]. International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts, 1993, 30(2):125-140.( 1) 1) |
| [21] | 张新民,庄军,张遂安.中国煤层气地质与资源评价[M].北京:科学出版社,2002:12-30. ZHANG Xinmin, ZHUANG Jun, ZHANG Suian. The geological and resources evaluation of coal bed gas in China[M]. Beijing:Science Press, 2002:12-30.(in Chinese)( 1) 1) |
| [22] | 彭瑞东,谢和平,周宏伟.岩石变形破坏过程的热力学分析[J].金属矿山,2008(3):61-64+132. PENG Ruidong, XIE Heping, ZHOU Hongwei. Therm odynamic analysis of rock deformation and failure process[J]. Metal Mine, 2008(3):61-64.(in Chinese)( 2) 2) |
| [23] | 蔡美峰,何满潮,刘东燕.岩石力学与工程[M].北京:科学出版社,2002:199-200. CAI Meifeng, HE Manchao, Liu Dongyan. Rock mechanics and engineering[M]. Beijing:Science Press, 2002:199-200.(in Chinese)( 1) 1) |
 2016, Vol. 39
2016, Vol. 39


