2. 重庆大学汽车工程学院, 重庆 400044
2. College of Automotive Engineering, Chongqing University, Chongqing 400044, P. R. China
在汽车悬架中既是弹性元件又是导向机构的钢板弹簧的刚度特性是极其重要的设计参数,直接影响汽车整车的性能,准确设计和计算钢板弹簧的刚度特性非常重要。“共同曲率法”和“集中载荷法”是钢板弹簧刚度特性分析的传统计算方法[1],在工程中已普遍使用。随着计算机技术的发展,“有限元法”和“离散梁法”[2-3]等建立钢板弹簧模型的方法成为主流方法。“有限元法”按照板簧各片的结构尺寸和材料性质进行建模仿真[4-6],无需进行过多简化。“离散梁法”依据Timoshenko理论[7]将钢板弹簧各个叶片离散成若干个小块,块与块之间由无质量的柔性离散梁连接[8],各小块视为刚体。因为这两种方法均能较准确地模拟出钢板弹簧作用过程中的实际物理情形,得到更精确的刚度特性,近年来受到广泛关注。文献[9]以某车型底盘开发项目为例对钢板弹簧的“有限元法”模型和“离散梁法”模型进行了建模分析;文献[10]以某型重型货车的悬架开发项目为例对钢板弹簧“离散梁法”模型进行了分析。这些文献对钢板弹簧建模的各种方法进行了深入的研究,但是对钢板弹簧建模方法之间的对比研究较少。
笔者以某MPV整车开发项目中某渐变刚度钢板弹簧为例,通过“共同曲率法”、“集中载荷法”、“有限元法”和“离散梁法”4种方法分别计算得到钢板弹簧的刚度特性。将其与试验值进行比较,结果表明,在针对该钢板弹簧的刚度分析中,“离散梁法”得到的刚度特性更接近试验值。
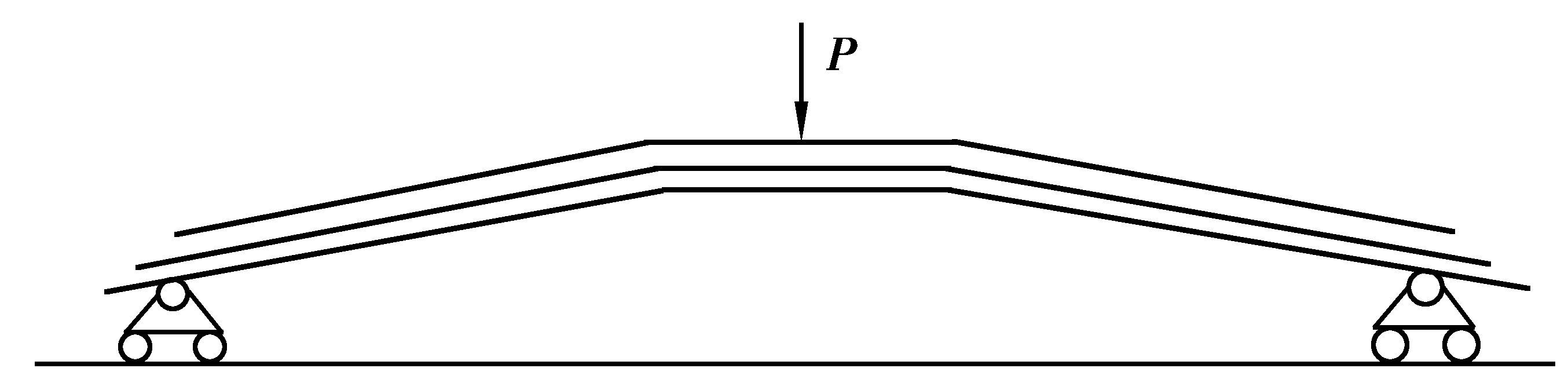
1、 钢板弹簧刚度试验国家标准国标GB/T 19844—2005《钢板弹簧》[11]中对钢板弹簧刚度试验进行了规定。刚度试验简图如图 1所示,带卷耳的钢板弹簧夹持方法如图 2所示。
|
图 1 钢板弹簧刚度试验简图 Figure 1 Leaf spring stiffness test |

|
图 2 钢板弹簧夹持方法简图 Figure 2 Leaf spring fixed method |
某型MPV后悬架主、副簧分配的渐变刚度钢板弹簧材料为55SiMnVB,其物理参数如表 1,板簧结构参数如表 2。由于该板簧前后对称[12],取其一半建立有限元模型进行分析。因为钢板弹簧结构特点为长度和宽度方向上的尺寸远大于其厚度的尺寸,故钢板弹簧是典型的薄板构件。因此采用抽取中面、划分面单元的形式来划分网格。
| 表 1 钢板弹簧材料参数 Table 1 Material parameters of leaf spring |
| 表 2 钢板弹簧结构参数 Table 2 Structural parameters of leaf spring |
在相邻的钢板弹簧叶片之间设置接触对,以模拟实际接触行为[13-14]。共设置4个接触对,每一个接触对均有主面和从面,如图 3所示。

|
图 3 钢板弹簧接触设置简图 Figure 3 Contact setting of leaf spring |
在半钢板弹簧模型对称面节点上施加固定约束,在卷耳处施加集中载荷,以模拟实际工作情况。建立有限元模型,共有20 424个面单元、21 394个节点,如图 4所示。

|
图 4 钢板弹簧有限元模型 Figure 4 FEM model of leaf spring |
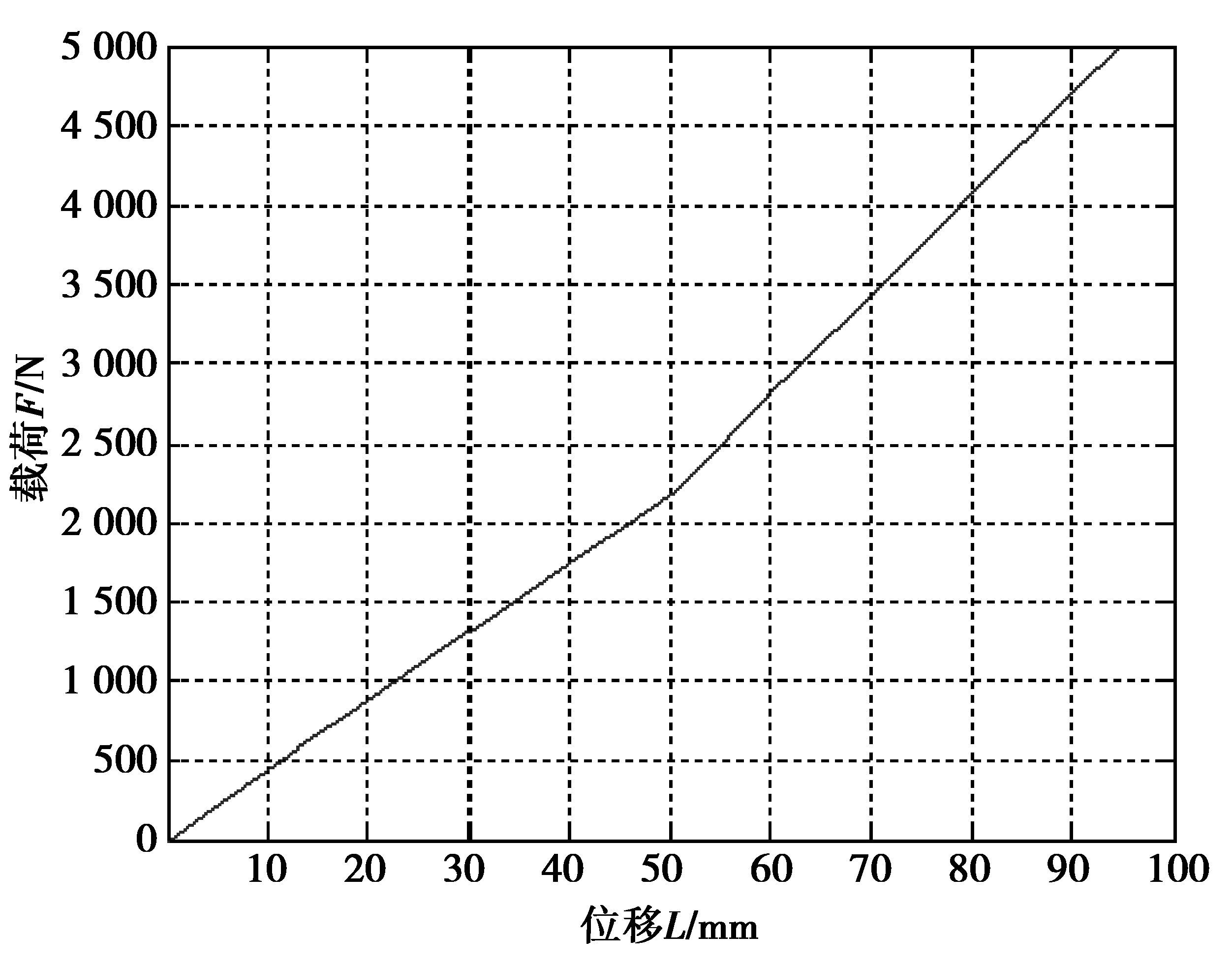
将整个载荷分解为20个子载荷步加载(至满载的1.5倍)在有限元模型上,调用Optistruct求解器进行求解。处理每个子载荷步的载荷和位移即可得到该钢板弹簧的载荷位移曲线,即钢板弹簧的刚度特性结果如图 5、图 6所示。
|
图 5 钢板弹簧载荷位移曲线 Figure 5 Load-displacement curve of leaf spring |

|
图 6 钢板弹簧刚度位移曲线 Figure 6 Stiffness-displacement curve of leaf spring |
通过“有限元法”计算得到该主、副簧分配的渐变刚度钢板弹簧的刚度:主簧刚度为43.45 N/mm,复合刚度为63.42 N/mm。
(2.2) 钢板弹簧的离散梁模型钢板弹簧离散梁模型依据Timoshenko理论[7]将钢板弹簧各个叶片离散成若干个小块,各小块视为一个刚体。为了减少钢板弹簧离散梁模型的自由度,利用钢板弹簧等效中性面原理将主、副簧分配的渐变刚度钢板弹簧等效为两个叶片[15],各叶片由以硬点为基础的小块组成。各硬点处等效厚度h,由下列公式得到:
| h=3√h31+h32+h33, |
式中:h1、h2、h3分别指钢板弹簧第1片、第2片和第3片在某硬点处的厚度。若第i片在接触范围外,则对应的hi=0;钢板弹簧的第4片与第5片简化为副簧的过程同理。
简化后钢板弹簧主簧、副簧各硬点相对坐标及等效厚度分别如表 3、表 4所示。
| 表 3 主簧各硬点处坐标及厚度 Table 3 Coordinates and thickness of hard point on main spring |
| 表 4 副簧各硬点处坐标及厚度 Table 4 Coordinates and thickness of hard point on auxiliary spring |
钢板弹簧前、后卷耳坐标和后吊耳车架连接点的整车坐标,如表 5所示。
| 表 5 连接点坐标 Table 5 Coordinates of join points |
在Adams/Chassis模块钢板弹簧编译器中进行离散化计算。最终在Adams/Car中得到了钢板弹簧模型,如图 7所示。

|
图 7 钢板弹簧离散梁模型简图 Figure 7 Beam element model of leaf spring |
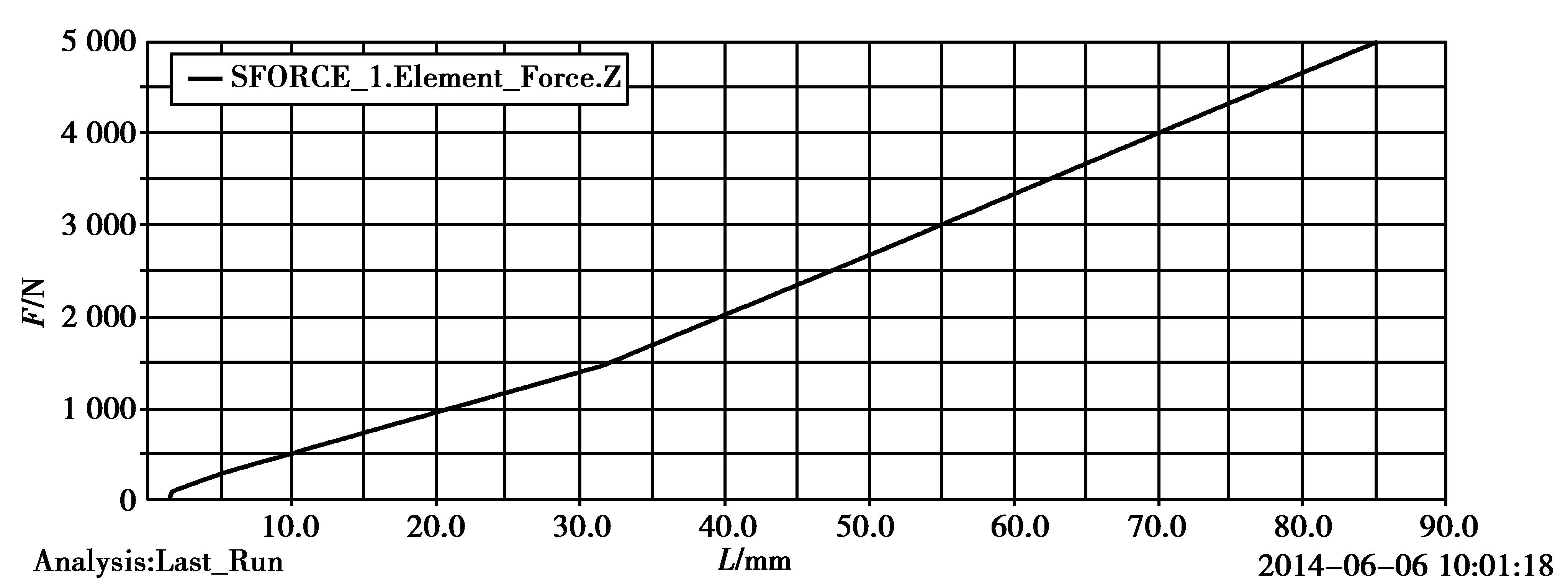
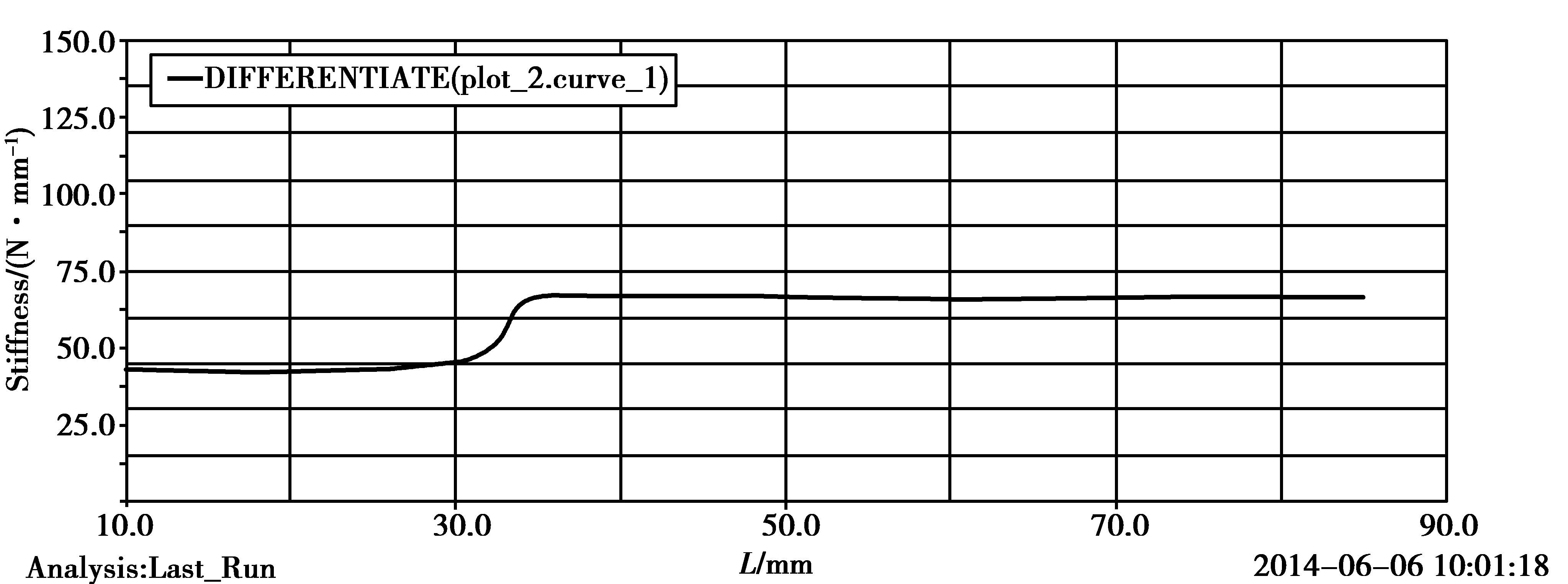
按照国标对离散梁模型进行刚度分析,加载[16]得到载荷位移曲线与刚度位移曲线,如图 8~9所示。
|
图 8 钢板弹簧载荷位移曲线 Figure 8 Load-displacement curve of leaf spring |
|
图 9 钢板弹簧刚度位移曲线 Figure 9 Stiffness-displacement curve of leaf spring |
通过“离散梁法”计算得到该主、副簧分配的渐变刚度钢板弹簧的刚度:主簧刚度为43.83 N/mm,复合刚度为65.92 N/mm。
(2.3) 钢板弹簧的有限元简化模型由于在钢板弹簧离散梁模型建模过程中利用了中性面原理对模型进行了简化,考虑到模型简化会对结果造成影响,故将有限元模型依据中性面原理进行简化,计算结果进行对比。建立起钢板弹簧有限元简化模型,共有9 632个面单元,10 078个节点,如图 10所示。

|
图 10 钢板弹簧有限元模型 Figure 10 Simplified FEM model of leaf spring |
通过“有限元法”计算得到该主、副簧分配的渐变刚度钢板弹簧的刚度:主簧刚度为43.10 N/mm,复合刚度为62.62 N/mm。
3、 结果分析从厂商处获得某MPV底盘中渐变刚度钢板弹簧的刚度试验值,将“共同曲率法”、“集中载荷法”、“有限元法”、“有限元简化法”和“离散梁法”得到的刚度特性与该钢板弹簧的刚度试验值进行比较,如表 6所示。从表中可知,“共同曲率法”计算的主簧刚度与试验值的误差最大,达到了11.17%,计算的复合刚度误差小于“集中载荷法”,但大于“有限元法”和“离散梁法”;“集中载荷法”计算的复合刚度误差最大,达12.14%,远大于其他方法,主簧刚度误差也达7.59%,大于“有限元法”和“离散梁法”。“离散梁法”的主簧刚度和复合刚度均最接近试验值;“有限元法”与试验值的差异介于传统方法计算结果和“离散梁法”计算结果之间;“有限元简化法”的计算结果的误差大于“有限元法”。
| 表 6 钢板弹簧刚度值比较 Table 6 Comparison of stiffness of leaf spring |
作为钢板弹簧刚度分析传统计算方法的“共同曲率法”和“集中载荷法”在计算中用悬臂梁来模拟,这与实际工作中钢板弹簧受力发生大变形有较大差异,且钢板弹簧各叶片之间的接触方式模拟较粗糙,这是造成结果与试验值有较大误差的原因;“有限元法”模型已知钢板弹簧的材料特性,能模拟钢板弹簧各叶片之间的接触作用,模型较为准确,但模型中板簧各叶片之间的接触状态和摩擦因数会对刚度特性产生影响;“离散梁法”模型的精度与所建模型中板簧的片数和每片所分的小块数量有关,板簧片数越多、小块数越多则精度越高,但随之自由度与模型复杂度也会越高。
4、 结 论依据钢板弹簧国家标准GB/T 19844—2005,针对某型渐变刚度钢板弹簧建立了有限元模型和离散梁模型,并分别进行了仿真,得到其刚度特性。将仿真结果和传统计算方法的结果一起与试验值进行了比较,分析讨论了产生差异的原因。结果表明,在该钢板弹簧刚度分析中运用离散梁模型得到的刚度特性更加接近试验值。本研究中,为了减少离散梁模型的自由度,利用钢板弹簧中性面原理,将主、副簧分配的渐变刚度钢板弹簧等效为两个叶片。今后将考虑建立更加接近原钢板弹簧的模型进行分析。
| [1] |
于安和, 桂良进, 范子杰.
钢板弹簧刚度特性的有限元分析[J]. 汽车技术 , 2007 (2) : 26–29.
YU Anhe, GUI Liangjin, FAN Zijie.
Finite element analysis on the stiffness of leaf springs[J]. Automotive Technology , 2007 (2) : 26–29.
( 1) 1)
|
| [2] |
古玉峰, 吕彭民, 单增海.
汽车钢板弹簧多体动力学建模综述[J]. 汽车工程 , 2014, 36 (12) : 1513–1519.
GU Yufeng, LV Pengmin, SHAN Zenghai.
A review on multi-body dynamics modeling for vehicle leaf springs[J]. Automotive Technology , 2014, 36 (12) : 1513–1519.
( 1) 1)
|
| [3] |
李凌阳, 张云清, 覃刚, 等.
钢板弹簧建模方法研究[J]. 汽车工程 , 2013, 35 (7) : 660–666.
LI Lingyang, ZHANG Yunqing, QIN Gang, et al.
A research on the modeling methods of leafspring[J]. Automotive Technology , 2013, 35 (7) : 660–666.
( 1) 1)
|
| [4] |
Omar M A.Finite element modeling of leaf springs for vehicle system applications[D].Chicago:University of Illinoisat Chicago,2003.
( 1) 1)
|
| [5] | Li Q, Li W. A contact finite element algorithm for the multileaf spring of vehicle suspension systems[J]. Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering , 2004, 218 (3) : 305–314. DOI:10.1243/095440704322955821 |
| [6] |
Kirby D,Charniga R.A finite element and experimental analysis of a light truck leaf spring system subjected to pre-tension and twist loads[C]//2005 SAE Commercial Vehicle Engineering Conference,November 1-3,2005,Chicago,Illinois.[S.l.]:SAE Technical Paper,2005:1984-1996.
( 1) 1)
|
| [7] |
Prasade U,Medepalli S,Moore D,et al.Beam element leaf spring suspension model development and assessment using road load data[C]//SAE 2006 World Congress & Exhibition,April 3-6,2006,Detroit,Michigan.[S.l.]:SAE Technical Paper,2006:1-7.
( 2) 2)
|
| [8] |
Sugiyama H, Shabana A A, Omar M A, et al.
Development of Nonlinear Elastic Leaf Spring Model for MultibodyVehicle Systems[J]. Computer Methods in Applied Mechanics and Engineering , 2006, 195 (50/51) : 6925–6941.
( 1) 1)
|
| [9] |
李刚.渐变刚度钢板弹簧后悬架有限元与动力学建模及仿真[D].长春:吉林大学,2011.
LI Gang.Finite element and dynamics modeling and simulation of gradual stiffness leaf spring rear suspension[D].Changchun:Jilin University,2011.(in Chinese)
( 1) 1)
|
| [10] |
史世俊.ADAMS钢板弹簧离散梁建模及重型载货汽车悬架K & C特性仿真[D].长春:吉林大学,2012.
SHI shijun.Discrete beam modeling of the leaf spring in ADAMS and simulation of suspension K & G characteristics for heavy-duty truck[D].Changchun:Jilin University,2012.(in Chinese)
http://cdmd.cnki.com.cn/article/cdmd-10183-1012368097.htm ( 1) 1)
|
| [11] |
中国人民共和国国家质量监督检验检疫总局,中国国家标准化委员会.GB/T 19844-2005钢板弹簧[S].北京:中国标准出版社,2005.
The State Administration of Quality Supervision,Inspection and Quarantine of the People's Republic of China,China national standardization committee.GB/T 19844-2005 steel plate spring[S].Beijing:China Standard Press,2005.(in Chinese)
( 1) 1)
|
| [12] |
胡玉梅, 邓兆祥, 王欣, 等.
汽车后悬架的非线性有限元分析[J]. 重庆大学学报(自然科学版) , 2003, 26 (4) : 38–41.
HU Yumei, DENG Zhaoxiang, WANG Xin, et al.
Analysis of leaf suspension of vehicle using non-linear finite element[J]. Journal of Chongqing University:Natural Science Edition , 2003, 26 (4) : 38–41.
( 1) 1)
|
| [13] |
席敏, 刘桂萍, 雷飞, 等.
考虑片间接触的汽车钢板弹簧动力学建模[J]. 汽车工程 , 2012, 34 (8) : 751–755.
XI Min, LIU Guiping, LEI Fei, et al.
Dynamics modeling of vehicle leaf spring with consideration of inter-leaf contact[J]. Automotive Engineering , 2012, 34 (8) : 751–755.
( 1) 1)
|
| [14] |
廖林清, 李常鑫, 苏道奇, 等.
少片变截面式钢板弹簧的刚度研究[J]. 重庆理工大学学报(自然科学版) , 2013, 27 (5) : 6–10.
LIAO Linqing, LI Changxin, SU Daoqi, et al.
Research for the Stiffness of the Taper Leaf Springs[J]. Journal of Chongqing University of Technology:Natural Science , 2013, 27 (5) : 6–10.
( 1) 1)
|
| [15] |
鞠成超, 韩旭, 刘桂平.
钢板弹簧离散梁动力学参数反求[J]. 汽车工程 , 2009, 31 (9) : 860–863.
JU Chengchao, HAN Xu, LIU Guiping.
Reverse solution for discrete beam dynamics parameters of leaf spring[J]. Automotive Technology , 2009, 31 (9) : 860–863.
( 1) 1)
|
| [16] |
李杰, 张喆, 朱毅杰, 等.
平衡悬架钢板弹簧模型的建立与仿真[J]. 重庆大学学报 , 2011, 34 (6) : 31–35.
LI Jie, ZHANG Zhe, ZHU Yijie.
Modeling and simulation of leaf spring for tandem suspension[J]. Journal of chongqing university , 2011, 34 (6) : 31–35.
( 1) 1)
|
 2016, Vol. 39
2016, Vol. 39


