风能作为一种清洁、可再生新型能源在国民经济中扮演着愈发重要的角色。风电增速齿轮箱作为风电的核心设备,常年受极端温差和复杂载荷的影响,其振动特性和可靠性一直是研究人员关注的重点[1]。因此,开展风电增速齿轮箱动力学性能优化方法的研究具有重要的实用价值。
国内外学者已对齿轮系统动力学性能进行了大量的研究工作。采用有限元方法建立了包含齿轮副、传动轴、轴承和箱体的齿轮系统动力有限元模型,并对齿轮系统进行动力学仿真分析及试验研究[2-4];采用集中参数法建立了内外载荷作用下系统的动力学方程,求得齿轮传动系统的动态响应[5-9]。在齿轮系统动力学性能优化研究方面,Bozca[10]以齿轮几何参数为优化设计变量,对箱体的振动噪声进行优化;Faggioni等[11]开展了齿廓修形及传动误差对齿轮箱振动的影响研究;张庆伟等[12]采用混合离散变量组合法对风电齿轮箱振动加速度和齿轮系统质量进行了优化求解;秦大同等[13]建立了增速齿轮箱传动系统扭转振动模型,用谐波平衡法求得目标函数表达式,建立以行星轮扭转振动加速度幅值最小和传动系统总质量最轻为目标的优化设计数学模型,采用Matlab进行了优化求解;Kim等[14]提出了利用等效静态载荷将非线性优化问题转化为线性静态优化问题的求解方法。魏静等[15]建立齿轮系统耦合非线性动力学模型,计算了内外部载荷作用下风电齿轮箱的动态响应。但是,目前针对复杂的齿轮结构系统开展动力学性能优化及优化效果评价的研究报道相对较少。
笔者以风电增速齿轮箱为例,借助ANSYS软件建立参数化动力有限元模型,并计算齿轮系统的动态响应。在此基础上,利用零阶和一阶优化相结合的算法,对齿轮系统进行动力学性能优化,并评价其优化效果。
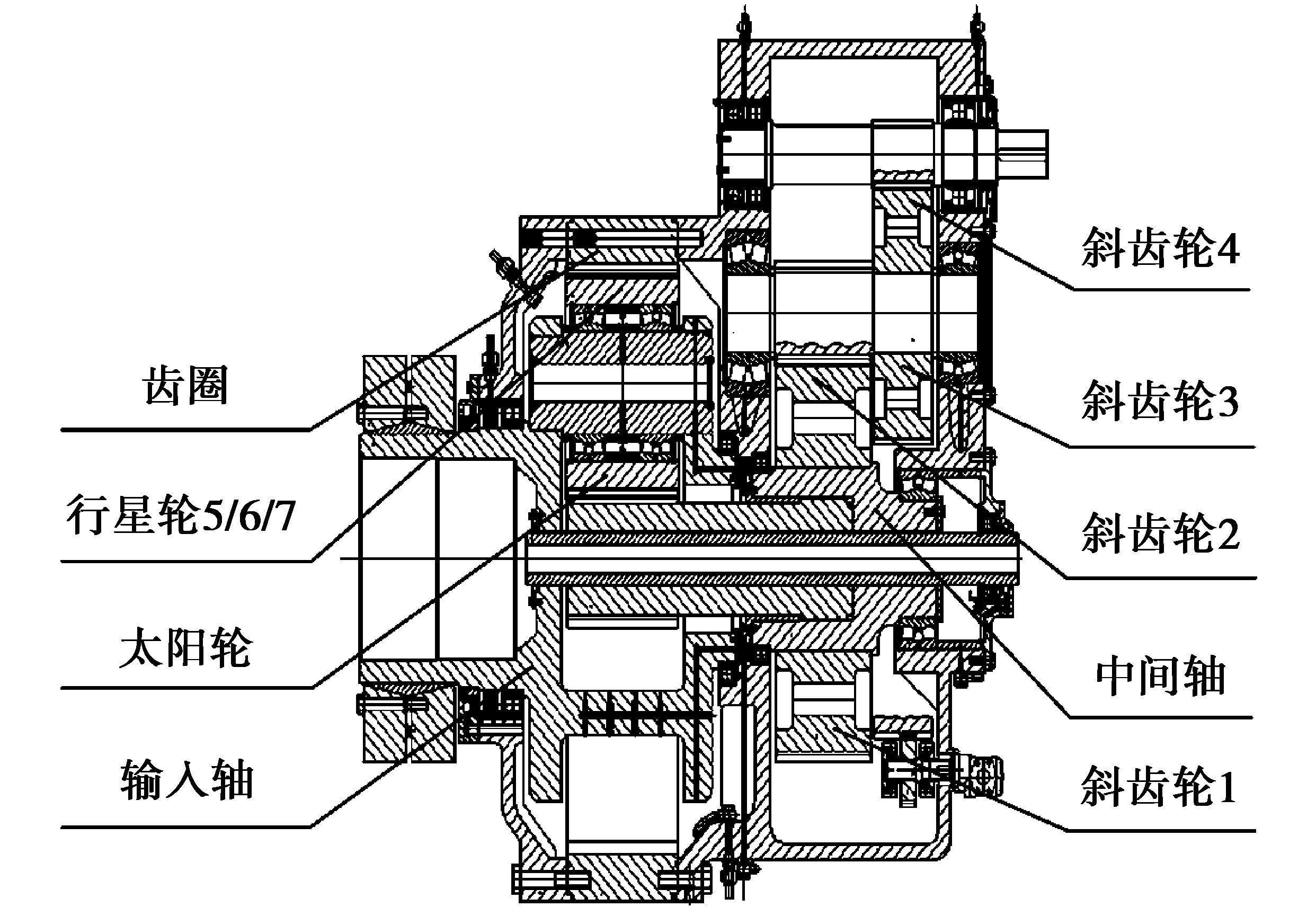
1、 增速齿轮箱动力学性能分析风电增速齿轮箱的传动系统如图 1所示,由一级行星轮传动和两级平行轴斜齿轮传动组成。
|
图 1 风电增速齿轮箱传动系统 Figure 1 The transmission system of wind power speed-increase gearbox |
增速齿轮箱的输入功率、输入转速以及各级齿轮副的齿数、模数如表 1所示。
| 表 1 增速齿轮箱运行工况及齿轮副参数 Table 1 The operating conditions and gearparameters of speed-increase gearbox |
在ANSYS中建立增速齿轮箱参数化实体模型及有限元模型,如图 2所示,图中坐标轴X、Y、Z分别表示横向、竖向和轴向。用弹簧单元模拟轴承的支承和轮齿的啮合,在齿轮箱支座部位和输入轴左端轴承处施加固定约束。

|
图 2 增速齿轮箱的有限元网格 Figure 2 The finite element mesh of speed-increase gearbox |
用Lanczos法对齿轮箱系统进行模态分析,得到系统前8阶固有频率和固有振型,如表 2所示。
| 表 2 齿轮系统前8阶固有频率及主要振型 Table 2 The first 8-order natural frequency and modes of gear system |
风电增速齿轮箱行星齿轮级、第1、2级斜齿轮副的啮合频率分别为35.7、133.1、623.3 Hz。表 1中前7阶频率均避开了齿轮系统的啮合频率及其倍频,第8阶频率虽然与行星齿轮级啮合频率的3倍频接近,但振型不同,故箱体不会发生共振。
(1.2) 动态响应分析各级齿轮副的内部激励计算式为
| $F\left( t \right)=\Delta k\left( t \right)\cdot e\left( t \right)+S\left( t \right),$ | (1) |
式中:F(t)为内部载荷激励;Δk(t)为时变啮合刚度;e(t)为齿面综合误差;S(t)为冲击激励。
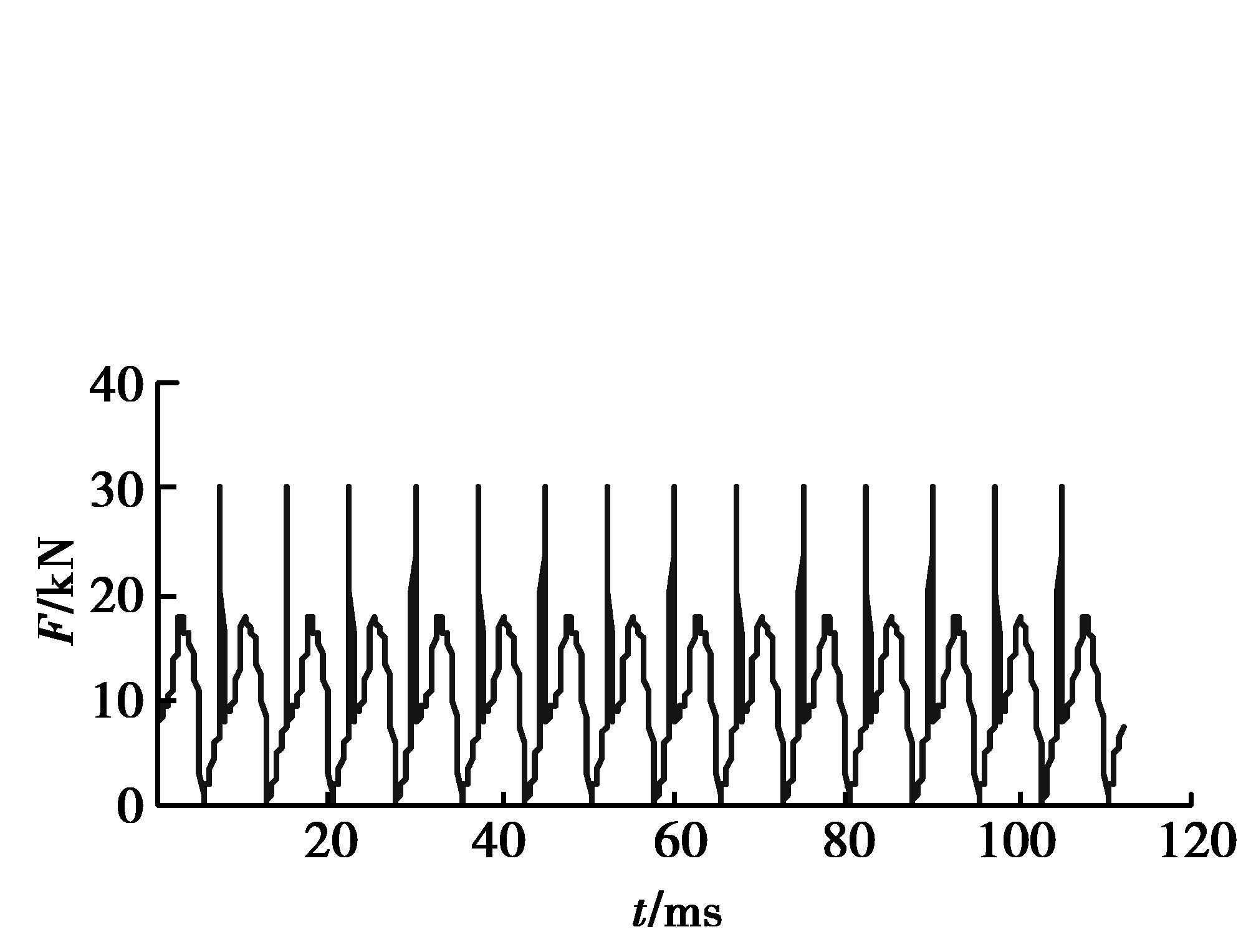
图 3给出了第1级斜齿轮副的内部激励。将各级齿轮副的内部激励以命令流的形式施加在齿轮副啮合线上,采用直接积分法计算齿轮箱动态响应。
|
图 3 第1级斜齿轮副内部激励 Figure 3 The internal excitation of the first grade helical gear pair |
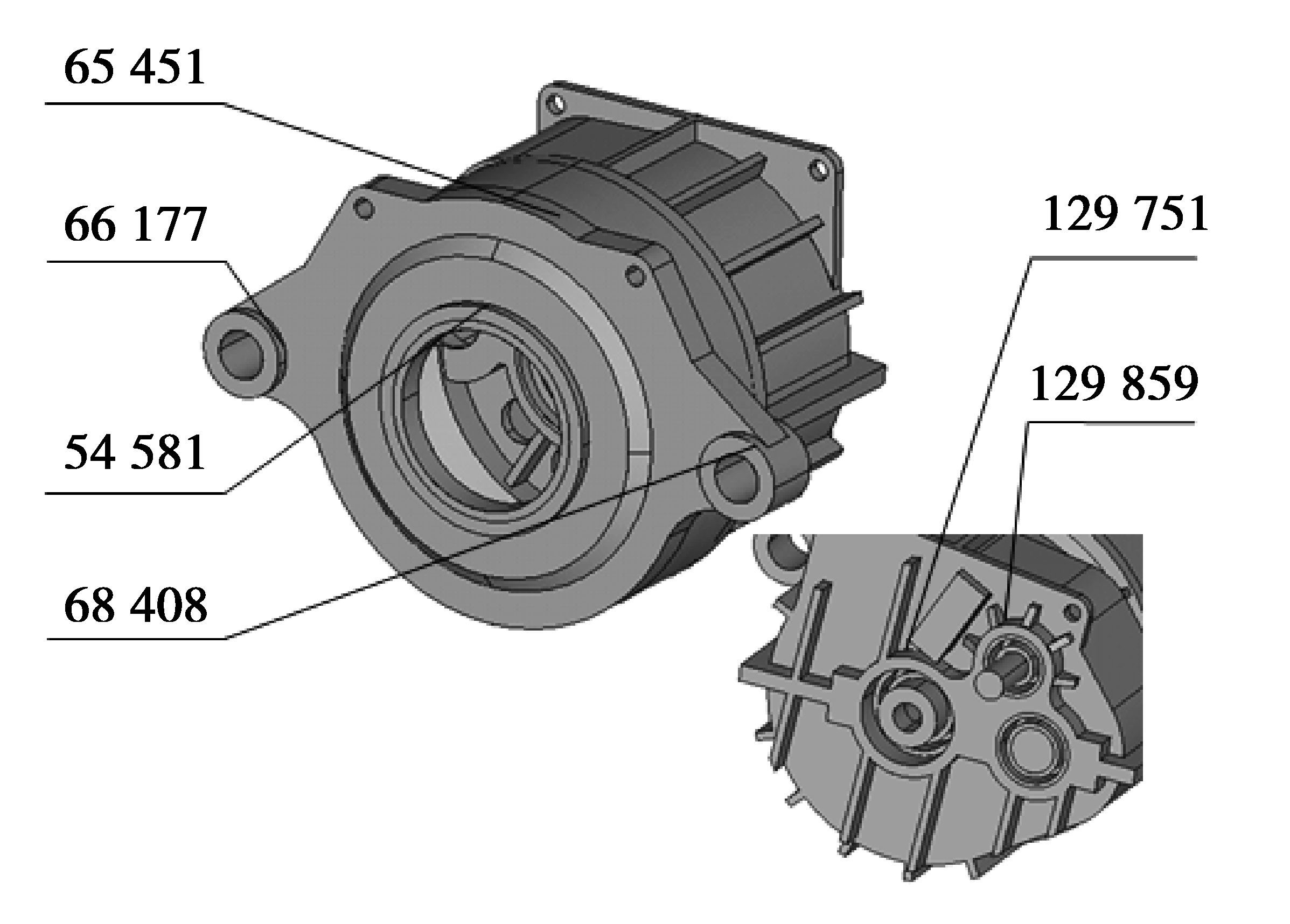
求解中,设置求解步长Δt=0.267 4 ms,求解时间t=112 ms,选取如图 4所示的箱体上顶部、支座和轴承座顶部共6个位置为响应评价点。表 3~5给出了箱体表面评价点的动态响应。
|
图 4 增速齿轮箱动态响应评价点 Figure 4 The dynamic response evaluation point of speed-increase gearbox |
| 表 3 箱体表面节点振动位移均方根值(μm) Table 3 The vibration displacement RMS of nodes on gearbox(μm) |
| 表 4 箱体表面节点振动速度均方根值(m/s) Table 4 The vibration velocity RMS of nodes on gearbox(m/s) |
| 表 5 箱体表面节点振动加速度均方根值(m/s) Table 5 The vibration acceleration RMS of nodes on gearbox(m/s) |
由表可知,节点66 177和68 408的振动较小,这是因为所选节点靠近固定约束面;节点129 751的振动较大,尤其是轴向加速度,原因是第1级斜齿轮副的轴向动载荷较大。动态响应分析结果可为响应优化的设计参数选择提供依据,选择振动较大的位置作为优化的评价点通常可显著减小齿轮箱的总体振动水平。
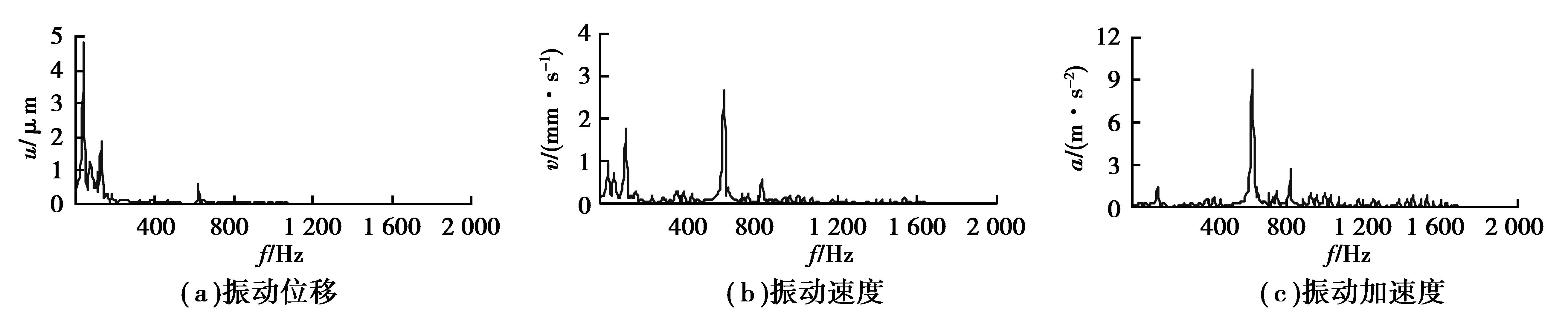
图 5给出了节点129 571 Y向的振动位移、振动速度和振动加速度的频域曲线。由图可知,齿轮箱的频域振动响应峰值出现在齿轮副的啮合频率及其倍频附近
|
图 5 节点129 751 Y向振动响应频域曲线 Figure 5 The frequency domain curve of Y direction vibration response of node 129 751 |
图 6给出了齿轮箱动态响应优化的流程图。动态响应优化设计时,首先选择零阶优化方法,采用最小二乘逼进,在求解域中初步求得最优设计变量;然后选择一阶优化方法,采用梯度寻优,更精确地确定最优解。

|
图 6 齿轮箱动态响应优化流程 Figure 6 The process of dynamic response optimization of gearbox |
动态响应优化主要目的是减小齿轮箱的振动。以箱体表面评价点1~6的振动加速度均方根最小为目标,构造如下目标函数:
| ${{f}_{1}}\left( x \right)=\frac{1}{n}\times \sum\limits_{i=1}^{n}{{{a}_{i}}},$ | (2) |
式中:ai为评价点振动加速度的均方根值;n为评价点个数,n=6。
(2.2) 设计变量优化设计选取了12个设计变量,如式(3)所示,各设计变量的含义和取值范围如表 6所示。
| $x=({{h}_{1}},{{h}_{2}},{{h}_{3}},{{r}_{1}},{{r}_{2}},{{r}_{3}},{{b}_{1}},{{b}_{2}},{{b}_{3}},{{b}_{4}},{{b}_{5}},{{b}_{6}})。$ | (3) |
| 表 6 齿轮箱动态响应优化设计变量(mm) Table 6 The design variables of dynamic response optimization of gearbox(mm) |
响应优化过程中设置齿轮箱体积不增加,其状态变量的表达式为
| ${{V}_{sum}}\left( x \right)\le {{V}_{0}},$ | (4) |
式中:Vsum(x)为响应优化迭代中箱体的体积;V0为箱体体积的限制值。
(2.4) 响应优化结果在ANSYS中,利用APDL语言编写命令流程序进行优化求解。优化过程中,目标函数、状态变量和部分设计变量随迭代步的变化曲线如图 7所示,优化求解在第19步收敛,目标函数最小值为10.6 m/s2。优化后箱体的体积为2.683 m3,与优化前箱体体积2.682 m3相比几乎保持不变。表 7给出了优化后设计变量的最优值。

|
图 7 目标函数及优化变量随迭代步数变化曲线 Figure 7 The curve of objective function and optimal variables change with iterative steps |
| 表 7 优化后齿轮箱设计变量的最优值(mm) Table 7 Theoptimal value of optimized design variables of gearbox(mm) |
表 8给出了优化前后增速齿轮箱的振动加速度。由表可知,优化后目标函数最优值为10.6 m/s2,较优化前减少了37.5%,6个评价点处的振动加速度均有较大幅度的减少,优化效果较为显著。
| 表 8 响应优化前后的加速度(m/s2) Table 8 The acceleration of dynamic responsebefore and after optimization(m/s2) |
对增速齿轮箱进行动态响应优化并圆整后,齿轮箱的静强度、固有频率和振动响应都会有所变化,有必要对其进行重新分析,以评价优化效果。
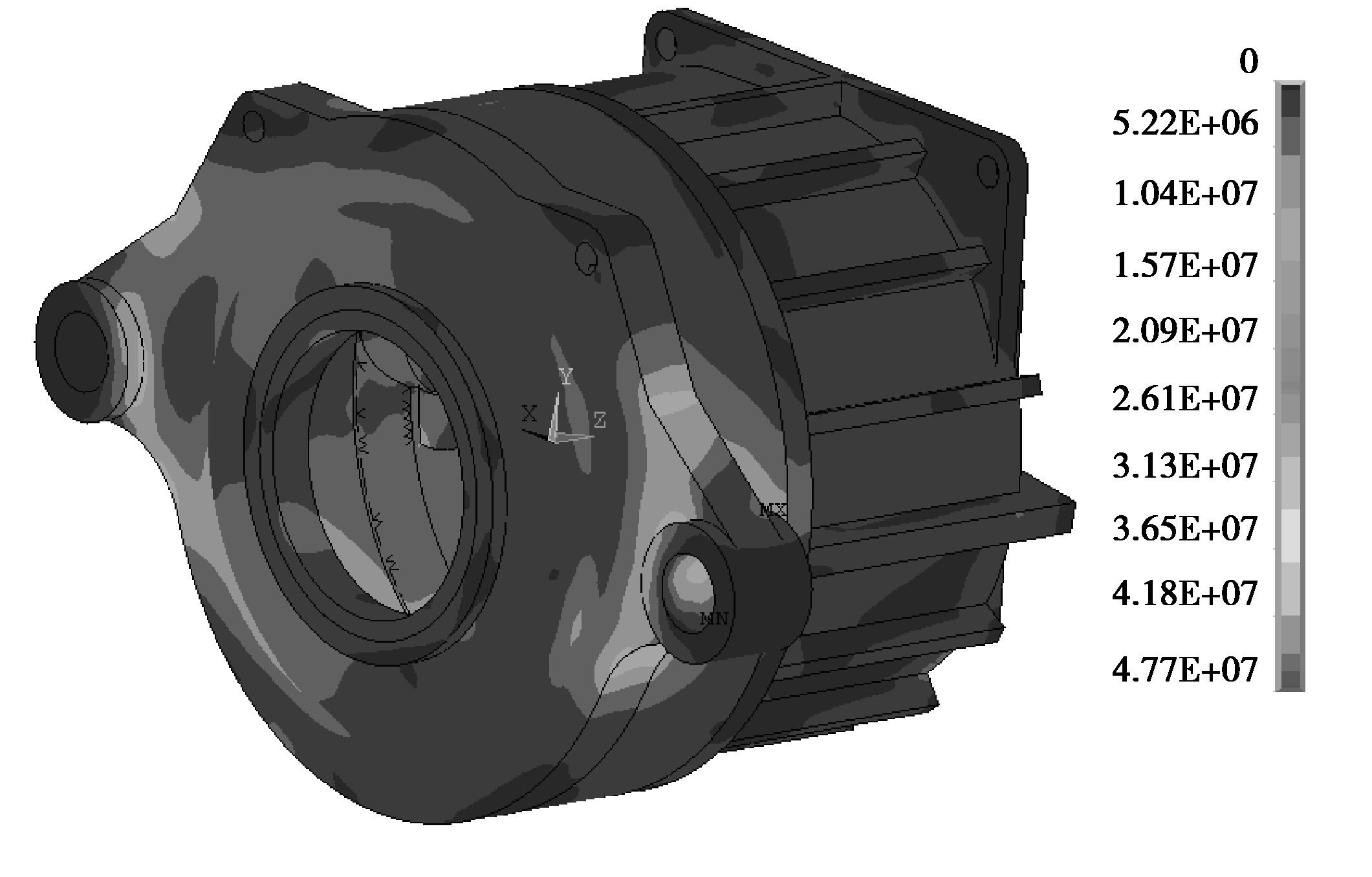
(3.1) 齿轮箱静强度评价建立齿轮箱实体模型,划分网格,施加边界条件,计算可得齿轮箱的等效应力,如图 8所示。齿轮箱优化后等效应力最大值为47.7 MPa,稍大于优化前的46 MPa。箱体材料为QT400-18,屈服强度值为270 MPa,故优化后齿轮箱满足静强度要求。
|
图 8 优化后齿轮箱的等效应力 Figure 8 The equivalent stress of optimized gearbox |
表 9给出了优化后齿轮箱的前8阶固有频率。由表可知,优化前后齿轮箱低阶固有频率相近,这是由于齿轮箱低阶固有频率主要体现为传动系统部分的振动,箱体尺寸参数变化对其影响不大。
| 表 9 优化后齿轮系统前8阶固有频率(Hz) Table 9 The first 8-order natural frequency of optimizedgear system (Hz) |
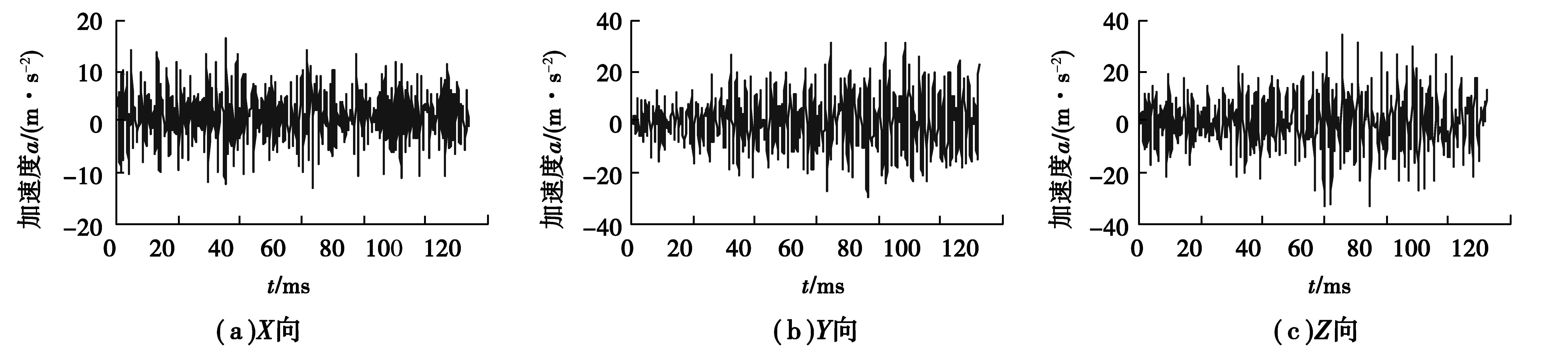
表 10给出了优化并圆整后6个评价点的振动加速度均方根值,各评价点的振动情况较优化前均有所改善,其中评价点129 751振动加速度值为18.71,比优化前的40.68下降了54%,效果最为明显。图 9为响应优化后节点129 751的X、Y、Z 3个方向振动加速度时的域曲线。
| 表 10 优化并圆整后各评价点振动加速度均方根(m/s2) Table 10 The vibration acceleration RMS of evaluation point after optimization and rounding (m/s2) |
|
图 9 节点129751振动加速度时域曲线 Figure 9 The time domain curve of vibration acceleration of node 129751 |
通过风电增速齿轮箱的动力学性能优化分析,得出如下结论:
1) 优化前后增速齿轮箱均不会发生共振,且满足静强度要求。
2) 齿轮箱的频域振动响应峰值出现在齿轮副啮合频率及其倍频附近。
3) 增速齿轮箱动态响应优化后,目标函数减小37.5%,各评价点的振动加速度均有较大幅度的减少,最大值为54%,优化效果较为显著。
| [1] |
邱星辉, 韩勤锴, 褚福磊.
风力机行星齿轮传动系统动力学研究综述[J]. 机械工程学报 , 2014, 50 (11) : 23–36.
QIU Xinghui, HAN Qinkai, CHU Fulei.
Review on dynamic analysis of wind turbine geared transmission systems[J]. Journal of Mechanical Engineering , 2014, 50 (11) : 23–36.
DOI:10.3901/JME.2014.11.023 ( 0) 0)
|
| [2] |
林腾蛟, 廖勇军, 李润方, 等.
齿轮箱动态响应及辐射噪声数值仿真[J]. 重庆大学学报 , 2009, 32 (8) : 892–896.
LIN Tengjiao, LIAO Yongjun, LI Runfang, et al.
Numerical simulation of dynamic response and radiation noise of gearbox[J]. Journal of Chongqing University , 2009, 32 (8) : 892–896.
( 0) 0)
|
| [3] |
Abbes M S, Trigui M, Chaari F, et al.
Dynamic behaviour modelling of a flexible gear system by the elastic foundation theory in presence of defects[J]. European Journal of Mechanics,A/Solids , 2012, 29 (5) : 887–896.
( 0) 0)
|
| [4] |
Lin T J, He Z Y, Geng F Y, et al.
Prediction and experimental study on structure and radiation noise of subway gearbox[J]. Journal of Vibroengineering , 2013, 15 (4) : 1838–1846.
( 0) 0)
|
| [5] |
秦大同, 龙威, 杨军, 等.
变风速运行控制下风电传动系统的动态特性[J]. 机械工程学报 , 2012, 48 (7) : 1–8.
QIN Datong, LONG Wei, YANG Jun, et al.
Dynamic characteristics of wind turbine transmission system under verying wind speed and operation control conditions[J]. Journal of Mechanical Engineering , 2012, 48 (7) : 1–8.
DOI:10.3901/JME.2012.07.001 ( 0) 0)
|
| [6] |
李应刚, 陈天宁, 王小鹏, 等.
外部动态激励作用下齿轮系统非线性动力学特性[J]. 西安交通大学学报 , 2014, 48 (1) : 101–105.
LI Yinggang, CHEN Tianning, WANG Xiaopeng, et al.
Non-linear dynamics of spur gear pair under external periodic excitation[J]. Journal of Xi'an Jiaotong University , 2014, 48 (1) : 101–105.
( 0) 0)
|
| [7] |
Ambarisha V K, Parker R G.
Nonlinear dynamics of planetary gears using analytical and finite element models[J]. Journal of Sound and Vibration , 2007, 302 (3) : 577–595.
DOI:10.1016/j.jsv.2006.11.028 ( 0) 0)
|
| [8] |
Walha L, Fakhfakh T, Haddar M.
Nonlinear dynamics of a two-stage gear system with mesh stiffness fluctuation,bearing flexibility and backlash[J]. Mechanism and Machine Theory , 2009, 44 (5) : 1058–1069.
DOI:10.1016/j.mechmachtheory.2008.05.008 ( 0) 0)
|
| [9] |
Rincon A F D, Viadero F, Iglesias M, et al.
A model for the study of meshing stiffness in spur gear transmissions[J]. Mechanism and Machine Theory , 2013, 61 : 30–58.
( 0) 0)
|
| [10] |
Bozca M.
Torsional vibration model based optimization of gearbox geometric design parameters to reduce rattle noise in an automotive transmission[J]. Mechanism and Machine Theory , 2010, 45 (11) : 1583–1598.
DOI:10.1016/j.mechmachtheory.2010.06.014 ( 0) 0)
|
| [11] |
Faggioni M, Samani F S, Bertacchi G, et al.
Dynamic optimization of spur gears[J]. Mechanism and Machine Theory , 2011, 46 (4) : 544–557.
DOI:10.1016/j.mechmachtheory.2010.11.005 ( 0) 0)
|
| [12] |
张庆伟, 张博, 王建宏, 等.
风力发电机齿轮传动系统的动态优化设计[J]. 重庆大学学报 , 2010, 33 (3) : 30–35.
ZHANG Qingwei, ZHANG Bo, WANG Jianhong, et al.
Dynamic optimization design of gear transmission system for wind turbine[J]. Journal of Chongqing University , 2010, 33 (3) : 30–35.
( 0) 0)
|
| [13] |
秦大同, 古西国, 王建宏, 等.
兆瓦级风力机齿轮传动系统动力学分析与优化[J]. 重庆大学学报 , 2009, 32 (4) : 408–414.
QIN Datong, GU Xiguo, WANG Jianhong, et al.
Dynamic analysis and optimization of gear trains in a megawatt level wind turbine[J]. Journal of Chongqing University , 2009, 32 (4) : 408–414.
( 0) 0)
|
| [14] |
Kim Y I, Park G J.
Nonlinear dynamic response structural optimization using equivalent static loads[J]. Computer Methods in Applied Mechanics and Engineering , 2010, 199 (9-12) : 660–676.
DOI:10.1016/j.cma.2009.10.014 ( 0) 0)
|
| [15] |
魏静, 孙清超, 孙伟, 等.
大型风电齿轮箱系统耦合动态特性研究[J]. 振动与冲击 , 2012, 31 (8) : 16–23.
WEI Jing, SUN Qingchao, SUN Wei, et al.
Dynamical coupling characteristics of a large wind turbine gearbox transmission system[J]. Journal of Vibration and Shock , 2012, 31 (8) : 16–23.
( 0) 0)
|
 2016, Vol. 39
2016, Vol. 39

